线性弯矩分布下的搭接钢筋应力计算方法试验研究

2021-12-24HwangHyeonJong

公路工程 2021年5期

杨帆,马高,Hwang Hyeon Jong,

(1. 湖南大学土木工程学院，湖南长沙 410082；2.韩国建国大学建筑学院，韩国首尔 05029)

0 引言

在钢筋混凝土结构中，钢筋的连接是工程设计和施工中不可避免的问题。常见的钢筋连接方式有搭接连接、焊接连接和机械连接等，其中搭接连接由于其便捷性被广泛使用。在搭接连接中，被搭接钢筋之间的应力通过钢筋与混凝土之间的粘结应力传递，搭接连接实质上是钢筋的粘结锚固问题[1]。

在给定混凝土强度和钢筋屈服强度的情况下，存在一个临界锚固长度，此锚固长度下搭接钢筋达到屈服强度的同时发生粘结失效[2]，此时的搭接钢筋极限应力为钢筋的屈服强度。在此基础上，各学者通过钢筋的搭接对拉试验和搭接混凝土梁试验，为钢筋搭接长度的计算提供了建议[3]。梁业凡[4]通过对49根钢筋混凝土受弯构件的搭接试验研究，建议钢筋的搭接长度按照所选用的钢筋等级和混凝土强度设计等级取搭接钢筋直径的倍数。徐有邻[5]等通过对32个钢筋的搭接对拉试验和8个钢筋搭接梁试验，由可靠度分析给出了基于钢筋基本锚固长度的钢筋搭接长度计算公式，并被我国《混凝土结构设计规范》(GB 50010-2010)[6]所采用。Darwin[7]等通过对133个无箍筋约束钢筋搭接或锚固试件和166个有箍筋约束搭接或锚固试件的试验结果进行分析，得出在钢筋搭接或锚固强度公式中f′c1/4更能体现混凝土强度对钢筋搭接性能的影响，其中f′c为圆柱体抗压强度标准值，并分别给出了搭接钢筋在有箍筋约束和无箍筋约束下的粘结锚固强度计算公式。李艳艳[8]等通过63个棱柱体试件的拉拔试验，研究了600 MPa热轧带肋钢筋的粘结锚固性能，结果表明其锚固性能随混凝土抗拉强度的提高而增大，且在临界混凝土保护层厚度范围内钢筋的粘结锚固性能随着混凝土保护层厚度的增加而提高。

现有的研究主要通过钢筋搭接对拉试验和梁的搭接试验[9]得到钢筋的搭接长度计算公式，进而得到搭接钢筋的钢筋应力计算式。由于搭接梁试验中搭接钢筋处于梁的纯弯曲段，与实际工程中搭接钢筋的受力情况有一定出入，比如地震作用下柱端和梁端的搭接区受到线性弯矩作用，通过现行规范计算得到的线性弯矩分布下的搭接钢筋应力会偏低，造成实际构件的力学性能被低估。此外，按照旧规范设计的既有钢筋混凝土结构存在钢筋搭接长度普遍较短的问题，在对既有结构进行性能评估时，准确计算搭接钢筋应力与结构构件在钢筋搭接区域的承载力是保证结构评估结果可靠的重要基础。针对上述问题，本文提出了一种考虑线性弯矩分布的修正系数，并以GB 50010-2010[6]和ACI 318-19[10]规范公式为例，给出了修正后的搭接钢筋极限应力计算公式，并通过8组搭接钢筋混凝土简支梁的静载试验对公式进行验证。

1 搭接钢筋应力计算公式

1.1 GB 50010-2010计算公式

我国《混凝土结构设计规范》(GB 50010-2010)[6]认为钢筋的搭接长度是与钢筋屈服强度fy、钢筋直径db和混凝土轴心抗拉强度ft相关的函数式，其计算公式如下:

(1)

la=ζalab

(2)

ls=ζlla≥300 mm

(3)

其中,lab为钢筋的基本锚固长度；α为钢筋的外形系数；la为受拉钢筋的锚固长度;ζa为考虑大直径钢筋、钢筋环氧涂层和钢筋保护层厚度等的锚固长度修正系数，由多项修正系数连乘得到，但不应小于0.6；ls为纵向受拉钢筋的搭接长度；ζl为纵向受拉钢筋搭接长度修正系数，根据位于统一连接区段内的钢筋搭接接头面积百分率决定(取值为1.2～1.6)。

在给定搭接长度的条件下，搭接钢筋极限应力fs的计算公式如下:

(4)

1.2 ACI 318-19计算公式

在美国混凝土设计规范ACI 318-19[10]中，钢筋的搭接长度ls取决于钢筋的延伸长度ld，ACI 318-19将钢筋的搭接接头分为A级和B级两类，当搭接钢筋的面积大于计算所需面积的2倍，且搭接长度范围内的搭接接头百分比为50%或更小时定义为A级搭接，其余情况下为B级搭接。对于A级搭接，钢筋搭接长度ls=1.0ld；对于B级搭接，钢筋搭接长度ls=1.3ld。钢筋的延伸长度ld计算公式如下:

cf=min(cb，cso，csi)+0.5db

(5)

Ktr=40Atr/(stn)

(6)

(7)

其中,λ为混凝土类别系数，取值为0.75～1.0；ψt、ψe、ψs分别为新拌混凝土系数、钢筋环氧涂层系数和钢筋直径系数；cb、cso、csi分别为搭接钢筋表面与混凝土表面的最小竖向间距、与混凝土表面的最小横向间距和到其他纵筋表面的间距；Atr为箍筋间距st内横跨潜在开裂面的所有横向钢筋的截面积之和；n为沿着开裂所搭接或锚固的钢筋的数量。考虑到钢筋的拔出破坏，(cf+Ktr)/db的限值为不大于2.5。

在给定搭接长度的条件下，搭接钢筋极限应力fs的计算公式如下:

(8)

(9)

其中,式(8)为A级搭接钢筋的应力计算公式，式(9)为B级搭接钢筋的应力计算公式。

1.3 钢筋搭接长度的线性弯矩分布系数

在一般的钢筋混凝土梁四点加载搭接试验中，搭接钢筋长度范围处于试验梁的纯弯曲段，而在实际工程中搭接钢筋区域通常受弯矩和剪力同时作用，钢筋搭接长度范围内受线性弯矩分布作用，搭接钢筋受到的总拉力降低，因此对于钢筋的粘结强度要求也随之下降[11]。本文提出了一种弯矩分布系数对给定搭接长度下钢筋应力的计算公式进行修正，其基本假定如下：

a.在搭接钢筋达到其屈服强度之前，钢筋的应力与对应截面所受弯矩值为线性关系。

b.钢筋搭接长度范围内没有集中荷载作用。

在线性分布的弯矩区域中，钢筋搭接接头的粘结应力需求可以定义为fmax和fmin之间的平均拉应力fs0(其中fmax和fmin是分别对应于钢筋搭接长度内的最大弯矩Mmax和最小弯矩Mmin截面的搭接钢筋最大、最小应力)。则fs 0可以定义为：

(10)

图1为实际试件的理想化模型与弯矩分布情况，其中a为到钢筋搭接长度端部的剪跨长度，则式(10)可以进一步变为：

(11)

图1 搭接钢筋线性弯矩分布 Figure 1 Linear moment distribution on lap splices

定义线性弯矩分布系数αs=2a/(2a-ls)，当搭接钢筋受纯弯矩作用时取值为1.0。则在给定钢筋搭接长度下计算搭接钢筋极限应力时，可以得到修正钢筋应力计算公式：

(12)

其中,fs为现有规范中计算得到的钢筋应力结果，将式(4)、式(8)和式(9)分别代入，得到修正后的GB 50010-2010和ACI 318-19搭接钢筋应力计算公式分别如下：

(13)

(14)

(15)

式中:ls取实际钢筋搭接长度。式(13)为修正后的GB50010-2010搭接钢筋应力计算公式，式(14)和式(15)分别为修正后的ACI 318-19对于A级搭接和B级搭接的钢筋应力计算公式。

2 试验概况

2.1 试件设计

设计制作了8根搭接钢筋混凝土梁，试验的主要参数为钢筋搭接段的弯矩分布、搭接纵筋直径以及搭接段的配箍率，试验梁的截面尺寸均为450 mm×450 mm。对其中4个试验梁进行四点加载试验，四点加载试验梁的长度为4 000 mm，净跨为3 500 mm；对其余4个试验梁进行三点加载试验，三点加载试验梁的长度为2 500 mm，净跨为2 000 mm；混凝土设计强度为C35级，搭接钢筋采用强度等级为HRB400、直径分别为18 mm和25 mm的带肋钢筋；箍筋采用强度等级为HRB400、直径为8 mm的带肋钢筋，除支座截面附近和部分试验梁在搭接钢筋长度范围内没有配置箍筋外，箍筋的间距均为200 mm；钢筋搭接长度均为300 mm，两根纵向钢筋于试验梁跨中同一截面处搭接连接，搭接接头百分比为100%。试验梁的尺寸及配筋、搭接构造见图2。当钢筋搭接长度范围内有箍筋约束时，搭接长度300 mm内设有两道箍筋，间距为200 mm，即两侧箍筋离搭接长度边缘的距离均为50 mm。

图2 试验梁配筋及搭接钢筋详图 (单位: mm)Figure 2 Detail of test beam reinforcement and lap splices (Unit: mm)

试验梁编号及主要参数见表1。编号中L和D分别表示四点搭接试验梁和三点搭接试验梁，R及之后的数字表示搭接钢筋直径，S表示钢筋搭接长度范围内配置了间距为200 mm的箍筋。

表1 试验梁主要参数和混凝土抗压强度值Table 1 Main parameters and concrete compressive strength of test beams试件编号净跨长度L0/mm截面尺寸b×h/mm×mm钢筋直径db/mm钢筋搭接长度ls/mm箍筋间距/mm剪跨长度a/mm线性弯矩分布系数αs立方体抗压强度fcu/MPaL1-R18S3 500450×45018300200—1.0036.1L2-R183 500450×45018300——1.0031.6L3-R25S3 500450×45025300200—1.0031.0L4-R253 500450×45025300——1.0030.7D1-R18S2 000450×450183002001 0000.8532.6D2-R182 000450×45018300—1 0000.8535.3D3-R25S2 000450×450253002001 0000.8531.3D4-R252 000450×45025300—1 0000.8533.7

2.2 试验材料

采用设计强度为C35等级的普通混凝土，每个试验梁在浇筑时均预留3个150 mm×150 mm×150 mm 的混凝土立方体试块，与试验梁在同等条件下养护。采用标准试验方法测得混凝土的力学性能，试验梁同期立方体抗压强度fcu见表1。钢筋强度等级均为HRB400级，纵向受力钢筋直径为18 mm 和25 mm，箍筋直径为8 mm，实测钢筋力学性能见表2。

表2 钢筋力学性能Table 2 Mechanical properties of rebar钢筋类别屈服强度fy /MPa极限强度fu /MPa钢筋伸长率δ / %HRB400 C850663022.7HRB400 C1848060816.7HRB400 C2546058229.4

2.3 加载装置及加载制度

试验采用静力加载试验方法，试验梁浇筑完成并在标准条件下养护28 d后，进行四点弯曲加载试验或三点加载试验，试验装置如图3所示。利用压力传感器读取荷载数值，并由梁跨中截面下方及两端支座截面上方的电子位移计来量测跨中挠度值及两端支座沉降值。

(a)四点加载试验

试验采用荷载控制加载制度，先通过一次预加载检查试验装置与仪器、仪表的可靠性并进行校正后卸载清零。之后在正式试验阶段采用分级加载，每级加载值为预估承载力的5%，每级荷载持续时间为5 min。在荷载持续时，记录每个试件的裂缝开展情况。由于钢筋搭接长度有限，试验期间钢筋可能达不到屈服强度，加载至荷载不再上升，且荷载值回落到低于峰值荷载的85%后停止试验。

3 试验结果

3.1 破坏过程

各试验梁的破坏形态均为搭接钢筋的粘结锚固失效，随着荷载的增加，第一条裂缝出现在试验梁的跨中部位，试件梁开裂后裂缝在钢筋搭接区域附近迅速发展，破坏时搭接钢筋附近的混凝土同时产生垂直于钢筋长度方向和平行于钢筋长度方向的裂缝(见图4)，搭接钢筋发生粘结锚固失效，试验梁失去承载力。对于所有试验梁，破坏时试验梁承受的最大剪力值均远低于计算抗剪强度，未发生剪切破坏，试验梁的裂缝分布情况见图5。

图4 试验梁底部的裂缝分布Figure 4 Splitting cracks on the bottom of the test beams

(a)L1-R18S

各试验梁的荷载-跨中位移曲线如图6所示，在达到开裂荷载前，荷载与试验梁的跨中位移基本为线性关系。达到开裂荷载后，试验梁的跨中挠度开始迅速增长。

(a)L1-R18S

3.2 试验结果分析

以试验梁在承受极限荷载时其最大弯矩截面处的弯矩值作为试验梁的极限抗弯承载力，本文引入修正Kent&Park混凝土应力-应变模型[12]和钢筋的弹塑性模型，将试验梁的设计参数和实测材料强度代入计算得到各试验梁的弯矩-曲率关系，通过截面分析法得到试验梁截面在极限弯矩下对应的钢筋应力值fs，各试验梁的试验结果如表3所示。

表3 试验结果Table 3 Test results试件编号极限荷载Pu/ kN极限抗弯承载力Mu/ MPa钢筋应力fs/ MPaL1-R18S98.559.3306.1L2-R18103.562.2321.7L3-R25S136.481.8226.1L4-R2590.354.2150.0D1-R18S143.171.5369.3D2-R18146.473.0376.3D3-R25S197.198.9274.1D4-R25142.171.1196.5

由表3可见，由于采用了较短的搭接长度，各试验梁中的搭接钢筋应力均未达到其材料屈服强度，在搭接钢筋屈服前试验梁就因为钢筋的粘结锚固失效而失去了承载力，各试验梁的极限抗弯承载力均由钢筋的搭接性能控制。

相较于四点加载试验梁，在其余试验参数相同的情况下三点加载试验梁普遍有更高的抗弯承载力。采用三点加载方式的试验梁其抗弯承载力平均提高了22.5%。从试验结果还可以看出箍筋约束对于直径为18 mm的钢筋的搭接性能提升不明显，但对于直径为25 mm的搭接钢筋，与搭接钢筋长度范围内没有配置箍筋的情况相比，钢筋搭接区域配置有箍筋的试验梁抗弯承载力提高了45.0%。

试验梁的钢筋搭接百分比为100%，对于ACI 318-19规范来说属于B级搭接。将试验梁的设计参数和实测材料强度带入式(4)和式(9)，取试验梁实际钢筋搭接长度ls=300 mm，计算得到GB 50010-2010和ACI 318-19对试验梁钢筋极限应力的计算值值，同时使用弯矩分布修正后的钢筋应力计算公式(13)和式(15)对钢筋的理论应力值进行计算，并与实际试验结果进行对比，结果如表4所示。计算中参考GB 50010-2010对混凝土强度进行换算，换算公式下:

f′c=0.8fcu

(14)

(15)

定义γmod为试验梁钢筋应力值fs与各规范钢筋应力预测值fcal的比值。由表4可见，GB 50010-2010和ACI 318-19公式对于试验梁的搭接钢筋极限应力的计算结果都偏于安全。对于GB50010-2010，在进行线性弯矩分布修正前，γmod的平均值为1.59，在引入线性弯矩分布系数进行修正后，γmod的平均值为1.46。对于ACI 318-19，在进行线性弯矩修正前，γmod的平均值为1.79，在引入线性弯矩分布系数进行修正后，γmod的平均值为1.65。在进行弯矩分布系数修正后整体预测结果的离散程度降低，对GB 50010-2010，修正后预测结果的变异系数从0.170降低至0.146，对ACI 318-19，修正后预测结果的变异系数从0.185降低至0.160。

表4 理论计算与试验结果对比Table 4 Comparison between calculated results and test results试件编号钢筋应力fs/MPaGB 50010-2010 (修正前)GB 50010-2010 (修正后)ACI 318-19(修正前)ACI 318-19(修正后)fcal/MPaγmodfcal/MPaγmodfcal/MPaγmodfcal/MPaγmodL1-R18S306.1211.31.45211.31.45236.81.29236.81.29L2-R18321.7196.31.64196.31.64206.51.56206.51.56L3-R25S226.1139.91.62139.91.62112.32.01112.32.01L4-R25150.0139.11.08139.11.0891.61.6491.61.64D1-R18S369.3199.71.85234.91.57225.11.64264.81.39D2-R18376.3208.71.80245.51.53218.31.72256.81.47D3-R25S274.1140.61.95165.41.66112.82.43132.72.07D4-R25196.5146.51.34172.41.14962.05112.91.74平均值1.591.461.791.65变异系数0.1700.1460.1850.160注: fcal为计算得到的钢筋极限强度预测值,γmod=fs/fcal。

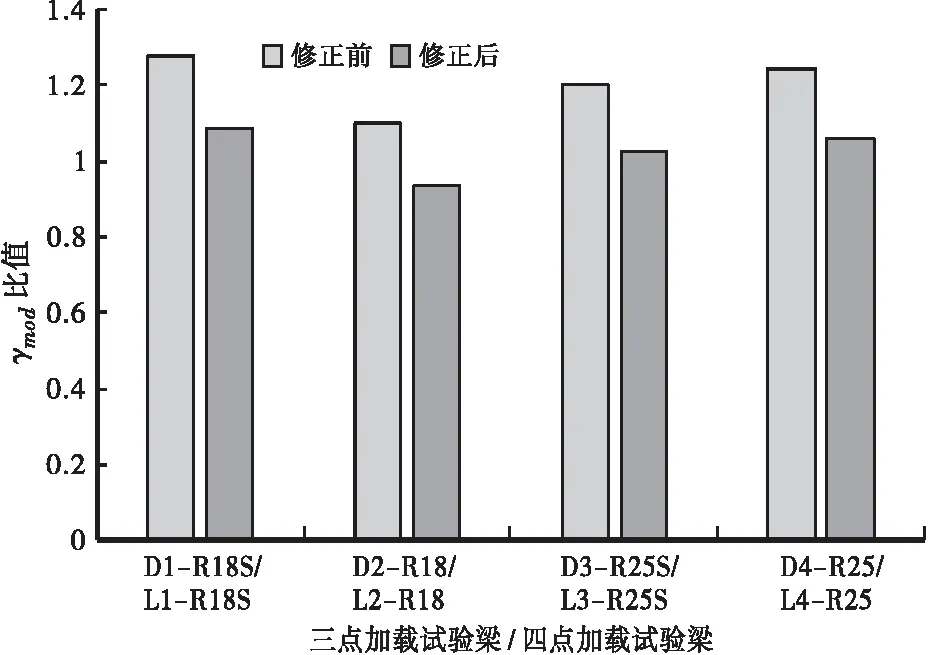
图7比较了配筋情况条件相同的三点加载试验梁和四点加载试验梁的γmod比值，由图7可以看出，修正后的预测值更加符合试验实际情况，在修正前，各规范公式未考虑弯矩分布的影响，对三点加载试验梁的预测值普遍偏低，考虑线性弯矩分布系数后，各规范对于三点加载试验梁和四点加载试验梁的预测比较接近。修正前GB 50010-2010和ACI 318-19中三点加载试验梁与四点加载试验梁的γmod平均比值分别为1.20和1.21，修正后降低至1.02和1.03，即修正后的各规范公式对于纯弯矩和线性弯矩分布作用下的搭接钢筋应力具有相同水平的预测能力。