山区地形改正密度逐次回归选取方法

高维强，史朝洋，张利明，冯旭亮

(1.陕西省矿产地质调查中心，陕西 西安 710068；2.西安石油大学 地球科学与工程学院，陕西 西安 710065)

0 引言

实测重力数据经过高度校正、纬度校正、地形校正和中间层校正，即可得到布格重力异常，其为重力资料解释的基础。然而，对于地形变化较大的山区，布格重力异常往往与地形高程呈镜像或同像变化，即山形异常[1-2]，给地质构造解释推断带来极大的困难。

引起山形异常的主要原因为地形和中间层改正时中间层密度不准确[3]，可利用实测重力数据与高程散点图拟合的中间层校正系数C=2πGσ反算中间层密度[2,4]。但地形起伏较大的山区，其地形物质规模缩小，所产生的重力效应小于布格板重力效应，据此反算的中间层密度偏小[1]。Thorarinsson and Magnusson[5]将分形分析引入重力勘探领域，在冰岛西南部取得了良好的地质效果，但该技术必须对复杂地表按同一密度层分区，区内岩石密度越单一，该方法的效果越好[6]，因此实际应用中较难做到[7]。

相关分析法是选取最佳中间层密度的传统方法，一般在重力剖面上选用一系列中间层密度值进行校正，选用与地形无关或最小相关的布格重力异常值对应的密度值作为最佳中间层密度[8-9]。在同一测区，如果表层密度较为均匀，则图解剖面法是有效的[10]，否则图解法所求密度只是剖面位置处的合适密度，不能代表整个测区密度[10-11]，可对全区地改后的布格重力异常与地形高程进行相关分析，选取相关性最小的地层密度作为最佳地改密度[11]。当地表密度横向变化较大时，可分区选用最佳密度值并拼接形成全区变化的中间层密度[12]，也可在常密度改正结果的基础上进行补偿校正[13-15]。然而，当研究区面积较大且需要分区计算时，计算量较大，并且只能得到与最佳中间层密度最为接近的密度而并非最“真实”的密度。

蔡尚中[2]建立了自由空间重力异常与高程之间的函数关系，之后根据每个测点实际高程计算出回归异常并从实测自由空间重力异常中消除，得到回归剩余异常，有利于定性解释。当研究区较大时，可采用滑动窗口回归分析方法，并可利用变差函数给出窗口大小选取的量化参考值[16]。然而，回归分析方法仅考虑了研究区范围之内地形和重力异常的关系，得到的回归重力值仅为与地形起伏呈整体区域性变化的重力异常，并不能消除局部异常(特别是研究区以外地形的重力影响)，此外，该方法消除的区域异常中可能包含了深部地质信息引起的有用的重力异常。

若有研究区地表地质露头实测的岩石密度，可采用插值和圆滑方法构建地表密度分布模型，并建立浮动基准面进行地形和中间层校正[7]。然而当研究区面积较大时，有限的露头采样和钻井测量资料并不能全面反映测区地表岩石密度的变化情况。牛源源等[17]针对这一问题，从一维自由空气重力异常数据出发，采用贝叶斯方法估算近地表岩石密度，其与地表地质及区域地层密度资料较为吻合，但目前仅用于剖面重力异常分析，并未见到面积性重力异常的相关应用。

重力数据同时包含了构造和密度信息，已有研究表明利用重力数据可以较准确地估算近地表岩石密度[17]或密度界面上下的密度差[18]。Florio[19-20]进行沉积盆地基底深度重力反演时，根据回归分析获得盆地沉积层与基底的密度差，经过几次迭代便可获得满意的结果。受这一思路的启发，本文在处理唐昭陵所在的九嵕山地区的高精度重力资料时，利用逐次回归技术分析最佳地改密度，将其应用于重力资料外部校正之中，取得了较好的应用效果。

1 研究区概况

九嵕山位于鄂尔多斯盆地南缘，西邻祁连—河西走廊(六盘山)—贺兰山构造带，南隔渭河地堑与秦岭造山带相依，地处稳定的鄂尔多斯地块与活动的祁连—秦岭造山带之间(图1)，具有长期复杂的地质构造背景。研究区一带位于鄂尔多斯南缘翘起带，为一强烈的近东西向褶皱带，总体构造形态为一复背斜。次级背、向斜东西成带状展布，褶皱紧密，局部向南倒转，两翼断层多见。唐王陵向斜槽部为上奥陶统唐王陵组，南翼向北倾，350°-10°∠20°-30°，北翼向南倾，倾角较陡，一般产状为170°-190°∠50°-60°。由于北翼北断层破坏，地层出露不全，总体为一不对称向斜。

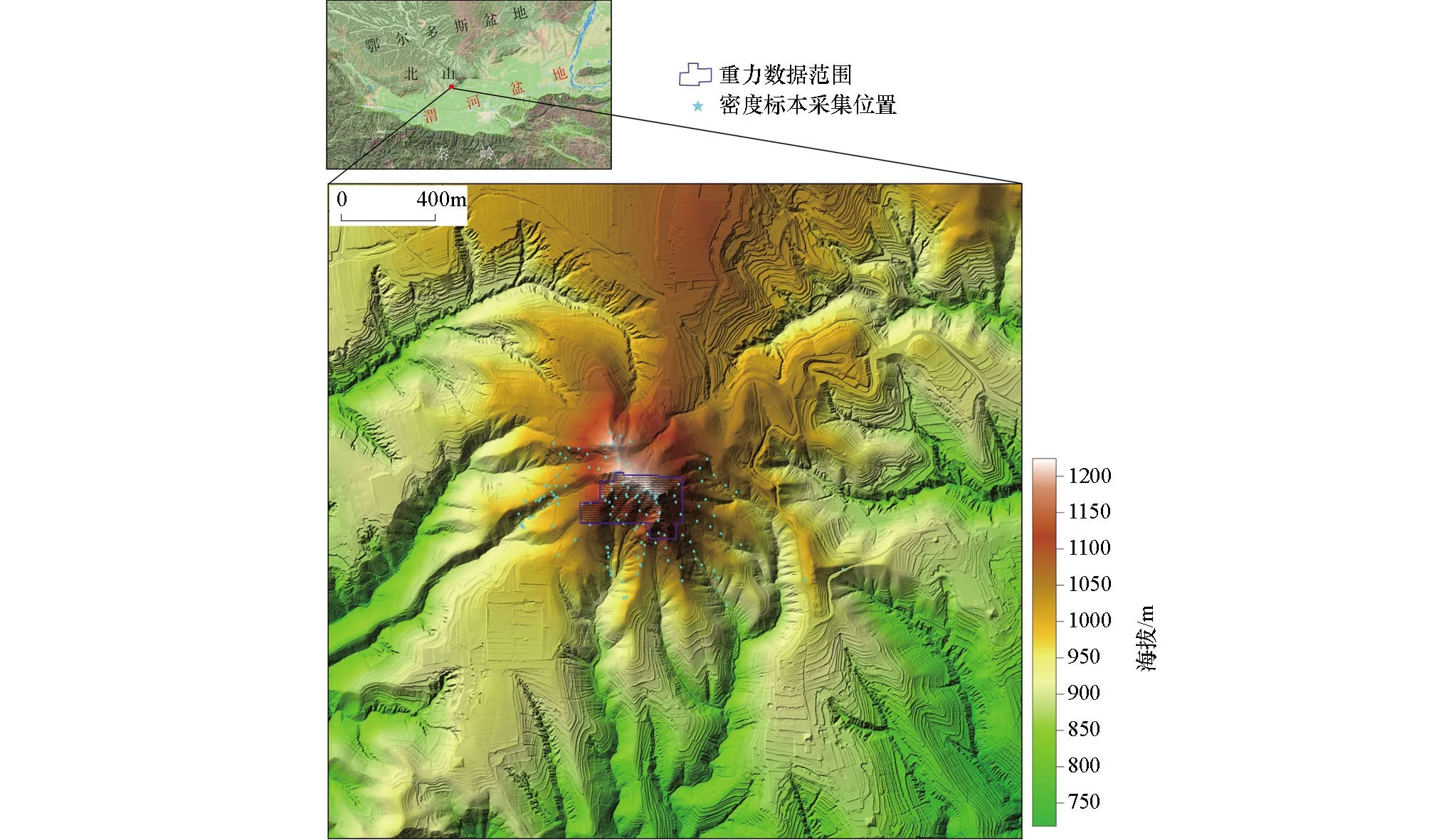
图1 九嵕山及邻区无人机激光雷达测量的地形

研究区位于唐王陵向斜的南翼，主要出露奥陶系唐王陵组，按岩性可分为两段：下段(O3t1)为杂色(黄褐、灰绿、紫红、深灰)含砾页岩，底部夹厚层状岩屑砂岩，并发育燧石条带白云岩大漂砾；上段(O3t2)为灰色、浅灰色巨厚层状复成分砾岩、角砾岩，偶夹砾屑砂岩，上下两段间为整合接触。

2 地球物理特征

研究区共进行了1 722个点的重力测量，其中线距为10 m，点距为5 m。对原始重力测量值进行高度校正和正常场校正，得到自由空间重力异常如图2所示，其与地形(图3)呈明显的同相变化关系，在不到200 m的海拔高度变化范围内，重力异常的局部变化接近10×10-5m/s2。

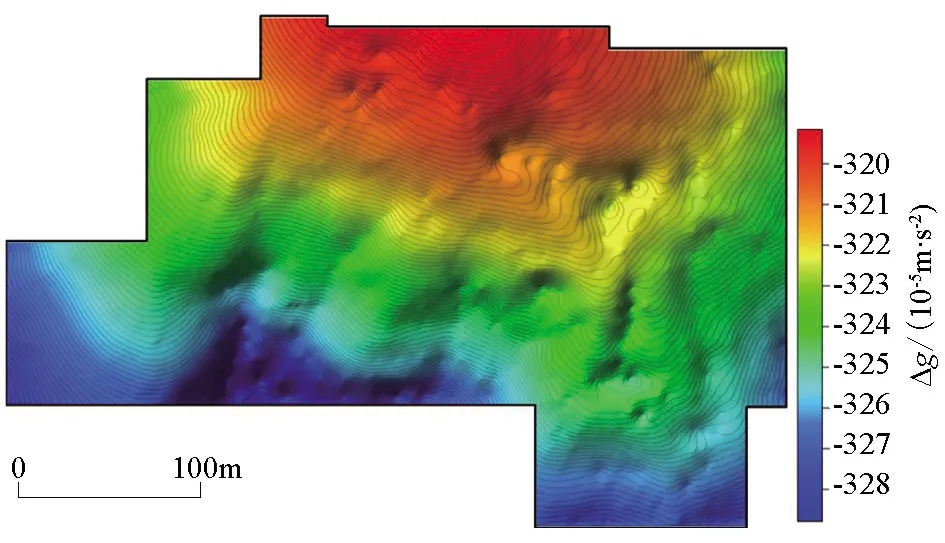
图2 研究区自由空间重力异常

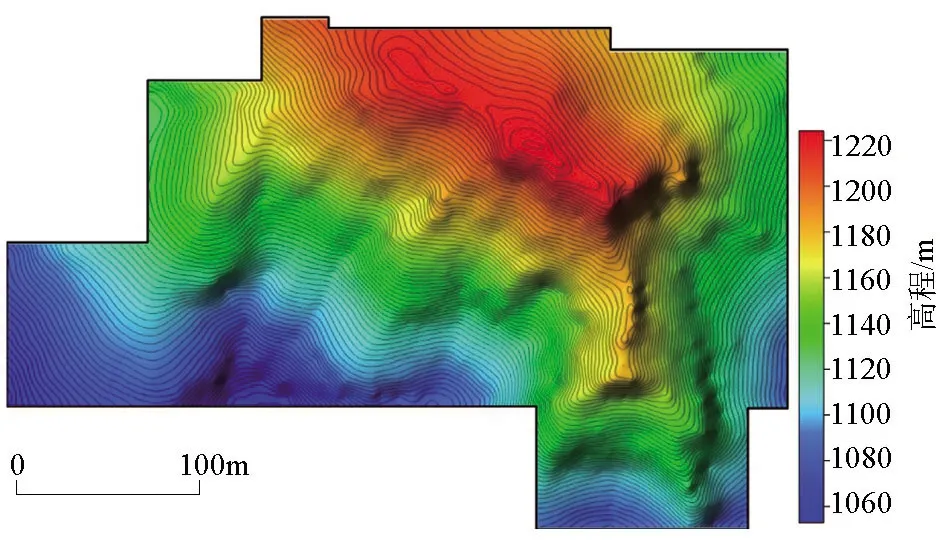
图3 研究区地形

研究区大面积出露奥陶系唐王陵组，第四系非常薄，且仅分布于局部地区，最大厚度不超过1 m。未获得研究区地形改正密度，在研究区不同位置实测了156块标本的密度(位置如图1中蓝色五角星所示)，统计结果见表1，对于标本数量较少的岩性，仅给出平均密度。研究区各类岩石密度整体较大，大多数岩石密度为2.7×103kg/m3左右，砂砾岩和杂色砾岩的密度超过了2.77×103kg/m3。可见，尽管研究区主要出露奥陶系唐王陵组，但由于地层岩性变化较大，使得地层密度也并非统一的密度，且具有较为明显的变化。

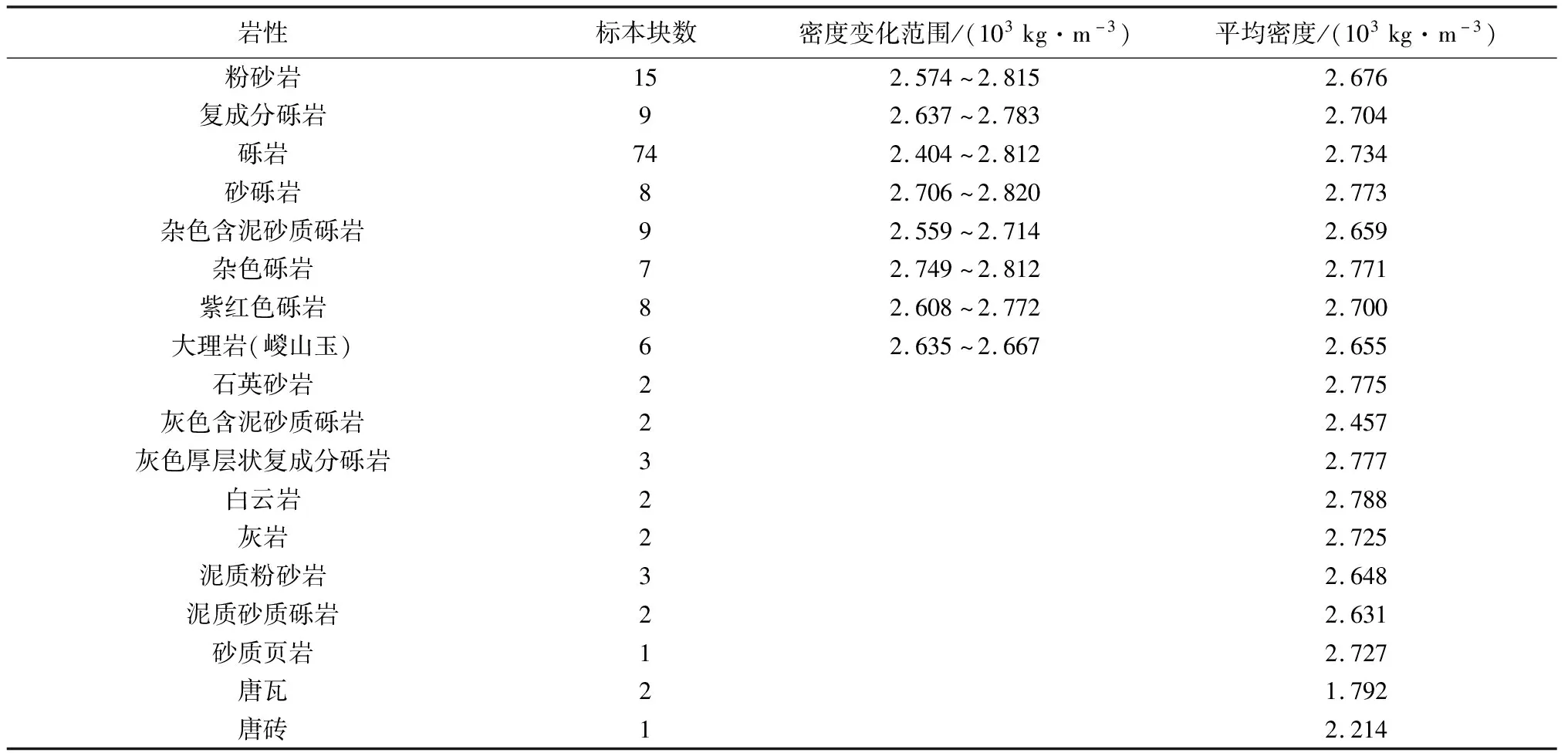
表1 研究区各类岩石密度统计

3 常规地形改正结果

严良俊等[7]根据实测的地表密度资料建立横向的密度变化并用于地形校正，取得较好的地质效果。根据此方法，本文对除唐瓦和唐砖之外实测的153个点上的岩石密度值进行网格化以建立表层变密度模型用于地形校正。为避免密度不连续引起的布格重力异常的畸变，对原始密度网格数据进行光滑，并根据地表地质资料对实测密度外围的岩石密度进行推断补充及扩边，最终形成与图1所示的地形范围一致的地表横向变密度数据，作为地形改正的依据。

自由空间重力异常经地形改正和中间层改正之后可得到布格重力异常。传统的做法是先将任一测点周围的地形“削平补齐”，然后利用布格板公式计算各测点与基点之间的无限大物质层的重力影响，即先做地形改正，再做中间层改正。在计算测点的地形改正值时，先计算测点附近4个节点的地形改正值，然后将4个节点的地形改正值内插到测点位置上来作为测点的地形改正值[21]。本文在进行地形改正时，根据实测的地形起伏直接计算地形在研究区各重力测点引起的重力变化，并从自由空间重力值中消除，得到布格重力异常。这一过程相当于将传统的地形改正和中间层改正合并为一项进行，简化了计算过程，并且避免了地形改正值内插的误差。因此，如不特别说明，本文中的地形改正均指的是传统的地形改正和中间层改正之和。

如果重力测量仅用于研究范围较小的局部异常，地形校正范围可以采用最大半径为20 km进行校正，把远区地形校正当做区域异常将其消除即可[22]。九嵕山研究区重力测量的目的是推断昭陵墓道位置及墓室结构，其为局部浅地表目标体。因此，本文仅计算了图1所示范围内地形的影响而忽略了该区外围地形的影响。计算地形影响时选择最低测点所在的位置为基点位置，并考虑测点之外地形的整体变化趋势，最终选择1 000 m为基点所在平面，正演计算实测地形表面与该平面之间的物质在各测点所引起的重力异常，如图4a所示，从自由空间重力异常中消除地形影响，得到布格重力异常如图4b所示。

图4b所示的布格重力异常与地形呈镜像关系，即呈明显的山形异常，二者之间相关系数为-0.989，可见布格重力异常受地形的影响非常严重。从图4a来看，地形影响值变化形态与自由空间重力异常形态非常相似，二者的相关系数为0.996，但前者相对变化明显大于后者，其原因为利用实测数据建立的地形改正密度偏大。通过野外踏勘也发现，研究区地表岩石风化比较严重，导致岩石的实际等效密度远小于实测密度。图5为不同测点处地表岩石露头照片，可以看出岩石裂隙非常发育且不同位置裂隙规模差异较大，并且裂隙在纵向上延伸范围也比较大。此外，部分裂隙中充填了黄土，部分裂隙中无充填物。研究区各类岩石裂隙规模的变化及充填物的变化导致最佳地形改正密度无法利用实测岩石密度及裂隙的发育程度去估计，只能采用间接的方法，即根据实际地形与重力异常的关系进行估计。

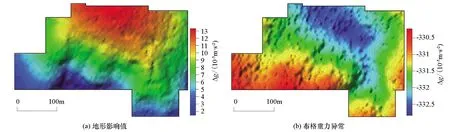
图4 研究区由实测密度计算的地形影响值及相应的布格重力异常

图5 研究区部分测点处地表露头俯视(a～e)和远景(f)照片

4 逐次回归地形改正密度选取方法及应用

在地形起伏较大的山区利用实测重力数据与高程散点图拟合的中间层校正系数，进而根据布格板公式反算的地形改正密度偏小[1]，可对该密度进行迭代调整而得到最佳地改密度。利用重力资料反演密度界面深度时，常利用布格板重力公式构建密度界面深度修改量的迭代计算公式，并逐次迭代消除剩余重力异常值则可反演得到密度界面深度[23-24]。受迭代法的思想启发，本文在选取最佳地形改正密度时采用以下步骤：

1)根据自由空间重力异常与高程的散点图，利用公式进行拟合，并计算第一次地形改正密度σ(1)=a/(1.6πG)，其中G为万有引力常量。需要说明的是，由于三维条件下，实际地形引起的重力变化小于相同密度时布格板的重力异常，因此本文将布格板公式中的系数2πG改为1.6πG以加速迭代收敛过程。

2)以σ(1)为地形改正密度，正演计算地形在测点处的重力影响值gt(1)，并根据gB(1)=gf-gt(1)计算布格重力异常。根据自由空间重力异常与第一次计算的地形在测点处的重力影响值的散点图，利用公式gf=c·gt(1)+d进行拟合，并根据系数c的大小判断：当c明显大于1时，说明计算的地形影响值偏小，地形改正密度σ(1)偏小，继续下一步骤；当c明显小于1时，说明计算的地形影响值偏大，地形改正密度σ(1)偏大，继续下一步骤；当c≈1时，说明地改密度σ(1)取值合适，此时停止迭代，将布格重力异常作为最终结果。

3)根据第一次计算得到的布格重力异常与高程的散点图，利用公式gB(1)=e·h+f进行拟合，计算第一次地形改正密度修正值δ(1)=e/(1.6πG)。

4)根据σ(2)=σ(1)+δσ(1)计算第二次地形改正密度，并令σ(1)=σ(2)转回步骤2)。

根据以上步骤，本文计算了九嵕山地区布格重力异常。研究区自由空间重力异常与测点高程的散点图及拟合公式如图6所示。由拟合一次项系数得到第一次地改密度值σ(1)=1.489×103kg/m3，据此计算得到地形重力影响值及相应的布格重力异常如图7a、b所示。此时自由空间重力异常与图7a所示的地形影响的散点图(图8)中，线性拟合的一次项系数为1.4843，其明显大于1，说明计算的地形影响值偏小。根据布格重力异常与高程的散点图(图9)，由拟合一次项系数得到第一次地形改正的修正值δ(1)=0.463×103kg/m3，则第二次的地形改正密度σ(2)=1.952×103kg/m3。

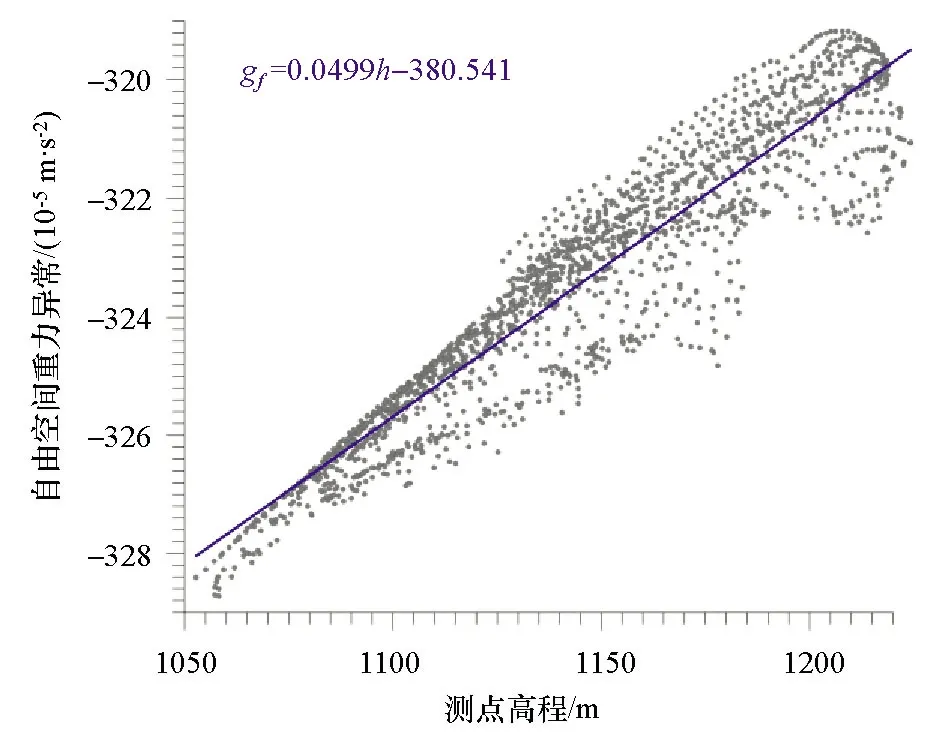
图6 研究区自由空间重力异常与高程散点

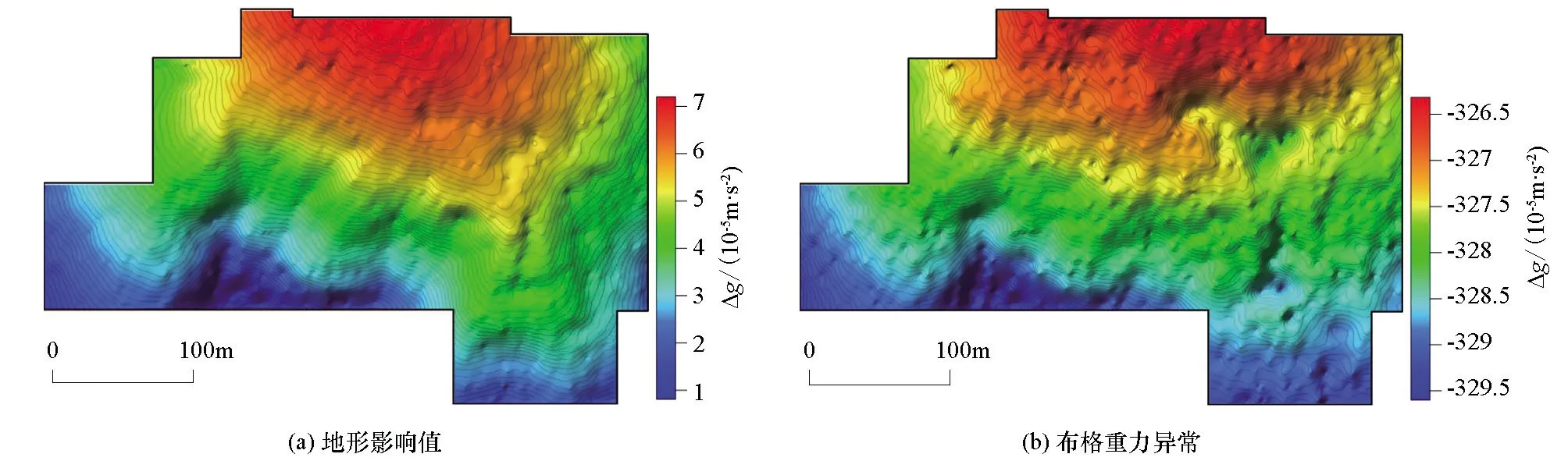
图7 研究区由第一次回归密度计算的地形影响值及相应的布格重力异常

图8 研究区自由空间重力异常与第一次计算的地形影响值散点

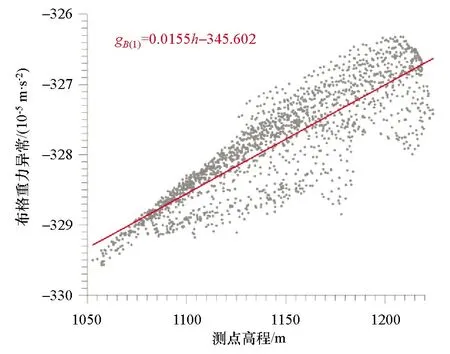
图9 研究区第一次计算的布格重力异常与高程散点

利用此方法，经过5次迭代，得到最佳地形改正密度σ(5)=2.154×103kg/m3。地改密度随迭代次数的变化如图10a所示，自由空间重力异常与计算的地形在测点处的重力影响值的相关系数c随迭代次数的变化如图10b所示。迭代初始，密度随迭代次数变化较大，随着迭代次数增加，密度值变化不明显，相关系数c也逐渐趋于1，证明此事已经得到了最佳密度，再增加迭代次数意义不大。

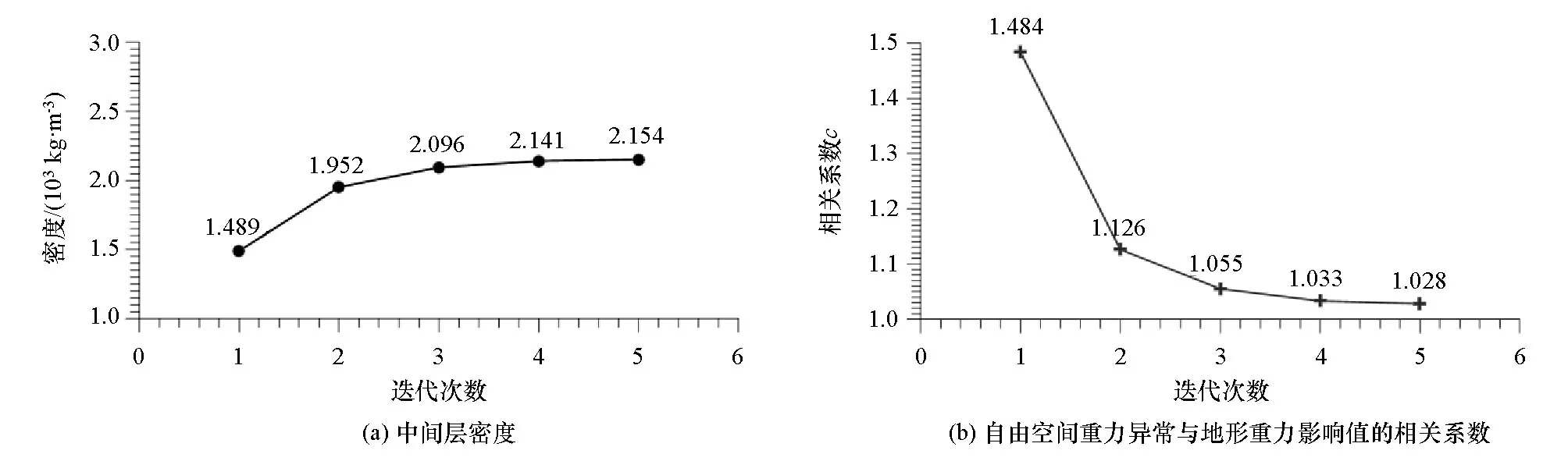
图10 密度及相关系数随迭代次数的变化

假设研究区地表岩石平均密度为2.7×103kg/m3，则该最佳密度值近似于未风化岩石密度的80%，从地表岩石露头的裂隙发育来看，估算裂隙度10%～30%，考虑裂隙中存在部分黄土充填，因此本文估算的最佳地形改正密度应该是合理的。根据该密度计算的布格重力异常如图11a所示，其与地形的相关系数仅为0.0329，可见布格重力异常与地形完全无关。

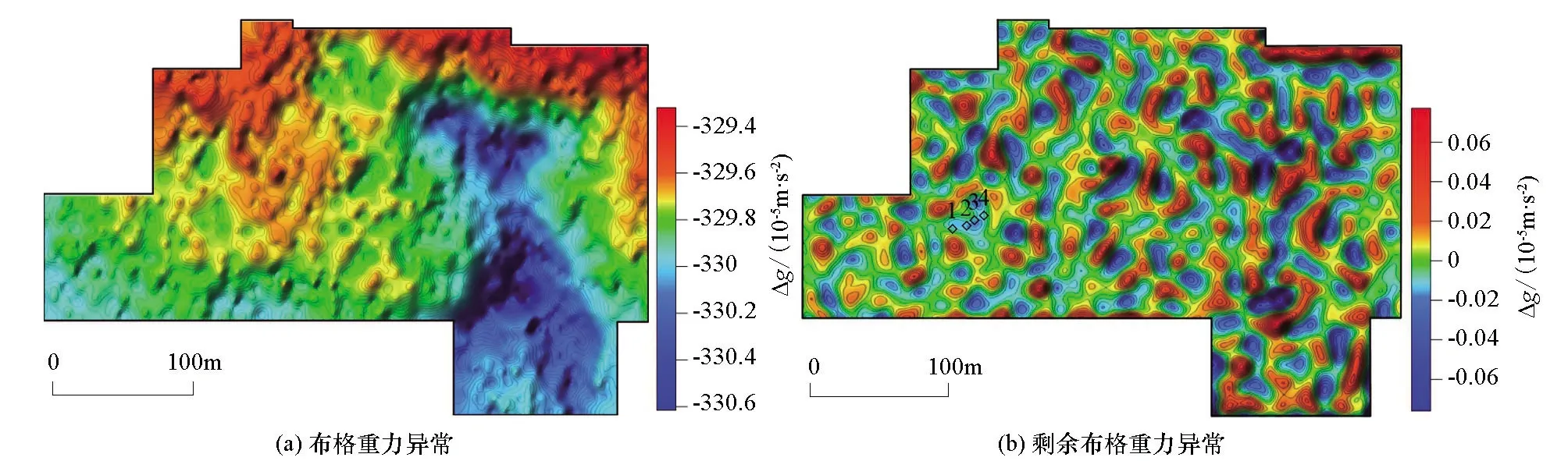
图11 研究区布格重力异常

研究区有4个大小不等的石硐(位置如图11中黑色方框所示)，尺寸约为4 m(宽)×3 m(高)×5.5 m(深)，石硐顶距地表约8～10 m。若按照上述估算的中间层平均密度，则石硐与围岩的密度差为-2.154×103kg/m3，正演计算4个石硐引起的重力异常，其为局部重力异常低，最大幅值可达-0.046×10-5m/s2。利用位场分离方法求取剩余布格重力异常如图11b所示，4个石硐处表现为明显的局部重力异常低，相同参数下对图4b所示的布格重力异常求取的剩余异常则无法反映石硐的重力异常特征，且剩余重力异常走向与地形呈明显相关关系。可见，本文利用逐次回归方法得到的中间层密度较为合理，能较好地消除与地形无关的虚假异常。

5 讨论

本文根据自由空间重力异常与地形的相关关系，利用逐次回归方法确定了山区地形改正的密度，九嵕山地区的实测重力异常校正结果说明该方法的正确性。对于山区重力数据的地形改正问题，最常用的方法是选取一系列地形改正密度值进行试算，将与地形相关性最小的布格重力异常确定为最佳重力异常，对应的密度为最佳地改密度[11]。使用该方法时，密度间隔取值太小，计算量过大；反之密度间隔取值太大时，可能不能获取最佳地形改正密度。常用的选取方法是以0.05×103kg/m3为步长进行计算，即便如此，若在(2.0～2.7)×103kg/m3的范围内进行试算，也需15次地形改正计算，工作量非常大。在给定的区间内采用二分法选取密度值进行地形改正计算[10]能在一定程度上减小工作量，但若想得到较准确的最佳地改密度，仍然需要多次计算才行。而本文提出的方法只需有限的几次计算即可得到最佳地改密度，工作量较小。

九嵕山实测重力资料校正时，全区采用的统一的密度。其原因在于地表地质调查结果表明研究区出露的地层较为单一，可以用统一的密度去等效实际地层的密度变化。此外，自由空间重力异常与测点高程的回归分析结果可以较好地用线性函数拟合，也反映出该区地形改正密度无明显的横向变化。实际工作中，若测区面积较大，可利用自由空间重力异常与测点高程的散点图进行判断，若线性函数拟合误差较大，则可采用分区处理的方式，最终再将校正结果拼接即可。

本文将布格重力异常与地形起伏变化无关作为判断布格重力异常校正是否合理的标准，事实上其为山区地形改正时的普遍原则。然而，实际工作中，必须针对勘探的具体目标进行具体分析。例如区域重力调查中，通常会采用统一的中间层密度(一般取为地壳平均密度2.67×103kg/m3)进行校正以方便数据拼接及对比，此时布格重力异常通常与地形呈现镜像关系，区域性的重力变化反映了地壳厚度的变化特征。在局部重力测量时，布格重力异常也可能表现为与地形同像的特征，例如盆山结合部位，造山带通常由变质岩、火成岩等组成，而盆地内部沉积层较厚，会使得重力异常呈现山区高、盆地低的特征，这种同像的重力异常是符合地质意义的，若研究盆山构造特征，则不能简单的以布格重力异常与地形无关而判断。而本文中的九嵕山地区，勘探目标为昭陵墓道口及墓室，其为近地表局部异常，因此整个山体引起的重力变化为非目标异常，布格重力异常的计算过程也相当于消除了区域背景。因此，实际工作中应将地形校正的过程与布格重力异常的后续处理结合起来，以提取勘探对象引起的重力异常为最终目的，若在地形校正时采用地壳平均密度等常密度值进行校正，则在重力资料处理时需要采用一定的措施消除或减弱与勘探目标无关的异常；相反，若在地形校正时采用了分区校正、变密度校正等措施已在一定程度上减弱了非勘探目标的重力影响，则在重力资料处理中可针对性的进行处理即可。

6 结论

针对山区重力测量时地形改正密度选取不准确引起的山形异常问题，本文以九嵕山重力异常为例，基于回归分析方法选取了最佳的地形改正密度，改正后的布格重力异常明显不受地形影响，证明了这一方法的正确性。本文使用回归分析方法时，采取了迭代计算的措施，与常规的采用一系列密度值进行试算的方法相比，本文方法可以快速获得最佳地形改正密度。从九嵕山地区的重力测量工作来看，现有技术条件高精度地形数据获取已不是难点，以实际地质构造为约束的改正方法及匹配的数据处理方法，是改进重力改正效果及提高解释精度的关键之一。