逻辑推理“落地” 数学素养“开花”
——一次基于“问题”为导向的研究性学习案例
2021-12-23周赛龙储炳南
周赛龙 储炳南
(安徽省合肥市第四中学 230000)
1 问题的提出
《普通高中数学课程标准(2017年版)》附录2——教学与评价案例25“覆盖问题”中就有这样一个问题:“以平面几何为知识载体,证明周长一定的四边形中正方形所围成的面积最大”.该案例旨在通过此问题就“如何培养学生逻辑推理的数学学科核心素养”作指导说明,但是,对于该问题的证明,课程标准中却仅仅提供了简要的证明路径(如图1),并未用数学语言进行严谨地推理论证.在教学过程中,笔者将其作为一次研究性学习活动课的内容,在设计课堂教学时,以问题为导向,通过向学生提出渐进的数学问题,并通过系列问题的解决,使学生严谨的逻辑推理能力得到了有效提升。以下,是笔者的教学过程实录,供同行们参考。

图1
2 问题的探究
思路1如图1所示,以四边形的边作为问题的切入点,采用列举、筛选的方法考察各种边长形式的四边形,逐一排除面积较小的四边形,构建一个递进式的证明路径.
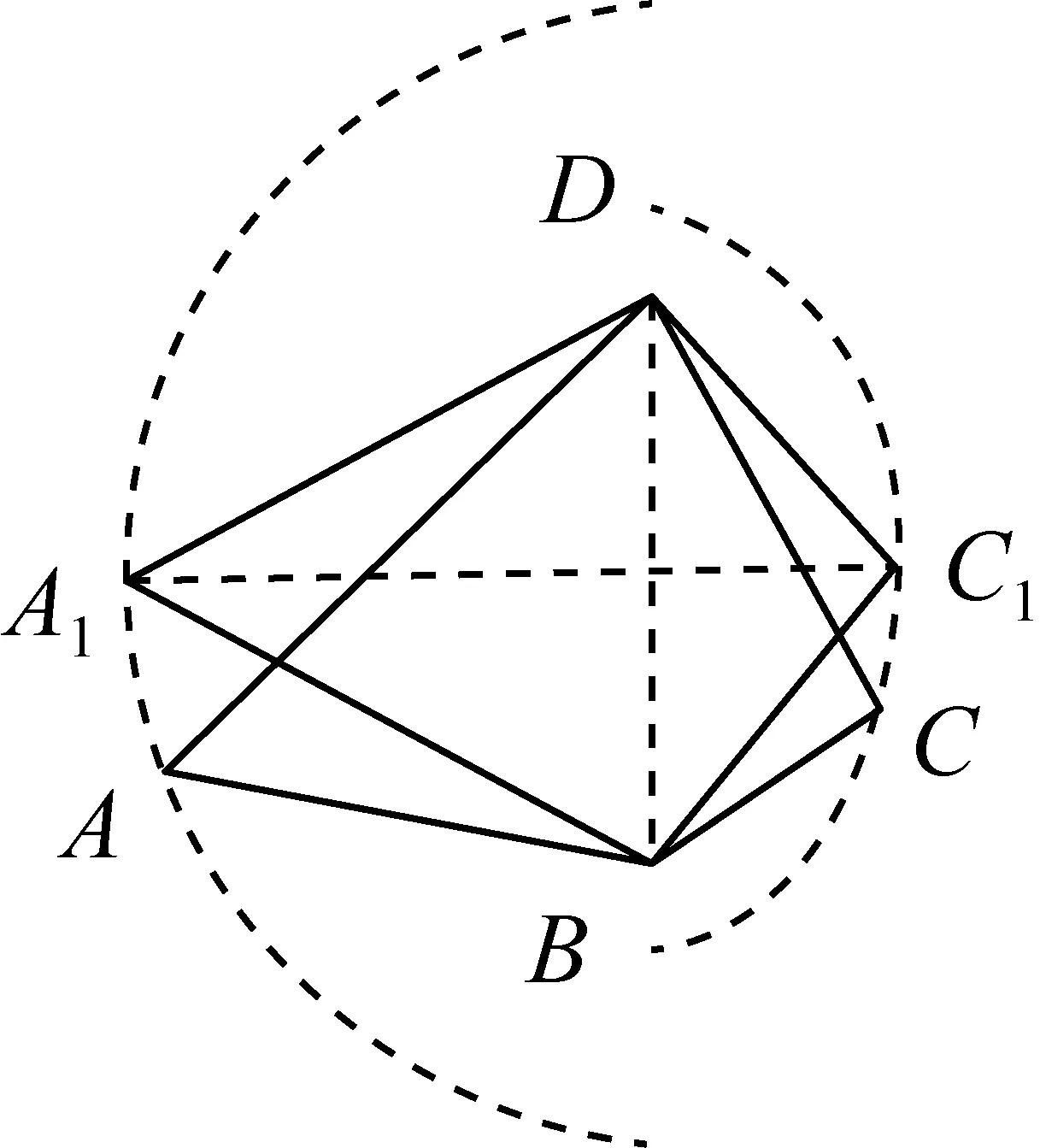
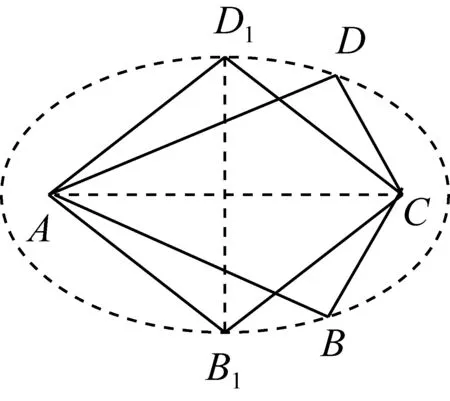
探究过程首先,为了证明S凹四边形 问题1如图2所示,已知凹四边形ABCD,连接BD,作点C关于直线BD的对称点C′,连接DC′、BC′,此时,凹四边形ABCD与凸四边形ABC′D的周长与面积各有怎样的大小关系? 图2 结合对称的性质,学生很快得到结论:凹四边形ABCD与凸四边形ABC′D的周长相等,此时,显然有S凹四边形ABCD 接着,为了证明S凸四边形 问题2如图3所示,已知凸四边形ABCD周长为定值l,记AB、BC、CD、DA长度分别为a、b、c、d,连接对角线BD,BD=e.若a+d=m(m为定值),问:当四边形ABCD各边满足什么条件时,S四边形ABCD最大? 图3 学生1:结合海伦公式以及均值不等式,很快给出了如下代数证明: 因为 S△ABD 当且仅当“a=d”时,“=”成立, 因为a+d=m为定值,所以b+c=l-m也为定值.故同理可得: 当且仅当“b=c”时, 所以(S四边形ABCD)max=(S△ABD)max+(S△BCD)max= 此时,“a=d”,“b=c”,四边形ABCD为筝形. 在学生1完成此证明后,老师又问学生:有没有其他不同的证明方法呢? 学生2:同学1代数法证明此问题的主要数学工具是基本不等式,而基本不等式可以构造平面图形进行几何解释,所以,针对此问题我们也可以考虑从平面几何的角度进行证明,具体如下: 在△ABD中,a+d=m为定值,且m>e,故点A在以点B、D为焦点的半椭圆上运动,同理,b+c=l-m也为定值,故点C也在以点B、D为焦点的半椭圆上运动,如图4所示.作对角线BD的中垂线分别交两椭圆于A1、C1,由图4易知,当点A与点A1重合时,△ABD的高最大,故S△ABD最大,此时AB=AD.同理,当点C与点C1重合时,S△BCD最大,此时CB=CD.综上可知:AB=AD,CB=CD时,S四边形ABCD最大,四边形ABCD为筝形. 图4 学生1在熟悉的问题情景中,能够有逻辑地去思考问题,通过观察条件和结论之间的内在逻辑关系,并利用基本不等式进行有条理地论证,体现了学生扎实的逻辑思维能力;学生2能够在综合的问题情景中,把握事物的关联,创造性地给出利用几何方法解决问题的方案,是学生高水平逻辑思维素养的重要体现.这种几何构造法是对代数法证明的解释和补充,通过数形结合的双重论证,问题2得到近乎“完美”地解决. 为了证明S筝形 问题3如图5所示,已知凸四边形ABCD周长为定值l,记AB、BC、CD、DA长度分别为a、b、c、d,对角线AC=e.若a=d,b=c,问:当四边形ABCD各边满足什么条件时,S四边形ABCD最大? 受到问题2中平面几何知识证明思路的启发,学生很快就类比得到如下证明方法: 如图5所示,作对角线AC的中垂线分别交两椭圆于B1、D1, 图5 因为a=d,b=c,且四边形ABCD周长为定值l, 所以点B、D均在以点A、C为焦点的椭圆上运动,如图5所示. 与问题2的几何证明类似,当点D与点D1重合,点B与点B1重合时,S四边形ABCD最大,此时,AB=AD=CB=CD,四边形ABCD为菱形. 最后,为了证明S菱形 问题4如图5所示,在问题3的基础上,当菱形AB1CD1周长为定值l时,菱形AB1CD1满足什么条件时面积最大呢? 学生很容易就得到了: 至此,活动的任务“证明周长一定的四边形中正方形所围成的面积最大”得到了完全解决,但笔者仍觉得此次教学活动并不完美. 一方面,虽然问题解决的视角十分简洁、巧妙,但解决方式却过于单一化,除问题2外,主要依靠平面几何方法进行推证.因此,为进一步训练学生代数推理方面的逻辑思维能力,老师又向学生提出了问题5. 问题5问题3是我们类比问题2中学生2的平面几何方法证明的,同样地,同学们能否类比问题2中学生1的代数方法,对此问题进行重新证明呢? 在教师的启发下,通过类比探究,学生3利用柯西不等式,找到了一种既清晰又简洁的代数证明方法,具体如下: 学生3从代数角度的证明不仅是对问题3、4几何法证明的补充和完善,还简化了问题证明的路径,由“筝形”直接到“正方形”,直达结论.至此,每个问题环节都从代数与几何两个方面进行了双重论证,学生的代数推理、几何论证、类比推理等逻辑思维能力均得以训练,整个问题也得到了系统全面的解决. 在整个问题的证明过程中,学生证明方法的获得,是在教师预设的递进式问题中依次进行的,这种渐进式问题的设置,就是告诉学生,将一个“复杂的问题”转化为若干个“简单问题”是进行数学思维的一种惯用的逻辑推理方式. 为了进一步发挥本次研究性学习的教学效果,将教学课堂延伸到课外,在活动结束前,教师又给学生布置了一个课后探究性学习任务:“对于上述问题,请同学们探究一下,还有其它的证明方法吗?”惊喜的是,众里寻他千百度,蓦然回首,那人就在“青出于蓝”处.经过课后探究,学生4提供了一个新的证明思路如下. 思路2我们常说,周长相等的平面图形中,圆的面积最大.在任意的四边形中,直观上我们感觉圆内接四边形是与圆最接近的,故做大胆猜测,可按照“任意四边形→圆内接四边形→正方形”的路径进行问题证明.具体证明过程如下: 问题6如图6所示,已知四边形ABCD周长为定值l,面积为S,记AB、BC、CD、DA长度分别为a、b、c、d,BD=e、∠BAD=α、∠BCD=β. 图6 问:当四边形ABCD满足什么条件时,S四边形ABCD最大? 得4S=2adsinα+2bcsinβ; ① a2+d2-b2-c2=2adcosα-2bccosβ; ② ①2+②2得16S2+(a2+d2-b2-c2)2 =(2adsinα+2bcsinβ)2+(2adcosα-2bccosβ)2 =4a2d2(sin2α+cos2α)+4b2c2(sin2β+cos2β)-8abcdcos(α+β) =4a2d2+4b2c2-8abcdcos(α+β), 所以当α+β=π时, [16S2+(a2+d2-b2-c2)2]max =4a2d2+4b2c2+8abcd, 此时,整理得 S=[(a+b+c-d)(a+b+d-c)(a+c+d-b)(b+c+d-a)]1/2/4. 因为α+β=π,所以此时四边形ABCD为圆内接四边形.又因为 [(a+b+c-d)(a+b+d-c)(a+c+d-b)(b+c+d-a)]1/2/4 当且仅当“a=b=c=d”时“=”成立. 学生4能够在综合的问题情境中,与关联知识进行类比推理,正确地构造了过渡性命题,创造性地构造证明路径,利用代数推理的方法合理地解决了问题,并用严谨的数学语言表达了论证过程,体现了学生4高水平的逻辑推理素养,同时,也侧面反映了本次以“覆盖问题”为载体,以提升学生逻辑推理学科素养为主要目的的研究性学习活动开展成功.最终,本次研究性学习活动以“无憾”结束. 逻辑推理是高中数学六大学科素养之一,它是数学严谨性的基本保证,也是发现数学结论、构建数学体系的重要方式,更是人们在数学活动中进行交流的基本思维品质[2].然而,在培养学生逻辑推理能力的过程中,仅仅将教学单一地停留在如何解题层面是远远不够的,只有让逻辑推理在教师教学过程中落地,才能让数学素养在学生学习过程中开花. 问题是数学的心脏,发现并提出新问题要比解决一个问题更有价值;问题意识是设法解决问题的内在驱力,有计划、有意识、有目的地引导学生积极回答问题、培养问题意识要比硬“灌”给学生各式各样的解题的方法更有意义;问题的探究是学生有机地串联知识,不断地深化思考,强化逻辑的过程,所以,探索和表述问题的论证思路也要比问题本身的结果更加重要.因此,在探究问题的过程中,教师在注重结果导向的同时,更要把握好过程意识,只有密切关注到探究过程中学生思维的产生、发展、构建与表达,积极引导学生多角度、多层次地对问题进行归纳、类比与演绎,及时抓住学生思考过程中思维的创新点,才能达到训练逻辑思维、提升核心素养,把握问题本质、最终创造性地解决问题的教学目的. 在研究性教学活动中,基于问题导向的数学教学大概有三个层次,低层次是训练学生的解题能力,中层次是提高学生的思维能力,高层次是提升学生的数学素养[3]. 因此,培养学生逻辑思维素养的教学绝不是一蹴而就的,而是一个由低到高的循序渐进过程. 另外,为了达到高层次的教学水平,教师千万不要怕学生犯错,大胆地放手让学生去做,把教学过程中最精彩、最出彩、最有价值的部分留给学生去探索、去思考、去创造,在潜移默化中达到对学生逻辑推理素养培养“润物细无声”的效果.相信学生,历经“山重水复”方能“无疑路”,看遍“柳暗花明”终将“又一村”.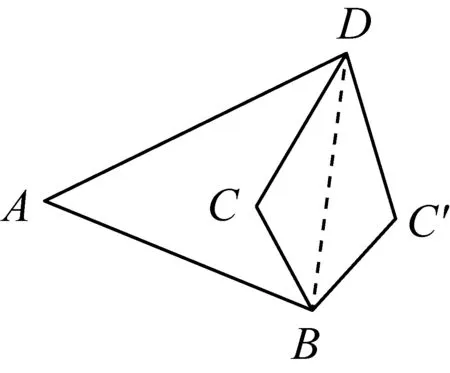



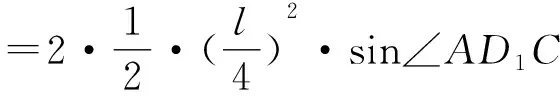
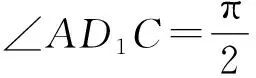

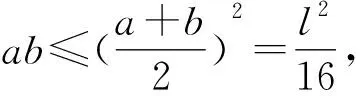
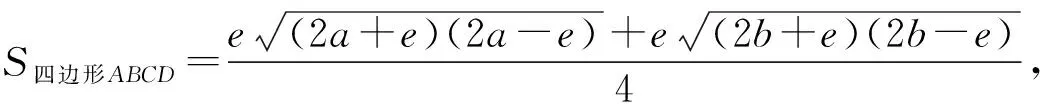
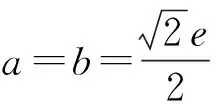

3 问题的再探究



4 问题的反思总结
