一种低信噪比突发信号载波跟踪技术研究
2021-12-23刘永桦王鹏毅王西夺
刘永桦,王鹏毅,王西夺
(中国电子科技集团公司第五十四研究所,河北石家庄 050081)
在某些低轨卫星通信系统中,为了提高地面站同时服务卫星的数量,采用分时方式完成卫星接入管理,需要卫星利用短突发扩频信号的形式向地面汇报自身状态、位置等信息。低轨卫星为了节约能量,限制发射天线功率,使得下行信号信噪比较低;同时卫星与地面站间存在高速的相对运动,使得下行信号具有较大的多普勒频率及变化率。在扩频接收机中,载波跟踪是信号解调、译码的前提,在低信噪比条件下,信号高动态特性对跟踪解调性能的影响更为严重,在突发模式下更是如此。因此,研究短突发信号的快速载波跟踪技术具有很大的实际意义。
传统载波跟踪算法主要使用锁相环对扩频信号进行载波跟踪,为了解决低信噪比高动态条件下的应用问题,研究人员对锁相环进行改进:其一是使用锁频环辅助锁相环的形式[1-2];其二是根据鉴别器输出结果实时改变环路滤波器带宽[3-4];其三是使用现代滤波算法[5](如传统卡尔曼滤波算法、扩展卡尔曼滤波算法)代替传统环路滤波器。以上方法多应用在长时间连续信号中,难以在很短的时间内实现快速同步,因此对突发信号用于载波同步的导频信号长度有一定要求。而现有基于前向结构的突发信号载波同步算法[6-7]通过直接从信号中估计载波频率及相位精确值完成同步,需要满足一定的信噪比条件,因此在当前低信噪比、高动态应用场合性能恶化严重。
本文从工程应用角度出发,提出一种低信噪比短突发信号的载波跟踪算法,此算法采用基于多普勒变化率补偿的跟踪结构,并对算法进行优化设计,进一步提高了数据利用效率,在低信噪比、高动态场景下得到较高的跟踪精度。优化后的算法复杂度适中,在提高接收机载波跟踪性能的同时易于工程实现。
1 卫星下行突发信号模型
卫星下行信号调制的信息按照发送顺序分为导频序列、帧头、数据序列3个部分,信号模型如图1所示。其中导频部分符号已知,用于在低信噪比条件下实现突发信号的快速捕获并引导跟踪进入锁定(后文所称导频序列均指用于跟踪模块引导入锁的信号部分),帧头部分用于确定数据开始位置与帧同步,数据部分按照设计文件传输卫星信息。

图1 卫星下行信号模型Fig.1 Satellite signal model in downlink mode
卫星下行信号采用BPSK直接序列扩频体制,在加性高斯白噪声信道下,假设接收信号在经过信号捕获、码同步解扩后,进入载波跟踪模块的信号模型可以表示为
r(k)=AD(k)exp(jφ(kTS))+w(k),
(1)
式中:A为信号幅度;D(k)为调制的信息比特;TS为采样间隔;φ(kTS)为当前时间信号相位;w(k)为复高斯白噪声。
由于卫星与地面站之间的相对运动会产生多普勒效应,接收机接收到的卫星下行信号具有较大的动态[8],即接收信号中频与接收机本振之间出现多普勒频偏与多普勒高阶变化率。根据低轨卫星与地面站的相对运动分析,相比于信号多普勒频率的一阶变化率,其二阶变化率相对较小,不是影响跟踪环路动态应力的主要原因。因此在信号持续时间内载波可以被视为一个线性调频(LFM)信号,其瞬时频率随时间呈线性变换。在此条件下,当信号初始接收相位为φ0、信号多普勒初始频率为f0、多普勒一阶变化率为f1时,接收信号模型可改写为
r(k)=AD(k)exp(j(φ0+f0·kTS+
(2)
2 载波跟踪原理
扩频接收机解调过程包括信号捕获、扩频码跟踪、载波跟踪、位同步、译码等步骤。由于扩频码速率相较于载波频率低,受多普勒效应影响较小,在正确完成捕获后可以在损失一定信噪比的条件下完成信号解扩。在低信噪比条件下,接收机载波跟踪过程对多普勒影响更为敏感,直接影响后续解调数据的正确率。
本文研究的突发信号使用相干解调方式,需要接收机在本地生成一个与接收信号同频同相的相干载波,来完成载波剥离与数据解调。现有接收机使用科斯塔环进行载波跟踪[9],由于多普勒频移现象的存在,使接收信号频率和设定频率之间发生明显变化,因此需要载波跟踪环路不断调整本地信号的相位,使得接收信号载波与本地信号之间的相位差值始终保持在较小的范围内,即可认为达到了锁定状态,从而可以通过相干解调获得载波上调制的数据。数字锁相环通常由鉴相器、环路滤波器与数控振荡器组成,其结构如图2所示。

图2 科斯塔锁相环结构Fig.2 Structure of Costa phase locked loop
在低信噪比高动态环境下,锁相环的跟踪性能主要由环路滤波器决定。环路滤波器的阶数以及参数设计决定了环路噪声带宽BL,而BL的大小决定噪声进入环路的多少。当带宽BL变窄时,环路的滤波效果更好,环路对信号的跟踪就越精确。但带宽BL过窄时,由于高动态信号中的有用高频分量会随噪声一起被滤除,使其动态跟踪性能减弱,可能造成环路失锁。
在信号捕获完成后,接收机已经得到信号载波频率的初步估计值,在通过锁相环进行载波相位精确跟踪时,对跟踪性能产生影响的主要是捕获后的剩余频偏以及频率变化率。根据理论分析,当输入信号分别为频率阶跃信号(多普勒频率为恒值)和频率斜升信号(多普勒一次变化率为恒值)时,不同阶数的锁相环得到的稳态误差如表1所示。

表1 锁相环稳态跟踪误差Tab.1 PLL steady state tracking errors
由表1可以看出,二阶锁相环可以跟踪频率斜升激励,但是会产生一个恒定的跟踪误差,三阶锁相环可以准确无误地跟踪上频率斜升信号。环路滤波器阶数越高,对信号的动态跟踪能力越强。在相同阶数的环路滤波器中,越大的带宽可使接收机具有越强的动态跟踪能力,但也降低了跟踪精度。同时,在低信噪比条件下,接收机往往需要进行长时间的积分累积来消除噪声影响,而信号的高动态特性使得信号能量不能有效积累,因此高动态信号在进行载波跟踪时对噪声更为敏感。
对于进入跟踪模块的接收信号r(n),使用三阶锁相环进行载波跟踪时,较大的频率变化率会使环路需要较长的时间进入锁定状态,同时为了适应信号动态,选用更大的环路带宽会使跟踪精度降低。由于接收信号中导频序列长度有限,在经过接收机信号捕获、码同步等模块消耗后,当可供跟踪环路消耗的导频长度不足使环路进入锁定状态时,会导致信号上调制的有用数据丢失,造成跟踪解调失败。
3 突发信号载波跟踪算法设计
为了避免丢失有用信息,接收机必须在较短的信号序列内完成信号捕获跟踪,并完成对后续信号序列的正确解调。相比于一些突发通信中使用开环结构,利用频率估计完成快速载波同步[10-11],在低信噪比条件下使用锁相环等反馈结构进行载波跟踪对信号的动态适应能力与跟踪解调性能更为优良[12-13],但在较高动态环境下需要较长的跟踪入锁时间。因此,本文重点在信号捕获和伪码跟踪基础上使用改进的反馈跟踪结构完成载波跟踪,提高接收机跟踪解调性能。
3.1 频率变化率估计辅助的载波跟踪算法
接收到的信号经过下变频、捕获等前置模块后,接收机对信号的频率及码相位进行粗估计[14],多普勒参差满足伪码环工作条件,伪码环开始工作,对接收信号进行解扩。相比载波同步,信号动态对码相位同步影响较小,算法较成熟,本文不再详述,而重点研究在伪码跟踪基础上如何快速进行载波稳定跟踪。
由锁相环原理分析可知,使用传统三阶锁相环可以对当前信号进行正确跟踪,但环路噪声带宽BL必须在低噪声与高动态性能之间作出艰难的平衡,需要对信号动态进行估计以降低环路滤波器的动态应力。考虑到在低信噪比、高动态场景下,当前突发信号仅能利用已知调制信息的导频序列对信号频率参数进行的估计,本文算法利用一部分导频序列完成信号多普勒和多普勒变化率的估计,根据估计结果辅助三阶锁相环进行载波跟踪,以降低跟踪失锁率和平均误码率。
解扩后的信号进入载波跟踪模块时,首先进入多普勒估计模块,对前置的导频序列进行一段时间的多普勒频率及变化率估计,后续信号进入估计值辅助三阶锁相环进行载波跟踪及数据解调。其中,算法的核心模块是多普勒频率及变化率估计模块。对于当前低信噪比、高动态信号,由于信号频谱存在频谱扩散现象并受到较大的噪声影响,常规傅里叶分析不能得到较高精度的估计值,甚至可能得到错误的估计值。而相较于一些文章中使用的分数阶傅里叶变换算法[15],本文算法通过结合短时傅里叶变换(STFT)与最小二乘拟合(LSM)算法进行频率及变化率估计,是一个简单有效的解决方案。频率变化率估计辅助的载波跟踪算法结构如图3所示。

图3 频率变化率估计辅助的载波跟踪算法结构Fig.3 Algorithm structure of carrier tracking assisted by the estimation of frequency change rate
短时傅里叶变换利用一个移动的窗函数将信号在不同时刻的部分依次取入窗口,在窗函数内认为信号频率是不变的,然后对窗内的信号进行FFT变换,可以避免窗外信号的干扰[16-18]。随着窗函数在时间轴上的移动,得到了不同时间段内信号的短时频谱,时频分析结果可以推断信号的时变特性。短时傅里叶变换示意图如图4所示。

图4 短时傅里叶变换示意图Fig.4 Schematic diagram of short-time Fourier transform
对于采样后的离散信号STFT的定义为
(3)
式中:x(k)为待分析的信号;w(k)为窗函数;G(m,n)中的m,n分别对应STFT的时间和频率参数;N为窗函数的窗长;s为相邻窗的移动步长。
利用STFT可以得到所分析信号不同离散时间点对应的多个频率估计值。为了通过分析导频信号得到整段信号的频率估计值,需要在STFT结果的基础上估计信号的频率变化率。本文算法中采用最小二乘拟合(LSM)算法对导频序列STFT结果进行处理,得到整段信号的初始频率及频率变化率的估计结果,并以此来推算整段信号的瞬时频率。

使用最小二乘拟合可以在一定程度上提高估计结果的精度,但对于当前信号频率变化率估计算法中,估计精度主要受STFT分析精度的影响。在低信噪比条件下,需要较长的窗长对信号频谱能量进行累计,避免被噪声淹没,而在较高动态的条件下,信号频谱能量又会发生扩散,因此对于STFT来说,窗长N为决定其时频分析效果的最重要参数,需要根据信号特性对窗长进行选择。
由于高动态环境会导致信号频谱主瓣宽度增加,峰值高度下降。根据能量守恒定律,当信号发射功率不变时,不同动态条件下频域总能量应该保持不变[19]。定义信号与噪声能量谱高度比HSNR为
HSNR=HS/Pw=A2N/σ2。
(4)
HSNR越大,表明目标信号对比基底噪声突出的幅度越明显,也就越有利于信号检测和参数估计。对于仅存在一次变化率的线性调频信号,其信号与噪声能量谱高度比计算公式如下:
(5)
式中:WS,WL和HS,HL分别为频谱扩散前后的双边主瓣宽度和峰值高度。


图5 信号动态对HSNR结果影响Fig.5 Effect of signal dynamics on HSNR results
由图5可以看出,在不同动态、同一低信噪比条件下,信号频域的HSNR不再随N的增加而单调递增,因此无法仅利用长时间积分的方式来提高频域主瓣峰值。当信号变化率增大时,HSNR随窗长的变化曲线形状改变,最大值单调下降,对应的窗长变小。考虑到实际情况下接收到的多普勒变化率未知,为了提高信号窗内的最小HSNR值,因此窗长选择按照可能残余的最大多普勒变化率f1max进行计算。
根据搜选窗长对估计所用导频序列进行STFT后可以得到若干个频率估计值。考虑到低信噪比条件下,窗长较短的STFT可能在某个窗口出现信号频谱峰值被噪声淹没,不能得到正确的频率估计值。为了避免误差较大的频率估计值会对拟合结果产生严重影响,在拟合后需要进行野值剔除,去除明显不正确的估计值[20]。对于STFT估计结果,在进行一次拟合后,估计结果与拟合结果之差可以近似认为符合正态分布。根据莱特准则,需要将残差落于3倍标准差区域外的测量数据作为野值进行剔除。因此在完成一次拟合后,对估计值进行野值检测,如果存在野值就进行剔除并再次拟合,可以进一步提高信号频率及频率变化率估计的精度。
3.2 算法优化设计
根据对高动态信号频率估计算法分析,当频率估计所用信号总长度越长,算法估计精度越高。但由于卫星下行信号持续时间较短,可供频率估计模块利用的序列长度有限,估计结果与信号真实频率及变化率存在一定误差。在频率估计辅助的载波跟踪算法中,较大的频率估计误差使得锁相环不能迅速进入锁定,因此仍需要利用一定长度的导频序列完成频率牵引及相位锁定。
为了提高数据利用率,减小跟踪所需导频序列长度,在频率估计辅助的载波跟踪算法的基础上进行改进,提出了一种迭代载波跟踪算法。其主要改进思路为增加一个储存模块,将解扩后的信号数据降采样并存储。对存储的数据采用前文估计算法进行多普勒和多普勒变换率估计,并利用估计结果对储存的数据进行多普勒和多普勒变化率补偿,从而实现对存储数据的迭代处理,用动态更低的信号代替原有储存的信号,迭代完成后通过锁相环对储存的全部信号实现较高精度的跟踪解调。
由于信号在进入载波跟踪模块前已经完成解扩过程,同时信号数据速率远小于扩频码速率,因此对信号进行降采样可以大幅降低数据量,有利于工程实现。改进后的算法根据估计值对储存模块的数据进行迭代处理,不仅降低了信号对锁相环的动态应力,而且实现了对导频序列信息的重复利用。将迭代前的导频序列用于频率参数估计,而迭代后的导频序列用于锁相环入锁,在提升载波跟踪性能的同时可以有效提高卫星下行短突发信号的数据利用率。
迭代载波跟踪算法主要分为以下步骤:
1)对解扩后信号进行降采样并储存至信号储存模块;
2)提取信号中的导频部分,并根据预设信息完成导频去调制;
3)对调制的导频序列按照最佳窗长进行STFT得到频率估计值,对估计结果进行剔除野值的最小二乘拟合,得到信号初始频率估计值与频率变化率估计值;
4)根据估计的频率及变化率,利用本地振荡器生成一段与接收信号动态相近的本地载波,并在储存模块中原始信号进行多普勒动态补偿;
5)迭代后信号仍存在一定残留初始频偏及频率变化率,因此选用带宽较小的三阶锁相环完成对信号的载波同步及数据解调,得到调制的数据序列。
迭代载波跟踪算法流程如图6所示。
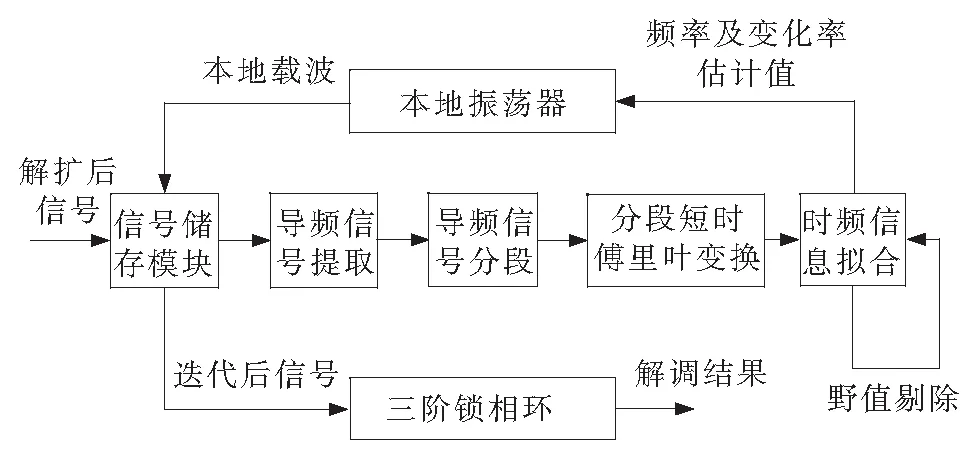
图6 迭代载波跟踪算法结构Fig.6 Algorithm structure of iterative carrier tracking
4 仿真分析
根据卫星下行信号结构与特点分析,调制有随机数据的信号模型。根据前置模块性能指标,设定进入跟踪模块信号的频率偏差在±200 Hz以内,信号频率变化率在±2 kHz/s以内。在-170 dBW条件下,由于接收机热噪声影响,接收机等效载噪比约为34 dBHz,考虑到一定的解扩损失,进行载波跟踪时假设接收信号等效载噪比为33 dBHz。仿真时信号数据速率为1 Kb/s,并采用BPSK调制方式,此时信号误码率理论值根据公式
折算约为2.29%。
通过蒙特卡罗仿真对比,导频序列后的随机数据序列设定值与解调结果计算误码率,若数据部分的平均解调误码率>5%时,认为此次跟踪不成功,最终以跟踪成功率与平均误码率作为算法性能衡量标准。
4.1 锁相环载波跟踪动态性能
当对不同动态信号直接使用三阶锁相环进行载波跟踪时,根据3.2分析可知,在低信噪比条件下,短突发信号的初始多普勒频偏以及频率变化率均会对接收机载波跟踪性能产生明显影响。同时设定信号跟踪入锁所用导频序列长度150 ms,通过蒙特卡罗仿真计算跟踪成功率与平均误码率,仿真结果如图7所示。
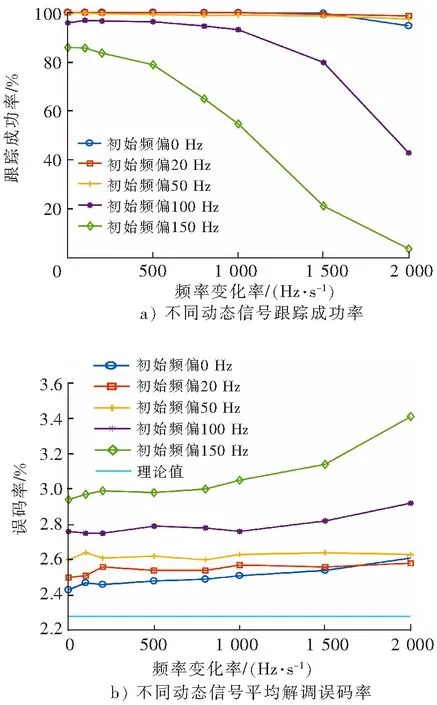
图7 三阶锁相环对高动态信号适应能力Fig.7 Adaptability of third-order PLL to high dynamic signals
仿真结果可以看出,当初始频偏较小时,频率变化率不会对跟踪成功率以及解调误码率产生明显影响。但是当初始频偏较大时,由于前置导频序列长度有限使得锁相环入锁时间受限,导致跟踪成功率明显下降,同时为了完成跟踪,使用较大的环路噪声带宽引起解调误码率有明显上升,因此三阶锁相环在信号动态小时工作性能良好,但在信号动态大特别是初始频偏大时性能恶化严重,不能直接完成对当前条件下信号的载波跟踪。
4.2 多普勒估计误差仿真分析
通过分析迭代载波跟踪算法可知,其频率估计模块的估计精度决定迭代后信号的动态大小,而对相同长度导频序列进行频率参数估计时,影响估计精度的主要参数为STFT补零长度与STFT之间的滑动间隔。
根据信号多普勒变化率最大为2 kHz,由STFT窗长公式计算出单次STFT长度为30 ms,利用100 ms导频信号进行频率参数估计,进行蒙特卡罗仿真,取估计结果最大值。估计模块参数对估计精度影响如图8所示。
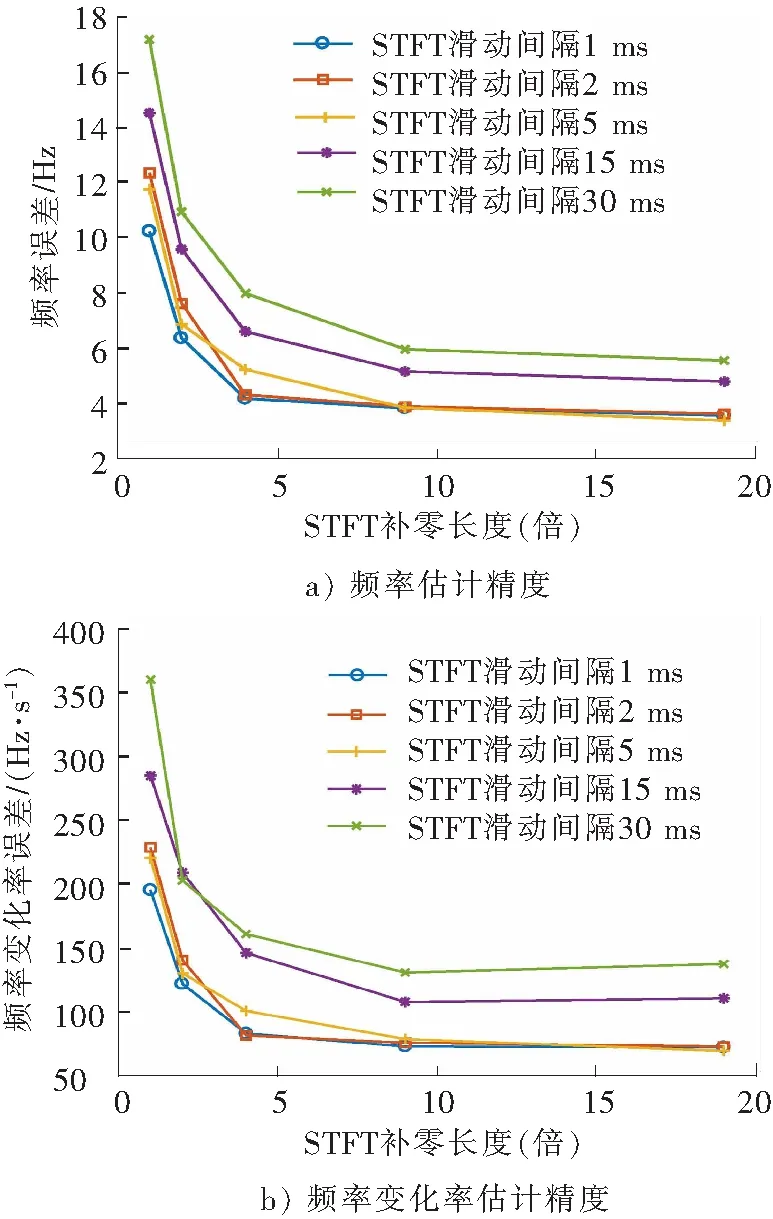
图8 估计模块参数对估计精度影响Fig.8 Effect of estimation parameters on the estimated performances
由图8可以看出,随着STFT补零长度的提高,单次STFT的频谱分辨率也随之提高,从而提高拟合后的频率及频率变化率估计精度。另一方面,通过减少STFT滑动间隔,可以为拟合提供更多数据,因此也可以降低噪声对估计结果的干扰,从而得到更小的估计误差。考虑到提高STFT补零长度与减少STFT滑动间隔均会增加对系统运算资源的占用,因此需要在估计精度与运算量之间进行平衡。
4.3 迭代载波跟踪算法性能分析
对于卫星下行信号,信号的前置导频序列有限,而接收机需要在有限的长度内完成信号捕获、扩频码同步、频率捕获、相位锁定等多个环节,因此迭代载波跟踪中参数估计模块所能利用的导频序列有限。仿真条件同上,频率估计模块参数设置为STFT补零长度4倍,滑动间隔为1/20的估计信号总长度,使用蒙特卡罗仿真对不同估计所用导频长度的估计精度影响进行仿真分析。导频长度对估计模块精度的影响如图9所示。
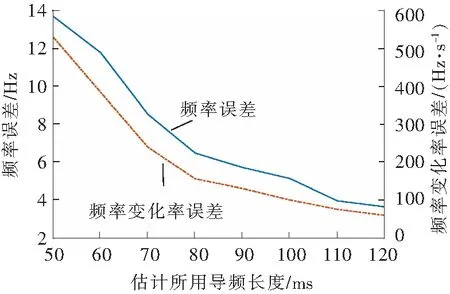
图9 导频长度对估计模块精度的影响Fig.9 Effect of preamble length on the estimated performances
由图9可以看出,随着增加估计所用导频序列长度,频率估计精度发生明显改善,对比使用50 ms导频序列进行估计的结果,使用60 ms导频就可以将频率变化率误差降低1/2,使用80 ms导频即可将频率误差降低1/2。使用120 ms导频估计时,频率及变化率误差分别降低为50 ms的1/4与1/7。
利用频率参数估计误差作为先验知识对三阶锁相环环路带宽进行设置,完成迭代载波跟踪算法蒙特卡罗仿真,计算载波跟踪正确率与平均误码率曲线。迭代载波跟踪结果如图10所示。

图10 迭代载波跟踪结果Fig.10 Results of iterative carrier tracking
由图10可以看出,使用迭代载波跟踪算法对卫星下行信号进行载波跟踪时,利用50 ms导频序列时跟踪成功率达到99%,平均解调误码率为2.62%,当长度增加至90 ms时,平均解调误码率下降至2.44%,跟踪解调损失由0.26 dB降至0.12 dB,可以满足后续译码需求。
以上仿真结果都是在灵敏度电平条件下得到的,在同样环路带宽下,当信噪比更高时,算法中频率及变化率估计精度与环路跟踪精度更高,解调损失更小。
5 结 语
本文提出了一种由短时傅里叶变换算法和最小二乘拟合算法相结合辅助三阶锁相环的迭代载波跟踪算法,该算法在较低信噪比下兼顾短突发信号的高动态性能和载波跟踪精度的要求下,可以快速进入频率锁定状态并得到误码率较低的解调结果。
与传统三阶锁相环相比,该算法可以用更短的前置序列完成大幅度频率牵引,同时通过迭代降低信号频率变化率,具有收敛速度快以及跟踪精度高的特点,克服了传统算法在低信噪比、高动态环境下对短突发信号进行跟踪时,跟踪稳定性差且解调误码率高的缺点。通过缩短跟踪所需导频序列长度,提高了信号数据利用率,同时算法复杂度适中,具有良好的工程应用价值。
但在更低信噪比或更高动态条件下,本文算法中频率估计模块的短时傅里叶变换由于噪声过大或窗长过短会导致不能得到正确的频率估计结果,使得迭代后的信号动态不能有效降低,影响后续载波跟踪性能,未来可以进一步针对更低信噪比或更高动态条件下的突发扩频信号载波跟踪进行研究。
