不同本构模型在开挖边坡有限元强度折减法中的应用

聂美军， 张坤勇，4， 杜 伟， 李广山， 张兴其

（1.河海大学岩土工程科学研究所，南京 210024； 2.中设设计集团股份有限公司，南京 210014；3.中车建设工程有限公司，北京 100078； 4.河海大学岩土力学与堤坝工程教育部重点实验室，南京 210024；5.合肥市市政设计研究总院有限公司，合肥 230001）

数值方法是计算边坡稳定性的常用方法［1-2］，其中应用广泛的有限元强度折减法可以计算复杂地质的边坡体，如非均质边坡［3］. 边坡土质的性质对本构模型的选择也有影响［4-6］. 合理的本构模型在分析边坡破坏的发生发展过程时能考虑到挖方或填方对边坡稳定性的影响［7-9］. 因为开挖边坡不同区域土体可能处于卸荷状态或加荷状态，所以开挖边坡土体中的应力和变形的分布规律也会产生变化，进而会影响到边坡的安全稳定性，而传统的极限平衡法并不能描述这种变化［10］.

边坡典型位置的变形可以在一定程度上反映边坡的“稳定状态”. 选用能够反映开挖施工过程的合理本构模型，是过程模拟的要求，也是采用以变形量为失稳判据的重要前提，对于开挖工程的土体变形预测、边坡稳定性分析是必要的. 本文采用能够反映开挖边坡土体应力状态和应力历史的本构模型，通过有限元数值计算，对边坡的开挖过程进行逐级分析，并与采用极限平衡法得到的稳定性安全系数和变形计算结果进行了比较.

1 剑桥系列本构模型理论

1.1 剑桥模型

剑桥模型是由剑桥大学罗斯科（Roscoe）等在1963年提出的. 该模型以室内三轴压缩试验为基础，通过引入加工硬化原理和能量方程推导出模型的屈服方程.

剑桥模型的屈服方程为

式中：p为平均应力；q为广义剪应力，它反映了土体在复杂应力状态下受剪的程度；σ1为大主应力；σ2为中主应力；σ3为小主应力；τoct为正八面体面上的剪应力；p0为p-q平面上的屈服面与p轴的交点，为初始平均应力；M为p-q平面上破坏线的斜率，为临界状态应力比.

式中：λ为压缩指数；κ为回弹指数；e0为初始孔隙比.

因为剑桥模型采用相关联的流动法则，综合式（1）～（4）即可得到剑桥模型的屈服函数f与塑性势函数g为

1.2 修正剑桥模型

剑桥模型以εpv作为硬化参量，其屈服轨迹在p-q平面上为子弹型，屈服面上与p轴的交点的法向矢量并不与p轴平行，这与经典的塑性理论是相违背的. Roscoe和Burland针对剑桥模型的这种缺陷做了修正，将剑桥模型的p-q平面上的子弹型修正为沿p轴等向硬化的椭圆曲线，这就是后来众所周知的修正剑桥模型［11-13］.

修正剑桥模型的屈服函数f为

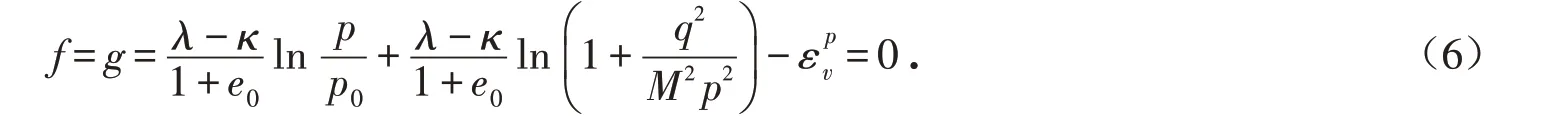
修正剑桥模型虽然克服了剑桥模型的缺陷，但是也有其局限性. 修正剑桥模型不能反映土体的剪胀特性、各向异性等土体实际的复杂性质，而且修正剑桥模型和剑桥模型一样，都是依据重塑土的室内试验结果提出来的，只能考虑土体在初始等向固结应力状态下的强度变形特性. 而实际天然土体一般都处于初始不等向固结状态（即初始K0固结状态），在某些实际工程中，甚至处于初始三向不等向应力状态. 土体实际的初始应力状态的不同会直接导致土体在承受附加荷载时变形特性的不同，而修正剑桥模型并不能合理地反映出土体的这种特性.

1.3 关口-太田模型

为考虑初始K0固结引起的应力各向异性，关口-太田于1977年提出了关口-太田模型［14］，该模型在剑桥模型的基础上通过引入新的应力比参数η*使得硬化轴得到旋转，同时将p-q平面上的屈服面由原来的p轴等向硬化变为沿K0轴不等向硬化. 和剑桥模型相比，关口-太田模型通过调整卸荷应力路径下的弹性区范围来模拟初始各向异性的影响，因此其可以在一定程度上反映开挖卸荷的影响.

为了反映土体初始不等向固结（K0固结）引起的各向异性，关口-太田模型引入了新的应力比参数，具体如下：

式中：σij为有效应力张量；δij为单位方向向量；Sij为偏应力分量.

将偏应力张量的积表示为

式中：τoct为正八面体面上的剪应力.

定义应力比：

式中：η为应力比；p0为K0固结完成时的初始平均应力；q0为K0固结完成时的广义剪应力；η0为K0固结完成时的应力比.

定义归一化偏应力张量：

采用ηij0=来表示初始K0固结完成时的ηij值，其中Sij0为K0固结下的偏应力分量；ηij0为K0固结下的归一化偏应力张量.

在上述公式基础上，定义新的应力比参数η*为：

关口-太田模型中，塑性体积应变由固结和剪胀引起，即：

由于黏性土具有剪胀特性，其剪胀系数可定义如下：

因此，可以得到由剪胀引起的塑性体积应变为：

综合以上各式可得：

则关口-太田模型的屈服方程为：

而当土体状态为初始等向固结时，有

同时

从而有

式中：σij0为K0固结下的有效应力张量.

进而有

此时，关口-太田模型即退化为剑桥模型，其屈服方程也相应地退化为：

1.4 修正关口-太田模型

此外，有学者［15-16］在关口-太田模型的基础上将p-q平面上的子弹型屈服面进一步修正为沿η*不等向硬化的椭圆形屈服面，进而得出修正关口-太田模型，该模型在p-q平面地屈服方程为：

2 几种模型的比较

2.1 不同模型对偏载作用下地基变形计算比较

关口-太田模型通过硬化轴的旋转来反映土体的初始各向异性的思想可以简单地理解为：对于经过硬化轴旋转的模型考虑了初始不等向固结由于硬化轴旋转而产生的塑性体积应变，而实际土体一般处于初始K0固结状态，因此土体在开挖卸荷应力路径（即广义剪应力q减少）下，即使平均应力p保持不变，由于模型的硬化轴发生偏转，土体也会产生一定的塑性变形.

关口-太田模型存在着和剑桥模型类似的缺陷，即当模型退化为等向固结的剑桥模型时，会导致等向固结条件下仍有塑性剪应变分量. 因此，将关口-太田模型p-q平面上的子弹型屈服面修正为椭圆形屈服面，即得到修正关口-太田模型.

采用简单算例对以上剑桥系列弹塑性模型计算结果进行对比，算例模型如图1所示，模型尺寸为20 m×15 m，底部约束住x和y方向的自由度，两侧只有x方向约束，y方向自由. 偏荷载分布在2.5 m范围内，分两次施加，第一级荷载q1=50 kPa/m，第二级荷载q2=100 kPa/m. 计算采用的参数如表1所示.

图1 模型尺寸及荷载Fig.1 Model size and load

表1 计算采用的参数Tab.1 Parameters used in the calculation

如图2所示，图中的A点为K0固结状态，在广义剪应力减小时保持平均应力不变，其应力路径为图中A点到C点，并且在C点达到破坏状态. 对于修正剑桥模型（图2a），其弹性区范围（从A点到B点）很大，而塑性区范围（从B点到C点）相对很小. 对于修正关口-太田模型（图2 b），其弹性区范围（从A点到B点）很小，而塑性区范围（从B点到C点）相对很大. 因此，我们不难判断修正剑桥模型的计算结果会比修正关口-太田模型的计算结果小，这也从理论上对修正剑桥模型的计算结果比真实值偏小，而修正关口-太田模型的计算结果比真实值偏大这一现象给出了合理解释.

图2 修正剑桥模型与修正关口-太田模型屈服轨迹的比较Fig.2 Comparison of yield locus between modified Cam-Clay model and modified Sekiguchi-Ohta model

修正剑桥模型弹性区范围偏大，修正关口-太田模型的塑性区范围偏大，为了克服两者的缺陷，本文构建了一种改进的模型，即在修正关口-太田模型的基础上将硬化轴再次旋转，将原模型的η0修正为η0/2，于是改进后的模型如下：

应力比参数

屈服函数

本文模型调整了屈服方程和硬化轴，其在p-q平面上的屈服面的形状为关于η0/2 对称的椭圆，如图3所示.

图3 本文模型的屈服轨迹Fig.3 Yield locus of the model in this paper

2.2 数值试验验证

采用本文所提出的弹塑性模型对本文2.1 小节中的算例再次进行计算，算例尺寸、计算参数及加载路径均相同. 同时，将不同荷载下不同弹塑性模型计算所得的最大沉降进行对比，结果如表2所示.

表2 不同荷载下采用不同模型计算的最大沉降Tab.2 Maximum settlements calculated by different models under different loads

第二级荷载作用下采用不同弹塑性模型计算所得的沉降等值线图如图4所示.

图4 第二级荷载作用下采用不同弹塑性模型计算得到的沉降等值线图（单位：mm）Fig.4 Settlement contour maps calculated by different elastic-plastic models under the second level load（unit：mm）

由图4可知，第二级荷载作用下采用几种弹塑性模型计算得到的沉降等值线的形态基本一致，仅在具体数值上存在差别. 由表2可知，在第一级荷载作用下，采用修正剑桥模型计算得到的最大沉降最小，采用关口-太田模型计算得到的最大沉降最大. 因为本文模型的弹性区范围比修正关口-太田模型的弹性区范围稍大，所以采用本文模型计算得到的最大沉降稍小. 在第二级荷载作用下，通过四种模型计算得到的最大沉降都显著增大，总体规律和第一级接近，但是在第二级荷载作用下，通过修正剑桥模型、修正关口-太田模型和本文模型计算得到的最大沉降都比较接近.

3 有限元强度折减稳定性分析

3.1 计算程序

采用河海大学岩土工程研究所研制的BCF二维固结有限元程序进行计算，利用该程序可得出位移、应力、孔压分布随时间的变化，可用于计算土工结构平面应变问题，如建筑物地基、土坝、路堤、挡土墙的计算等.

3.2 开挖边坡算例

开挖边坡形状及尺寸如图5所示，坡高为10 m，原始坡比为1∶2.5，开挖完成竣工期坡比为1∶1. 为了模拟开挖施工的具体工况，对该简单边坡进行三级开挖，荷载分四级，第一级荷载为初始状态，剩下的三级荷载分别对应分级开挖的相应一级.

图5 开挖边坡形状及尺寸Fig.5 Shape and size of excavation slope

开挖边坡施工前和竣工后的网格划分如图6所示，开挖边坡的基本参数见表3. 开挖边坡施工前的网格共有664 个单元、716 个节点，开挖边坡竣工后的网格共有600 个单元、656 个节点，每个单元采用四边形单元，控制网格尺寸大小使得相对单元密度达到每10 m2不少于3个节点；并且L坡脚到左端边界=1.5H坡高，L坡顶到右端边界=2.5H坡高，且H上下边界≥2H坡高，底部固定端约束，左右两侧均为水平向约束［17］.

图6 开挖边坡施工前及竣工后的网格划分Fig.6 Grid division of excavated slope before construction and after completion

表3 开挖边坡的基本参数Tab.3 Basic parameters of excavated slope

3.3 不同本构模型对边坡稳定性及边坡变形计算结果的对比分析

在有限元强度折减法中，边坡稳定性安全系数定义为岩土体实际抗剪强度与临界破坏时折减后抗剪强度的比值，即以达到临界破坏状态时的强度折减系数Fk作为边坡稳定性安全系数Fs. 根据特征点位移突变判据［18-20］，采用不同模型计算开挖边坡的强度折减系数与坡顶点水平位移、竖向位移的关系，结果如图7所示. 图8 为开挖边坡竣工后根据极限平衡法计算的结果，结果显示边坡的稳定性安全系数Fs为1.30，与图7中通过四种模型计算得到的强度折减系数拐点出现的值较接近，说明采用不同本构模型及方法对边坡有限元强度折减稳定性的计算结果是一致的. 因为不同模型在p-q平面上的屈服轨迹不同，所以计算得到的边坡变形也会有所不同. 通过不同弹塑性模型计算所得的坡顶点位移如表4所示. 本文模型调整了卸荷应力路径下的弹性区范围，塑性变形区范围增大且考虑到了开挖卸荷工况的影响，故采用本文模型计算所得的坡体滑动的临界位移也有所提高.

图7 通过不同模型计算所得的开挖边坡有限元强度折减系数与坡顶点位移的关系Fig.7 The relationship between the finite element strength reduction coefficient of excavated slope and the displacement of slope apex by using different models

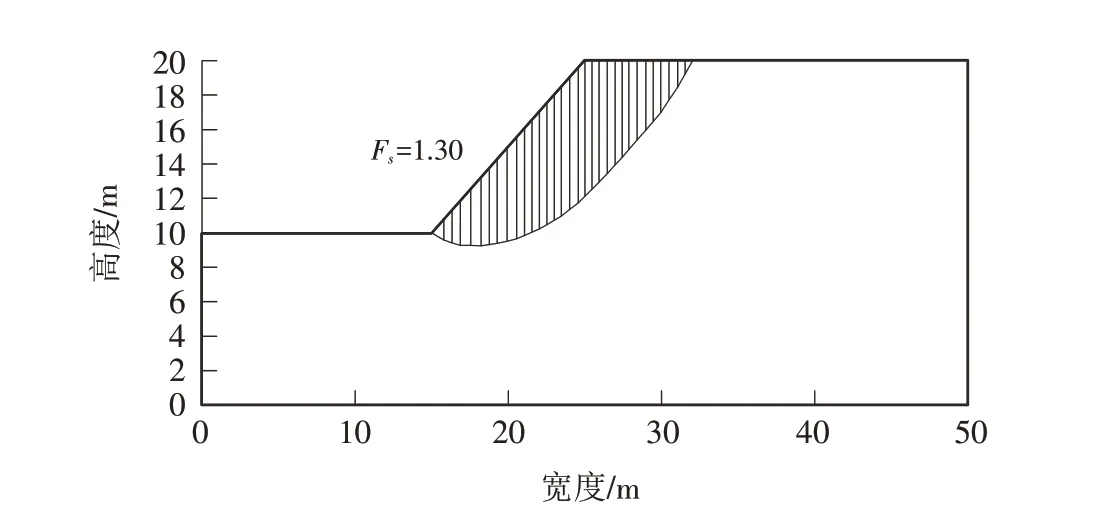
图8 开挖边坡竣工后采用极限平衡法计算得到的边坡稳定性安全系数Fig.8 Slope stability safety factor calculated by limit equilibrium method after completion of excavated slope

表4 采用不同模型计算所得的坡顶点位移Tab.4 Displacement of slope apex calculated by different models

4 考虑开挖边坡施工过程的有限元强度折减稳定性分析

在实际工程中，土质边坡伴随着开挖卸荷的过程，土体内部应力会重新分布，局部应力会集中或强度降低，土体会产生剪切破坏. 有限元强度折减法是通过对土体强度参数加以人为折减以进入极限平衡状态下土体所对应的状态，然后再通过该方法计算得到土体的应力变形，所以最终也只能根据该方法的计算结果给出可供参考的相应条件下的土体变形信息，并不能给出开挖边坡施工过程中土体的真实应力变形和边坡的稳定性安全系数的变化规律. 鉴于此，通过有限元强度折减法对开挖边坡施工过程中分级开挖对边坡稳定性与变形的影响进行了模拟分析.

4.1 分级开挖卸荷有限元计算

基于本文模型，采用有限元强度折减法对原始边坡模拟三级开挖，分步进行边坡稳定性计算与变形分析，开挖边坡形状及尺寸如图5所示，各级开挖边坡的网格划分如图9所示.

图9 原始边坡及各级开挖边坡的网格划分图Fig.9 Grid division diagram of original slope and excavated slope at all levels

图10为边坡三级开挖的有限元强度折减系数与坡顶点水平位移、竖向位移的关系图. 结果显示，随着开挖深度的增加，施工期边坡坡度由1∶2.5增加到1∶1，边坡的稳定性安全系数由最先的1.55降低到1.29. 而在三级开挖过程中，边坡特征点位移没有发生较大变化. 与此同时，同一强度折减系数下，每一级开挖完成后的坡顶点的水平位移和竖向位移均增大（图10）. 当边坡开挖完成后，边坡的稳定性安全系数为1.29，仍能满足边坡设计的要求，对应的坡顶点水平位移、竖向位移见表5.

图10 开挖边坡有限元强度折减系数与坡顶点位移关系图Fig.10 Relationship between finite element strength reduction factor of excavation slope and slope vertex displacement

表5 采用不同方法计算所得的各级开挖边坡的稳定性安全系数Tab.5 Stability safety factors of excavation slopes at all levels calculated by different methods

总之，在对实际开挖工程进行有限元计算分析时，要考虑到土体实际的施工过程，这对于准确地预测开挖工程中土体的变形及边坡稳定性是十分必要的.

4.2 极限平衡法的平行验证

图11 为边坡开挖施工前和分级开挖各阶段运用GEO-SLOPE 软件、Morgenstern-Price 法自动搜索的滑面，结果显示其与通过有限元强度折减法计算所得到的稳定性安全系数较为一致. 同时由表5可知，通过有限元强度折减法和极限平衡法计算得到的各级开挖边坡的稳定性安全系数相差不大，说明有限元强度折减方法可以应用到边坡开挖的稳定性计算中.

图11 采用极限平衡法计算所得的各级开挖边坡的稳定性安全系数Fig.11 Stability safety factors of excavated slopes at all levels obtained by limit equilibrium method

5 结论与展望

5.1 结论

采用有限元强度折减法对开挖边坡的稳定性进行了分析，并与采用不同剑桥系列本构模型计算得到的边坡稳定性安全系数与位移进行了对比，得到以下结论：

1）采用极限平衡法和不同本构模型计算所得的边坡稳定性安全系数具有一致性，表明如果采用的强度参数一致，那么采用不同本构模型对边坡稳定性的评估效果是统一的，由此验证了有限元强度折减法的有效性和合理性.

2）因为不同模型对开挖边坡土体单元的应力应变描述不同，所以采用不同模型计算得到的边坡特征点位移也不同. 采用变形量为失稳判据，需选用能反映真实开挖应力路径的本构模型，这样才能计算得到反映真实施工过程的土体变形.

3）开挖卸荷施工过程中，边坡稳定性逐渐降低，每一级开挖完成后坡顶点的水平位移、竖向位移均随之增大. 实际工程中，可以结合稳定性计算和施工变形观测，对开挖边坡的稳定性进行事前预测、实时预警，并采取相应处置措施，以保证边坡安全.

5.2 展望

目前的研究主要是对简单均质土质边坡在开挖卸荷工况下的有限元强度折减稳定性进行分析，通过简单的特征点位移量和强度折减系数之间的关系来建立变形量失稳判据，但不同边坡具有不同的几何尺寸、土层分布等参数，且不同边坡的复杂程度不同，因此下一步研究中需要建立能适用于不同边坡几何、物理参数的归一化变形量失稳判据.