基于Ansoft的电机械制动用电机仿真方法

陈茂林，曹家伟

（同济大学机械与能源工程学院，上海201804）

电机械制动系统是新一代的轨道车辆制动系统［1-2］。传统轨道车辆制动系统大多为空气制动系统，部分城轨低地板列车采用液压制动系统［3］。电机械摩擦制动系统采用电机作为动力源，相较于前两种制动系统，其有着系统响应快、结构紧凑、系统轻量化、清洁环保、便于智能诊断和故障检测等优点［4］。

电机械制动系统是一种机电一体化的伺服系统［5］。驱动电机是核心动力元件，对整个系统的性能影响很大，而市面上已有的产品难以满足电机械制动系统对大力矩、小尺寸的要求，因此，驱动电机往往需要特殊设计。与传统的制动系统类似，电机械制动系统完成制动也需要两个步骤：①空转消除间隙；②堵转提供夹紧力。驱动电机与一般电机不同，工作在两种情况下：①空转；②堵转。其中，在空转时要求能缩短制动响应时间，减少空走时间，在堵转时能提供稳定目标制动力。

通过以上分析可以知道，对于驱动电机的设计仿真，主要着力于空载和堵转两种情况。Ansoft maxwell 是一款强大的电磁有限元仿真软件，其中能通过rmxprt 磁路模块进行快速的电机有限元模型建立，为设计仿真工作提供很大便利。但在rmxprt 模块中，磁路计算只有空载和额定工况下的结果，不能得到电机堵转时的性能。在maxwe1l中，对于电机空载的仿真，通常将三相激励电流设置为0即可［6］。因为理想状态下空载时激励电压等于反电动势，使得绕组中电流为0。而对于工作在堵转工况的电机的电磁仿真并不常见，大部分对于堵转工况的仿真是为了研究电机的启动性能［7-9］。通过磁路计算的结果生成的有限元模型及参数，并不能直接仿真工作在堵转状态下的电机。本文通过对一套设计好的电机参数，进行了磁路计算、有限元空载计算及有限元额定工况计算，获得了电磁场性能；并介绍了两种不同修改激励的方式，近似模拟电机械制动用电机的堵转工况计算，为驱动电机的设计提供便利。

1 驱动电机基本组成及工作原理

电机械制动用电机拟采用方波驱动的三相无刷直流电机。电机本体主要组成为定子、转子和电机轴，定子上开槽镶嵌绕组，转子上表贴永磁体，采用内转子结构。

电机本体配上位置传感器、逻辑控制电路及功率开关等组成了电子换向装置，通过位置传感器的信号，在特定时间段给三相绕组通电流，产生旋转磁场，通过与转子上永磁体相互作用，使转子旋转，并产生力矩。现有驱动电机尺寸参数如表1所示。

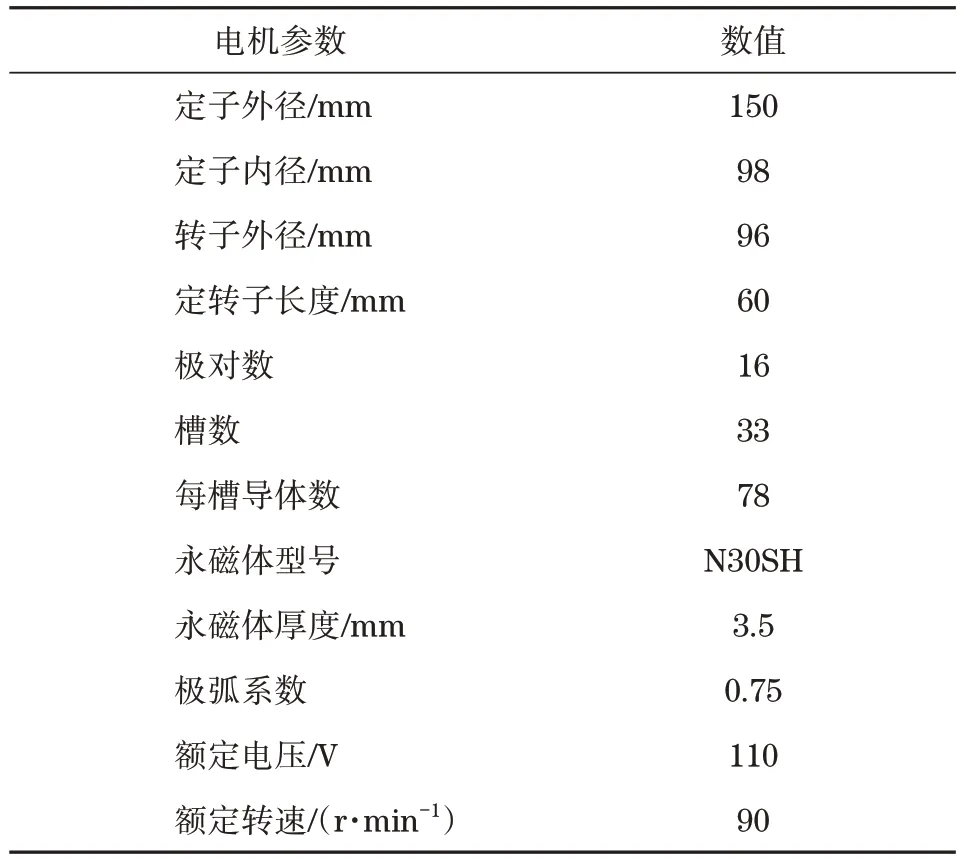
表1 电机参数Tab.1 Motor parameters

2 无刷直流电机方波驱动原理

无刷直流电机采用方波驱动，根据转子的位置，给对应绕组通电。在每个时刻，只有两相绕组导通，每相绕组导通电角度为120°［10］。在一个电周期内，有6 种不同的导通组合，因此又称为六步方波驱动。驱动电路示意图如图1所示。

图1 六步方波驱动电路［10］Fig.1 Six pulses square-wave drive circuit［10］

当霍尔传感器120°布置时，各绕组电流在1 个电周期内分布情况如图2所示。

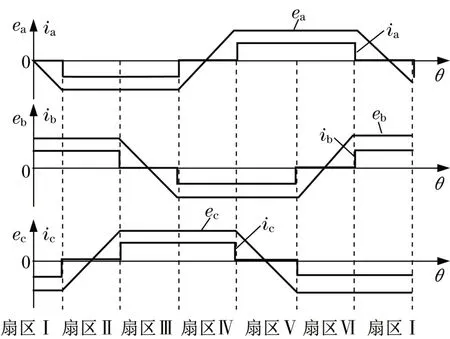
图2 绕组电流分布Fig.2 Distribution of winding current

可以看出，在无刷直流电机运行时，同时只有两相绕组导通，每相绕组导通时间为120°电角度。在一个电周期内有6 种不同的导通状态，每个状态持续60°电角度。

3 电机械制动用电机磁路计算

通过将电机参数输入进ansoft 的rmxprt 模块，对电机的性能进行快速的估算。Rmxpet 计算结果如表2所示。

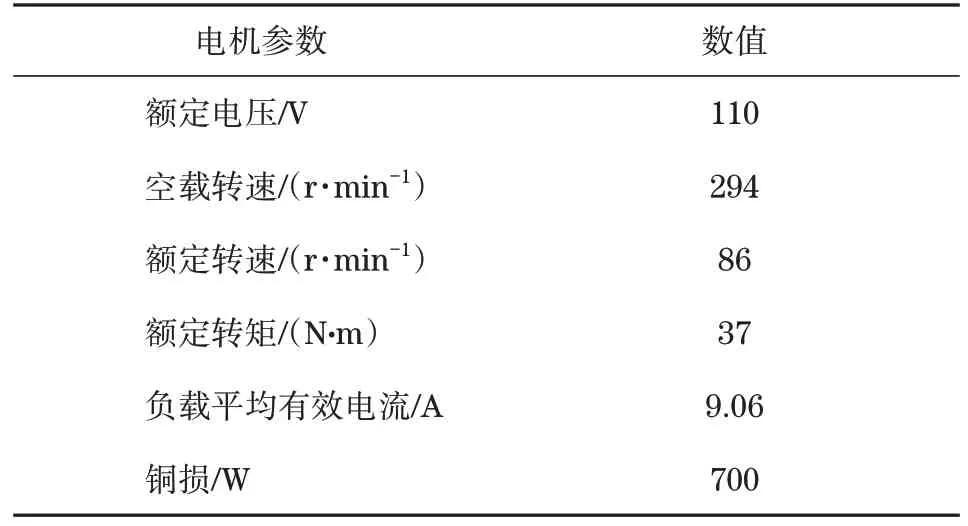
表2 磁路计算结果Tab.2 Calculation result of magnetic circuit

负载反电动势约为17.5 V，如图3所示。

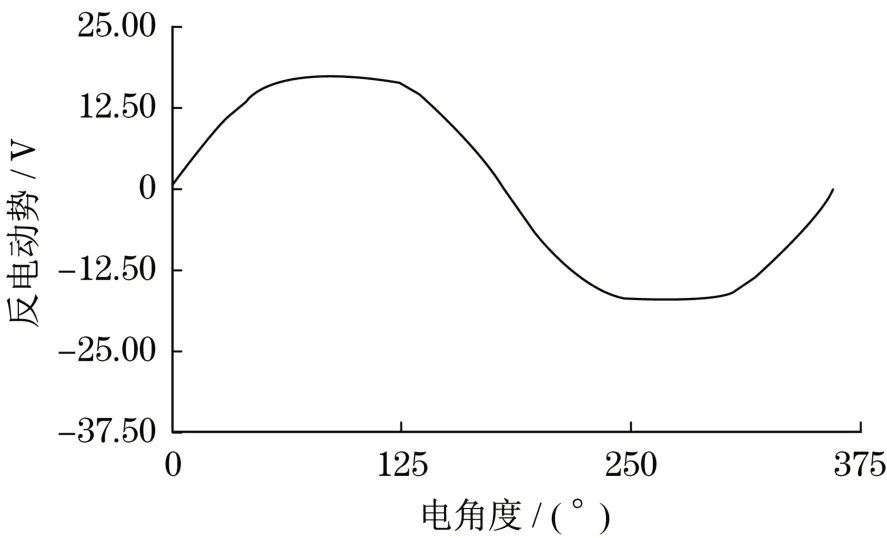
图3 反电势波形Fig.3 Waveform of back EMF

气隙磁密波形呈平顶梯形，约为0.75 T，如图4所示。

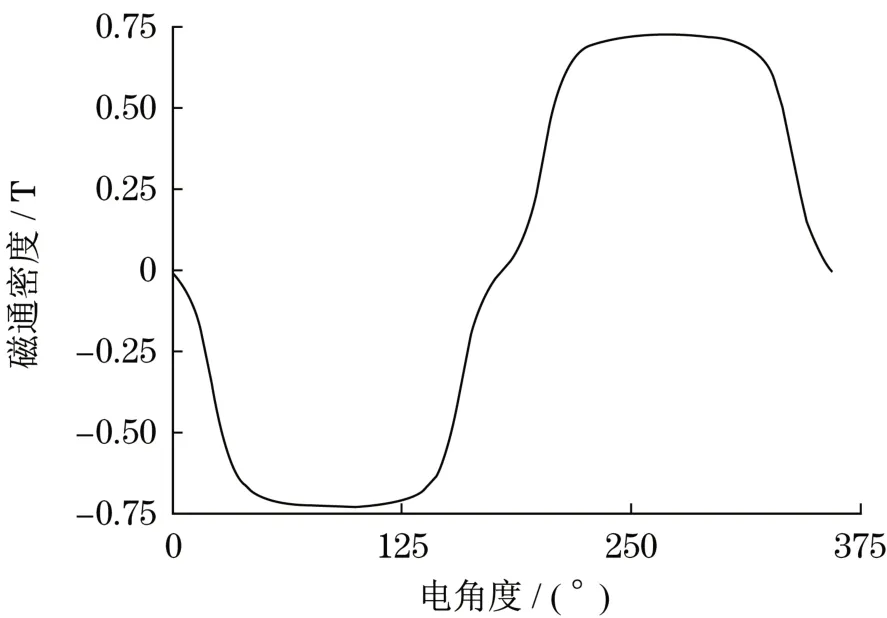
图4 气隙磁密波形Fig.4 Waveform of air gap magnetic density

4 电机械制动用电机空载及额定工况有限元计算

通过将rmxprt磁路计算结果导入maxwell2D，一键生成电机磁场全域有限元模型，如图5所示。

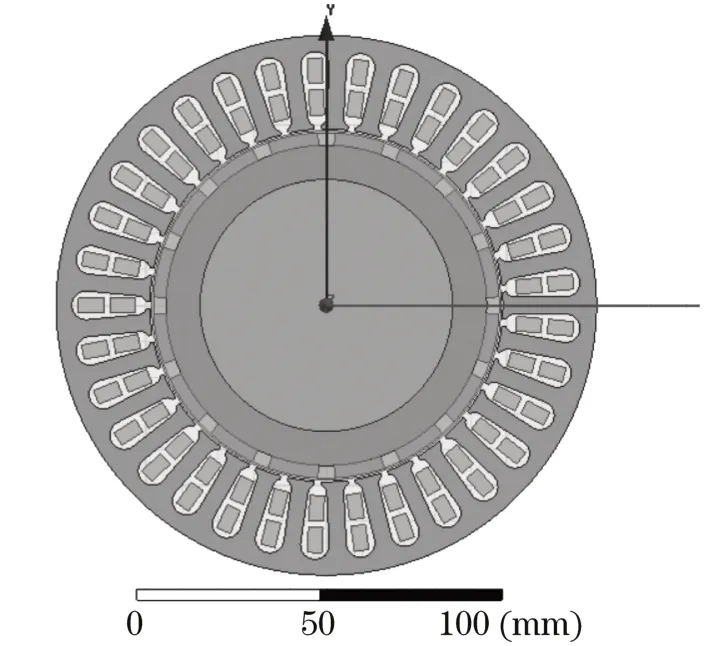
图5 电机有限元全域模型Fig.5 Complete finite element model of the motor

4.1 空载仿真计算

将三相激励设置为电流源CurrentA、CurrentB、CurrentC，均为0，在机械设置中，将转速设置为294 r/min，定子外圆磁矢位设置为0作为边界条件。仿真时间设置为0.18 s，步长为0.000 9 s。

电机空载磁场分布如图6 所示。当电机空载时，仅有永磁体提供磁通，磁场分布均匀。最高磁密为1.447 4 T，位于定子齿部且小于硅钢片饱和磁密，因此没有过饱和，磁路设计合理。

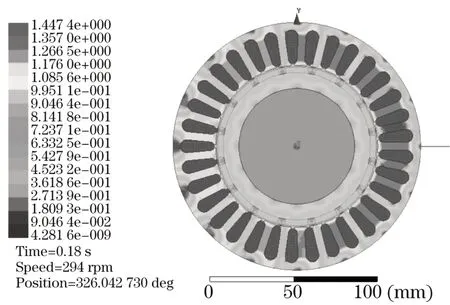
图6 空载磁密分布云图Fig.6 Cloud picture of magnetic density under noload conditions

4.2 额定工况仿真计算

电机在额定工况时，将三相激励设置为外电路，外电路在生成电机有限元模型时一并生成，如图7 所示。将转速设置为86 r/min，计算时间及步长不变，进行计算。

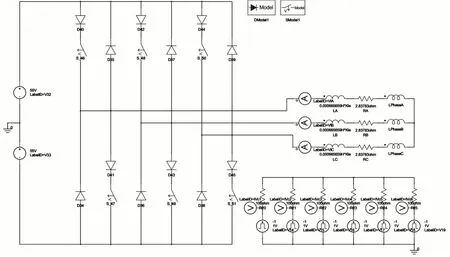
图7 外部驱动电路Fig.7 External drive circuit

电机输出转矩如图8 所示，平均转矩约为35 kN，转矩脉动约为14%。对于无刷直流电机，大部分转矩波动来源于换向时电流的滞后。

图8 额定工况转矩曲线Fig.8 Torque curve under rated conditions

电机单相铜损平均值约为370 W，如图9所示。

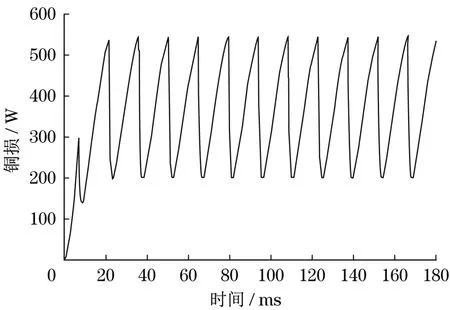
图9 单相铜损曲线Fig.9 Single-phase copper loss curve

5 电机械制动用电机堵转工况仿真计算

电机械制动用电机的实际工况是堵转状态。通过不同的改变激励的方法，可以模拟对驱动电机堵转工况的仿真计算。

若仅将仿真转速设置为0，采用外部电路驱动，计算结果如表3所示，与磁路计算相去甚远。

表3 转速为0的有限元仿真结果Tab.3 Finite element simulation results with zero speed

永磁直流电机的电压平衡方程为

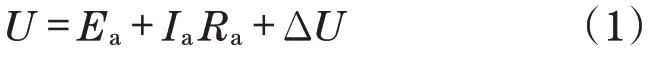
式中：U为输入电压，V；Ea为反电动势，V；Ra为电枢回路电阻，Ω；Ia为电枢电流，A；ΔU为驱动回路压降，V。

由上可知，在仿真计算时反电动势实际为0，而控制电路输入电压依旧为额定工况时的输入电压。因此实际作用在绕组上的电压将高于额定工况，最终导致仿真结果中绕组电流偏高，计算得到的力矩偏大，损耗偏大。

实际电机械制动系统的扭矩转速曲线如图10所示。图中，A点为空载工况，B点为额定工况。当转速继续降低时，通过电流闭环控制力矩保持不变，进入恒力矩工作区域，直至C点堵转工况。在磁路计算中，仅仅只有A点和B点的计算结果。D点为开环系统下的堵转工况，也就是直接将转速设置为0 所仿真计算的工况。而对于电机械制动用电机实际所需要仿真计算的工况为C点。

图10 转速-转矩曲线Fig.10 Speed-torque curve

5.1 电流源激励

电机械制动用电机实际堵转工况为C点，与B点力矩相同。

永磁电机电磁转矩计算公式为

式中：CT为转矩常数；Φ为每极气隙磁通，Wb。

对于一个电机模型，其转矩常数及每极气隙磁通不变，若要保持电磁转矩不变，只要保持电枢电流不变。因此，可以将激励设置为电流源，数值为额定工况下每相的稳定电流。

在磁路计算中得到平均有效电流为9.06 A。在转子旋转时，由于六步方波控制，每相电流导通时间理论只占2/3，实际由于提前换向，及绕组的电感性，每相电流取3/4为平均电流，即堵转时两项绕组电流为12.08 A。

根据转子初始位置，将A相绕组电流设置为0，B 相绕组电流设置为-12.08 A，C 相绕组设置为12.08 A，将电机转速设置为0，进行堵转工况仿真计算。

仿真结果如图11 和图12 所示，转矩为38.8 N•m，单相铜损为345 W，总铜损为690 W。此结果更接近于电流闭环的堵转工况，但是忽略了驱动电路的影响。

图11 堵转转矩曲线Fig.11 Torque curve under locked conditions

图12 单相铜损曲线Fig.12 Single-phase copper loss curve

5.2 外电路激励

由永磁直流电机的电压平衡方程可知，将外部驱动电路电源的数值改为为输入电压减去额定工况下的反电动势，理论上能模拟电机堵转工况。

在磁路计算中，相反电动势为17.5 V，则实际作用在绕组上的电压为110 V-35 V=75 V。将外部驱动电路串联直流电源都改为37.5 V，重新导入节点进行计算。

仿真计算结果如图13~图15 所示。力矩约为39.5 N•m，单相铜损为365.0 W，B、C 两相电流为12.5 A。力矩比额定工况磁路计算略高，同时损耗也更高。此仿真方法考虑了驱动电路的影响，同时也能得到各参数动态响应的过程。

图13 堵转转矩曲线Fig.13 Torque curve under locked conditions

图14 单相铜损曲线Fig.14 Single-phase copper loss curve

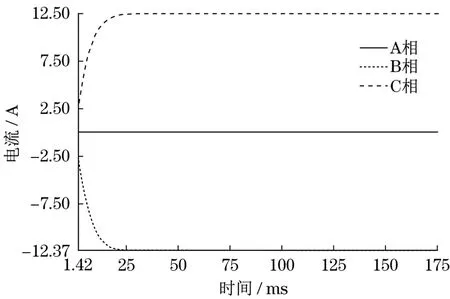
图15 三相绕组电流曲线Fig.15 Three-phase winding current

6 结语

本文通过ansoft 对现有一套电机械制动用电机参数进行了磁路计算，通过有限元空载仿真、有限元额定负载仿真及有限元堵转仿真，得到了电机的基本电磁性能及输出性能。本文提出了两种不同的模拟电机堵转工况仿真方法。通过与磁路计算额定工况计算结果的对比，使用电流源仿真结果力矩及铜损更接近，但对于输入电流的预估需要一定经验，同时由于忽略了绕组本身的一些属性，结果更接近于理想状态。通过修改外部电路输入电压，仿真结果力矩及铜损都偏高，但是仿真结果包含了驱动电路及绕组本身的影响，使结果更接近实际。