双向聚能非均布荷载作用下浅埋隧道动力响应
2021-12-22胡文韬胡继民陶彪耿大新刘鑫磊徐长节
胡文韬,胡继民,陶彪,耿大新,刘鑫磊,徐长节,2
(1. 华东交通大学江西省地下空间技术开发工程研究中心,江西南昌 330013;2. 华东交通大学江西省岩土工程研究所,江西南昌 330013;3. 中国铁路南昌局集团有限公司南昌高铁基础设施段,江西南昌 330100)
随着我国城市化进程加快,城市发展与土地资源短缺的矛盾日益突出。城市人口的不断增加,工业化进程的加速,汽车持有量的提高,带来了一系列空间需求,对地下空间的合理开发利用是解决这些矛盾的重要途径。然而在运营的公路隧道内存在因交通事故而导致爆炸的安全隐患;正在施工建设的隧道,在已修建好的隧道区段内,由于安全隐患(瓦斯、不安全施工)而导致的爆炸,交通隧道、综合管廊等地下空间结构受到爆炸时会引发隧道衬砌结构及围岩的破坏。因此,研究爆炸荷载对隧道的动响应问题对科学有效地指导隧道结构施工、减少人员伤亡、财产损失具有重大意义。针对地下空间动力响应的理论研究方面,SENJUNTICHAI 等[1]基于biot 理论研究突加荷载、跃阶荷载和三角脉冲荷载下全空间多孔弹性介质的圆柱形洞室的动力响应,得到了响应的解析解,并通过Laplace 数值逆变换,得到了时域下的数值解;ZAKOUT等[2]通过残余变量法,得到了在弹性全空间介质下有衬砌和无衬砌圆柱形洞室的动力响应结果;FELDGUN 等[3]通过有限差分法,研究了深埋管线内部受到爆炸冲击荷载下管线内部及周围土体的动力响应;MENG 等[4-5]提出一种受到内源荷载下圆柱衬砌瞬态动力响应的解析解,研究了多孔弹性和弹性土体中土体泊松比、土体动态剪切模量、衬砌动态剪切模量以及衬砌厚度对衬砌和土体的动力响应影响。耿大新等[6-7]研究了内源非均布瞬态荷载下全空间洞室波动特性以及剪切模量等因素对应力位移场在径向和环向上分布特征的影响。蔡袁强等[8]通过将爆炸荷载简化为三段阶梯形衰减形式,衬砌采用Flügge 壳体理论,研究了饱和土体的排水条件对隧道及其衬砌结构的位移和应力影响并研究饱和土体参数和衬砌结构参数以及饱和土体中排水条件对衬砌空腔的影响。对于浅埋隧道动力响应的研究,COSKUN 等[9]分析了弹性半空间内圆柱形洞室受到均布荷载下的动力响应,研究了浅埋情况下洞室内波数和隧道埋深对位移和应力响应的影响。LI等[10-14]通过引入大圆弧假定,采用Fourier 变换和波函数展开法研究了P 波、SV 波和Rayleigh 波作用下弹性介质中浅埋圆柱形衬砌的动应力集中问题。WANG等[15]也将半空间直线边界近似由大半径的凸弧表示。根据Graf 加法定理,将直角坐标系中的一般解转换为极坐标系中的一般解。根据边界条件推导了土和衬砌的位移和应力以及土的孔隙压力在拉普拉斯变换域中的解。本文基于文献[6-7],瞬态荷载发生时,因外部约束的存在荷载向极轴处汇聚,径向应力差导致沿径向同一圆环内的位移不均,进而产生剪应力,圆形洞室施加的瞬态荷载到达最大值后又迅速衰减至0,因此将爆破荷载理想化为双向聚能的非均布瞬态荷载并作用在浅埋衬砌隧道边界上。根据弹性动力学理论和Hamilton 壳体理论得到围岩运动方程和衬砌运动方程,采用波函数展开法和Graf 坐标变换法,并利用洞室与荷载连续边界条件以及爆炸初始和爆炸后地面零应力边界条件,求解出浅埋衬砌隧道中双向聚能的非均布瞬态荷载响应的解析解,分析增加爆破能量的同时,如何通过调整爆破角度以及其他爆破参数减少地面扰动。
1 半空间洞室模型及波场方程求解
计算模型假定在弹性土体中存在一个深度为H,半径为a的无限长圆形洞室,在洞室中心处受到径向非均匀荷载f(θ,t)=f(θ)·s(t),f(θ)为荷载分布特征函数,随θ变化所分布的荷载集度不同。由于隧道沿纵向的应变远远小于隧道横向应变,因此忽略洞室纵向爆炸动响应,将模型简化为平面应变问题。计算模型如图1 所示,设定2 个平面极坐标,洞室内部中心处极坐标O1(r1,θ1),同时定义地表处为无限长大圆弧,圆弧半径Rg,圆弧中心处极坐标O2(r2,θ2)。
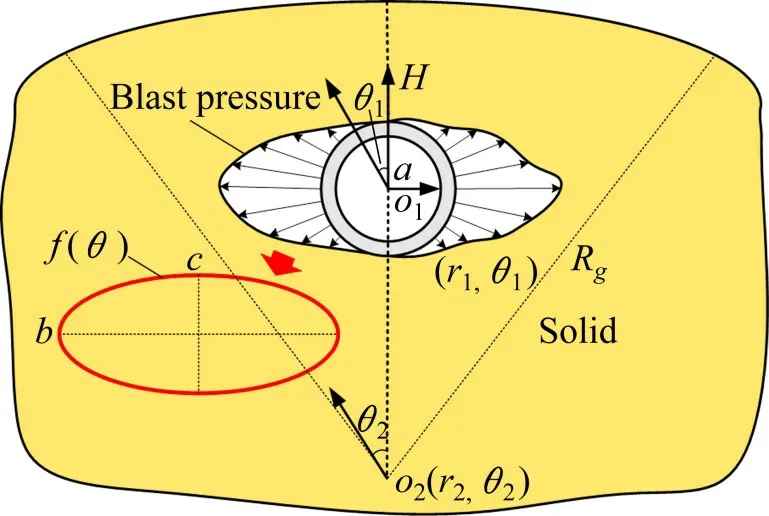
图1 双向聚能荷载浅埋隧道模型Fig.1 Model of shallow buried tunnel with bidirectional shaped charge


图2 三角脉冲荷载Fig.2 Triangular pulse load
将土体结构视为理想弹性单相介质,忽略体力,此时的土体运动方程及平衡方程的张量形式表达如下:
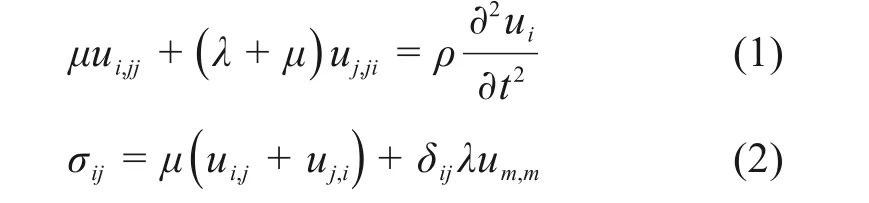
式中:ui为土体位移;σij为土体应力张量;λ,μ分别为土体的lame 常数;ρ为土体密度;δij为Kronecker参数,当i≠j时δij= 0,i=j时δij= 1。
时域下的平衡方程通过下列Laplace 变换可消除式(1)的时间导数项:

通过Laplace 变换,将时域下位移表达ui转化为复频域下表达uˉi,通过引入标量势函数φ和矢量势函数ψ,土体位移ui可用势函数张量表达为

式中:φ和ψ分别为土体的标量势函数和矢量势函数,将式(4)代入式(1)得到Helmholtz方程如下:

浅埋隧道条件下,考虑聚能分布荷载环向对称性,对方程(6)的势函数进行分离变量求解得到下列势函数形式。

浅埋隧道通过引入半空间大圆弧假设,如图3所示,将隧道洞室坐标系O1(r1,θ1)地面边界处应力位移条件通过graf加法定理转变为大圆弧坐标系O2(r2,θ2)下的表达:
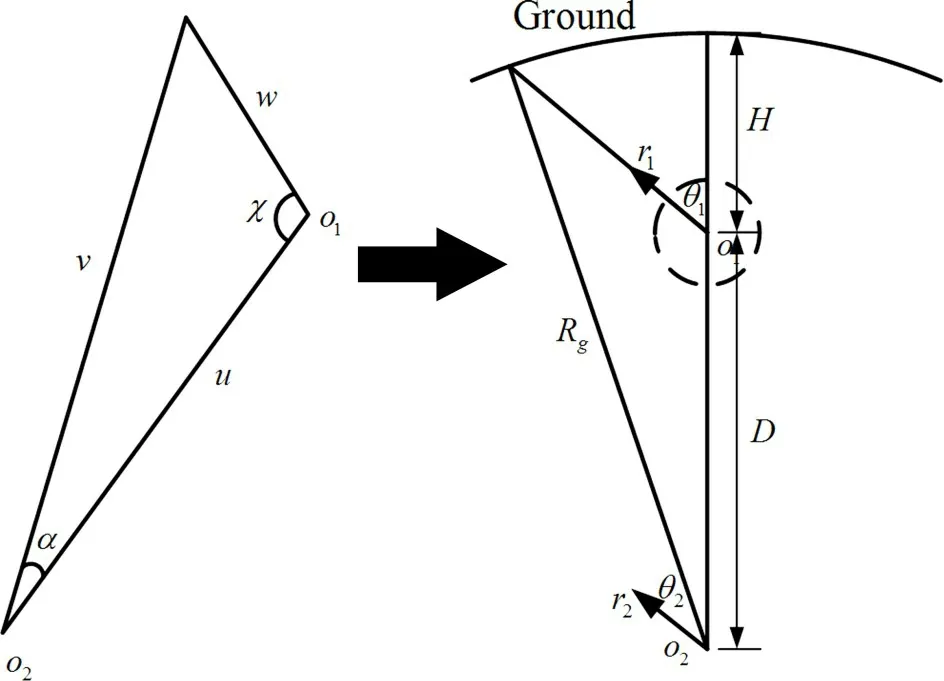
图3 graf坐标变换Fig.3 Graf coordinate transformation
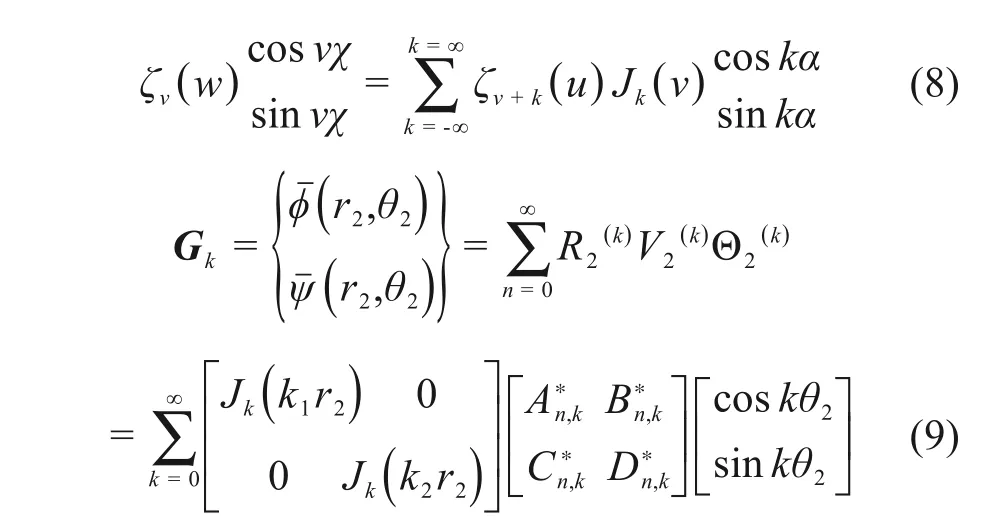

2 衬砌控制方程及边界条件求解
假设衬砌和周围土体协调变形,采用薄壁壳体模拟隧道衬砌,不考虑衬砌扭矩并进行Laplace变换后得到衬砌运动方程。

假定隧道计算模型衬砌与围岩土体满足连续性条件,在衬砌-土体接触面上具有应力位移相容性,得到边界条件如下:
隧道衬砌外表与围岩接触面边界条件为,当r1=a+h时,
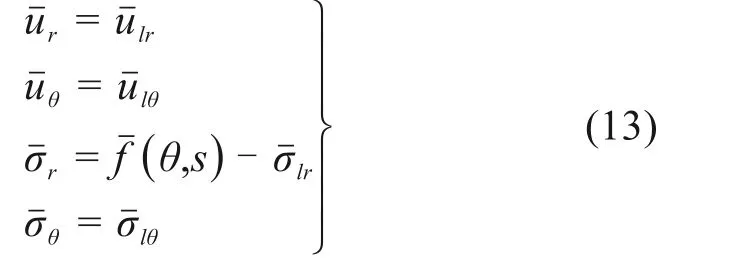
在大圆弧自由表面处边界条件为,当r2=Rg时,

3 数值计算及算例分析
本文求得隧道衬砌及围岩频域下的动响应表达,对于此类频域下的表达采用Laplace 数值逆变换比较困难,故采用Durbin[16]数值逆变换,其表达如下:

根据式(19)确定NUSM的计算区间:
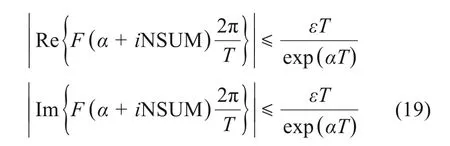
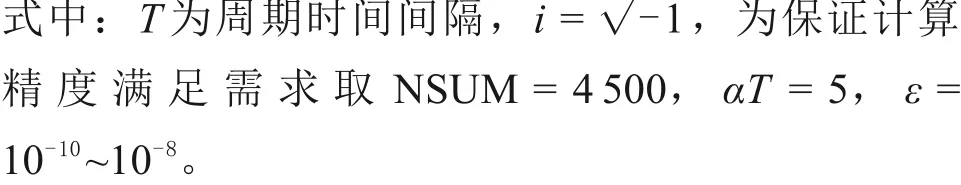
3.1 算例分析
为研究隧道埋深、衬砌厚度,浅埋环向角度和荷载集中集度对隧道动响应的影响,算例基本计算参数如表1所示。
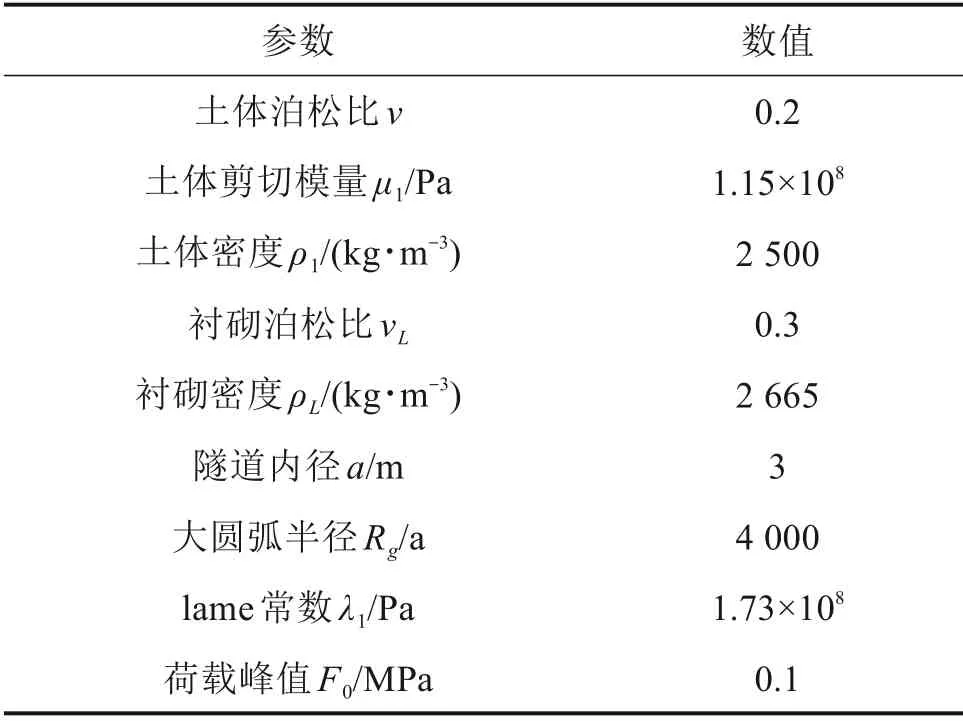
表1 基本计算参数Table 1 Basic calculation parameters
1) 时域下隧道不同位置上的波动
图4 表示在埋深为4 倍隧道内径的隧道中,衬砌-土体作用边界处不同角度上的波动响应,分别取隧道底部A点,隧道右侧面B点,隧道拱腰C点和隧道顶部D点进行分析。由图4 中的4 幅图对比可知,隧道的径向位移图4(b)和径向应力图4(d)响应峰值发生在隧道拱顶处,隧道的环向位移图4(a)和环向应力图4(c)响应峰值发生在隧道拱腰处,并且隧道顶部和底部响应的方向相反,并且响应趋势都趋于一致,随时间推移,响应逐渐衰弱;由图4(a)可知,由于隧道对称性和荷载对称性,隧道顶点、侧面点以及底部的环向位移均为0。
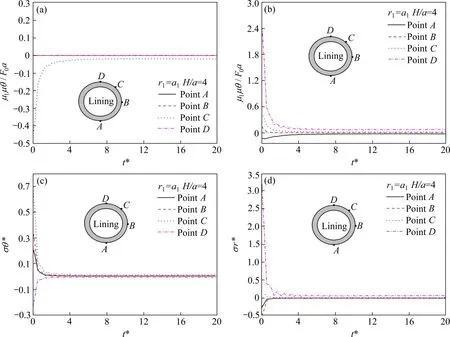
图4 隧道底部(A)、右侧(B)、拱腰(C)和拱顶(D)位置的环向位移响应曲线Fig.4 Circumferential displacement response curves
2) 峰值荷载时刻不同埋深下隧道波动响应
图5 表示当荷载达到峰值时,在4 倍、6 倍以及8 倍隧道内径的土体响应沿隧道环向变化曲线。将图5(a)、5(b)与图5(c)、5(d)对比分析可知,位移响应幅值较大,并且随着隧道埋深的增加,位移响应幅值先增大后减小。因为随着埋深的增加,爆炸入射波与地表反射的前期爆炸波波峰干涉,使得幅值减小,并且这种干涉效应对幅值影响在不同角度所呈现出来的性质也不同。通过径向位移(图5(b))各角度幅值变化能明显看出,在90°时幅值时先增后减,而在270°时却呈现先减后增。这说明在隧道顶部入射波和地面反射波波峰和波峰相遇,使得幅值先增后减,而在隧道底部,因为波程差的原因,使得此处是波峰和波谷相遇,使得幅值先减后增。此外在应力场图5(c)和5(d)中,隧道两侧响应随着深度增加应力幅值变化较小,而在隧道顶部和底部受入射波和反射波叠加效应影响,产生的幅值变化较大。

图5 峰值荷载时刻不同埋深下的环向位移Fig.5 Response curves of circumferential displacement
3) 峰值荷载时刻不同衬砌厚度下隧道波动响应
图6表示当荷载达到峰值时,在不同衬砌厚度条件下土体响应沿隧道环向变化曲线,根据实际工程要求选取衬砌厚度分别为15,30和45 cm。对图6 中4 幅图进行分析可知,随着隧道衬砌厚度的增加,整个隧道的动力响应幅值均减小,但是动力响应幅值减小并不明显,这主要是衬砌厚度变化范围较小所导致的。由图6(a)及图6(b)可知,随着隧道衬砌厚度的增加,隧道两侧及底部的环向位移响应幅值变化较小,顶部较为显著,整个隧道径向位移幅值变化不明显。由图6(c)可知,隧道环向应力在隧道130°和50°位置处达到极值,拱底环向应力响应在隧道底部随着隧道衬砌厚度的增加隧道响应的幅值均有明显减小,径向应力在隧道顶部处响应变化幅值最大。因此隧道衬砌厚度设计时,单纯增加衬砌厚度对隧道防爆隔振等级加强效果并不显著,可以在设计时考虑响应极值处进行衬砌加厚。
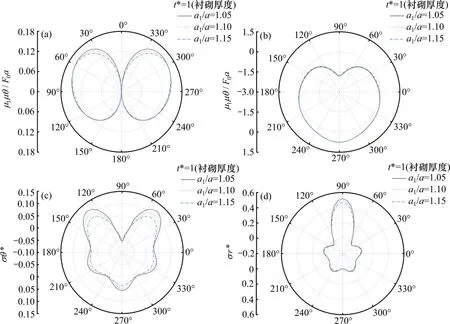
图6 峰值荷载时刻不同衬砌厚度下的环向位移Fig.6 Response curves of circumferential displacement
4) 峰值荷载时刻不同荷载集度下隧道波动响应
图7表示当荷载达到峰值时,在不同荷载分布集度下隧道周身土体的环向动响应变化曲线。由图7(a)和图7(b)可知,随着荷载集度的增大,在环向位移场上分别在顶部和在底部附近出现位移极值点,由于顶点和底部处为环向应力中值点,在此处环向应力为0,瞬态荷载向隧道两侧集中,使得隧道上部和底部附近出现较大的环向位移。因为隧道埋深较浅,内源振动导致隧道上浮,使得上部径向位移增大,下部径向位移减小。而随着荷载集度的增大,应力响应在隧道顶部减小,环向应力场在底部增大。因此,在浅埋隧道防爆抗震设计中,因优先考虑离地表较近处的土体的位移和应力。
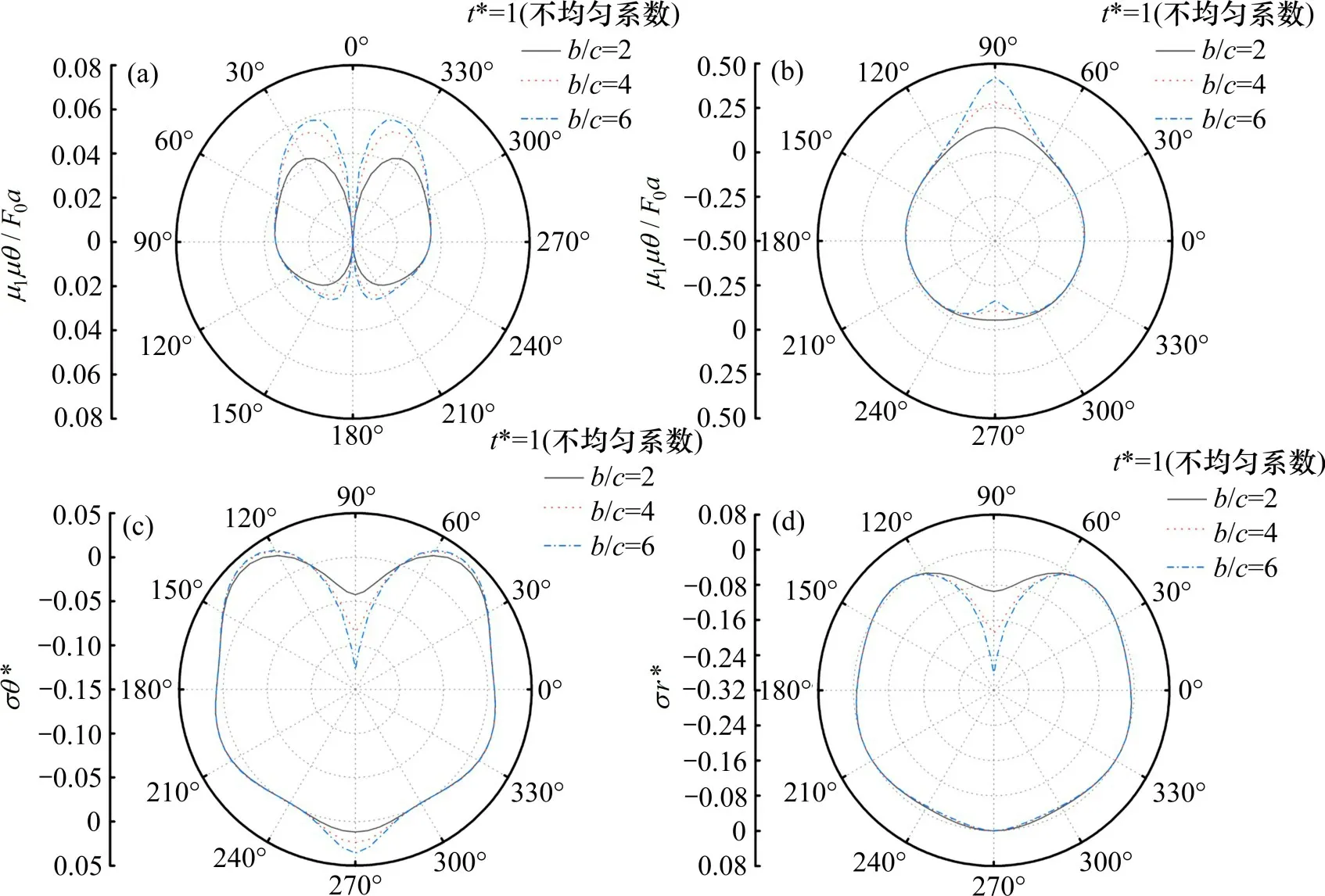
图7 峰值荷载时刻不同集度参数下的环向位移Fig.7 Response curves of circumferential displacement
4 结论
1) 浅埋隧道中,不同角度下的起始响应幅值不同,响应峰值发生在隧道顶部,位移和应力响应趋势相似,随时间推移,响应逐渐衰减。
2) 不同埋深下位移场和应力场由于爆炸入射波与反射波的相位差异,所产生的干涉效应不同,使得波动幅值影响在不同角度呈现出不同的性质,隧道顶部和底部响应幅值变化较为显著,环向位移随深度增加响应先增后减,径向位移响应顶部先增后减,在底部先减后增。
3) 衬砌的厚度增加使得响应的幅值减小,响应在两侧幅值变化较小,顶部和底部较为显著,并且随着厚度增加,对响应幅值的减小出现疲态,因此,衬砌厚度增加对响应幅值减小的增益程度有限。
4) 随着荷载集度增大,环向位移场上分别在顶部和在底部附近出现位移极值点,内源振动导致隧道上浮,使得顶部径向位移增大,底部径向位移减小,应力响应在隧道顶部减小,环向应力场在底部增大。
