学科核心素养视角下中学生数学学科能力水平状况与分析

刘一飞，黄文吉

（1.仁川大学，首尔仁川；2.榆树市第一高级中学吉林长春130024）

随着大数据时代的到来，数学核心素养成为学生核心素养发展的重要内容之一。有学者认为，传统“双基”（基础知识、基本技能）的数学教育使人们难以应付当今复杂的工作环境。［1］因此，培养学生数学核心素养是适应时代发展、社会进步的迫切需求。

一、问题的提出

数学核心素养是数学学习者在学习数学或学习数学某一个领域所应达成的综合性能力。［2］学生数学学科能力的培养是发展学生数学核心素养的关键。有学者指出，学科核心能力是学生通过学科学习形成的并且体现在各学科学习中的基本的、关键的、主要的能力，是学科独有的素养性能力，也是最能体现学科性质的关键的学科能力。［3］为此，在中学数学教育中，培养学生的数学学科能力是促进核心素养目标落实的重要途径之一。我国县（市）所辖地区学生数量庞大，为实现我国基础教育优质、均衡发展，势必要重视县域基础教育质量。由于数学学科能力是学生发展数学核心素养的一个重要方面，因此本文对2020 年吉林省C 市基础教育质量监测数据进行了二次分析，以数学学科能力为突破点，展开县域中学生数学学科能力水平及城乡差异状况的研究。

二、研究设计与方法

《数学课标2011 版》中明确指出：“在数学课程中，应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想”。［4］C 市八年级基础教育质量监测的测评工具则以《数学课标2011版》为依据，以查考学生数学学科核心素养为向导，通过内容领域、认知维度、学科能力这几方面来考察学生数学学业水平状况。其中，数学学科能力主要包括概念理解、运算技能、几何直观、推理能力四个维度。本研究数据分析主要采用二次分析方法。二次分析是对他人搜集整理的资料进行再分析。［5］Y 县2020 年基础教育质量监测共有39 所中学（包含8358 名八年级学生）参加了测评，相较其他地区所占数量最多、最具代表性。因此，本文对C 市数学学业质量监测数据进行了重整与二次分析。并确定了以下数据分析维度：首先，学科能力维度。从概念理解、运算技能、几何直观、推理能力四个维度考察学生数学学科能力发展状况；其次，城乡维度。为了更加细致地了解Y 县中学生数学学科能力水平，又将Y 县学校依据学校所在地区的行政划分，分为县城学校和乡镇学校两类。

三、结果与分析

（一）学科核心素养维度下县域中学生数学学科能力水平分析

1.Y县中学生数学学科能力水平总体分析

通过数据分析结果可以看出，Y 县中学生数学学科能力的总体均值为69.01，标准差为28.02。其中，在概念理解、运算技能、几何直观和推理能力维度上的均值分别为30.65、25.29、6.61、6.46；各学科能力维度得分率分别为0.74、0.61、0.39、0.32。Y 县中学生在概念理解维度的表现最好，其次是运算技能维度，均高于平均学科能力水平。而几何直观维度的能力水平偏低一些，推理能力表现相对较差，远低于平均水平。

由于学生推理能力维度得分率相较其他能力得分率较低，为探寻其原因笔者对涉及推理能力的试题做了进一步分析。在本次测评工具中主要考察学生推理能力的题目有第9 题、15 题、19 题等。分析发现19（2）题和15 题得分率最低，分别有78.1%和88%的学生完全回答错误。第15题主要考察学生运用和分析的能力，考察学生理解正方形和菱形的有关概念等，并能够运用勾股定理进行计算。该题目属于水平2，在该题目上学生的错误率高达88%，说明Y 县中学生化繁为简并理解化简后各部分之间联系的能力相对较弱；第19题共分为两小题。其中，第一小题考察学生的运算技能；第二小题则主要考察学生运用符号表示数与变化规律，体验数学思考中从特殊到一般规律的推理过程，Y 县中学生在该小题上的得分率较低。19（2）题属于水平3，在该题目上学生的错误率为78.1%，该题是较高水平的认知学习结果，该题得分率不理想主要由于学生综合运用多方面知识进行判断、评价能力较弱。

2.Y县中学生数学学科能力的具体表现分析

本研究再将每个数学学科能力应该达到的认知目标进行分类，形成每个学科能力的具体表现，每一种表现对应一种水平，其中水平1 为记忆与描述，水平2 为应用与分析，水平3 为综合与评价，从而进一步了解Y 县中学生在各能力维度上的具体表现及差异状况（见图1）。

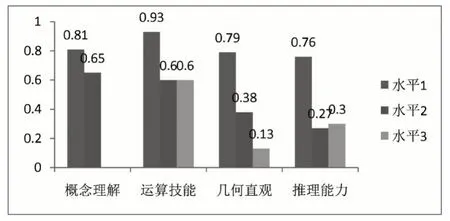
图1 Y县中学生数学学科能力中各难度水平的得分率

由图1 可以看出，在水平1 上，Y 县中学生在运算技能方面表现最好，得分率为0.93，远高于其他能力维度；而学生推理能力方面表现较差，得分率仅为0.76。在水平2 上，Y 县中学生在概念理解方面得分率最高，为0.65；推理能力方面表现较差，得分率为0.27。在水平3 上，Y 县初中学生在运算技能方面表现最佳，得分率为0.6，远高于其他学科能力；而几何直观方面则表现较差，得分率仅为0.13。

（二）城乡维度下中学生数学学科能力水平分析

1.Y 县城乡中学生数学学科能力水平总体差异状况分析

本文将数据分为县城和乡镇两类地区进行分析，考察这两类地区中学生数学学科能力水平状况，见表1。可以看出，县城中学生数学学科能力总分均值为70.13，乡镇学生数学学科能力总分均值为66.40，Y 县的县城中学生的数学学科能力总体水平要高于乡镇中学生。具体来看，在概念理解、运算技能和推理能力维度，县城中学生数学学科能力表现要好于乡镇的学生；而在几何直观维度，乡镇学生的分数均值为6.91，县城学生的分数均值为6.48，乡镇中学生数学学科能力表现要好于县城的学生。

表1 Y县城乡中学生数学学科能力水平均值描述表

通过独立样本T检验能够比较县城和乡镇两类地区中学生数学学科能力水平是否存在显著差异。通过分析发现，县城和乡镇两类地区中学生数学学科能力总体水平状况存在显著差异（t=-3.73，p＜0.05），县城学生数学学科能力表现总体优于乡镇学生。具体来看，县城和乡镇两类地区概念理解、推理能力、运算技能这三维度均存在显著差异（p＜0.05），县城学生在这几方面的表现均好于乡镇学生；而在几何直观维度，虽然县城学生的发展水平与乡镇学生在统计学意义上不存在显著差异（t=4.36，p＞0.05），但是乡镇中学生几何直观方面的得分率（0.38）要高于县城学生（0.34），乡镇初中生几何直观方面表现较好。

2.Y 县的城乡中学生数学学科能力具体差异状况分析

两类地区初中学生在各能力维度上的具体表现及差异状况，具体见图2。总体来看，在水平1 上，县城八年级学生各数学学科能力总体得分率为0.82，乡镇总体得分率为0.81，县城学生表现情况要略好于乡镇。其中在概念理解方面，县城中学生得分率与乡镇中学生得分率均为0.81；在运算技能方面，县城学生在运算技能方面表现略好；在几何直观、推理能力方面，县城中学生仍保持较好的趋势，略高于乡镇学生。在水平2上，县城学生表现情况要好于乡镇。其中在概念理解、运算技能、几何直观方面，县城中学生的得分率均高于乡镇学生；而在推理能力方面，乡镇学生在难度水平2 试题中的推理能力表现要好于县城学生。在水平3上，县城学生表现情况总体要好于乡镇。其中在运算技能、推理能力方面，县城中学生的得分率均高于乡镇学生；而在几何直观方面，乡镇学生在难度水平3 试题中的几何直观方面的表现要明显好于县城学生。

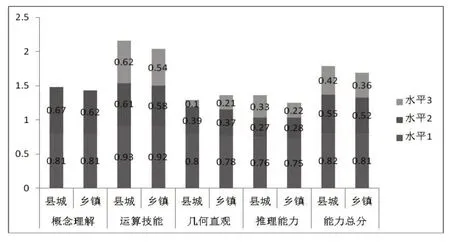
图2 Y县城乡中学生数学学科能力具体差异比较

四、结论与思考

（一）结论

1.县域中学生概念理解水平最高，推理能力水平较低

总体来看，Y 县中学生的数学学科能力总体水平良好。其中，Y县中学生在概念理解维度的得分率最高，表现较好；在运算技能、几何直观维度学生表现次之；学生在推理能力方面的得分率相较其他数学学科能力水平较低。具体来看，Y县中学生在每一数学学科能力维度的不同难度水平上的表现也不均衡。在各能力维度上，Y 县中学生在水平1 上表现最好，在水平3上表现相对较差。除概念理解维度没有考察学生水平3 的试题外，通过比较其他三方面能力发现：在运算技能维度，学生在水平1上表现最佳，其次为水平2与水平3；在几何直观维度，Y 县中学生在水平3 上表现相较水平1、2 较差；在推理能力维度，学生在水平1 上的表现最佳，水平3 次之，水平2 较差。综上所述，Y 县中学生数学学科能力水平呈现不均衡状况。

2.Y 县的城乡中学生数学学科能力发展水平不均衡

总体来看，Y 县的县城和乡镇两类地区中学生的各数学学科能力之间存在显著差异，县城中学生数学学科能力总体水平要比乡镇的总体水平高。其中，在几何直观方面Y 县的乡镇中学生表现好于Y县的县城中学生，其他三方面均为县城比乡镇的中学生表现好。具体来看，Y县的县城和乡镇两类地区中学生在三个水平上的表现出不均衡性，在三个水平上县城中学生数学学科能力表现均好于乡镇中学生。其中，在水平2 上的推理能力方面以及水平3上的几何直观方面，乡镇中学生表现均优于县城学生。其余均为县城中学生表现较好。综上所述，Y 县的县城中学生和乡镇中学生数学学科能力发展水平较不均衡，并出现两极化分布的现象。

（二）思考

影响县域中学生数学学科能力发展的因素涉及诸多方面，如社会、教师和学生自身因素等，综合以上结论与分析本研究大致归结出以下几点思考：

首先，根据以上分析可以发现县域中学生数学学科能力水平发展不均衡，学生概念理解水平最高，推理能力水平较低。其主要原因是我国的数学教育中概念理解占据了基础性地位，是数学思维、理解数学的基础；而数学推理能力则属于学生在数学观念系统下，综合运用数学知识、方法进行判断的思维能力。相对于概念理解，推理能力是一种更为综合的数学思维能力，对学生要求更高。教师也更重视基础性知识与技能，对于学生综合运用数学知识进行思考的培养还有待加强。为能够均衡发展学生的数学学科能力，教师应加强薄弱模块的教学，注重学生数学思维过程，才能够最大程度地使学生的数学学科能力得以均衡发展。如中学阶段，学生已经具备一定的简单推理能力，学生完全能够通过数学推理得到“数与代数”领域的相关结论，教师可以充分利用这一特点，在该领域的教学中适当让学生通过已有知识进行数学推理得到新的结论，加强学生数学推理能力的培养。此外，教师还可以充分利用丰富的教学材料与教具等培养学生的推理能力。如北师版八年级上册的教材中专门设置了一个章节的内容培养学生的数学推理能力，教师可以将该章节内容融入日常的教学中，潜移默化地培养学生数学推理的意识，从而促进学生数学学科能力的全面、均衡发展。

其次，在分析Y 县的县城和乡镇中学生数学学科能力水平状况时，发现城乡学生数学学科能力存在显著差异，县城中学生数学学科能力发展水平总体要高于乡镇中学生数学学科能力水平，仅在个别学科能力的个别水平上呈现出“乡”比“城”好的现象。造成这种城乡差异状况的主要原因是城乡教育资源配置的不均衡。有研究表明，加大农村地区中小学教育经费的投入会带来更大的产出效应，且加大师资培训力度、改善办学条件等措施会更有助于学生成绩的提高。［6］Y 县城乡学校之间的教育资源配置存在很大差异，乡镇学校教育资源相对不足，尤其在人力资源方面，乡镇学校师资力量相对匮乏，有的数学教师则非数学专业出身，且没有经过专业的数学教育培训，并不能很好地理解数学知识间的关系与数学学科能力各方面的内涵，在教学中会制约学生某些数学学科能力的发展。因此，为均衡城乡学生数学学科能力的差异，应该适当加大对乡镇学校的经济投入，加强教师队伍的建设，增加城乡教师培训、集体教研等活动，从而提高学生数学学科能力的发展。除此之外，城乡差异具有双向性，在缩小城乡之间的差距时，也不能忽视乡镇比县城好的现象。在乡镇学校表现优异的方面，应鼓励乡镇学校教师进行深入分析，发掘自身优势，利用优异模块带动薄弱模块学习，分享学生数学学科能力培养经验。