基于环境因素的露天煤矿粉尘质量浓度预测
2021-12-21栾博钰王春丽周永利赵彬宇
霍 文,栾博钰,周 伟,陆 翔,王春丽,周永利,赵彬宇
(1. 神华准格尔能源有限责任公司 信息中心,内蒙古 鄂尔多斯 010300;2. 中国矿业大学 矿业工程学院,江苏 徐州 221116;3. 神华准格尔能源有限责任公司 科学技术研究院,内蒙古 鄂尔多斯 010300)
0 引言
随着环保要求的提高,国内诸多露天煤矿装备了环境监测系统,主要用于监测PM2.5、PM10、TSP等环境指标.风速等是影响粉尘质量浓度的主要环境影响因素[1-2],但是单纯监测无法得到未来某环境因素影响下的粉尘质量浓度,难以准确通过增加洒水量等作业调节方式及时抑制高浓度粉尘.
机器学习算法是人工智能技术的核心技术之一,如神经网络、支持向量机、随机森林等算法,挖掘潜藏在大数据之中的逻辑关系以实现对数据预测、图像识别、自然语言处理等功能.李慧民[3]等提出一种基于随机森林算法的采空区煤自燃预测模型,能够可靠地预测采空区煤自燃温度.邓军[4]等提出一种基于粒子群算法和BP神经网络的冲击危险评估方法,用于评价冲击矿压危险程度. DAS S K[5]等通过神经网络建立了露天矿边坡稳定性预测模型,用于预测边坡稳定性系数.黄婕[6]等基于卷积神经网络-循环神经网络(RNN-CNN)深度学习网络建立了PM2.5浓度预测模型,用以预测粉尘质量浓度.李冬[7]等利用支持向量机算法建立了瓦斯含量预测模型,通过概率神经网络(PNN)反演算法得到了构造煤分布情况.温廷新[8]等基于遗传算法-极限学习机(GA-ELM)算法建立了抛掷爆破预测模型预测抛掷爆破爆堆曲线.吴财芳[9]等采用BP神经网络建立了煤层气井产能预测模型,预测煤层气井产能.刘光伟[10]等将生物激励神经网络运用到基于选线道路费用成本最优化数值计算模型中,提高了运输系统道路选线效果.
同种算法不同背景下的数据集无法使用相同参数建立同等有效的预测模型,必须通过参数调节等方法建立适用于目标数据集的预测模型.本文以哈尔乌素露天煤矿环境监测数据作为研究数据集,利用随机森立算法建立适用于哈尔乌素露天煤矿的粉尘质量浓度预测模型,并分析不同特征变量对粉尘质量浓度的影响,为控制粉尘浓度提供理论基础.
1 研究数据
1.1 数据来源
研究数据来源于神华哈尔乌素露天煤矿旧观礼台粉尘监测系统,该监测设备每间隔5 min同步监测一次环境数据,包含空气温度、空气相对湿度、风力、风速、风向、PM2.5、PM10、TSP等.推测噪声一定程度上代表露天矿作业设备的出动情况,因此将噪声作为预测模型特征变量之一,以便可以提高预测准确性.
1.2 数据分析
本研究选取2018年11月8日至2018年11月30日的数据作为研究数据,总计6 336组.图1为PM2.5、PM10、TSP随时间变化曲线,3个曲线变化基本一致,具有较强相关性,数据具有一定浮动,但对整体变化趋势影响较小.
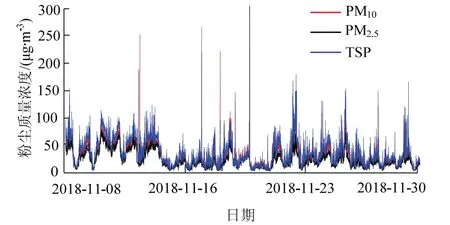
图1 粉尘质量浓度变化 Fig.1 variation of dust mass concentration
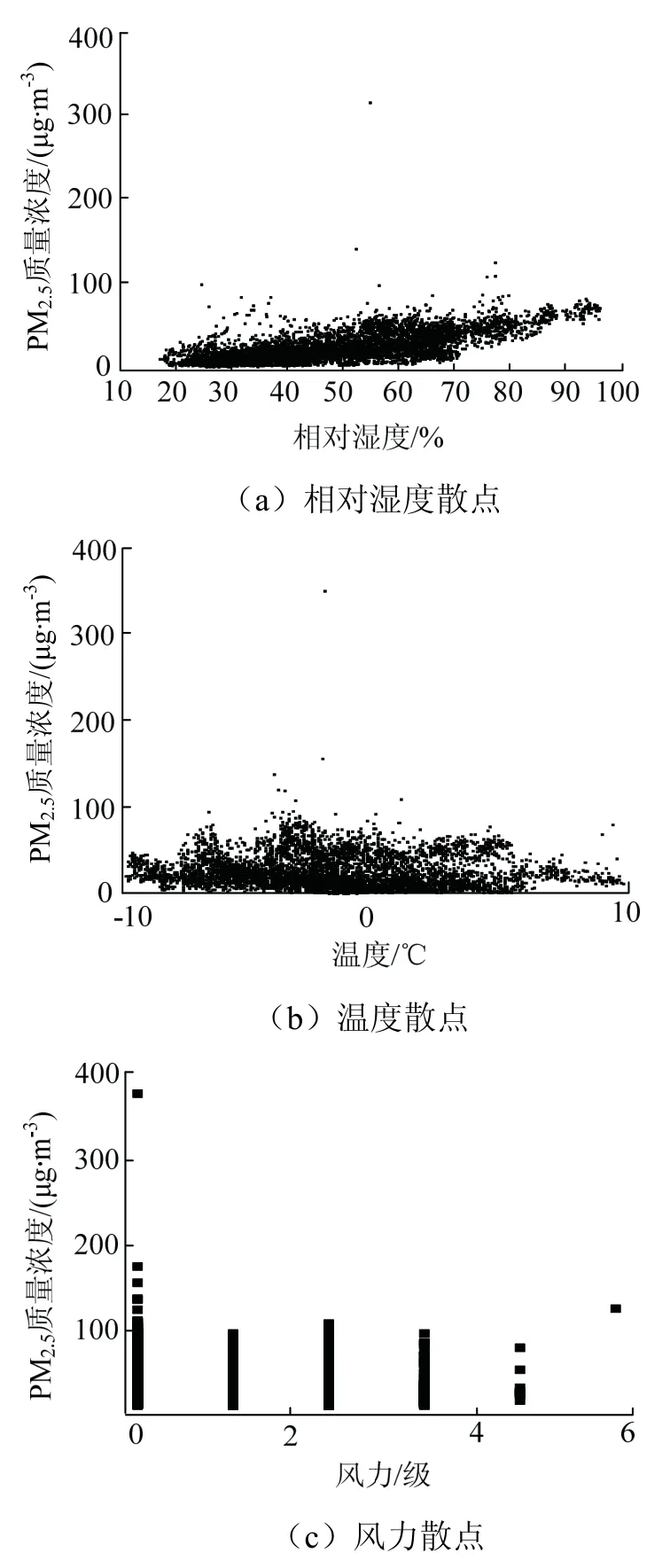
为观察数据之间的相关性,将PM2.5与其他特征变量绘制成图2和图3,不同特征变量与粉尘质量浓度之间散点较为聚集,数据中离散数据相对较少,表现出良好的相关性,可以用于机器学习算法.
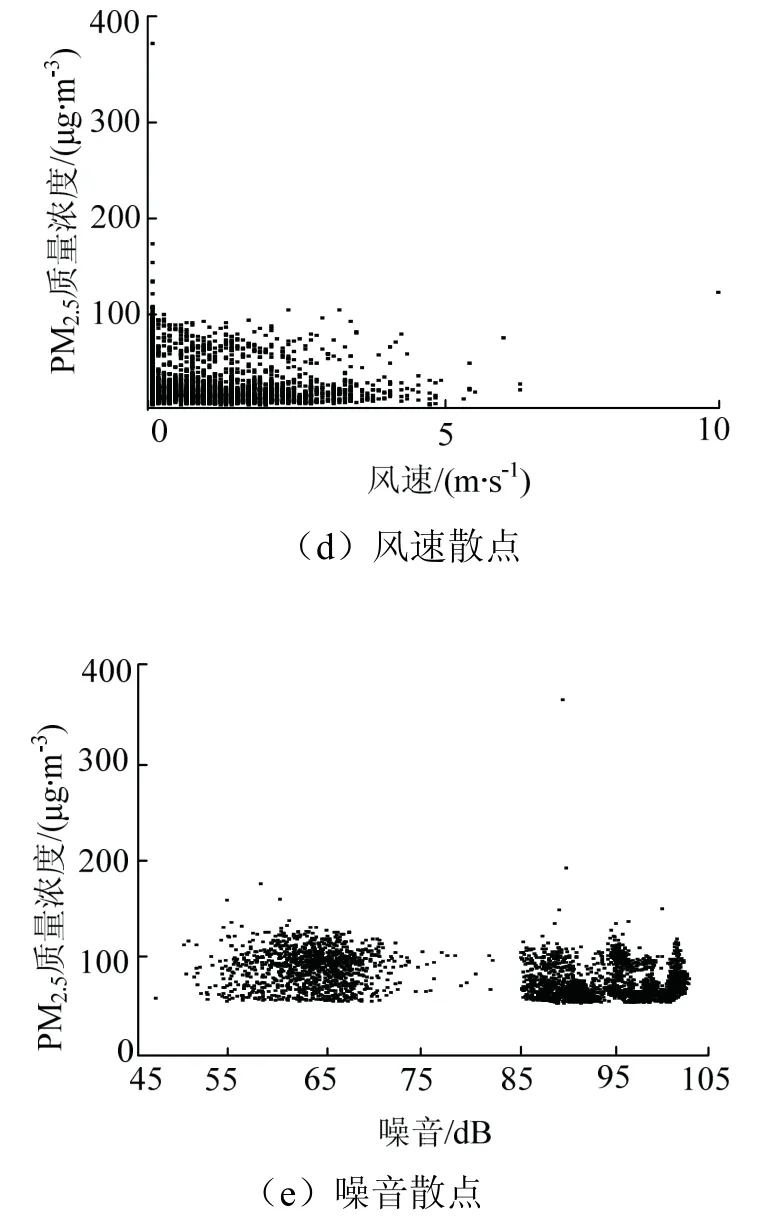
图2 特征变量散点 Fig.2 scatter plot of characteristic variable
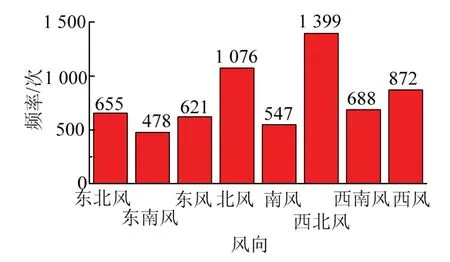
图3 风向统计 Fig.3 wind statistics
2 研究方法
2.1 随机森林算法
随机森林算法是决策树算法的一种集成学习算法,属于非参数学习算法,具有良好的噪声容忍度.决策树是一种树形结构的决策算法,每一个叶节点代表一种决策条件,每一条分支代表一种决策结果.随机森林算法能够有效地在n个随机子集上寻找最优划分特征的决策树,通过加权投票方式克服决策树对个别数据敏感度高与过拟合部分数据集的缺点.随机森林算法示意见图4.
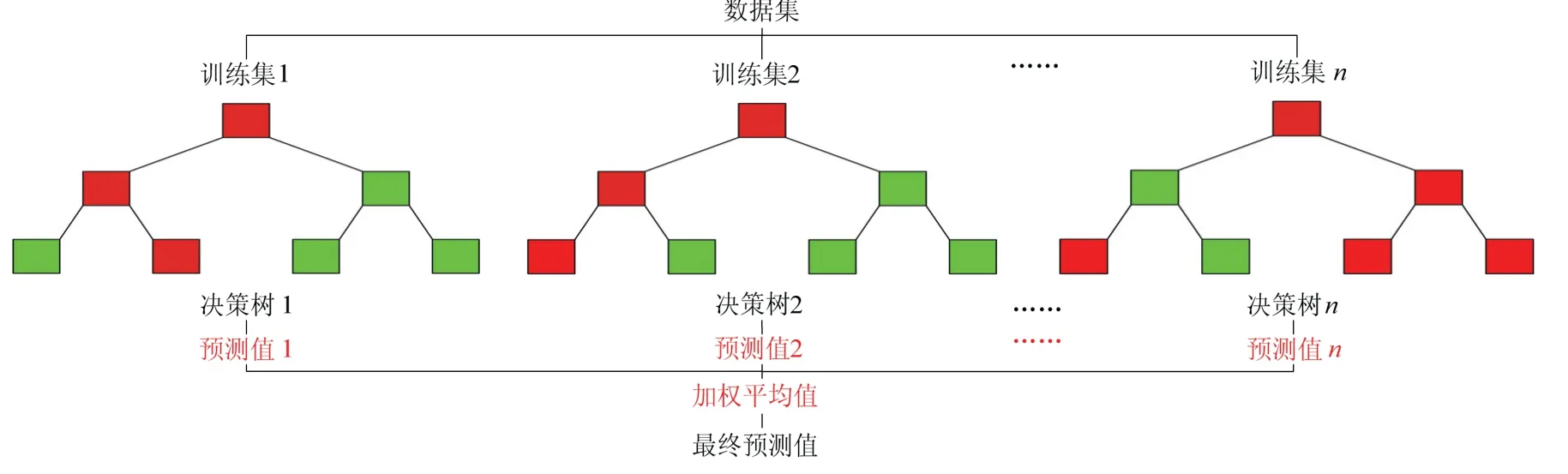
图4 随机森林算法示意 Fig.4 schematic of random forest algorithm
2.2 数据预处理
从图2可知粉尘质量浓度数据噪点较大,整体变化趋势明显,但局部数据浮动程度高,少数数据出现较大突变,理想中的粉尘质量浓度变化应当是连续的曲线.因此为提高预测效果,对粉尘质量浓度数据进行降噪处理.
除两端点以外的点与邻近左右两点的平均值做均值化,即
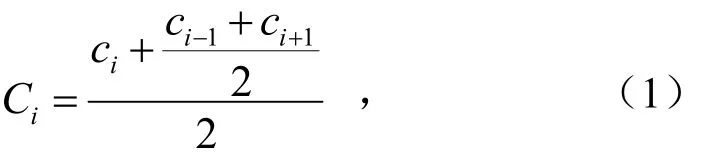
式中,i>1;Ci为第i个点降噪后粉尘质量浓度,μg/m3;ci为第i个点降噪前粉尘质量浓度,μg/m3.
为检验模型预测准确度,将2018年11月8日至2018年11月24日之间的4 608组数据作为训练集,2018年11月24日至2018年11月30日之间1 728组数据作为测试集.
对训练集进行降噪处理过程中,由于原始数据波动性较强,单次降噪后效果不明显,需要多次迭代降噪.以100为单位对原始数据进行迭代测试,以预测效果为评判标准,当迭代次数为2 000时降噪效果最佳.降噪后效果见图5,降噪后曲线可以很好地贴合原有数据的变化趋势,达到了降噪的目的.
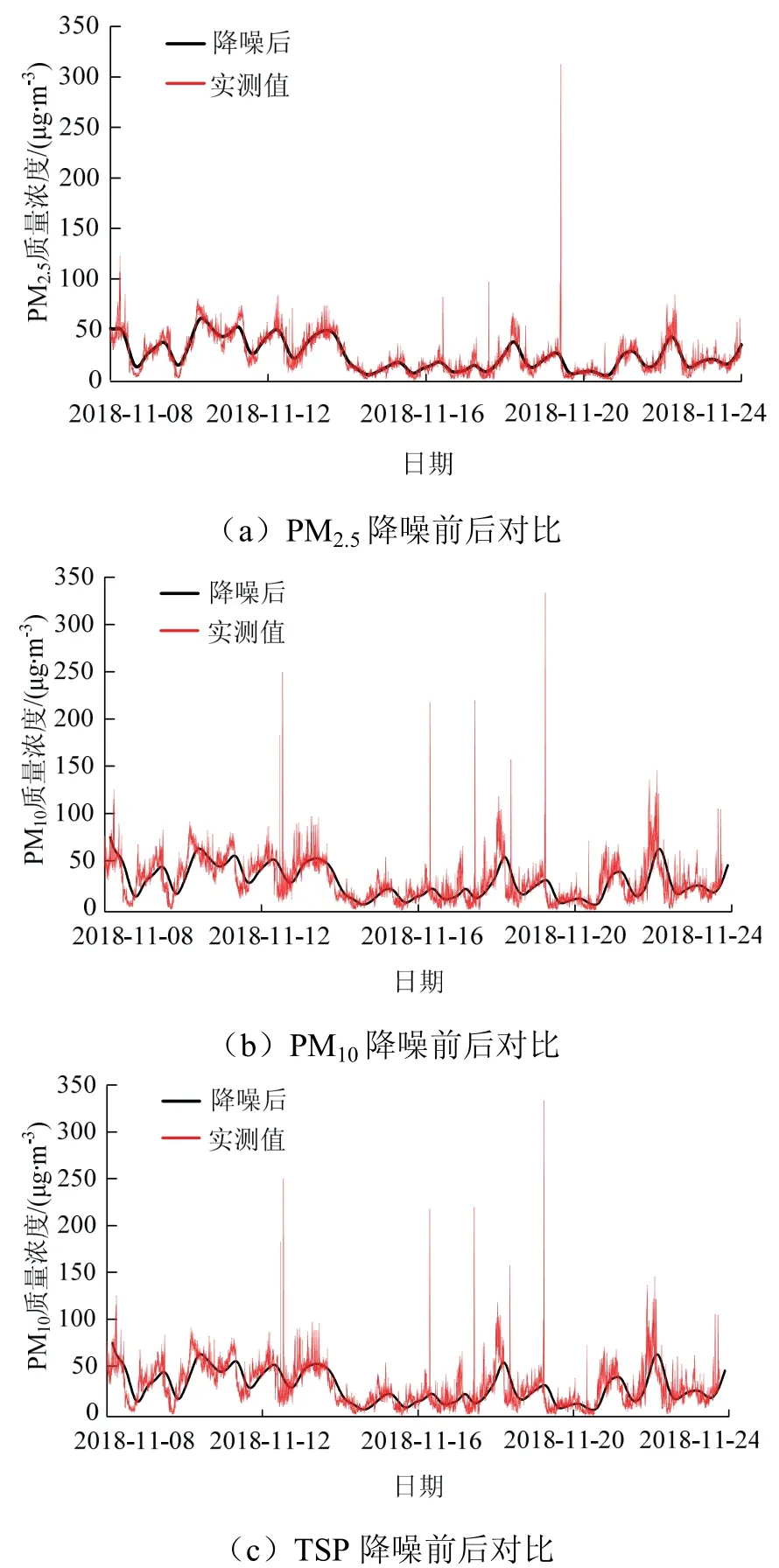
图5 降噪数据对比 Fig.5 data comparison of noise reduction
2.3 模型建立
采用网格搜索的方法对随机森林模型进行参数调整,对决策树最大深度、节点最少样本数、节点可分最小样本数均在0~20进行搜索,得出最优超参数,结果见表1.

表1 最优超参数 Tab.1 optimal hyperparameters
3 结果与讨论
3.1 预测模型效果评价
将测试集代入基于训练集建立的随机森林预测模型进行粉尘质量浓度预测.预测模型评价指标的均方根误差为
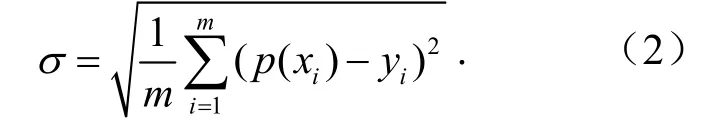
式中,σ为均方根误差;m为数据数量;p(xi)为预测值,μg/m3;yi为实测值,μg/m3.
表2为预测结果的RMSE.从表2结果来看,降噪后不同粉尘类型的预测准确率均有所提高.
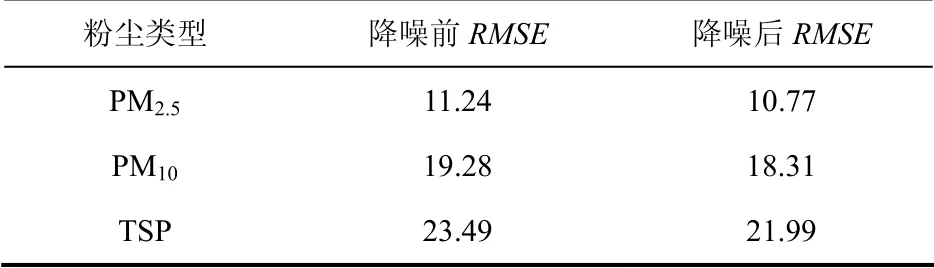
表2 预测结果 Tab.2 forecast results
3.2 特征变量重要性分析
随机森林算法在建立不同决策树时采取随机且有放回的抽取方式,因此每一颗决策树不会用到全部的训练数据,未被使用的数据被称为袋外数据.特征变量重要性计算原理见式(3).
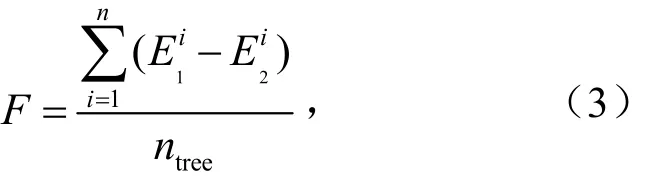
式中,F为特征变量重要性;E1i为第i棵决策树袋外数据预测误差,μg/m3;E2i为第i棵决策树袋外数据噪声化后预测误差,μg/m3;ntree为决策树数量.
图6为粉尘质量浓度预测结果,降噪后的曲线在降噪前预测结果偏离较大的位置得到了改善,主要体现在真实值局部数据突变的噪点,部分预测数据曲线更为稳定,浮动较小,改善因局部数据噪点而导致的模型失真.降噪后除2018年11月24日以外的天数预测效果均有提高,2018年11月24日预测效果反而降低,主要原因在于随机森林算法对数据的敏感性较高.
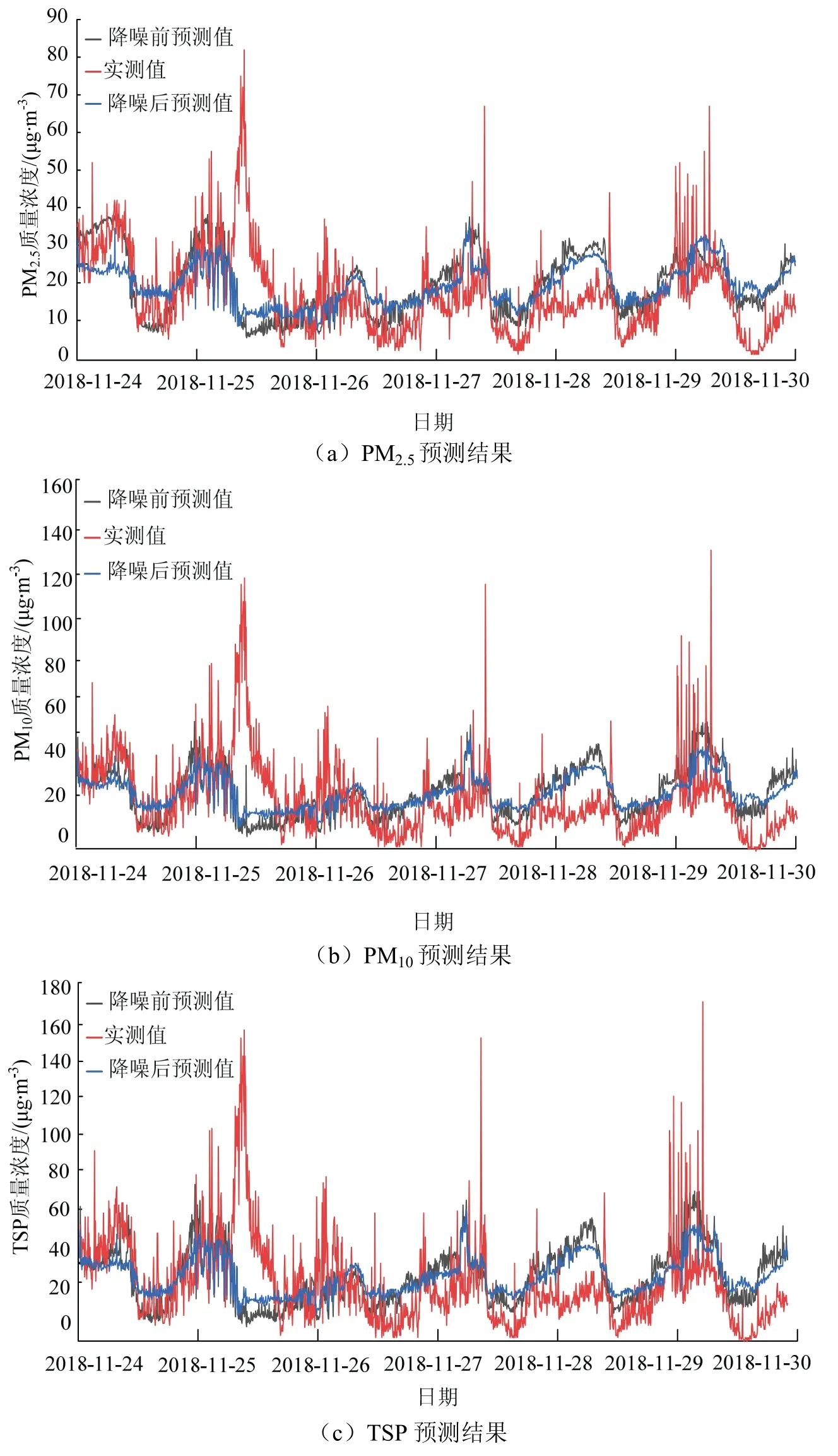
图6 3种粉尘颗粒质量浓度预测结果 Fig.6 prediction results of mass concentration of three dust particles
该计算原理是基于数据对预测准确率的敏感性,若某一特征变量数据在加入噪声后数据预测准确率下降幅度较大,则认为该特征变量重要性较强.
本研究特征变量重要性计算结果见图7.这3种粉尘颗粒的影响因素整体趋势相同,相对湿度最重要,且重要性远高于其他特征变量.风向由于包括8种不同风向,因此风向重要性最低.
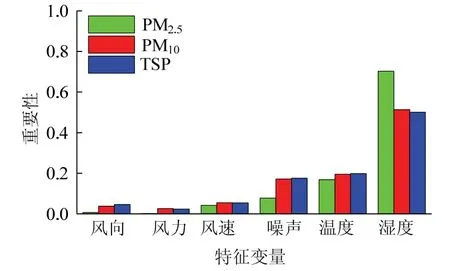
图7 特征重要性 Fig.7 feature importance
比较3种粉尘颗粒特征重要性,PM10与TSP结果相近,比较之下相对湿度对PM2.5重要性相对更高,噪声对PM2.5重要性相对较低.主要原因分析如下.
(1)相对湿度即空气中的水含量,水雾可以有效的捕捉10~20 μm的粉尘颗粒,但1~10 μm的粉尘颗粒水雾难以捕捉[11],因此PM2.5对相对湿度敏感性高于PM10和TSP[1].
(2)噪音在一定程度上可以代表开采强度,PM2.5相较于PM10与TSP更容易逸散出矿坑[12],因此噪音对旧观礼台(矿坑边缘)监测得到的PM10与TSP影响更大.
4 结论
基于环境数据通过随机森林算法对哈尔乌素露天煤矿监测点粉尘质量浓度进行预测研究,主要得出以下结论:
(1)哈尔乌素露天煤矿旧观礼台粉尘监测点环境数据,随机森林方法可以对粉尘质量浓度做出良好预测.
(2)对粉尘质量浓度数据降噪处理可以提高整体模型预测准确性.
(3)环境影响因素中的相对湿度是对预测效果影响最大的特征变量,其次是温度、噪声,风速、风力、风向影响较小.
