因素空间理论下多目标因果分析的降维算法
2021-12-21曾繁慧蒲凌杰
孙 慧,曾繁慧,蒲凌杰
(1.辽宁工程技术大学 理学院,辽宁 阜新 123000;2.辽宁工程技术大学 智能工程与数学研究院,辽宁 阜新 123000)
0 引言
1982年汪培庄提出因素空间理论,为概念、判断、推理等的数学描述提供了理论框架,并于1994年与李洪兴合写著作《知识表示的数学理论》[1].因素空间是以因素为轴的坐标架,主要有两大分支,其一是背景基理论.背景基可以生成背景关系,它是背景关系的无信息损失的压缩,对因素库[2]的实际应用具有重要的意义,背景关系是因素空间的形骸,塑造这个形骸的工具就是背景基,文献[3]提出了背景基的概念;文献[4]针对随机性和模糊性的特点,提出了因素空间的背景分布和模糊背景关系;文献[5]把由汪培庄提出的钝角删除法上升为精确算法.
因素空间另一个主要分支是因果分析法,因果分析法能在一张因素分析表中自动找出表中所含的因果关系,并画出因果图.文献[6]按照因素空间的理论框架,在离散情形下定义了条件因素对结果的决定度及决定域,依次从决定域上提取出相应的推理知识,得到一种新算法为因果分析法.文献[7]为进一步提高因素空间中因果分析法的运行速度和对样本信息的利用,对文献[6]给出的因素分析算法进行了改进.文献[8]为进一步扩大因素空间中的因果分析法的应用领域,提出了多标准因果分析算法.因果分析法可以广泛地应用到各种领域[9-11],特别是数据挖掘,与数据挖掘决策树方法相比,因果分析法使用起来更简洁、贴切.然而当目标因素数量较大,利用多目标因果分析法计算的过程会十分繁杂,因此,本文提出一种降低目标维度的算法.
首先给出多目标因素条件下降维映射和钻入决定度降维的定义,然后将未被选定的目标因素进行合取,分析合取因素对选定目标因素的钻入决定度是否为1,进行目标因素的约简,得到了目标因素的降维算法,接着在目标因素的降维算法的基础上,研究了目标因素之间的关联性,给出了关联指标定义,又结合多目标因果分析法,得到了多目标因果分析降维算法,并作出实例分析.
1 预备知识
首先介绍因素空间的相关基本理论[3].
定义1因素是映射,把对象映射到其属性上.映射是分析,因素是分析的维度.因素是映射,其中D为论域,即讨论对象.I(f)为因素的相域.a1,…,ak是其中的相.
定义2论域D上的一个集合族 为D上的一个因素空间.

通常,只要两个事物不同,就至少存在一个因素,使它们的因素状态完全不同.
定义3给定D上的定性因素空间,对任意a=(a1,a,…,an)∈I,记其在D上的原相为[a]=F-1(a)={d∈D|F(d)=a},[a]可能是空集∅,若[a]=∅,则称a是一个虚组态,否则a是一个实性状颗粒.全体实性状的集合记为
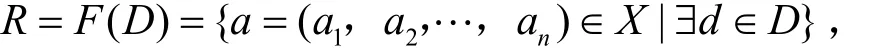
式中,R为因素f1,…,fn之间的背景关系.
定义4如果背景关系

则称因素f与g独立.
定理1背景关系决定一切恒真推理句:若,则E(x) →E′(y)必是恒真句.恒真句也叫因果规则律,从因素表提取,因果律也叫规则提取.
定义5给定因素空间
定义6设记

如果[s]⊆,[t] 则称[s]是因素f的一个决定类.因素f的所有决定类的并集称为对结果的决定域.因素f的决定域所占行数h与表的行数(即全体对象个数)m之比称为其对结果的钻入决定度,记作
因果分析法是因素空间理论下的一种提取规则的算法,是一种能体现人脑认知中归纳和推理的基本方法,因果分析法可以应用于离散型数据的分类和归纳.
因果分析法的整个流程可以概括成3步:①选取决定度最高的因素进行划分;②将所有决定类选取出来,并转化为推理句;③将选取的决定类所对应的地址从因素表中删除,重复上述步骤,直到表被删空.
2 多目标因果分析降维算法
2.1 多目标因果分析法
因果分析法是基于树结构来进行规则提取的,也可以称为因果树算法,这也是人类在分析问题时的一种很自然的处理机制.例如,某超市要对“个人的购买力”进行分析时,通常会进行一系列的判断或“子分析”:首先看“这个人的还贷能力”,如果是“可”,则再看看“他的职业”,如果是“商”,再判断“他的年龄是多少”,得出结果:这个人会“购买”.分析过程见图1.

图1 购买问题的一棵因果树 Fig.1 a causal tree of purchase problem
因果树是一种有效的分类和归纳方法,它具有很强的概括性,并能将形似信息与效用信息关联起来,提升为全面的语义信息.
因果树算法是多个条件因素对应一个目标因素,在条件因素互相关联的条件下,得到条件因素对目标因素的树状结构,但是这种算法具有局限性,在实际应用中常常需要考虑的是多个条件因素对多个目标因素,所以就有了多目标因果分析方法,多目标因果分析方法是在因果树算法的基础上,利用钻入决定度所得到的.多目标因果分析方法避免了因果树只解决一个目标因素的局限性问题.
定义7如果因果规则后件中不完整,即因果规则只能得到条件因素对应不完整的结果,则称此因果规则是残缺的.
定义8因素fi对所有目标因素的总决定度ci,,其中,hir为第i个条件因素对第r个目标因素的决定域所占行数,um为当前划分类所占的总行数.
多目标因果分析法步骤如下.
步骤1先将所有连续型的条件因素和目标因素通过等步长进行离散化处理.
步骤2计算每个条件因素对所有的目标因素的总决定度ci,找出总决定度最大的条件因素,用此条件因素的相域将论域D进行划分;若出现决定类,就写出相应的因果规则,若是因果规则是不完整的,则继续上述步骤,直到因果规则是完整的或者因素不能再分为止.
步骤3将所有因果规则进行归纳,得到一棵因果树.
2.2 目标因素的降维算法
因果分析是多个条件因素对单一目标所进行的规则提取,多目标因果分析是多条件因素对多个目标所进行的规则提取.目前算法是:对每个条件因素求出它对各个目标因素的钻入决定度而得到一个决定度向量.对这个向量定义某种范数(如本文前面所定义的总决定度),根据这个范数来选取因素对D中对象分类,将决定类转化为推理句,如此巡回,直到全部论域都转化为推理句.
目标因素之间往往不是独立的.如果它们不独立,则可先在目标因素之间进行因果分析,如果目标甲和乙决定目标丙,则目标丙就可以先拿开,仅对甲乙这两个目标来进行因果分析,得到一组推理规则以后,再把目标丙的相值按照目标因素之间的关系填补回去.本文定义了降维映射和钻入决定度降维,将未被选定的目标因素进行合取,分析合取因素对选定的目标因素的钻入决定度是否为1,进行目标因素的约简,此算法称为目标因素的降维算法.
(1)算法原理
定义9(降维映射) 论域D中有m个对象,r个目标因素,目标因素指标集J:={1,…,r},目标函数集H0:={g1∧…∧gr},目标函数相I(H0),当选出第j个目标因素gj,j∈J,其余目标因素的合取因素Hj:= ∧{gi|i∈J,i≠j},如果函数f(I(Hj))能够映射到函数f(I(gj)),即I(Hj)对I(gj)只有一对一和多对一关系,不存在一对多关系,则可以将gj进行降维约简.
其中,

定义10(钻入决定度降维) 当I(Hj)对I(gj)只有一对一和多对一关系,不存在一对多关系时,那么钻入决定度Zj=1,此时可以将gj进行目标降维.
算法核心思想为钻入决定度为1的时候,条件因素的取相完全决定了目标因素的取相,是目标降维的依据.
算法降维原理如下.
① 给定多目标因果分析的数据表,只看目标因素列,记H0:={g1∧…∧gr},将H0中任何一个拿出来当做目标因素,考察其余因素的合取因素对其的决定度是否为1.

求因素Hj对因素gj的决定度Zj.如果所有Zj<1,则放弃目标降维,用常规的多后件因果分析处理,否则,任意取定一个具有决定度Zj=1的因素Hj,记下相应的函数关系式,去掉目标因素gj;
③ 对剩下的因素再重复这一过程,把Hj中任何一个因素拿出来当做目标因素,考察其余因素的合取因素对它的决定度是否等于1,若有,则继续删除目标,直到不可再删为止.
这样就实现了目标降维的目的.按降维以后的目标常用算法求多目标因果分析,再按函数关系把被删的目标值一一补齐,就得到原多目标因果分析算法所要得到的结果,但计算量却减少很多.
(2)算法步骤
多目标因果分析降维算法的步骤如下.
将所有连续型的条件因素和目标因素通过等步长进行离散化处理.
设置目标因素指标集J:={1,…,r}.
步骤1对j∈J,记,计算合取因素Hj对gj决定度Zj(合因素的决定度怎样计算,见下例);若Zj,则在J中更换下一个指标,若J中别无其它指标,则转向步骤2;若Zj=1,则写出函数句(函数句的写法,见下例);将足码j从J中删掉;若|J|=1,则转向步骤2;否则重新执行步骤1.
步骤2将J中所剩下指标所对应的因素作后件,整理并归纳得到的目标取值的函数关系句.
2.3 多目标因果分析降维算法
根据上文提出的目标因素的降维算法,结合多目标因果分析法,研究了目标因素之间的关联性,提出了多目标因果分析降维算法.目标因素之间的关联性越强,算法的效果就越好,多目标因果分析降维算法可以反映目标因素之间的内在联系.
定义11(目标因素之间的关联性)目标因素g1,g2,…,gr的背景关系R与目标因素相域I(g):=I(g1) ×I(g2) × … ×I(gr)(去掉虚组态)是否相等,如果R=I(g),则称g1,g2,…,gr是相对独立的.如果R≠I(g),则称目标因素g1,g2,…,gr之间有关联,关联指标σ:= |R|-|I(g)|,σ越大,目标因素之间的关联性越强,其中|R|,|I(g)|分别为R和 ()Ig的种类个数.
多目标因果分析降维算法步骤如下.
步骤1先将所有连续型的条件因素和目标因素进行离散化处理,例如通过等步长作离散化.
步骤2对目标因素进行关联性计算.
步骤3对j∈J,记,计算合取因素Hj对jg的决定度Zj;若Zj<1,则在J中更换下一个指标,若J中别无其它指标,则转向步骤4;若Zj=1,则写出目标取值的函数关系句;将足码j从J中删掉;若,则转向步骤4;否则重新执行步骤3.
步骤4将J中所剩下指标所对应的因素作后件,整理并归纳得到的目标取值的函数关系句.
步骤5计算每个条件因素对所有的目标因素(目标因素是步骤4中的降维后的后件)的总决定度ci,找出总决定度最大的条件因素,用此条件因素的相域将论域D进行划分;若出现决定类,则写出相应的因果规则,若是因果规则是不完整的,则继续上述步骤,直到因果规则是完整的或者因素不能再分为止.
步骤6将所有因果规则进行归纳,按照步骤4中的函数关系句补齐因果规则,得到一棵因果树.
3 实例验证
用一个实例验证本文给出的多目标因果分析降维算法.对于超市用户的消费情况进行因果规则提取,条件因素有年龄、收入、职业、还贷能力4个,目标因素有消费金额、消费状况、消费间隔3个.超市用户的因素分析数据见表1.

表1 超市用户的因素分析 Tab.1 factor analysis of supermarket users
表1有4个条件因素.

表1有3个目标因素分别具有相域.

(1)多目标因果分析降维算法
步骤1首先确定目标因素之间的关联性,目标因素相域I(g)={(111),(112),(212),(221),(311),(322)}(去掉虚拟态)共有6个组态,目标因素背景关系

共有12个相组合,所以|R|,|I(g)|分别为12和6,σ=|R|- |I(g)|= 6,表明这3个目标因素之间有强关联性.
多目标因果分析降维算法:设置目标因素指标集J:= {1,2,3}.
步骤2取j= 1,记H1=g2∧g3,计算合取因素H1对g1的决定度Z1,合取因素g2∧g3的相值是表中右2与右1两列相值的组合.例如用户1的合取相值是向量(2,2),用户2的合取相值是向量(1,2).全体用户的相应相值共有(2,2),(1,2),(2,1)和(1,1)4类.要使11Z=,当且仅当这4类都能钻入由1g所分出的类,现在(2,2)类所对应的1g值都是3,(1,2)类所对应的1g值是2,(2,1)类所对应的1g值是2,都钻入了1g的类,但是,(1,1)类的1g值为1或者3,不能钻入1g的类,因而11Z<.程序要求在J中更换下一个指标2,重新执行步骤1.
取j=2,记H2=g1∧g3,计算合取因素H2对g2的决定度Z2,这里合取因素g2∧g3的相值是表中右3与右1两列相值的组合.全体用户的相值共有(3,2),(3,1),(2,2),(2,1),(1,1)和(1,2)共6类.(2,2)类、(1,1)类,(3,1)类和(1,2)类所对应的g2值都是1,(2,1)类和(3,2)类所对应的g2值都是2,都钻入了g2的类,因而Z2= 1.于是,目标g2可以被视为g2的函数,写成目标取值的函数关系句如下.

记下这组推理句以后,把2从J中删除,变为J= {1 ,3};重新执行步骤1.
取j=1,有H1=g3,此时,需要判断H1=g3对g1的决定度是否为1,因g3= 2时g1可以取值为1,也可以取值为2或3,故知决定度不可能等于1;按照程序,从中取出另一个指标,取j= 3,有H3=g1,需要判断H3=g1对g3的决定度是否为1,因g1=3时g3有时取2有时取1,故知决定度不可能等于1;按照程序,转向步骤3.
步骤3降维后的后件是J中现有的指标所对应的目标因素g1和g3,前件是f1,f2,f3,f4,目标取值的函数关系句是(I)~(VI).
步骤4(1)先判断f1对g1是否存在决定类.当f1以“老”为相,看g1的相是否相同,表1中,用户1和用户5的I(f1)为“老”,他们的I(g1)分别为3和2,因为不同,所以“老”不是f1的一个决定类;用户2和用户4的I(f1)为“中”,他们的I(g1)分别为2和1,所以“中”也不是f1的一个决定类;用户3、用户7、用户8、用户10和用户13的I(f1)为“青”,且I(g1)均为3,所以f1对g1存在决定类,决定类中的对象个数为5.同理可知,f1对g3不存在决定类,所以f1一列记为(5,0)=5.类似地,可以判断f2,f3,f4对g1和g3是否存在决定类,在此不再细算,直接给出结果,f2一列记为(4,0)=4;f3一列记为(4,0)=4;f4一列记为(6,9)=15,由于f4取值最大,所以选择f4作为下一步划分.
(2)对f4进行划分,划分结果如下.

(3)重复第一步,分别计算I(f4)为“可”和I(f4)为“好”的用户.
先计算I(f4)为“可”的那三行的总决定度,直接给出结果,f1一列记为(3,3)=6,总决定度为2;f2一列记为(1,3)=4,总决定度为4/3;f3一列记为(1,3)=4,总决定度为4/3;f4一列记为(0,3)=3,总决定度为1.
f1的总决定度最大,在I(f4)为“可”的前提下,继续按f1进行划分,划分结果如下.

继续计算I(f4)为“好”的那六行的总决定度,直接给出结果,在I(f4)为“好”的前提下,划分结果如下.

步骤5将所有因果规则进行归纳,并画出最后的因果树.
10条因果规则:差→32;可青→31;可中→11;可老→21;好青→31;好中高→11;好中平师→22;好中平商→12;好老师→12;好老商→11.
上述得到的因果规则只包含两个目标因素,要想得到被约简的目标的取值情况,参照目标取值的函数关系句(I-VI)来补齐.例如,把关系(I)(g1=3且g3=2)→g2=2;连接在因果规则(1)之后,便有:f4差→g1为3,g3为2→g2=2,写成补齐式.
(1) I(f4) =差→ I(g1) =3,I(g2) =2,I(g3) =2.(根据(I))
类似地有
(2) I(f4)=可,I(f1)=青→I(g1)=3,I(g2)=1,I(g3)=1.(根据(II))
(3) I(f4)=可,I(f1)=中→ I(g1)=1,I(g2)=1,I(g3)=1.(根据(V))
(4)I(f4)=可,I(f1)=老→I(g1)=2,I(g2)=2,I(g3)=1.(根据(IV))
(5)I(f4)=好,I(f1)=高→I(g1)=1,I(g2)=1,I(g3)=1.(根据(V))
多目标因果树,见图2.

图2 多目标因果树 Fig.2 multiple target causality tree
(2)算法对比
利用常规的多目标因果分析法,进行超市用户消费情况的因果规则提取,具体步骤不再描述,得到的结果与多目标因果分析法相同,接下来对比常规多目标因果分析法和带有目标降维的多目标因果分析法的计算时间和计算次数,见表2.
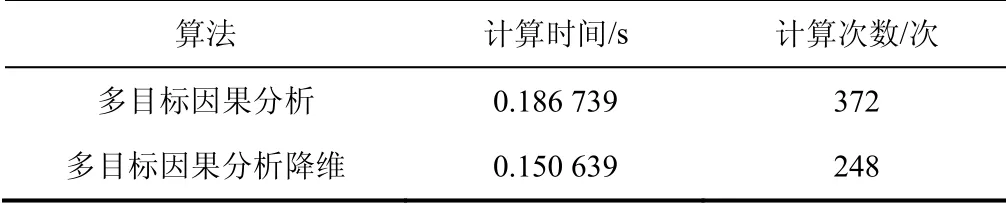
表2 两种算法的计算对比 Tab.2 calculation comparison of two algorithms
从表2中可以看出,多目标因果分析降维算法的计算时间和计算次数均小于多目标因果分析,且两种算法的计算结果也相同,表明多目标因果分析降维算法的计算效率更好,有效地降低了计算的繁杂性.
4 结论
(1)定义了降维映射和钻入决定度降维,将未被选定的目标因素进行合取,做到了目标降维,得到了目标因素的降维算法.
(2)在目标因素降维算法的基础上,定义总决定度,研究目标因素之间的关联性,并给出了关联指标的定义,结合多目标因果分析法,提出多目标因果分析降维算法.
(3)利用某超市数据,进行实例分析,证明多目标因果分析降维算法具有实用性和有效性,并为多目标优化带来新方法.
