合作博弈的连续蚁群算法求解

李壮阔，常凯旋

桂林电子科技大学 商学院，广西 桂林541004

1944年，von Neumann和Morgenstern的专著Theory of games and economic behavior的问世，标志着博弈论的诞生。在该书中，作者用大量篇幅讨论了合作博弈的相关理论，同时考虑了联盟的内部稳定性和外部稳定性，从占优的角度提出了稳定集，这为合作博弈的发展奠定了理论基础[1]。此后，许多学者从不同方向探讨了合作博弈的解概念。合作博弈求解的核心思想是合作均衡，经典合作博弈的解概念可以分为两类：以核为代表的优超法和以Shapley值为代表的赋值法[2]。占优法以“占优”和“异议”为主要准则，体现了稳定性和联盟信息。Gillies考虑局中人的个体理性和联盟的有效性，从占优角度出发，提出核的概念来研究稳定集[3]。Aumann和Maschler将分配结果的形成过程视作局中人的谈判过程，提出了谈判解，体现了分配方案的合理性[4]。Davis和Maschler通过引入了内核的概念来研究谈判解，主要分析了不同局中人对分配方案异议大小的度量的相关问题[5]。Schmeidler提出了核仁的概念，利用超出值来度量局中人对分配方案的不满意程度，从而找出联盟对分配方案集中不满意程度最低的分配方案[6]。赋值法构造一种考虑冲突各方要求的折中的合理结果，通过公理化方法描述解的性质，进而得到唯一的分配方案。Shapley从分配方式的合理性与公平性出发，通过不同局中人对联盟的边际贡献来计算局中人的分配，提出了Shapley值[7]。Myerson提出并研究了具有图限制结构的合作博弈，在Shapley值基础上给出了图限制结构合作博弈的解——Myerson值[8]。基于Myerson的工作，Herings利用图限制博弈和有向树定义了平均树解（A-T解）[9]。Banzhaf考虑联盟中各局中人的权力不同，将局中人的权力大小看作获胜联盟中的关键加入者的个数，使用权力指数比来刻画Banzhaf权力指数[10]。

经典的合作博弈解概念中的假设与现实博弈环境相比过于简单，并且没有考虑到现实中联盟的形成方式。英国著名经济学者布劳格认为：博弈论的全部力量都用于满足经济学家对形式主义模型的沉溺，却不关心模型的现实性如何[11]。合作博弈的求解目标是要找到一个能够形成与维系联盟的分配方案。现实中，联盟分配方案的达成通常是局中人互相影响，不断调整、妥协和趋同的互动过程。如何描述局中人为了合作而竞争，同时又在谈判中趋同是建立合作博弈求解模型的难点。近年来，有学者尝试将复杂的多目标优化问题模型与合作博弈结合在一起。叶文海等提出Isight的博弈多目标优化设计方法，通过合作博弈模型解决多目标系统的求解问题，建立了两者之间的联系，并用遗传算法进行求解[12]。刘雨潇等针对云任务调度优化问题，提出一种基于纳什议价解的多目标合作博弈调度算法[13]。潘颖慧等研究了不确定性多智能体在交互环境下如何优化本身决策，并总结归纳了模型的具体表达方式和求解方法，克服了传统的博弈论求解多智能体决策的局限性[14]。侯德飞等将合作博弈理论应用于部队弹药调度策略问题之中，分别建立合作、竞争合作竞争博弈框架，并用遗传算法对模型进行求解[15]。Xu等将执行器的控制精度优化问题看作一种多目标优化问题，结合合作博弈理论提出了一种分布式模型预测方法[16]。丁阳等针对配电网重构问题，将目标函数作为合作博弈的局中人，通过萤火虫算法计算最终的重构方案[17]。

现实中联盟最终分配方案的达成通常是局中人基于个体理性与判断进行多轮谈判，互相影响、相互妥协、最终趋同的结果。对此，本文将合作博弈的求解过程视作局中人个体博弈和群体趋同的多目标优化问题。考虑到谈判过程中局中人的个体调整和群体趋同行为，引入分配方案、理性因子与控制因子等现实影响因素，构建考虑互动行为的合作博弈模型。在此过程中，对传统连续优化蚁群算法进行改进，提出合作博弈的连续蚁群优化算法对合作博弈模型进行求解。

1 考虑互动行为的合作博弈模型

传统的合作博弈模型是基于团队合作的求解，是集中控制下的资源配置。这种方法存在一个问题，集中配置很容易引发不满，影响局中人间的合作关系。从多个局中人竞争的角度研究联盟分配问题是新的思路，但也需满足合作的要求。相比于传统的求解方法，建模的难点在于如何分析局中人竞争行为与达成共同接受的分配方案两者的协调关系。

联盟中的利益分配过程实际上是一种谈判协商过程，联盟成员会在分配利益时进行谈判博弈。博弈的基本要素有局中人、局中人的分配方案、信息和行动等。在谈判开始前，局中人会根据信息及偏好提出预分配方案。受局中人个体理性，个体偏好和成员关系等因素影响，不同局中人对最优策略的评判标准往往各不相同。因此，在求解过程中需要一个确定的适应度函数作为分配方案的统一评价标准。在每轮谈判过程中，使用谈判档案作为局中人的间接通讯机制，谈判档案可以提供信息流通的渠道进而实现局中人在谈判中的互动行为。局中人通过对谈判档案中的信息进行收集和处理，得到个体最优信息和群体最优信息，依据自身策略、理性、学习情况调整自己的分配方案。局中人对这两种信息的重视程度分别体现了局中人的两种博弈态度。第一种为竞争，局中人追求更高的个人收益，会更看重个体最优信息；第二种为合作，局中人更希望达成合作，会更看重群体最优信息。现实中，局中人对两种信息的重视程度会随局势不断变化，通常表现为前期更看重个体最优信息，后期更看重群体最优信息。最终，通过多轮谈判实现分配方案的趋同。

n人合作博弈记作(N,v)，参与博弈的人称为局中人，所有局中人构成了局中人集N={1,2,…,n},N的任意一个非空子集S为一个联盟，由全体局中人组成的联盟称为大联盟N。大联盟给局中人j分配的收益记为x({j}),x({j})表示局中人j不加入任何联盟时获得的最大收益，v(S)表示联盟S独立活动时获得的最大收益。下面本文将对考虑互动行为的合作博弈模型的相关概念进行定义，并证明相关定理。

在第m轮谈判中，设局中人i提出的分配方案为表示局中人i给j分配的收益，分配方案应满足以下约束：

式（1）为分配方案的有效性约束，即联盟将收益全部分配给联盟成员。式（2）为分配方案的个体理性约束，即局中人的分配不小于自己单干或加入小联盟时的收益。所有局中人提出的分配方案构成了分配方案矩阵Xm：

在谈判过程中，局中人对某条分配方案的评价标准主要考虑两个要素，即个体最优信息和群体平均信息。

定义1个体最优信息体现了局中人对自己收益最大化的追求，局中人i的个体最优分配方案是在除了局中人i自己所提出的分配方案外的其他分配方案中，使局中人i收益最大的分配方案。即在第m轮谈判协商中，找出当前分配方案矩阵中对局中人i分配收益的最大值该最大值所在的分配方案为局中人i的个体最优分配方案，记为局中人对个体最优信息的学习表示为

定义2群体平均信息为联盟对局中人的收益分配的平均值，体现了联盟整体对个体的判断与偏好，即

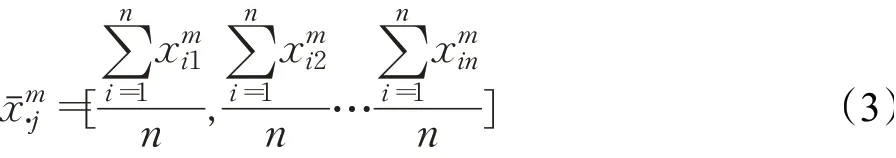
定义3分配方案的适应度定义为局中人对分配方案的满意程度，第i条分配方案的适应度为：

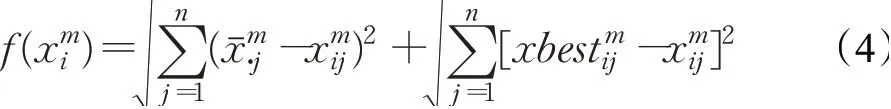
在谈判过程中，本文采用谈判档案作为局中人间的信息交流机制，从而实现局中人在谈判过程中的互动行为。采用这种非直接通信的方式好处在于当局中人的数目增加时，整个系统的通信开销的增幅较小，使得群体智能算法具有较好的扩展性。谈判档案的结构包括分配方案和适应度两个部分。谈判档案的构造过程为：通过适应度函数计算分配方案的适应度，按照适应度从小到大的顺序对分配方案排序，将分配方案和适应度存入谈判档案中。具体形式如图1所示。

图1 谈判档案结构Fig.1 Structure of solution archive

定义4群体最优信息为使联盟群体最满意的一条分配方案，即适应度最小的分配方案，也是谈判档案中第一条分配方案，记为局中人对个体最优信息的学习表示为

在现实博弈世界中，由于局中人在个体信息、形势判断、利益诉求等方面与理想状态存在差距，因此局中人在谈判过程中追求的是有限理性。在谈判过程中，局中人会对个体最优信息和群体最优信息进行一定程度的学习。本文使用理性因子来描述局中人的有限理性，使用控制因子来描述局中人对不同信息的学习程度。

定义6局中人的控制因子θm(θm∈[0,1])表示局中人对个体最优信息和群体最优信息的偏重程度，体现了不同谈判阶段局中人对个体最优和群体最优追求的变化。通常局中人在谈判前期更追求个体最优分配，在谈判后期为了维持联盟而更侧重群体最优分配。较大的控制因子可以提高全局搜索能力，避免陷入局部最优，较小的控制因子可以提高局部开发能力，从而加快收敛速度。控制因子的取值方式有线性策略和非线性策略两类，采用线性策略会使得控制因子在迭代过程中呈线性变化，易使收敛速度过慢和陷入局部最优，无法适应实际情况。本文采用一种反余弦的非线性策略来调整控制因子，基本思想是前期加快控制因子的改变速度，从而较快地进入局部搜索，避免陷入局部最优，后期通过较大的控制因子使算法更注重群体信息，保持解的多样性。反余弦控制因子构造方式如下：

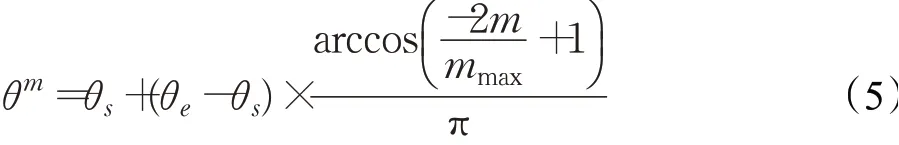
其中，mmax为预设的最大迭代次数，θs、θe表示控制因子的迭代初值和终值，在[0，1]范围内取值且θe＞θs。当0≤θm≤1/2时，局中人更加重视个体最优信息。当1/2＜θm≤1时，局中人更加重视群体最优信息。

控制因子随迭代次数变化曲线如图2所示。由图2可知，控制因子的变化幅度为[θs,θe]，当设定的θs＞1/2或θe＜1/2时，会导致算法只考虑一种最优信息，影响算法的收敛精度与速度，因此在设定参数时需保证θs＜1/2＜θe。

通过控制因子对迭代次数m求导可知控制因子的变化速度为：

因此，控制因子的变化速度与(θe-θs)同向变化，与mmax反向变化。为了避免陷入局部最优，前期加快控制因子的改变速度，(θe-θs)取值不宜过小，mmax取值不宜过大。

综合群体最优信息和个体最优信息，局中人采用混合策略调整分配方案，局中人在第m轮谈判的调整值为：

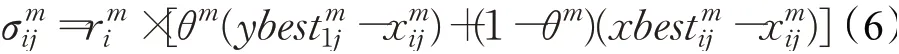
局中人在m轮谈判后的分配方案为：

定理1谈判过程中分配方案始终满足有效性约束。

∴谈判过程中分配方案始终满足有效性约束。

定理2谈判过程中分配方案始终满足个体理性约束。

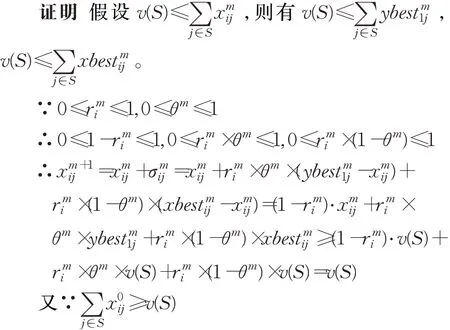
∴谈判过程中分配方案始终满足个体理性约束。

2 合作博弈的连续蚁群算法求解

连续蚁群算法是由Socha和Dorigo提出的一种用于求解连续变量组合优化问题的智能优化算法[18]，这种算法具有局部搜索能力强，收敛速度快等特点，目前已被许多学者应用到现实中的优化问题之中。针对原始连续蚁群算法寻优能力差、易陷入局部最优等问题，许多学者从不同角度提出了改进方案。Mahamed等引入Lévy分布和随机游走选择机制提高了算法的全局搜索能力，避免了早熟[19]。夏媛等提出了一种基于跨邻域搜索的改进连续蚁群算法，提高了算法的寻优能力和稳定性[20]。Can等将人工蜂群算法和遗传算法与连续蚁群算法相结合，提高了算法的性能[21]。本文将对原始连续蚁群算法进行改进，引入理性因子与控制因子，并将其应用于合作博弈的求解之中。

在使用连续蚁群算法求解联盟的收益分配问题时，将联盟中的局中人视为一群蚂蚁，蚂蚁的爬行路径视为该局中人的分配方案，该路径上每个维度的值相当于对不同局中人分配的收益。每轮谈判后蚂蚁会根据个体最优信息和群体最优信息有偏向地调整自己前行的路径，蚂蚁对路径的调整映射为局中人对分配方案的调整。理性的局中人既希望能达成共同接受的分配方案，又希望达成对自己效用最大的分配方案，既有共同目标，又有个体目标。在计算过程中，群体最优信息体现出群体的共同目标，个体最优信息体现出个体的不同目标，不断调整局中人对两种信息的学习程度体现了局中人选择策略规则的变化。随着不断迭代调整，所有蚂蚁汇聚在同一条路径上，所有分配方案的适应度相等且取得最小值0，这条路径所对应的分配方案即为被所有局中人接受的分配方案。

合作博弈的连续蚁群算法分为六步，具体求解步骤如下：

步骤1设置算法参数。设置理性因子、最大迭代次数、控制因子的初值和终值等初始参数。

步骤2所有局中人提出初始分配方案，为了使各局中人不会因为对分配方案不满而退出联盟，局中人提出的分配方案必须满足个体理性和有效性。所有分配方案构成了分配方案矩阵X0。

步骤3计算分配方案的适应度，排序后存入谈判档案中。通过式（4）计算分配方案的适应度，按照适应度从小到大的顺序对分配方案进行排序，将排序后的分配方案存储在谈判档案中，此时谈判档案中分配方案的适应度满足，根据谈判档案计算个体最优信息和群体最优信息。

步骤4判断谈判档案中分配方案的适应度是否相等且为0。若是，此时谈判档案中所有分配方案相同，得到最优分配方案，迭代结束。否则，进入下一步。

步骤5判断是否达到预设的最大迭代次数。若达到最大迭代次数，无法取得令所有局中人都满意的最优分配方案，停止迭代，输出谈判档案；否则，进入下一步。

步骤6构建新的分配方案。根据当前的个体最优信息和群体最优信息调整谈判档案中的分配方案，通过式（6）计算局中人的调整值，通过式（7）计算局中人的调整后的分配方案。转至步骤3。

合作博弈的连续蚁群算法求解流程如图3所示。

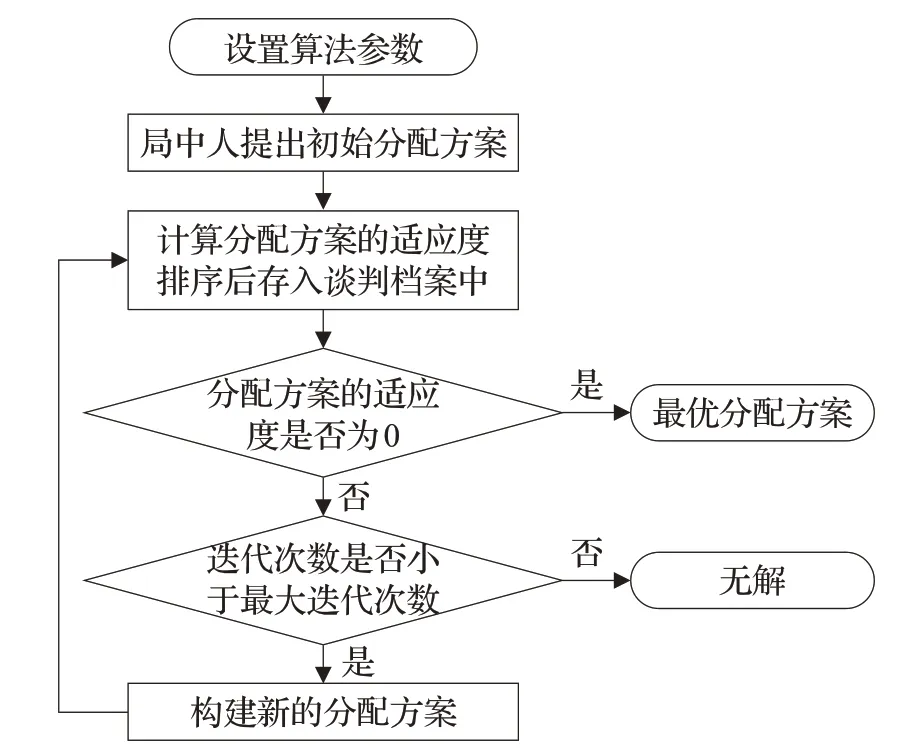
图3 求解流程图Fig.3 Solving process

3 算例分析

三家企业决定建立联盟生产某种产品投入市场，单独生产的收益为r1=1 200,r2=2 000,r3=900。两两合作生产的收益为r12=3 500,r13=1 600,r23=3 300。三家企业合作生产的收益为r123=4 540。当三家企业结成联盟合作进行生产时，应如何分配联盟的收益。

3.1 Shapley值法求解

Shapley值是目前应用最广的合作博弈解概念，它根据局中人i对联盟S的边际贡献来确定对局中人i分配的收益，具体计算方式为：

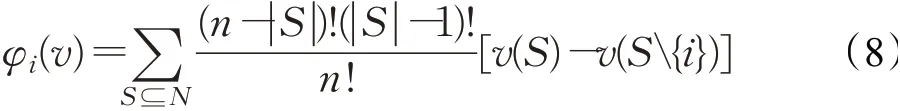
Shapley值法是一种衡量局中人边际贡献的均值方法，体现了分配方式的公平性，但对于非凸博弈来说，不能保证联盟的稳定性（即不能保证满足联盟个体和子联盟的合理性）。在本例中，由Shapley值计算得到局中人1的分配为1 180，小于其单干时的收益1 200，因此联盟会由于局中人1的退出而破裂。

3.2 改进连续蚁群算法求解

三家企业通过谈判来分配收益。将连续蚁群算法的参数设置为理性因子在[0，1]范围内随机取值，最大迭代次数mmax=500，控制因子初值θs=0，终值θe=1。

设企业i提出的分配方案为xi=(xi1,xi2,xi3)，各企业提出的分配方案需要满足个体理性和有效性：

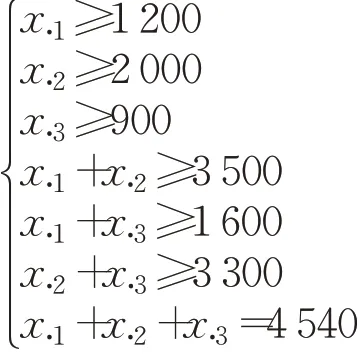
其中，x·j表示分配方案对企业j的分配。三家企业根据自身的偏好在约束条件下提出各自的初始分配方案，形成初始分配方案矩阵：

根据式（4）计算各分配方案的适应度，按照适应度从小到大的顺序将分配方案存入谈判档案中，谈判档案的形式为：

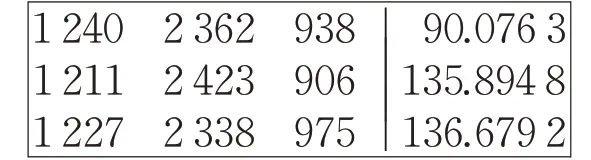
第一次谈判后各分配方案的适应度不等于0，迭代次数未达到预设的最大迭代次数。进入下一轮谈判，依次循环迭代134次，各分配方案的适应度函数为0，谈判档案中的分配方案不再变化，求解得到的最终谈判档案为：

图4 给出了谈判档案中适应度最小的分配方案的适应度的收敛曲线图。结果表明，适应度随迭代次数不断收敛，在迭代134次后趋于平稳，三家企业的最终分配方案为[1 234.463 4，2 366.176 7，939.359 9]。

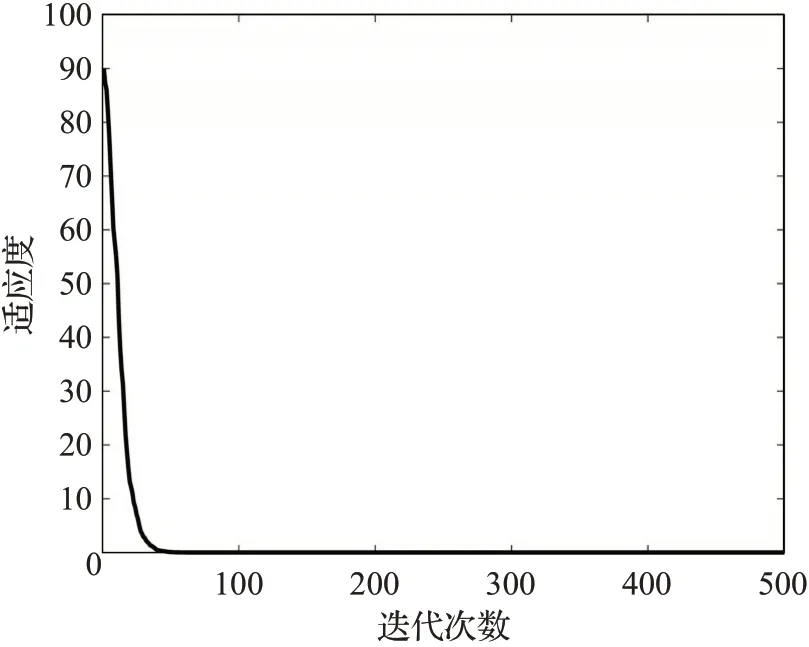
图4 适应度随迭代次数收敛图Fig.4 Value of optimal objective function varying with iteration times

算例表明：连续域蚁群算法经过多次迭代后，谈判档案中的分配方案趋于一致并不再变化，即联盟成员经过多次谈判可以得到一条使全体成员都满意的分配方案，且该分配方案满足个体理性和有效性。

3.3 实验结果分析

为增加对比性，分析本文算法有效性，采用MATLAB R2018a进行仿真实验，对原始连续蚁群算法和文献[20]基于跨邻域搜索的连续蚁群算法与本文改进后的算法进行分析对比，得出以下实验结果。各算法的适应度收敛曲线如图5所示。各算法实验数据如表1所示。

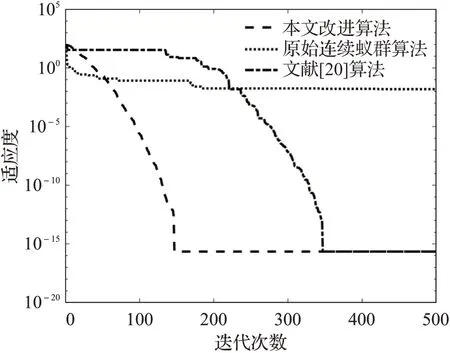
图5 不同算法收敛曲线对比图Fig.5 Comparison of convergence curves of different algrithms

表1 3种算法的实验数据Table 1 Experimental data of 3 algorithms

实验结果表明，在求解合作博弈问题时，相较于其他两种算法，本文提出的改进算法跳出局部极值的能力强，收敛速度快，收敛精度高。相较于原始连续蚁群算法易陷入局部最优，收敛速度慢，收敛精度低等缺点，本文提出的考虑互动行为等改进策略可以明显提高算法的性能。

4 结束语

目前，合作博弈在理论研究和解概念的数量上取得了巨大发展，但有效的现实应用依然偏少。产生这种情况的原因很多，其中一个根本性原因是没有考虑现实博弈环境中联盟分配方案的形成过程。这是目前合作博弈研究中被忽略的研究领域，但也是一个非常有潜力且与现实中的合作问题更加契合的研究领域。考虑到现实中合作收益（成本、风险等）的分配方案通常是经过多轮的谈判形成的，本文基于策略博弈理论和优化思想将合作博弈求解处理为基于个体博弈与群体趋同的多目标优化问题，引入了理性因子和现实因子构建考虑互动行为的合作博弈求解模型，提出了合作博弈的连续蚁群优化算法对合作博弈进行求解。相比合作博弈的经典解概念，这种求解思路与方法可以更好地描述局中人之间的互动决策行为，更加符合现实中自然人的博弈过程。这为求解合作博弈提供了新的思路与方法，对现实中人们描述、分析和预测联盟分配时具有决策支持作用。