开孔双层穹顶网壳结构的稳定性分析

刘 娟，杨 宁，孙 韬

(1.江苏建筑职业技术学院 建筑建造学院，江苏 徐州 221116；2.徐州市新型建筑工业化与信息化工程研究中心，江苏 徐州 221116；3.建筑工业化与信息应用技术研究所，江苏 徐州 221116；4.山东科技大学 山东省土木工程防灾减灾重点实验室，山东 青岛 266590；5.江苏建筑节能与建造技术协同创新中心，江苏 徐州 221116)

网壳是大跨空间结构中较为常见的一种结构体系，其稳定问题向来是结构设计的关键，有学者对国内外发生的109起典型钢结构事故进行统计，因稳定问题导致的事故占据比例最高，约达事故总数的33%[1]。而网壳结构通常耗资巨大，一旦出现失稳等突然性破坏造成的毁伤都是极其严重的[2]。20世纪80—90年代，各研究者从多个方面研究网壳的稳定承载力，期间收获了丰硕的成果[3]，但比较集中于网壳的弹性稳定分析。近几年国内陈昕等[4]、曹正罡[5]、李亚明等[6]、范峰等[7]对于空间结构稳定性做出了系统且深入的研究，但其考虑的跨度多为小、中跨度空间结构，而干煤棚、水泥熟料厂等工程中广泛采用的球面穹顶网壳通常为大跨度甚至超大跨度，且往往为满足使用要求而需开设孔洞，所开设的不对称孔洞无疑会破坏网壳原有的传力路径，并对网壳的承载性能产生不利影响。因此，对大跨度开孔穹顶网壳结构受力及弹塑性稳定分析展开研究，了解大跨开孔穹顶网壳结构的屈曲模态、屈曲前后结构的几何外形、杆件弯曲和变形等情况，对网壳的构造措施、网壳的选型及优化具有重要意义。

大跨度网壳对支座节点具有较高的要求，而不同的支座约束将会对穹顶网壳的结构刚度及稳定承载力产生影响，因此，本文通过数值分析研究该类大跨度开孔双层穹顶网壳分别在固定铰支座约束、弹性约束及固定约束的稳定承载能力，为类似工程的支座选型与设计提供参考。

1 工程概况及有限元模型建立

1.1 工程概况

某水泥厂石化均化库结构形式为落地双层正放四角锥球面网壳，根据生产工艺要求，网壳侧部开有孔洞，见图1、图2。网壳跨度87.00 m，厚度2.71 m，矢高29.21 m，网壳下部采用隔点布置固定铰支座，共计36个支座。下部支承钢筋混凝土独立柱截面尺寸为400 mm×600 mm，柱高10 m，混凝土强度等级C30。杆件选用GB/T 700—2006[8]中的Q235B钢，规格为φ45×3.5、φ65×3.5、φ75.5×3.75、φ88.5×4、φ114×4、φ140×4、φ159×6、φ168×6共8种截面。结构安全等级为二级，重要性系数取1.0。

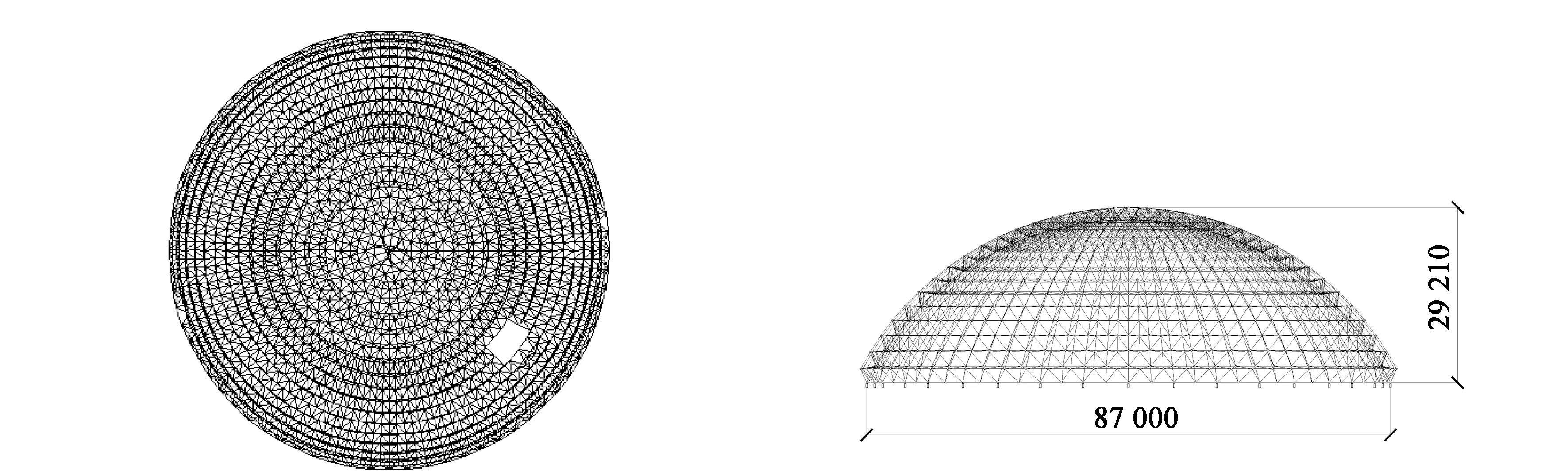
图1 模型俯视图 图2 模型侧视图

1.2 网格划分及孔洞开设位置

该双层穹顶网壳上弦设置17环，下弦设置18环，孔洞开设在第10环和11环，径向和环向各跨越两排杆件，上弦占9个网格(见图3)，下弦占12个网格。其水平投影(网壳上弦)面积为58.71 m2，洞口切平面投影(网壳上弦)面积为75.28 m2，孔洞投影尺寸见图4。

图3 上弦俯视图 图4 孔洞切面投影(mm)

1.3 荷载信息

(1)屋面为非上人屋面，设计活荷载为0.50 kN/m2；

(2)屋面恒荷载为0.30 kN/m2；

(3)屋面积灰荷载为0.80 kN/m2；

(4)抗震设防烈度为Ⅵ度，设计基本加速度值为0.05g，设计抗震第一组，场地土类别为Ⅱ类；

(5)基本风压取ω0=0.4 kN/m2，地面粗糙度为B类。

建模时采用LINK8单元模拟，并假定网壳节点为空间铰接节点，杆件只承受轴力；荷载均按静力等效原则化为作用于节点上的集中荷载，满跨均布荷载(见图5)，采用活荷载控制下的基本荷载组合[9]：

图5 荷载分布图

对于永久荷载的分项系数，取γG=1.2；对于可变荷载的分项系数，取γQ1=1.4。

2 特征值屈曲分析

特征值屈曲分析用于预测一个理想弹性结构的理论屈曲强度，可以初步确定结构的欧拉临界荷载，得到前几阶的屈曲模态。在分析时首先将网壳结构离散化，以网壳的各个杆件为基本元素，采用空间铰接杆单元。通过分析计算得到该网壳结构的特征值屈曲荷载为97.4 kN/m2，也就是该网壳结构的理论屈曲荷载。网壳结构的前三阶屈曲模态如图6所示。

从图6中可以看出，在主肋上，结构第一阶模态在孔洞上边缘区域竖向位移较大，该区域首先失稳。第二阶模态发生关于中心的不完全对称失稳，孔洞附近竖向位移较对侧竖向位移大。第三阶模态中，孔洞附近竖向位移依然较大，整个结构呈现两处凹陷和两处突起的失稳形态。

(a)一阶模态 (b)二阶模态 (c)三阶模态图6 双层网壳结构屈曲模态

3 稳定性分析

本网壳工程矢跨比为1/3，且开有孔洞，按《空间网格结构技术规程 JGJ 7—2010》的规定，需对该网壳结构进行稳定性能分析[10]。而双层穹顶网壳对初始缺陷比较敏感，故在ANSYS建模时按照一致缺陷模态法引入初始几何缺陷(节点的初始安装偏差)，图6中第一阶模态作为初始几何缺陷分布，最大缺陷值取结构跨度的1/300(即290 mm)，同时考虑材料非线性来研究结构的整体稳定性。

网壳结构对边界条件的要求比较高，其支座节点是网壳结构的重要构件，是网壳结构与下部支承结构的连接纽带。通常情况下，随着网壳跨度的增大，支座反力也相应的增大，本网壳跨度为87 m，属于大跨度网壳结构，支座节点将承受较大的支座反力，运用有限元软件ANSYS来研究该开孔双层穹顶网壳的非线性稳定分析[11]，进一步探索支座约束对其稳定承载力的影响规律。

3.1 固定铰支座约束条件下的网壳稳定性分析

网壳在失稳时各区域上下弦杆件形态变化基本一致，且网壳的失稳通常首先发生在主肋节点上，为简化分析，对网壳上弦网格编号如图7所示，结构共包含9肋、17环，孔洞位于第9条主肋上。绘制各主肋节点荷载-位移曲线，竖直向下位移为正，见图8—图15。

图7 网壳上弦编号图

图8—图15的(a)图分别为网壳1—8号主肋上1—13环节点在满跨荷载作用下的荷载-位移曲线。图8—图15的(b)图分别为各主肋14—17环各节点在满跨荷载作用下的荷载-位移曲线。对比以上各图不难发现，环号相同的各节点屈曲路径关于开孔洞主肋节点对称，即1号和8号主肋、2号和7号主肋、3号和6号主肋、4号和5号主肋的屈曲形态基本相同。

观察图8—图15的(a)图可以发现，在加载前期，随着环号(1—13)的增加，结构刚度在逐渐增大。环号相同的各主肋节点，加载前期的荷载-位移曲线斜率差异较小，即开设孔洞对同环的结构刚度影响较小。

在图8—图15的(b)图中，在加载前期，随着环号(14—17)的增大，各节点荷载-位移曲线斜率呈不规则变化，但都小于上一环同荷载段斜率。各主肋首先失稳的节点也出现在这几环当中。在接近极限荷载阶段，节点所属环号越小，其荷载位移关系的非线性越强。在同一环当中，当环号不超过10时，4号和5号主肋节点荷载位移关系非线性最强，2号和7号肋荷载-位移关系非线性最弱；当环号大于10时，在达到极限荷载之前，荷载位移基本呈线性关系，在达到极限荷载时节点产生的位移较小，节点瞬间失稳。

结合图8至图15，除第2号和7号主肋在第15环首先发生失稳。其余各主肋均在第16环首先发生失稳。这也表明，荷载位移曲线表现出的非线性关系越弱，就越容易发生突然失稳。在靠近孔洞的1号和8号主肋，第3—10环各节点在屈曲后仍具有一定的承载能力。这是由于在设计过程中，此部分杆件有所加强的缘故。

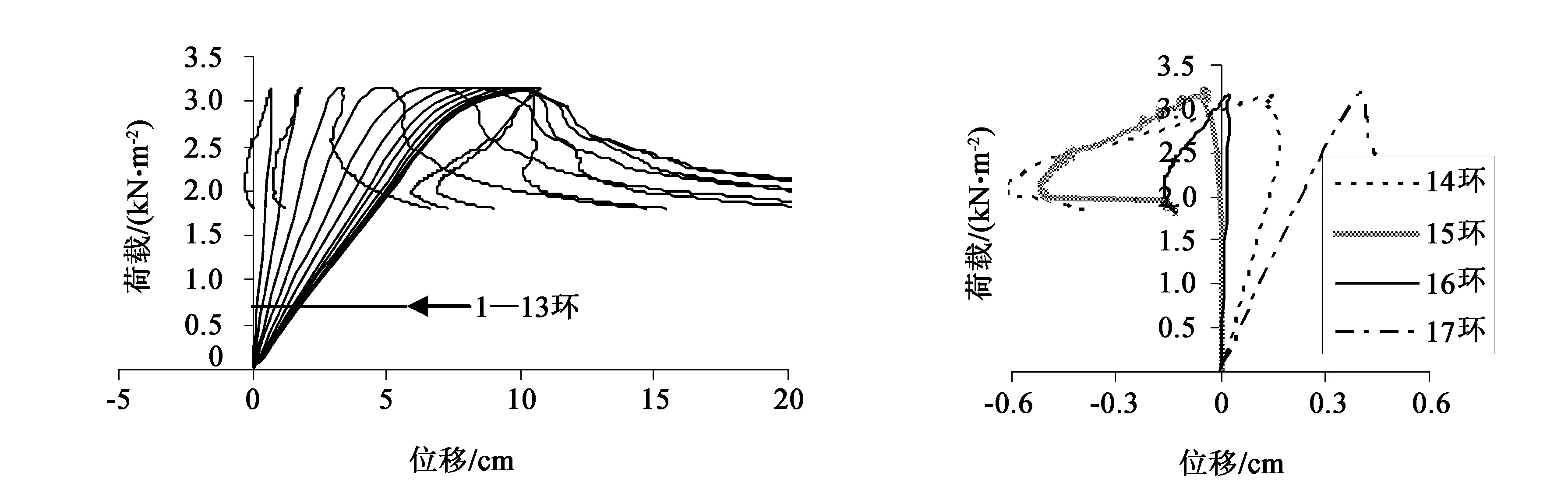
(a)1—13环 (b)14—17环图8 1号主肋各节点荷载-位移曲线

(a)1—13环 (b)14—17环图9 2号主肋各节点荷载-位移曲线

(a)1—13环 (b)14—17环图10 3号主肋各节点荷载-位移曲线

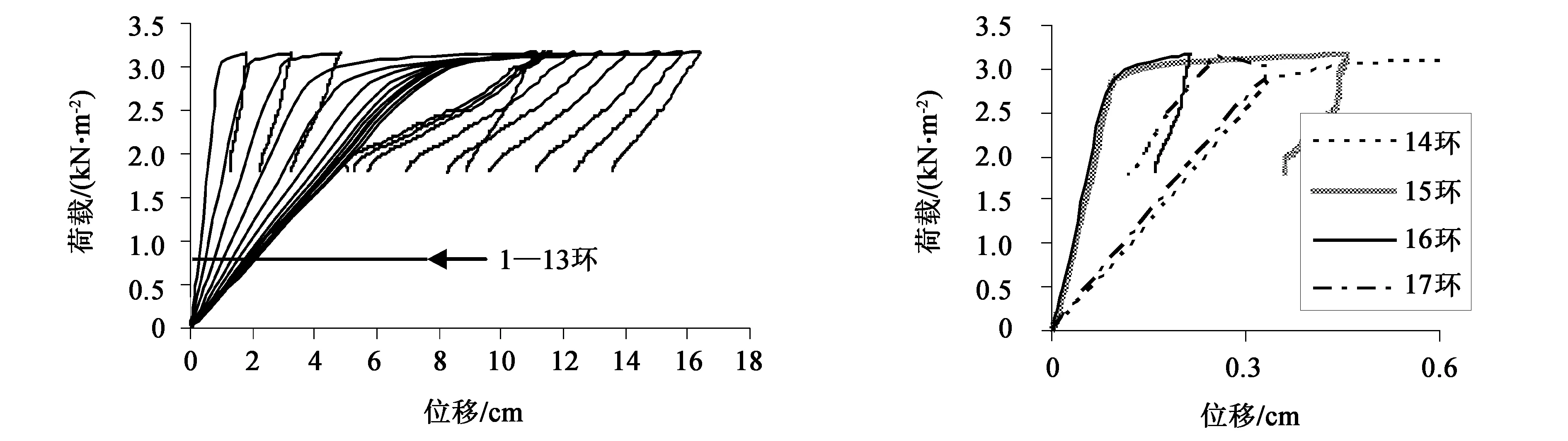
(a)1—13环 (b)14—17环图11 4号主肋各节点荷载-位移曲线

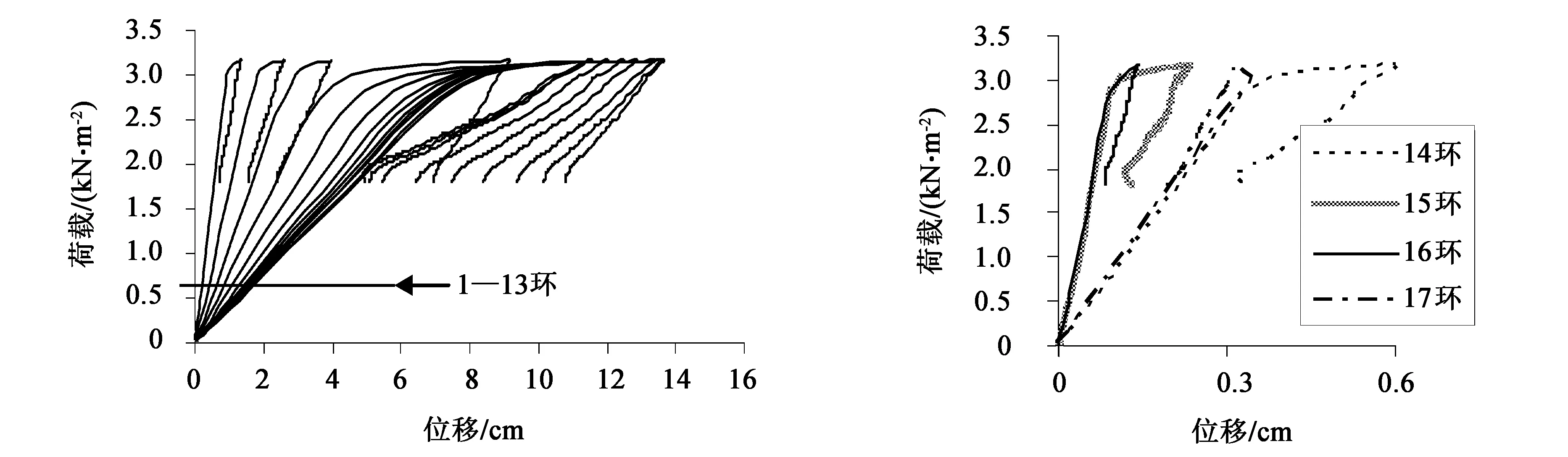
(a)1—13环 (b)14—17环图12 5号主肋各节点荷载-位移曲线

(a)1—13环 (b)14—17环图13 6号主肋各节点荷载-位移曲线

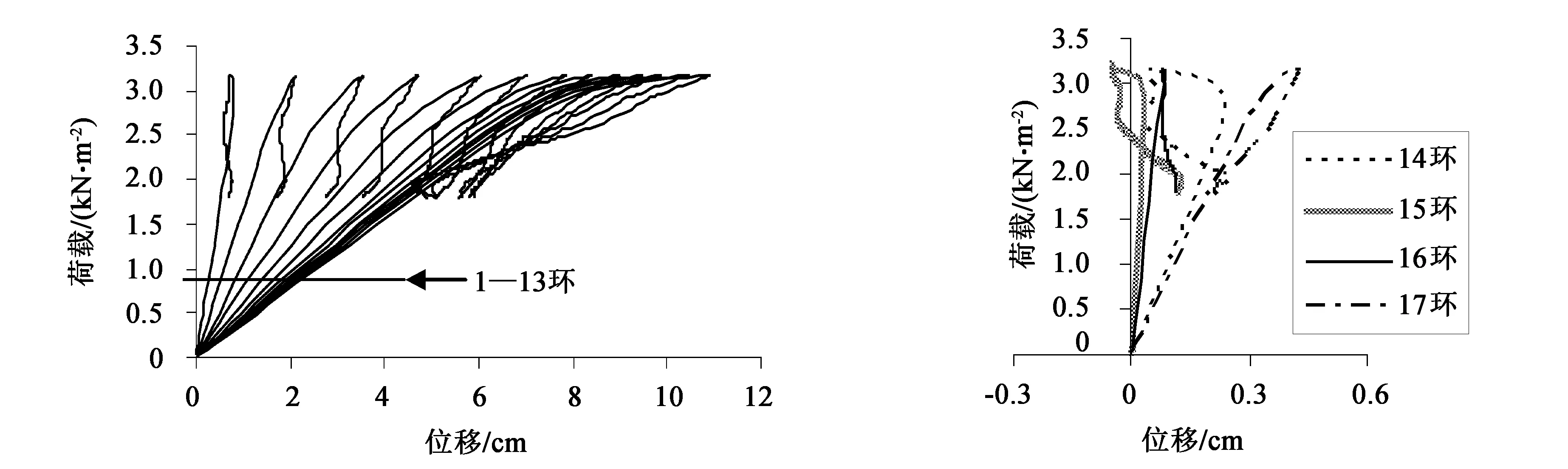
(a)1—13环 (b)14—17环图14 7号主肋各节点荷载-位移曲线

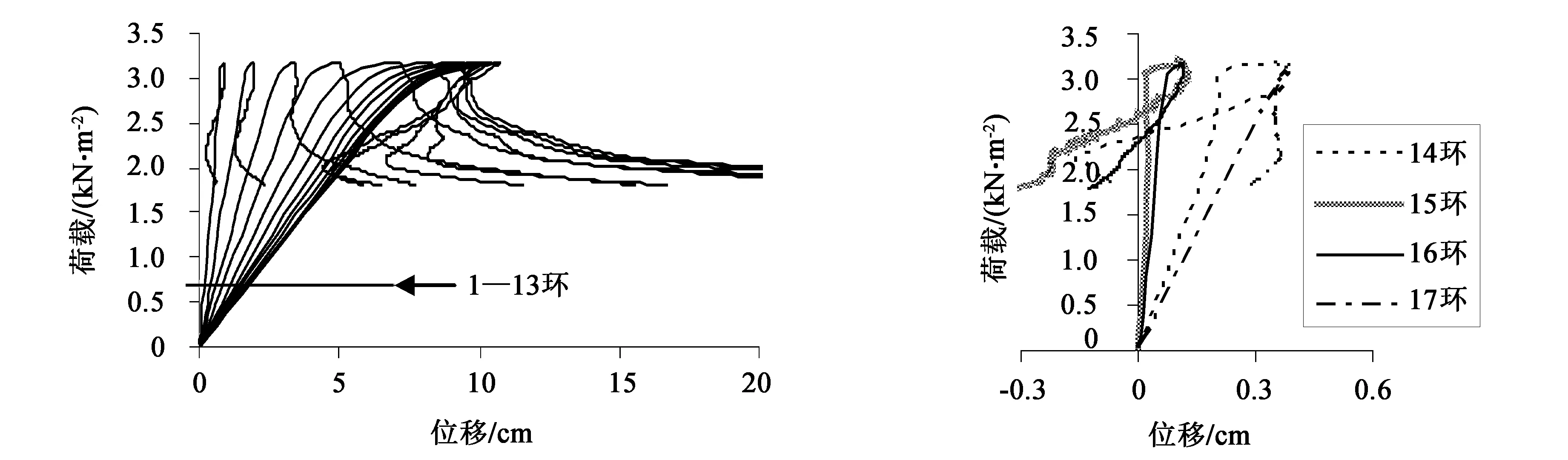
(a)1—13环 (b)14—17环图15 8号主肋各节点荷载-位移曲线

图16为9号主肋(即开孔洞主肋)上各节点荷载-位移曲线，由于开设孔洞，第9号主肋缺少第10环和11环节点，杆件间断。

由图16(a)可以看到，节点所属环号越大，其屈曲后承载力越强，变形也越大。观察孔洞下方节点屈曲路径，曲线斜率在加载前期较孔洞上方节点明显增大，表明开设孔洞减小了孔洞上方结构刚度，即在荷载作用下，孔洞上方节点将产生较大的位移。

(a)1—9、12、13环 (b)14—17环图16 9号主肋各节点荷载-位移曲线

由图16(b)可以看到，在达到极限荷载以前，各节点荷载位移基本呈线性关系，各节点曲线斜率均大于第13环，第16环节点曲线斜率最大，在达到极限荷载时，结构即失去承载能力，节点瞬间失稳。第16环节点在达到极限荷载时位移最小，仅为3 mm，其加载前期斜率也最大，该环节点将是该主肋上最先失稳破坏的节点。

3.2 弹性水平约束条件下的稳定性分析

在固定铰支座情况下，本网壳工程静力计算得到的结构支座反力见表1。由表可知，网壳结构径向水平支座反力较大为250.3 kN，因此采用弹性约束更有利于上部结构与下部结构的协同工作。

表1 支座反力最大值

3.2.1 径向采用弹性约束

网壳支座竖向和切向采用固定约束，径向采用弹簧约束，建模时满跨荷载作用，水平支座刚度分别取100、300、500、700、1000 N/mm和固定铰支座(刚度无穷大)6种情况。

图17为6种支座刚度情况下竖向位移最大节点的荷载-位移曲线。由图可以看出，在加载初期，各曲线荷载与位移几乎呈线性变化，随着径向水平支座刚度的减小，曲线斜率逐渐减小，即结构的刚度在逐渐降低，网壳的第一极限荷载也呈递减趋势，第二极限荷载与第一极限荷载的差值逐渐增大。也就是说，随着径向水平支座刚度的增大，网壳的屈曲后承载能力在逐渐减弱。各支座刚度情况下网壳的极限承载力见表2，在表中对各支座刚度情况下的极限荷载与固定铰支座约束条件下的极限荷载进行了对比，由此可见，支座刚度的强弱对网壳稳定承载力及屈曲后性能均有较大影响。

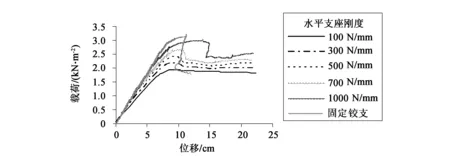
图17 径向为弹性支座时竖向位移最大节点的荷载-位移曲线

表2 径向为弹性时，水平支座刚度不同下的网壳极限承载力

3.2.2 切向与径向均采用弹性约束

网壳支座竖向采用固定约束，径向与切向采用弹簧约束，建模时满跨荷载作用，水平支座刚度分别取100、300、500、700、1000 N/mm和固定铰支座(刚度无穷大)6种情况。

图18为径向和切向均为弹性支座时竖向位移最大节点的荷载-位移曲线图。比较图17和图18，二者在相同弹簧刚度时的荷载-位移曲线形状非常相似，包括曲线刚度的变化规律和屈曲后路径变化规律，两者仅在极限承载能力上差异较大，详见表2。

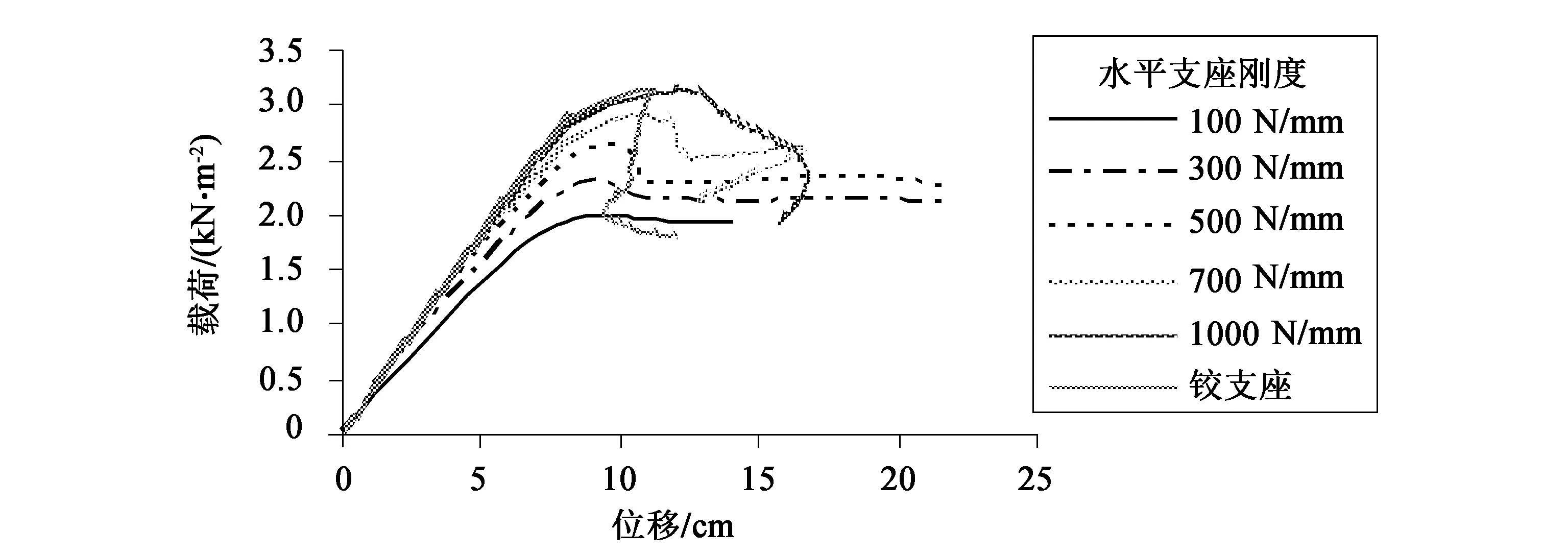
图18 径向和切向均为弹性支座时竖向位移最大节点的荷载-位移曲线

表3 径向和切向均为弹性时，水平支座刚度不同下的网壳极限承载力

图19为两种约束条件下极限荷载的直方图。可以看出，随着弹簧刚度的增大，双向弹性约束条件下极限荷载增加较快，在弹簧刚度大于700 N/mm后，极限荷载增加速度减慢。

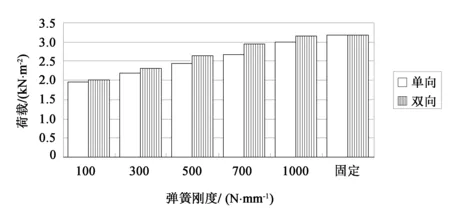
图19 单向与双向弹性约束极限荷载比较直方图

综上，采用固定约束的双层球壳结构整体稳定承载力较弹性约束时稳定承载力高，但径向与切向均采用弹性约束时，球壳结构整体稳定承载力较仅径向弹性约束时稳定承载力高。经过计算，以本网壳结构支座径向刚度取500 N/mm的条件下，单向弹性约束极限荷载为2.43 kN/m2，双向弹性约束极限荷载为2.64 kN/m2，分别较固定铰支座时极限荷载降低了23.1%和16.46%，由此可见，支座约束条件对网壳结构的影响是比较大的，且采用弹性支座约束时结构的屈曲后承载能力会有明显提高，这也表明，在弹性约束条件下，开孔洞网壳结构对初始缺陷的敏感性较小。

4 结论

通过对开孔双层网壳结构的非线性稳定计算和分析，总结其屈曲性能和破坏机理，对比固定铰支座约束、弹性水平约束时该网壳的非线性分析结果，得出以下结论：

(1)固定铰支座约束条件下开孔双层穹顶网壳结构的屈曲特点和规律：环号相同的各节点屈曲路径关于开孔洞主肋节点对称。在加载前期，孔洞上方各节点荷载位移基本呈线性关系，屈曲路径基本一致。在接近极限荷载一段，环号越大，其表现出的非线性越强，在达到极限荷载时的位移越大，屈曲后承载力越强，失稳越晚。孔洞下方节点曲线初始段斜率较孔洞上方节点有较大增加，即结构刚度有跳跃性变化。

(2)支座约束条件对开孔双层网壳结构的影响非常大，采用弹性支座时结构的屈曲后承载能力会有明显提高，并能够降低结构对初始缺陷的敏感性。