一类捕食者-食饵扩散模型的Hopf分支和Turing分支

吴耀冲，温洁嫦

(广东工业大学 应用数学学院，广东 广州 510520)

捕食者-食饵模型是生物数学的一个重要分支，是研究种群与种群以及环境与种群之间联系和影响的科学。在20世纪20年代，意大利数学家Volterra提出著名的Lotka-Volterra系统之后，国内外对捕食者食饵模型的研究越来越深入。考虑到人类活动对种群的影响以及合理利用生物资源，对模型加入收获率具有深刻意义，如文献[1-5]研究了捕食者具有收获率的捕食者食饵模型。随着研究的深入，模型越来越考虑到更多的实际情况，研究人员注意到由于种群的分布空间是不均匀的，而且捕食者更喜欢活动在容易捕获到食饵的区域，同时食饵则尽可能地逃脱捕食者的追捕，于是，在对模型的研究中，要考虑到物种的空间移动，便引入了扩散的概念。文献[6]用反应扩散系统说明了许多典型的斑图模型，而文献[7-11]研究了具有扩散项的捕食者-食饵模型。早在1983年Macdonald[12]发现合作捕猎是许多生态系统中普遍存在的行为，例如狮子[13]、狼[14]、非洲的野狗[15]、蚂蚁[16]等。文献[17]分析了一种捕食者食饵模型，将其推广到合作狩猎之中，并发现狩猎合作对捕食者食饵系统稳定性具有影响。所以合作捕猎对两种群的系统的影响也应被考虑到。受文献[17-18]的启发，本文提出以下系统模型：

(1)

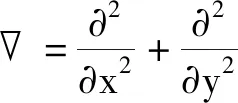
1 系统稳定性和分支分析

首先，讨论模型(1)对应的常微分系统：

(2)

考虑到模型的实际背景，本文只讨论模型(1)和(2)的非负平衡点。

通过计算易得到，系统(2)有3个平衡点，分别为平凡平衡点E0=(0,0)、边界平衡点E1=(k,0)和一个正平衡点E2=(u*,v*),其中

(3)

v*3+b*v*2+c*v*2+d=0,

(4)

(5)

(6)

(7)

定理1 平衡点E0是不稳定的鞍点。

证明系统在平凡平衡点E0=(0,0)处的Jacobi矩阵

(8)

矩阵J0的特征根分别为λ1=r>0,λ2=-m-e2<0,故平衡点E0是不稳定的鞍点。

定理2 当e1λk-m-e2<0时，D(J1)>0,-T(J1)>0,此时E1局部渐近稳定；当e1λk-m-e2>0时，D(J1)<0,此时E1不稳定。

证明系统在边界平衡点E1=(k,0)的Jacobi矩阵为

(9)

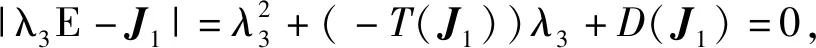
①当e1λk-m-e2<0时，D(J1)>0,-T(J1)>0,此时E1局部渐近稳定；

②当e1λk-m-e2>0时，D(J1)<0,此时E1不稳定。

定理3 当r-ke1av*>0,(2av*+λ)ke1(av*+λ)2-ra(m+e2)>0时，正平衡点E2渐近稳定。

证明系统在正平衡点E2=(u*,v*)处的Jacobi矩阵为

(10)

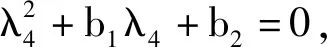
(11)

(12)

所以平衡点E2=(u*,v*)是渐近稳定的,当且仅当以下不等式成立:r-ke1av*>0,(2av*+λ)ke1(av*+λ)2-ra(m+e2)>0。

定理4 当rH=ke1av*时，系统(2)发生Hopf分支。

证明由以上讨论可知，

(13)

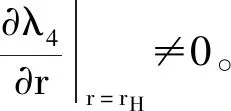
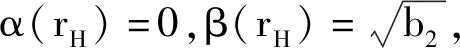
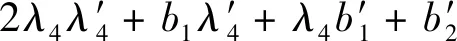
(14)

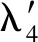
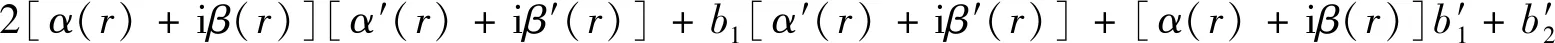
整理得

2[α(r)α′(r)+iα(r)β′(r)+iβ(r)α′(r)-β(r)β′(r)]+

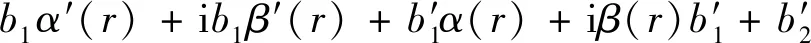
分离实部和虚部，得

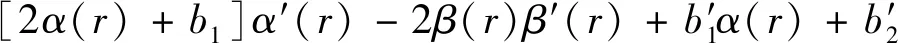
(15)

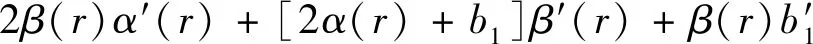
(16)

令

P1(r)=2α(r)+b1,

(17)

P2(r)=2β(r),

(18)

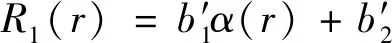
(19)

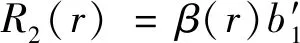
(20)

则式(15)、(16)变为

P1(r)α′(r)-P2(r)β′(r)+R1(r)=0,

(21)

P2(r)α′(r)+P1(r)β′(r)+R2(r)=0 ,

(22)

所以

(23)

将r-rH代入式(17)—(20)，有

P1(rH)=b1=0,

(24)

(25)

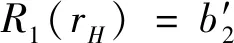
(26)

(27)

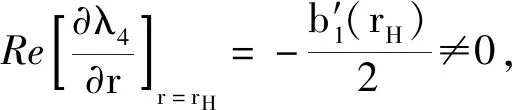
下面讨论Hopf分支方向。

令w1=u-u*,w2=v-v*,系统(2)变为

(28)

令

ξ=e1(av*+λ)v*w1+e1au*v*w2,η=-w0w2，

(29)

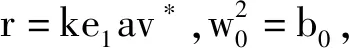
(30)

其中

(31)

(32)

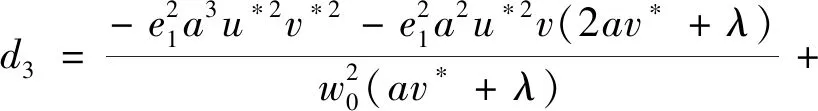
(33)

(34)

(35)

引入复变量z=ξ+iη，则

(36)

有

i(3aλv*2w0+λ2v*w0+2a2v3w0-ae1λu*v*w0-4a2e1u*v*2w0)],

(37)

(38)

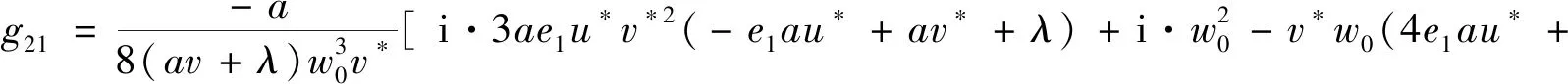
av*+λ)]。

(39)

一阶Lyapunov系数公式[19]：

(40)

所以，当l(0)<0时,系统(2)在正平衡点附近产生超临界的Hopf分支；当l(0)>0时,系统(2)在正平衡点附近产生次临界的Hopf分支。

下面讨论带扩散的捕食者食饵模型即模型(1),只考虑正平衡点E2附近的动力学性质。作平衡态附近的扰动：

(41)

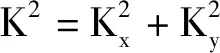
|J2-K2D-λE|=0,

(42)

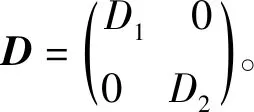
将式(42)展开，得

λ2+C1(K2)λ+C2(K2)=0,

(43)

其中

(44)

C2(K2)=h1K4+h2K2+h3,

(45)

h1=D1D2,

(46)

(47)

(48)

定理5 当D1>D2时,系统发生Turing失稳。

证明根据文献[20]知道,系统(1)产生Turing不稳定需要以下条件

由系统(2)在正平衡点附近稳定知,r>ke1av*，故

所以要使h2<0，当且仅当D1>D2。这表明在系统(1)中，若扩散导致系统的不稳定，只有当食饵的扩散速度大于捕食者的扩散速度才有可能发生。

2 数值模拟

上述分别分析了非扩散系统(2)在平衡点E1附近，食饵出生率和环境容纳量对系统稳定性的影响。在k=25条件下，分别对r=0.2、0.8时，绘制平衡点E1附近的轨线图及种群密度随时间变化图，如图1—图4所示。从图中容易发现两物种紧密地相互依存，但提高食饵的出生率并不能影响整个系统稳定性，系统的轨线、捕食者和食饵的种群密度随时间的变化并没有发生改变，所以在这种情况下，要使食饵和捕食者长久稳定下，仅提高食饵的出生率效果并不显著。另外，当环境容纳量改变时(图5—图6)，刚开始时系统在E1附近很短的时间内，随着捕食者能量的摄入，捕食者数量增加，而食饵不断被捕杀呈递减状，但很快这种情况就发生了改变，捕食者数量急剧下降最终完全灭绝，同时由于天敌的消失，食饵数量小幅度上升之后长期稳定在固定的状态。对比图3、图5和图4、图6，可以得到结论：环境容纳量的改变，会影响系统(2)的稳定性，如森林火灾导致的栖息地减少，水资源污染等行为可能对生态系统产生巨大影响。

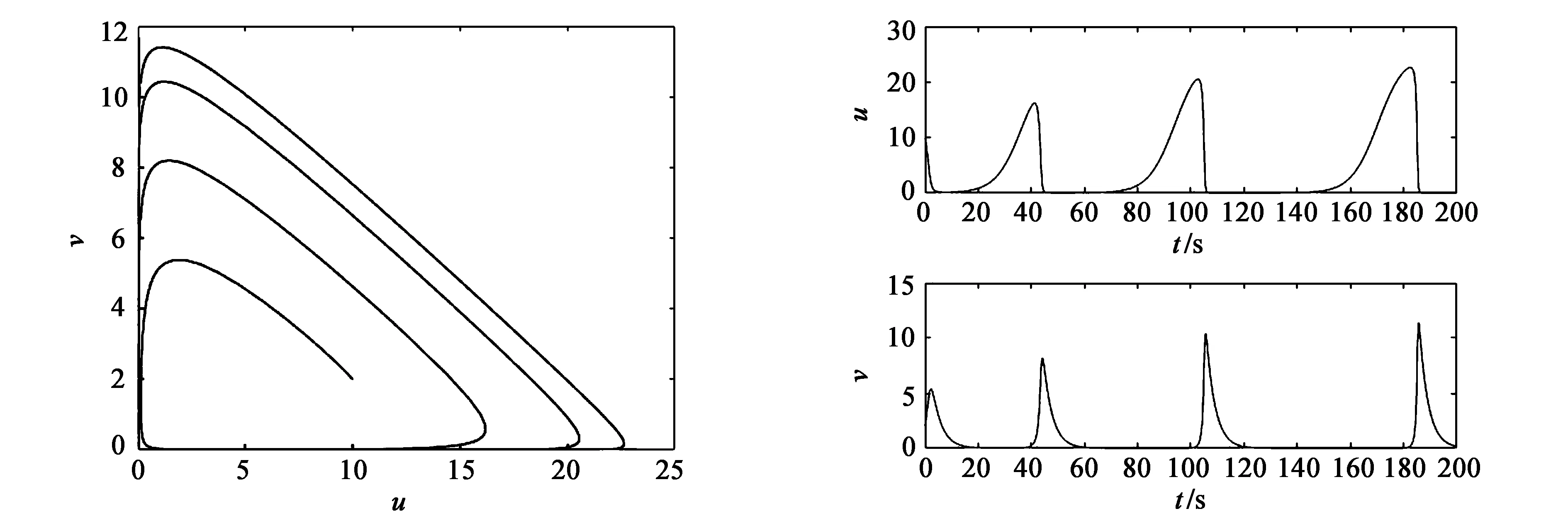
图1 k=25,r=0.2,E1附近的轨线图 图2 k=25,r=0.2,种群密度与时间关系

图3 k=25,r=0.8,E1附近的轨线图 图4 k=25,r=0.8,种群密度与时间关系

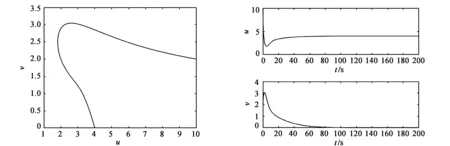
图5 k=4,r=0.8,E1附近的轨线图 图6 k=4,r=0.8,种群密度与时间关系

接下来分析非扩散系统(2)在平衡点E2附近，人类对捕食者的狩猎行为对两物种的影响。通过对比实验图7、图9和图8、图10，可看到：在相同的初始条件下，环境容纳量k=7时，随着线性收获系数e2的增大，系统在平衡点E2附近由稳定态变为不稳定态，而且随着捕获系数的增大，最终系统中的捕食者趋于灭绝。通过实验图11、图13和图12、图14可知，初始条件和前面保持一致，但改变环境容纳量k=17，从E2附近的轨线图和捕食者食饵的种群密度随时间关系可以发现：此时随着线性收获系数e2的增大，系统在平衡点E2附近却由不稳定态变为稳定态，而且捕食者和食饵在这种稳态下共存并没有灭绝。另外，在这种情况下，环境容纳量也会对系统的稳定性产生影响(图7和图11)。所以，我们可以得出以下结论：当环境容纳量较大时，恰当提高人类对捕食者的狩猎量将有利于该系统的稳定性；在环境容纳量较小时，要降低人类对捕食者的捕获量，防止因过渡捕捞而致使物种的灭绝。

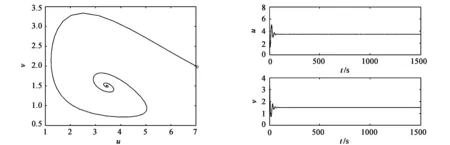
图7 k=7,e2=0.1，E2轨线图 图8 k=7,e2=0.1，种群密度与时间关系

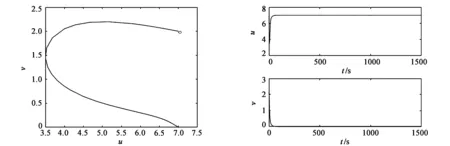
图9 k=7,e2=0.3,E2轨线图 图10 k=7,e2=0.3，种群密度与时间关系

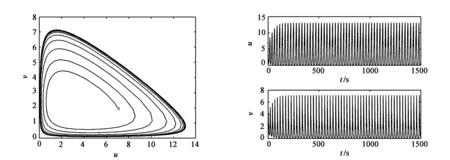
图11 k=17,e2=0.1,E2轨线 图12 k=17,e2=0.1，种群密度与时间关系

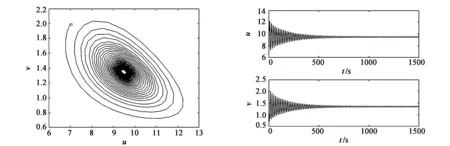
图13 k=17,e2=0.6，E2轨线 图14 k=17,e2=0.6，种群密度与时间关系

看Hopf分支图。取r为分支参数，k=12,a=0.03,λ=0.1,e1=0.6,m=0.2,e2=0.1,此时u*=3.132 255 6,v*=1.987 135,且l(0)<0，系统(2)在E2=(u*,v*)附近产生稳定的Hopf分支(图15—图16)。此时，捕食者与食饵种群密度呈周期性变化，长期稳定共存。

图15 取r为分支参数 图16 稳定的Hopf分支

下面对系统(1)的空间班图进行数值模拟。所有模拟均在400×400的格子内进行，空间间隔为1；模拟采用的是齐次Neumann边界条件。由于在空间分布上捕食者和食饵类似，所以本次只讨论食饵的Turing斑图，取k=25,e1=0.6,m=0.2,λ=0.1,r=0.4,D2=0.1,讨论捕获系数e2对Turing斑图形成的影响。

初始条件为种群的初始随机分布，扩散系数设为D1=6,图17—图19分别表示e2=0.1、0.3、0.7的情形。对比这3幅图可见，图17中斑图大部分是点状，有一小部分的条状，但图18的条状斑增多，在图19中条状斑图最多，但仍存在点状斑。所以，随着捕获系数的增大，虽然Turing斑图不相同，但斑图的结构却未发生变化。图20—图22分别表示D1=12，e2=0.1、0.3、0.7的情形。对比图17和图20,可以看到，在图20中，条状清晰可见且点状消失，图20—图22的Turing斑图结构未发生改变。

图17 e2=0.1，D1=6 图18 e2=0.3，D1=6 图19 e2=0.7，D1=6

图20 e2=0.1，D1=12 图21 e2=0.3，D1=12 图22 e2=0.7，D1=12

3 总结

本文讨论了一类捕食者带线性收获率和合作行为的捕食者食饵模型，从理论上讨论了非扩散系统的平衡点存在条件和稳定性，并且证明了系统(2)在r=rH时产生Hopf分支，还说明了扩散导致系统(1)失稳的条件。从数值模拟上验证了上述结论，并得出如下结论：

1)食饵的出生率会改变捕食者种群密度的峰值,但对系统稳定性影响不大；

2)环境容纳量会对系统稳定性产生巨大影响；

3)人为的捕获量的控制应根据环境容纳量做出调整，环境容纳量较大时，可以恰当提高人为捕获量，环境容纳量较小时，减少人为捕获且要防止种群趋于灭绝；

4)食饵的扩散速度和人为的捕获均对Turing斑图产生了影响,理论和实验的结果表明，系统(1)具有丰富的动力学行为。