基于变异系数和模糊集的活动轮廓图像分割模型

黄丽转，刘国军，魏立力

（宁夏大学数学统计学院，银川 750021）

引 言

图像分割在图像分析和计算机视觉中起着重要的作用，其目的是将特定图像划分为若干部分，通常每个部分在某一特征方面是均匀的，例如强度、颜色和纹理等。近年来，学者们提出了大量的图像分割算法来提高图像分割的精度和效率［1］。其中，活动轮廓模型（Active contour model，ACM）已成为图像分割领域的一个有效框架，通常可分为基于边缘的活动轮廓模型［2⁃3］和基于区域的活动轮廓模型［4⁃6］。基于边缘的活动轮廓模型使用梯度信息来引导不断变化的轮廓向目标边界移动，此类模型对初始轮廓比较敏感，不能提取弱边缘或模糊的目标。基于区域的活动轮廓模型根据图像区域信息处理，当演化曲线到达真实目标边界时能量达到极小值。作为Mumford⁃Shah（M⁃S）模型［6］的一个特殊实例，Chan⁃Vese（C⁃V）模型［4］是最具代表性的基于区域的ACM之一，该模型利用内外平均灰度值的差异而不是图像梯度来驱动演化曲线向边界运动。近几年，不少文献从不同方向对C⁃V模型进行改进［7⁃8］：Zhang等［9］提出一个基于图像全局信息的活动轮廓（Selective local or global segmentation，SLGS）模型，提高了分割速度，然而由于依赖图像的全局信息，对灰度不均匀图像的分割效果不理想；Li等［10］提出基于图像局部区域的可变灰度拟合（Region⁃scalable fitting，RSF）模型，克服了基于全局模型在灰度不均图像分割中的不足，但从分割结果中可以看出，过度依赖图像的局部信息使得该模型对初始化轮廓和噪声较为敏感。

为了解决基于区域的活动轮廓模型中能量泛函的最小化问题，通过将模糊集纳入活动轮廓模型，文献［11］首次提出了一种基于模糊能量的活动轮廓（Fuzzy energy⁃based active contour，FEAC）模型。之后，文献［12⁃14］提出了基于FEAC改进的模型，将局部图像信息纳入基于区域的ACM。全局和局部FEAC（Global and local FEAC，GL⁃FEAC）［12⁃14］模型中的局部能量泛函将局部空间信息和强度信息结合到ACM中，降低了图像中灰度不均匀性的影响。文献［15⁃16］将图像的核度量和形状先验等特征融合到FEAC模型中，提高了分割性能。但是，这些模型没有正则化项，导致演化曲线不光滑，无法保持伪水平集的距离特征。此外，通过逐像素计算曲线演化过程中能量函数的变化值来更新隶属度，大大增加了计算复杂度。更重要的是，分割的图像中若包含弱边缘和低对比度，可能会出现边界缺失问题。Fang等［1］提出了一种新的基于混合和局部模糊区域边缘的主动轮廓模型（Hybrid and local fuzzy region⁃edge based active contour model，HLFRA），可以成功地从高噪声和强度不均匀的合成图像和真实图像中提取目标边界。Ahmad等［17］首次提出将变异系数（Coef⁃ficient of variation，CoV）与模糊隶属函数相结合，可以分割具有较高噪声、强度不均匀的图像和弱纹理图像。

受文献［1，17］的启发，本文构建的新能量泛函包括区域能量和边缘能量。区域能量由基于变异系数的混合模糊区域项和局部模糊区域项组成，可以平衡目标和背景的重要性，驱使初始轮廓向目标边界移动，而结合了局部空间信息的局部模糊区域项可以降低图像强度不均匀性的影响。另外，边缘能量对伪水平集函数进行正则化，保持曲线演化过程中的平滑性。本文模型在分割有较高噪声以及混合噪声和弱纹理的图像时，不仅速度快，而且分割性能较其他模型好。

1 相关知识

1.1 FEAC模型

为了获得凸能量泛函，Krinidis等［11］将模糊思想引入ACM中，提出了FEAC模型。与流行的ACM不同，FEAC模型用0.5水平集作为演化曲线。伪水平集定义为

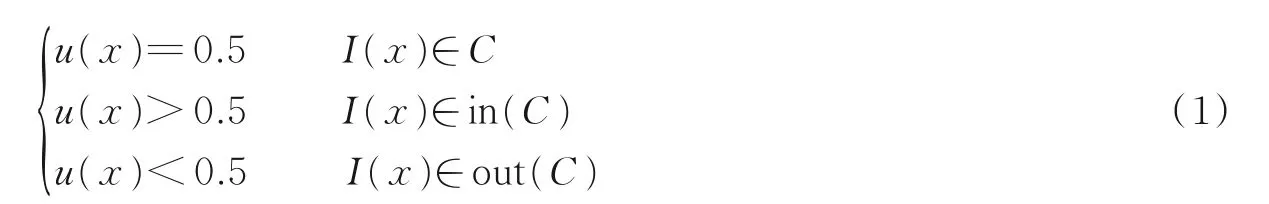
式中：I(x)为输入图像；in(C)和out(C)分别表示曲线C的内部和外部。式（1）定义的伪水平集将图像分割成两部分，其能量泛函定义为

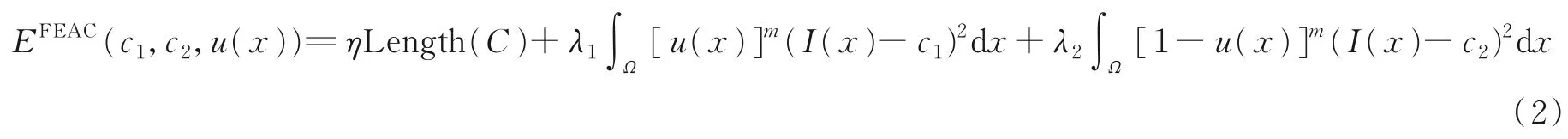
式中：常数η≥0，λ1>0，λ2>0为3个固定的参数；m为指数；Length（C）代表C的长度；c1和c2分别代表曲线内外部的图像的平均灰度值，保持u(x)不变，最小化式（2）可得

但是，FEAC模型中没有正则化项，导致演化曲线不光滑，无法保持伪水平集的距离特征。此外，通过逐像素计算曲线演化过程中能量函数的变化值来更新隶属度，大大增加了计算复杂度。更重要的是，当分割的图像边缘较弱、对比度较低时，可能会出现遗漏边界的问题。

1.2 HLFRA模型

HLFRA模型［1］与FEAC模型类似，演化曲线c由伪水平集表示，将图像分为两部分，能量泛函定义为

虽然HLFRA模型结合了图像的区域和边缘信息，但在分割具有弱边缘的图像时仍存在丢失边缘信息的情况，且对混合噪声的分割性能并不好。

1.3 Ali Ahmad模型

变异系数可称为信号的相对标准差，定义为SD mean，它可以被认为是对给定观测数据的离散度（变异）的规范化测量。Ahmad等［17］提出了一种基于变异系数的数据拟合项模型（Ali Ahmad模型）来处理真实图像的空间异质性。此外，模型采用模糊隶属度函数表示图像中每个像素对于前景或背景中的隶属度。为了降低模型的计算量，用高斯滤波代替长度项，它能更好地拟合非均匀图像中的数据。对于给定的图像I0，定义图像域Ω，Ali Ahmad模型［17］的能量泛函为

式中：λ1、λ2、μ均为正常数；m为权重指数，文中取m=2；0≤v(z)≤1为度量一个像素属于曲线C内的隶属度，1-v(z)度量一个像素属于曲线C外的隶属度，v1(z)和v2(z)分别表示曲线C内部和外部的平均灰度值，表达式为

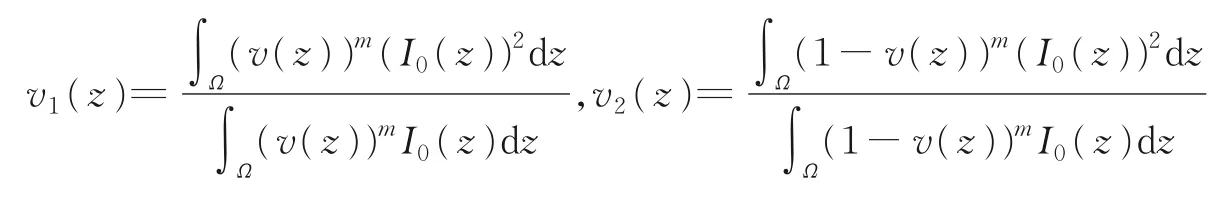
该模型虽然可以分割具有弱纹理的灰度不均匀图像，但对于复杂背景的图像分割性能并不好，只能分割目标明显的图像。

2 本文模型

2.1 模型描述

基于上述分析，本文提出了一种可用于分割具有较大噪声以及混合噪声和弱纹理的图像分割模型。理论研究表明，变异系数对于探测不同的噪声区域也更有意义。模型用模糊隶属度函数测量前景和背景图像的隶属度。首先用HLFRA提取图像的局部和空间信息，然后用变异系数法对数据项进行拟合。利用结合了像素空间信息的局部区域信息来近似给定图像中的灰度值。图像域中的像素是以像素x为中心的方形或圆形邻域内的像素。局部区域的平均灰度值定义为式（15），具体含义如图1所示。

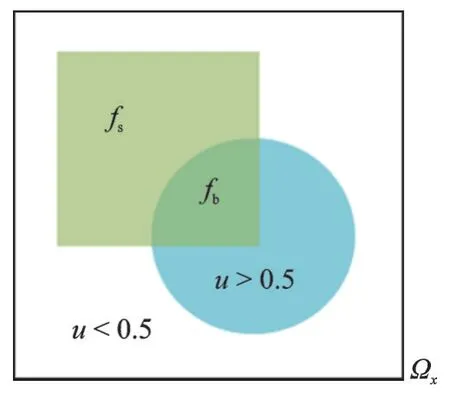
图1 fs和fb示意图Fig.1 Schematic diagram of fs and fb

式中u(y)为局部图像区域Ωx的模糊隶属度函数。

式中局部权重函数ω(x，y)用来提取图像的局部信息，定义为

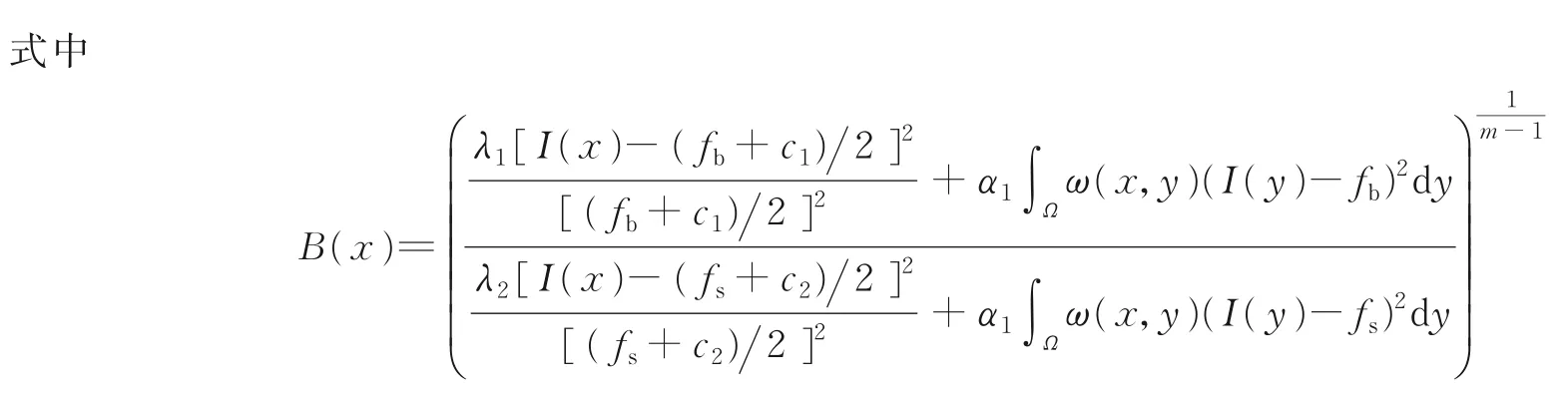
对伪水平集进行正则化，并在进化过程中保持形状平滑的外观，边缘能量是由正则项和惩罚项组成，与式（12，13）一致。

此模型利用变异系数作为局部区域统计量，在很大程度上避免了异常值和噪声对分割的干扰。区域能量可以平衡目标和背景的重要性，驱使初始轮廓向目标边界移动。边缘能量对伪水平集函数进行正则化，保持曲线演化过程中的平滑性。

2.2 数值实现

为了解决式（18）中区域能量的计算问题，目前流行的基于区域的ACM能量函数最小化是利用梯度下降法求解，但收敛速度较慢。受FEAC模型［11］的启发，直接计算新能量与旧能量的差ΔFCR=F̂CR-FCR，以此来进行伪水平集的迭代。首先将式（18）中的能量泛函从连续空间转换到离散空间。然后为了提高计算效率，直接计算新能量和旧能量的差值。如果ΔFCR为负值，则用新值替换旧值；否则，旧值保持不变。值得注意的是，当式（8）中定义的能量泛函为凸时，全局最小能量泛函很容易通过迭代的方式得到。在文献［1］中已经证明了它的凸性。

令P∈I为图像域Ω中的一个给定的点，其强度值和隶属度分别为I0和u0，旧的全局能量泛函为FCR，对于点P，新的隶属度函数为un，用替代更新后的c1、c2、fb、fs的值，且当隶属度函数变为un时，全局能量泛函用表示。能量泛函的变化形式为

式中ω(x，y)为空间加权系数。

从以上计算过程可以看出，本文可以通过计算新旧能量函数的差值来判断伪水平集是否需要更新。在计算过程中，FEAC模型［11］中的伪水平集根据曲线演化过程中逐像素能量函数的变化进行更新。与FEAC模型不同的是，本文直接计算2个能量函数的变化：更新前的旧能量泛函和更新后的新能量泛函。

在计算边缘能量的过程中，计算了式（12，13）中能量泛函的导数，得到

2.3 算法步骤

本文算法的流程如下：

3 实验结果与分析

本文共做6个实验来检验提出模型的分割性能。本文模型中有8个参数需要设置，即：λ1、λ2、α1、α2、β1、β2、最大迭代次数IterNum以及被大小为(2k+1)×(2k+1)的窗截断的局部加权系数ω(x，y)。在本文实验中将伪水平集内外的区域分别设置为0.7和0.3，默认参数设置为m=2，局部加权窗口k=3，最大迭代次数IterNum=100，β1=β2=1。目标越大，λ1越大，若要保留图像边缘和细节信息，λ2也要越大。α1、α2与λ1、λ2的作用相同，但都不宜取过大，一般不超过5。自然图像来自Segmentation Evaluation数 据 库［18］和Berkely Segmentation Dataset BSDS500［19］。实 验 环 境 采 用Matlab（R2018b），Intel（R）Core（TM）2 Quad CPU Q9500@2.83 GHz，4 GB内存，Windows 7操作系统。

3.1 多目标图像分割

实验1验证了本文模型对多目标图像分割的有效性。实验中选取5幅图像进行分割，结果如图2所示。图2中第1列为原始图像加初始轮廓，第2列为分割结果，第3列为分割结果的二值图像显示，第4列为对应的水平集函数图像。从实验结果可以很明显地看出，本文模型可以对多目标图像进行准确分割。

3.2 对比实验

实验2验证了本文模型对自然图像分割的有效性，并与FRAGL［20］和HLFRA模型进行对比，结果如图3所示。图3中第1列为初始轮廓，第2列为FRAGL模型分割结果，第3列为HLFRA模型分割结果，第4列为本文模型分割结果。图3结果表明，虽然在对具有明显轮廓的图像进行分割时，HLFRA模型和本文模型的分割结果没有太大差距，但在对纹理稍微复杂一点的图像（如仙人柱）进行分割时，本文模型有明显优势，可以准确提取其轮廓。除此之外，本文也对比了3个模型的CPU运行时间，结果如表1所示。从表1可以看出，虽然3个模型用时都比较少（用时较短的用黑体已标出），但相对于FRAGL和HLFRA模型，本文模型更快、更具有优势。

图3 不同模型对自然图像以及合成图像分割的结果Fig.3 Segmentation results for natural and synthetic images using different models

3.3 初始轮廓鲁棒性验证

实验3对初始轮廓的鲁棒性进行验证。设置不同初始轮廓的位置和大小，在合成图像和灰度不均匀图像上对其进行验证，结果如图4所示，图（a~f）中左图为初始轮廓，右图为分割结果。图4结果表明，无论初始轮廓是否包含了目标，都可以对其进行准确分割。

图4 本文模型对初始轮廓的鲁棒性Fig.4 Robustness of initial contour by the proposed model

3.4 轮廓演化过程

为了更直观地观察曲线演化过程，实验4对仙人柱的分割过程进行呈现，每经过10次迭代展示一次，结果如图5所示。当迭代50次时，就可精确分割出仙人柱的轮廓。

图5 对仙人柱进行分割时的曲线演化过程Fig.5 Curve evolution process of partitioning Cactus image

3.5 噪声鲁棒性验证

实验5使用HLFRA模型和本文模型对增加不同噪声的自然图像进行分割，结果如图6所示。为了验证本文模型的鲁棒性，在图6中加入了均值全为0和方差分别为0.05的高斯噪声（第1列），0.05的斑点噪声（第2列），0.02的椒盐噪声（第3列），方差为0.02的高斯噪声+方差为0.02的椒盐噪声（第4列），方差为0.02的高斯噪声+方差为0.02的椒盐噪声+方差为0.05斑点噪声（第5列）。图6中的分割结果表明，只有本文模型能准确地提取出5幅高噪声图像中的目标。

图6 噪声图像的分割结果Fig.6 Segmentation results of noisy images

3.6 客观评价指标

本文采用Dice相似系数DSC和Jaccard指数JSC对分割结果进行评价。Dice系数是一种集合相似性度量指标，通常用于计算2个样本的相似度，取值范围为［0，1］，分割结果越好，值越大。Jaccard指数是比较样本集的相似性和多样性的统计量，值越大说明相似度越高。2个指标定义为

式中：S1表示真实轮廓；S2表示模型分割结果。在Berkely Segmentation Dataset BSDS500数据集选取3张图像（图7），并与HLFRA模型的分割结果进行比较，其指标对比如表2所示。表2结果验证了本文模型的优越性。

图7 用于客观评价的图像Fig.7 Images for objective evaluation

表2 客观评价指标的比较Table 2 Comparison of objective evaluation indexes

4 结束语

本文基于变异系数和模糊集，提出一个针对活动轮廓图像的分割模型。该模型首先利用变异系数对结合了图像空间信息的局部灰度值进行拟合，得到区域能量泛函，驱使曲线向目标移动。然后结合边缘能量，保持演化曲线的光滑性，使其能精确地停在目标边界。最后，通过直接计算新旧能量函数之间的差异对伪水平集进行更新。实验结果表明，本文模型能够成功地从高噪声、混合噪声以及高强度不均匀性的合成图像和真实图像中提取目标，并且结果不受初始轮廓（位置和大小）的影响。