一种基于实值变分贝叶斯推断的大规模MIMO系统下行信道估计方法

戴继生，尚河坤

（江苏大学电气信息工程学院，镇江 212013）

引 言

大规模多输入多输出（Multiple input multiple output，MIMO）系统具有较高的频谱效率和能量效率，已成为下一代无线通信技术的重要组成部分［1‑2］。能否精确地获得信道状态信息（Channel state in‑formation，CSI）是制约大规模MIMO系统性能的重要因素之一。由于基站（Base station，BS）端天线数量众多，而下行信道估计的训练开销与BS端天线数量成正比，因此大规模MIMO系统的下行信道估计变得异常困难。基于时分双工（Time division duplex，TDD）的大规模MIMO系统在估计出上行信道后，可利用上/下行链路信道的互易性［1］获得下行链路信道的估计值。然而，目前主流的通信系统通常采用了频分双工（Frequency division duplex，FDD）技术，基于TDD的互易信道估计方案无法直接应用。

现有研究表明，由于无线传播环境中的散射数量有限，大规模MIMO信道的有效维数远小于BS端天线数。近年来，国内外研究人员利用大规模MIMO信道在角度域的稀疏特性，提出了大量基于稀疏表示的下行信道估计方法［3‑6］。例如：Rao等利用均匀线性阵列（Uniform linear array，ULA）流型的离散傅里叶变换（Discrete Fourier transform，DFT）具有的稀疏特性，提出了一种基于L1‑norm最小化的大规模MIMO信道估计方法［5］。随后，Wen等提出了一种基于DFT的近似消息传递大规模MIMO信道估计方法［7］。然而，大规模MIMO信道在有限维度的DFT字典矩阵上，仅存在近似稀疏表示，不可避免地存在能量泄漏的问题［8］，且基于DFT的信道估计方法仅适用于ULA。为了解决能量泄漏问题，Dai等提出了一种基于离格更新的稀疏贝叶斯学习（Sparse Bayesian learning，SBL）信道估计方法［9］，同时进一步讨论了配置任意阵列的大规模MIMO系统的信道估计方案。实验仿真结果表明，基于离格更新的SBL信道估计方法极大改善了下行信道估计性能［9］。

SBL方法在每一次迭代时，需要计算一个高维度的复矩阵逆，这将会导致较高的计算复杂度。Zhou等提出了一种基于酉矩阵变换的实值SBL方法［10］，该方法将复矩阵求逆转化为实矩阵逆，有效地降低计算复杂度。在酉矩阵变换过程中，观测矩阵的维度增加了一倍，Zhou等进一步利用信号空间和噪声空间的正交性压缩了观测矩阵的维度［10］。然而，在实际应用时，信号空间只能近似计算获得，不可避免地带来性能损失。

本文提出一种新的基于酉矩阵变换的实值SBL方法，该方法将信号空间矩阵看成一个变量，在迭代过程中自适应地调整信号空间矩阵，从而获得更好的信道估计性能。在贝叶斯推断过程中，信号空间矩阵和稀疏信号矩阵高度耦合，使得传统的SBL推断方案无法适用。为了应对该挑战，本文引入了列向量独立分解的贝叶斯变分假设［11］，从而成功地将信号空间矩阵和稀疏信号矩阵解耦。实验仿真结果验证了本文所提方法的有效性。

1 数据模型与实值SBL回顾

1.1 数据模型

大规模MIMO系统由一个具备Nt个发射天线的BS和若干个具备Nr个接收天线的移动用户（Mo‑bile user，MU）组成。由于各个MU接收的信号相互独立，仅考虑其中一个用户的信道估计问题。BS到MU的下行链路信道矩阵可以表示为［12‑13］

式中：Nc为散射簇的数量；Ns为每个散射簇的子路径数；ξc，s为在第c个散射簇中，第s个子路径的信道增益；θc，s和φc，s分别为表示相应的发射角（Angles of departure，AOD）和到达角（Angles of arrival，AOA），a(θc，s)∈CNt×1和b(φc，s)∈CNr×1分别为发射和接收阵列天线的导向矢量。MU接收到的下行链路信号Y∈CT×Nr可表示为

式中：X∈CT×Nt表示T时刻内发送的导频序列；N∈CT×Nr为零均值方差为σ2的复高斯白噪声。

1.2 实值SBL方法回顾

Zhou等提出了一种基于酉矩阵变换的实值SBL方法［10］，该方法将复矩阵求逆转化为实矩阵逆，其主要思想是在导频矩阵X中引入酉矩阵实值变换矩阵，即

式中：G∈RT×Nt为随机生成的并且服从实高斯分布；QNt表达式为

INt/2和JNt/2分别为单位阵和反对角线上全为1、其余元素全为0的矩阵。若选择ULA的几何中心作为导向矢量的参考点，a(θ)可写为

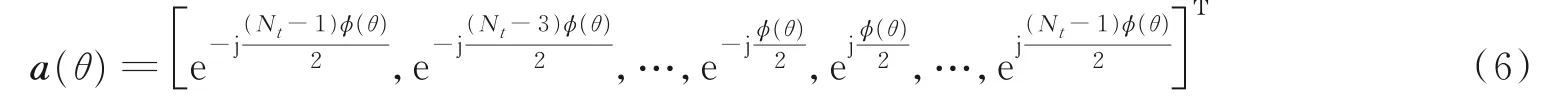
式中：ϕ(θ)=(-2πdλ)sinθ，λ为波长，d为相邻两个传感器之间的距离。若定义aˉ(θ)=QNta(θ)，则有［15‑16］

式中：Σs和Σn分别包含信号空间M个较大的奇异值和噪声空间Min{T，2Nr}-M个较小的奇异值，Us和Vs分别对应于信号空间的左和右奇异特征向量矩阵，Un和Vn分别对应于噪声空间的左和右奇异特征向量矩阵。此处，最大奇异值的η%作为阈值来确定该奇异值是否显著。等式（9）两边同时右乘Vs，可将观测矩阵的维度压缩至M，即

2 新实值SBL方法

与现有实值SBL方法不同，为了避免Vs估计不准确带来的性能损失，新实值方法将Vs看成一个变量，拟在迭代过程中自适应地调整信号空间矩阵，从而获得更好的信道估计性能。为此，在式（9）中引入一个变量矩阵V∈RM×K，即

式中K=2Nr。根据子空间理论，若V张开的空间与信号空间一致，式（9）与式（12）等价。本小节的目标是在恢复稀疏矩阵Wˉ的同时，自适应调整V，使其趋近于真实的信号空间。由于引入了变量矩阵V，信号空间矩阵和稀疏信号矩阵高度耦合，使得传统的SBL推断方案无法适用。在贝叶斯推断过程中，为了解决信号空间矩阵和稀疏信号矩阵的高度耦合问题，本文将引入列向量独立分解的贝叶斯变分假设［11］，从而使得信号空间矩阵和稀疏信号矩阵成功解耦。

2.1 SBL建模

根据传统的稀疏贝叶斯模型，有

2.2 变分贝叶斯推断

2.3 网格更新

由此，获得了一个离网模型［9］

2.4 分析与讨论

本文所提方法计算复杂度的分析如下：（1）在更新式（23）中的U和Σ时，计算复杂度分别为在更新式（26，29，32，38）中的因此，本文所提方法在每一次迭代过程中总的计算复杂度为这与文献［9，10］中的方法具有相同的计算复杂度，如表1所示。然而，值得注意的是：（1）本文所提方法涉及到的矩阵运算均为实值运算。因此，与原始的Off‑grid SBL方法相比，本文所提方法可以节省大量的计算。（2）虽然本文所提方法与文献［10］中的Real‑valued SBL方法均为实值估计方法，具有相同的计算量。但是，本文所提方法能够表现出较为优异的估计性能。

表1 计算复杂度对比Table 1 Computational complexity comparison

由于式（23，26，29）的更新规则仅与U、Σ、̂以及有关，所以只需要更新这几个参数即可。根据文献［19］提出的参数化转换方法，对应的子参数优化问题可表示为

式中上标(⋅)()i表示第i次迭代对应的值。根据文献［20］中的定理2‑b，交替优化算法生成的迭代序列收敛到优化问题（19）的一个鞍点解。

3 仿真结果与分析

将本文方法与下面4种方法进行比较：DFT方法［5，21］、Overcomplete DFT方法［8］、Off‑grid SBL方法［9］以及Real‑valued SBL方法［10］。3GPP空间信道模型（Spatial channel model，SCM）［13］将用于生成CSI，下行链路的频率为2 170 MHz。为了确保信道估计结果具有统计特性，定义信道估计的标准化均方误差（Normalized mean square error，NMSE）为

在实验1中，假设基站由配有100个阵元的ULA组成，每个MU配备了4根天线。图1中所有的结果对应于500次Monte Carlo实验的平均值，每一次实验均在-90°~90°之间随机产生2个散射簇，且每个散射簇有10个子路径。将信噪比（Signal‑to‑noise rate，SNR）固定在0 d B。除了DFT方法外，其他方法的网格点数固定取值为150或200。图1给了不同算法的NMSE随训练导频数的变化情况。根据仿真实验结果可知，所有方法的NMSE都是随着训练导频数的增大而减小，其中DFT方法的性能最差，Overcomplete DFT方法次之。由于所提方法与现有SBL方法（Off‑grid SBL方法、Real‑valued SBL方法）均采用了离网模型，所以能够表现出较为优异的性能。特别是所提方法将信号空间矩阵看成一个变量，在估计过程中自适应地调整信号空间矩阵，有效地增强了信道估计性能。

图1 不同算法的NMSE随训练导频数变化情况Fig.1 NMSE curves of different algorithms versus number of training pilots

在实验2中，除了将训练导频数固定在50，其他所有的实验条件与实验1相同。图2给了不同算法的NMSE随网格点数的变化情况。除DFT方法外，由于其余方法均采用了离网模型，所以其NMSE均随着网格点数的增大而呈现下降趋势。但从仿真结果可以看出，本文所提方法与现有SBL方法在处理方向不匹配问题上表现更为优异。总体来看，不管网格点的个数取多少，本文所提方法都会表现出比较优异的信道估计性能。

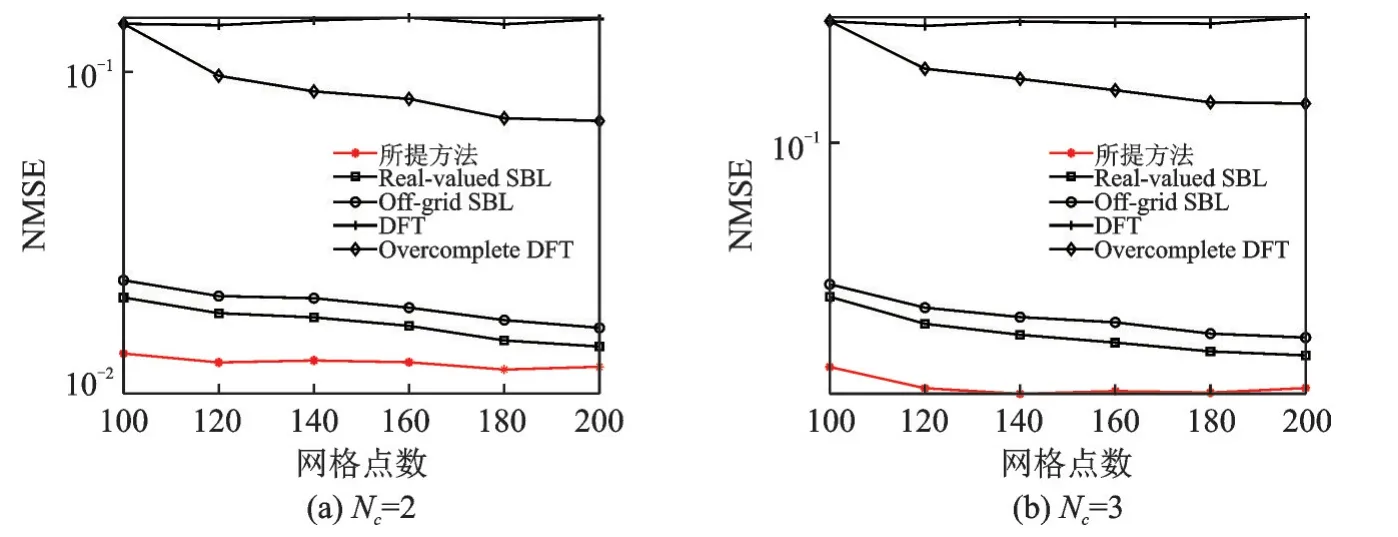
图2 不同算法的NMSE随网格点变化情况Fig.2 NMSE curves of different algorithms versus number of grid points

在实验3中，除了将训练导频数和网格点数分别固定在50和150，其他所有的实验条件保持不变。图3给了不同算法的NMSE随用户天线数的变化情况。仿真结果表明，DFT方法的性能最差，Over‑complete DFT方法次之，且这两种方法的表现性能不受用户天线数量的影响。基于SBL估计方法的NMSE均随着用户天线数量的增多而减小，Real‑valued SBL方法较好于Off‑grid SBL方法，本文所提方法估计性能显著优于其他方法。

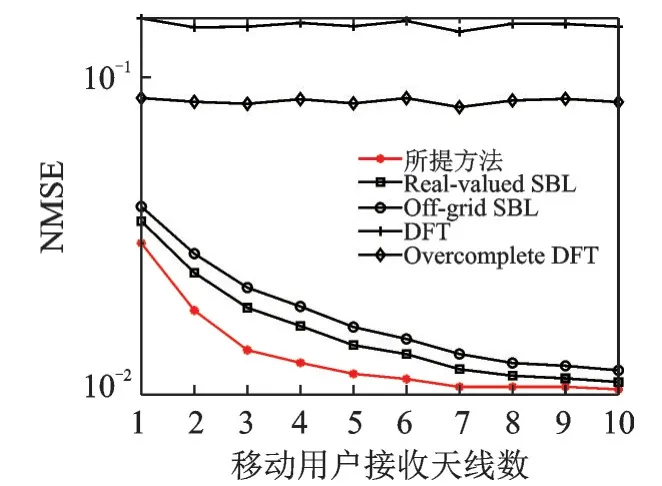
图3 不同算法的NMSE随用户天线数变化情况（Nc=2）Fig.3 NMSE curves of different algorithms versus num‑ber of user antennas with(Nc=2)

在实验4中，除了将训练导频数、网格点数和用户天线数分别固定在50、150和4，其他所有的实验条件保持不变。图4给了不同算法的NMSE随信噪比的变化情况。仿真结果表明，Real‑valued SBL方法和Off‑grid SBL方法在高信噪比时的估计性能表现优异，在低信噪比时的估计性能低于DFT方法和Overcomplete DFT方法。本文所提方法估计性能在低信噪比时显著优于其他方法，在高信噪比时与Real‑valued SBL方法和Off‑grid SBL方法的性能表现基本持平。

图4 不同算法的NMSE随信噪比变化情况（Nc=2）Fig.4 NMSE curves of different algorithms versus SNR with(Nc=2）

4 结束语

针对大规模MIMO系统下行信道估计中信号空间只能近似计算获得、不可避免地带来性能损失的问题，提出了一种具有较小计算复杂度的新实值化信道估计方法。该方法的主要思想是将信号空间矩阵看成一个变量，在估计过程中自适应地调整信号空间矩阵。为了解决信号空间矩阵和稀疏信号矩阵高度耦合的难题，进一步引入列向量独立分解的贝叶斯变分假设，成功将信号空间矩阵和稀疏信号矩阵解耦。实验结果表明，基于变分贝叶斯推断的新实值信道估计算法具有较优的性能。