乙醇偶合制备C4烯烃的优化模型

李韶伟，王宇杰，熊 浪，黄圣淇

（台州学院 a.电子与信息工程学院;b.航空工程学院，浙江 台州 318000）

0 引言

C4烯烃广泛应用于化工产品及医药的生产，乙醇是生产制备C4烯烃的原料。在乙醇偶合制备C4烯烃的过程中，C4烯烃的选择性和收率［1，2］受到了催化剂组合与温度的影响。因此，探索乙醇催化偶合制备C4的工艺条件具有非常重要的意义和价值。

本文依据2021年全国大学生数学建模竞赛（CUMCM）赛题提供的不同催化剂组合与温度下的21组实验数据［1］，建立数学模型解决如下三方面问题:

1.分析乙醇转化率和C4烯烃的选择性与反应温度之间的关系。

2.探讨不同的催化剂组合与反应温度对乙醇转化率和C4烯烃选择性的影响。

3.探讨选择合适的催化剂组合与温度，使得C4烯烃收率尽可能高。

1 温度对化学反应的影响

依据赛题所提供的21组实验数据，探讨反应温度对乙醇转化率和C4烯烃选择性的影响。实验的数据量不大，可以直观得到：在催化剂保持不变的情况下，反应温度与乙醇转化率和C4烯烃选择性存在较强的正向相关性。本文以A1这一组数据为例，给出下述模型结果。

1.1 指数回归曲线方程模型

利用化学动力学中的阿伦尼乌斯方程［3］探讨化学反应速率与温度之间的关系，其关系式为

其中X1代表温度，Ea表示反应活化能，R代表摩尔气体常数。

根据乙醇转化率的概念可知，乙醇转化率为：

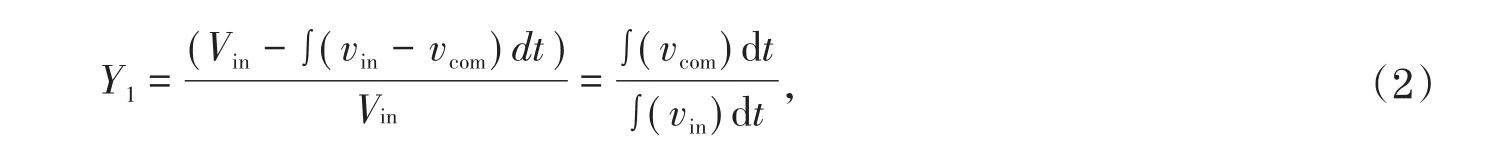
其中Y1表示乙醇转化率，vin表示乙醇进气速率，vcom表示乙醇反应速率。

在催化剂相同的情况下，乙醇进气速率vin未发生改变。从化学动力学角度分析，乙醇反应速率vcom=kp，其中k表示反应速率常数，p代表生成物性质，由化学反应平衡可以推出p为常数。因此，可以得到乙醇转化率与反应温度之间满足关系为：

将上式的常数项整合，化简后可构造出乙醇转化率-温度的拟合方程为：

将温度X1视为自变量，乙醇转化率Y1作为因变量，使用MATLAB拟合工具箱，基于最小二乘法拟合出A1实验中乙醇转化率与温度所满足的指数回归曲线方程为：

其曲线图形如图1所示。

图1 A1实验的乙醇转化率与温度所满足的指数回归曲线方程曲线图

上述回归曲线的拟合优度R2=0.9760，RMSE=2.1111，拟合效果极好，该指数回归曲线方程模型适用性好、健壮性较强。

同理可得，A1实验温度与C4烯烃选择性所满足的指数回归曲线方程为：

其曲线图形如图2所示。

图2 A1实验的C4烯烃选择性与温度所满足的指数回归曲线方程曲线图

同理可得出另外20组实验的温度与乙醇转化率以及C4烯烃选择性的指数回归曲线方程。

通过对比上述21组实验，可得A3、A7、A2、A1、A4实验结果较佳，而A11采用石英砂替代HAP，催化效果不佳，后述将不予考虑。

1.2 催化剂组合和温度对化学反应的影响

为探究催化剂组合和温度对乙醇转化率及C4烯烃的影响，使用控制变量法对温度、Co/SiO2质量、Co负载量、装料比、乙醇浓度这五个指标进行逐一分析。

首先，利用分段埃尔米特插值［4］补全了部分实验缺失的325℃或400℃的对应结果，并对数据进行了标准化处理，消除了指标间量纲和数量级差别的影响。

接着，选择灰色关联分析建立影响乙醇转换率和C4烯烃选择性的关联性模型。灰色关联分析根据因素之间发展趋势的相似或相异程度，即以“灰色关联度”作为衡量因素间关联程度的一种方法。该模型计算量小，不要求大量数据，也可以弥补数据大起大落的问题。

（1）催化剂质量的灰色关联分析

根据数据绘制了不同催化剂质量，乙醇转换率和C4烯烃选择性随着温度升高而改变的序列曲线如图3所示。

图3 温度与乙醇转化率、C4烯烃选择性关系的折线图

首先不考虑其他因素的影响，只对一个灰色关联矩阵进行分析，可以得到乙醇转换率Y1、C4烯烃选择性Y2和催化剂质量X2的两级最小差和两级最大差：

其中X3,X4,X5分别表示Co负载量、装料比和乙醇浓度。

综上，经过计算，可以得到五个指标与乙醇转换率及C4烯烃选择性的关联程度，如表1所示。

表1 各指标与乙醇转换率和C4烯烃选择性关联程度

从表1中数据中可以看出有五个因素影响乙醇转换率，影响程度依重要性排序为：催化剂质量＞反应温度＞Co负载量＞乙醇浓度＞装料比；而这五个因素对C4烯烃选择性的影响程度依重要性排序为：乙醇浓度＞反应温度＞装料比＞Co负载量＞催化剂质量。

2 C4烯烃收率的优化模型

2.1 高斯过程回归的选择和构建

基于上述五个因素对C4烯烃选择性影响的重要性的排序分析，将温度、催化剂质量、Co负载量、装料比和乙醇浓度作为输入变量，C4烯烃的收率作为输出变量，搭建关于输入-输出的回归模型。由于得到数据的波动较大，传统的多元回归模型拟合效果不理想，因此这里使用高斯过程（GPR）对温度、催化剂质量、Co负载量、装料比、乙醇浓度和C4烯烃的收率进行高斯回归分析。多元高斯分布中，各指标都服从正态分布，而多元高斯分布服从联合正态分布，该分布由均值向量和协方差矩阵定义。剔除A11石英砂催化剂载体数据，总共筛选出109组实验数据集，选择其中70%（即76组）数据作为学习样本，其他33组作为验证集，用来评估检验模型拟合效果。

由回归模型和高斯过程的定义，输出Z和f*的概率分布为：

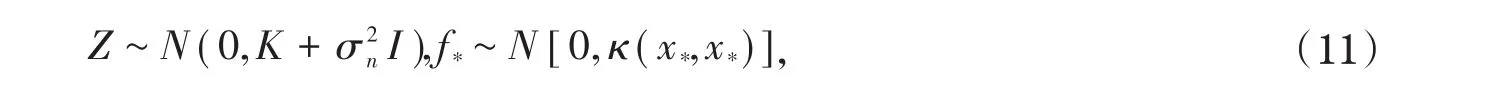
其中f*表示GPR在正态分布似然下的后验，二者的联合概率分布为：

Huang：Lao Yang，have you done the New Year’s shopping?

由联合正态分布的边缘分布性质可得

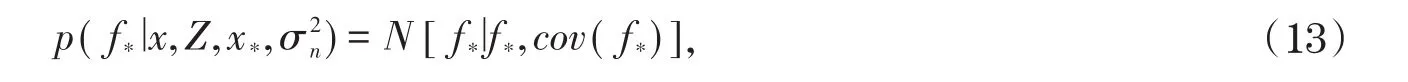
在此引入“核函数”的概念，将所生成的协方差矩阵作用在比较的两组数据集上，返回两个数据集的相似度，将它用于刻画预测值与验证集的相似度。通过MATLAB求解得到了预测值和实际值（验证集）的误差分析图（如图4所示），并进一步得到了均方差和拟合优度。

图4 预测值与验证集的误差分析图

从图4可以看出，该模型的拟合效果很好，预测数据和109组实验数据误差普遍较小。

2.2 C4烯烃收率的单目标优化模型

经过分析，乙醇转化率和C4烯烃选择性关于温度X1服从指数增长规律，而Co负载量X3在到达5wt%后会出现急剧的下降。装料比与C4烯烃收率之间会出现波峰的情况，如图5所示。因此，将装料比控制在“1”的附近，以保障较高的C4烯烃收率。乙醇浓度X5就是vin的物理意义，根据公式（3）不难看出两者存在反比的关系。

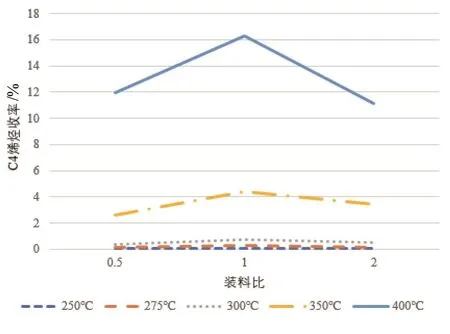
图5 装料比与C4烯烃收率的关系分析图

根据上述设定的指标限制条件，建立了如下的单目标优化模型：

其中，Z为C4烯烃收率，根据C4烯烃收率的定义，Z=Y1×Y2。

上述模型的不等式约束可由等式约束和新的边界松弛变量来替换，因此模型（14）可转化为：

其中，x为松弛变量。再进一步，模型（14）的目标函数也可以转换，即满足可行域内与原函数f(x)尽可能接近，而靠近边界时差异很大。因此模型（14）可以转化为如下的优化问题：

这里的约束条件被作为对数形式的障碍项添加到目标函数中。μ为障碍常数，μ＞0。给定一个障碍常数μ的值，如果任意一个变量x靠近边界，目标函数会立即响应并迅速增大趋于无穷。从理论上看，优化问题（16）的最优解为（14）式所定义区域的内点。障碍项的影响大小取决于障碍常数μ的值。

使用fmincon内点法求解上述优化模型，得到的迭代计算的求解过程如图6所示，模型最优解对应的变量值如表2所示。

图6 迭代计算优化模型的求解过程图

表2 模型最优解的求解结果

3 提升C4烯烃收率的实验设计

前文根据内点法求得了优化模型的最优解，得到最佳的催化剂配比和温度。然而预测值并不能保证在实际实验中的最佳效果。

将Z视为关于变量Xi(i=1,2,…,5)的函数，则变量Xi(i=1,2,…,5)∈R5围绕最优解（如表3所示）存在一邻域，使领域内点对应Z的最小值均不小于赛题附件一诸次实验［1］所得到的C4烯烃收率最大值。在该邻域内增设5次实验，以寻找实际实验的最优解。算法如下：

步骤1：计算样本数据点的误差，如图7所示。

图7 样本数据点误差图

步骤2：在变量Xi(i=1,2,…,5)的取值范围内，采用网格取点，计算各网格节点对应的Z值，选出最接近最优值的前五个预测值对应的网格节点。

步骤3：分析影响因素。对范围内的网格节点进行分析，首先通过指标数值差异分析预测值小于实际值的原因，其次分析收率被估低存不存在单一变量的影响的可能，最后分析在这个点周围是否存在异常区域的现象，即区域内大部分样本点都被估低或估高。

步骤4：调整被估低指标的参数，以期尽可能少地增设实验，达到实际实验的最优解。

最终，确定增设五组新的实验参数，如表3所示。

表3 增设实验的参数表

4 结语

本文得到现有的最优催化剂组合为200 mg 1wt%Co/SiO2-200 mgHAP-乙醇浓度0.9 ml/min，反应温度为400℃，C4烯烃最高收率为43.11%。若温度限制在350℃及以下，则C4烯烃最高收率为18.06%。而根据表2所设计的催化剂组合，理论上C4烯烃最高收率可达到50.07%。

在制备乙醇和C4烯烃过程中，本文使用了指数曲线拟合和灰色关联分析对化学反应的影响因素进行了分析。利用高斯回归模型作为机器学习方法可以有效解决回归等数据挖掘问题，对复杂数据的拟合程度较好，因此将它应用于C4烯烃收率的优化迭代。经验证，文中模型比较合理，结论可靠。