格上无陷门的无证书签名

梁红梅

（1.闽南师范大学数据科学与统计重点实验室,福建漳州363000；2.闽南师范大学数学与统计学院,福建漳州363000）

无证书公钥密码体制(Certificateless Public Key Cryptography, CL-PKC)于2003 年由Al-Riyami 和Paterson[1]在ASIACRYPT’03会议上提出.在无证书密码体制下，密钥由两部分组成.一部分由密钥生成中心（Key Generator Center，KGC）产生，另一部分由用户产生.KGC 根据用户的公开信息（如身份、邮件等）产生一个部分私钥，并将部分私钥通过安全信道传送给用户；当用户收到部分私钥后，首先验证部分私钥的有效性，然后选取一个秘密值并产生相应的公钥；用户的私钥由部分私钥和自选的秘密值组合产生.无证书公钥密码体制，能够有效地解决传统公钥密码PKI 中的证书管理问题，也能够有效避免身份基密码体制中的密钥托管问题.Al-Riyami等[1]提出了无证书密码体制之后，无证书密码体制得到了广泛的研究.无证书签名是其中一个重要研究[2-9].

随着我国商密标准算法的发展，关于无证书密码体制的商密标准算法的制定也已经起步.然而，当前关于无证书密码体制的研究大多数仍是建立在传统代数数论的困难问题上.在量子算法的分析下，它们是不能满足安全需求的.由于量子计算和量子算法给传统的密码体制带来的威胁，后量子密码逐渐成为了密码学者们研究的热点.我国也开始了后量子密码算法的征集工作.

在后量子密码当中，格密码是其中的热门研究之一[10-15].研究基于格的无证书签名方案具有一定的理论和实用价值.目前，基于格的无证书签名方案仅有田苗苗等[16]和谢佳等[17]的方案.他们的方案都是基于Lyubashevsky[18]在Eurocrypt2012 上的格上无陷门签名方案.可是，他们的方案中依然采用了陷门技术，这一点与Lyubashevsky 的工作相悖.由此，利用Lyubashevsky[19]在Asiacrypt2009 上的工作，构造了一个格上无陷门的无证书签名方案.

1 预备知识

1.1 格的基础知识

定义1（格）假设矩阵B ∈Rn×m由m个线性无关的n维向量{b1,b2,…,bm}组成，那么由B 产生的格L可定义如下：

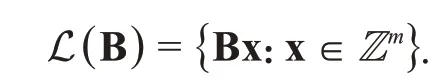
一般地，格L(B)上的最短向量记为λ1(L(B)).

定义2（SVPγ问题[20]）给定一个n维格L 和一个有理数γ ≥1，SVPγ问题的目标是在格L 上找到一个非零向量v，满足

1.2 抗碰撞Hash函数

Lyubashevsky等[21]的抗碰撞Hash函数.

设n是一个2的次幂，R是多项式环Zp[x]/xn+ 1 .

定义3（抗碰撞Hash函数族）对于D⊂R，整数是一个抗碰撞Hash函数族.其中，所有的运算都是R上的运算.

抗碰撞Hash 函数族H(R,D,m)中的任意Hash 函数h有两个性质：对于任意的ŷ,ẑ∈Rm和c͂∈R，等式͂成立.

定义4（Col(h,D)问题）给定D⊂R和函数h∈H(R,D,m)，Col(h,D)问题的目标是在Dm上找到两个不同的多项式向量成立.

根据Lyubashevsky 等[21]的工作可知，对于任意的(xn+ 1)循环格，Col(h,D)问题的困难性等价于SVPγ问题的困难性.

1.3 无证书签名方案的安全模型

无证书签名方案的安全性，可以用游戏模型来刻画.在无证书签名方案的安全模型中，一般存在两类攻击者.一类是第I 型攻击者AI，也就是非法用户，即未获得部分私钥的用户；另一类是第II 型攻击者AII，也就是恶意KGC.下面，分别用游戏Game I 和Game II 来描述无证书签名方案的安全性.游戏Game I 和Game II分别在挑战者C与第I型攻击者AI和第II型攻击者AII之间交互进行.

Game I：挑战者C首先运行系统初始化算法生成系统的主私钥msk、主公钥mpk和公共参数params，然后将系统的主公钥mpk和公共参数params发送给AI.系统的主私钥msk对AI保密.挑战者C向攻击者AI提供询问服务.

用户建立询问：攻击者AI关于身份ID进行用户建立询问，挑战者C首先为身份ID生成部分私钥、秘密值、公钥，然后将公钥返回给攻击者AI.

部分私钥提取询问：攻击者AI关于身份ID进行部分私钥提取询问，挑战者C返回相应的部分私钥给攻击者AI.

秘密值提取询问：攻击者AI关于身份ID进行秘密值提取询问，挑战者C返回相应的秘密值给攻击者AI.

公钥替换询问：攻击者AI可以关于身份ID进行公钥替换询问，挑战者C替换相应的公钥.

Hash询问：攻击者AI关于任意输入进行Hash询问，挑战者C返回相应的Hash值给攻击者AI.

签名询问：攻击者AI关于身份ID和消息μ进行签名询问，挑战者C返回相应的签名给攻击者AI.

最后，攻击者AI输出一个关于身份ID*和消息μ*的伪造无证书签名sig*.

攻击者AI赢得游戏当且仅当以下条件全部满足：1）(μ*,sig*)经验证算法验证是有效的；2）攻击者AI未关于身份ID*进行部分私钥提取询问；3）(μ*,sig*)不是签名询问返回的结果.

Game II：挑战者C首先运行系统初始化算法生成系统的主私钥msk、主公钥mpk和公共参数params，并发送给AII.挑战者C向攻击者AII提供询问服务：用户建立询问、部分私钥提取询问、秘密值提取询问、Hash询问、签名询问.（询问服务与Game I中一样.）

最后，攻击者AII输出一个关于身份ID*和消息μ*的伪造无证书签名sig*.

攻击者AII赢得游戏当且仅当以下条件全部满足：1）(μ*,sig*)经验证算法验证是有效的；2）攻击者AII未关于身份ID*进行秘密值提取询问；3）(μ*,sig*)不是签名询问返回的结果.

定义（强不可伪造性）若任意的多项式时间攻击者赢得Game I和Game II的概率是可忽略的，则称该无证书签名方案在随机谕言机模型下对适应性选择消息攻击和适应性选择身份是强存在性不可伪造的.

2 格上无陷门的无证书签名方案

本节介绍格上无陷门的无证书签名方案构造.首先简单说明一下相关参数.

由安全参数n，可定义参数m= logn，d=mn1.5logn，素数p> 4d2，且满足p= 3mod 8.当n> 4 时，可验证不等式p> 4dmn1.5logn和m>成立.根据n,m,d,p，可定义集合：R= Zp[x]/ ，D=d-n0.5logn}.

2.1 构造的方案

无陷门的无证书签名方案构造具体如下.

●Setup(n)：给定安全参数n，定义参数m，d，素数p以及相关集合：R，D，Dh，Ds，Dz.由R，D，m，定义抗碰撞Hash 函数族H(R,D,m)，并从中随机选取一个抗碰撞Hash 函数h.选取两个随机谕言机哈希函数H1,H2:{0,1}*→Dh.随机选取输出系统的主私钥̂、主公钥͂和公共参数params={n,m,d,p,R,D,Dh,Ds,Dz,H1,H2,h}.

●部分私钥提取（Extract-Partial-Private-Key）：给定系统的公共参数params、主私钥msk和用户的身份ID，操作如下：

●秘密值设置（Set-Secret-Value）：给定系统的公共参数params，用户随机选取秘密值∈，并计算

●私钥设置（Set-Private-Key）：给定系统的公共参数params、用户的部分私钥和秘密值，输出用户的私钥

●公钥设置（Set-Public-Key）：给定系统的公共参数params、用户的私钥skID和部分公钥，输出用户的公钥

●签名（CL-Sign）：给定系统的公共参数params、用户的身份ID和私钥skID，待签名消息μ，操作如下：

4)若̂∉Dmz，则重新选取̂；否则，输出签名

●验证（CL-Verify）：给定系统的公共参数params、签名人的身份ID和公钥pkID、消息签名对(μ,sig)，操作如下：

4)若3)成立，则输出“有效”；否则，输出“无效”.

2.2 正确性

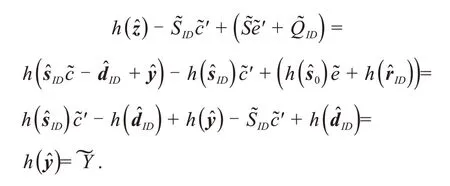
可知，签名的正确性可以有效验证.

2.3 安全性

引理1若存在第I型攻击者AI能够在概率多项式时间内以不可忽略的概率ε伪造一个我们方案的有效签名，那么挑战者C利用攻击者AI的能力获得一个Col(h,D)问题的解的概率至少是其中，e 是自然对数，tI是允许AI进行Hash询问的最大次数.

证明假设攻击者AI是一个概率多项式时间攻击者.它能够以不可忽略的概率ε伪造一个方案的有效签名.下面模拟挑战者C和攻击者AI之间的游戏Game I.

挑战者C运 行Setup(n)算法并输出主私钥、主公钥͂和公共参数params={n,m,d,p,R,D,Dh,Ds,Dz,H1,H2,h}，然后将主公钥mpk和公共参数params发送给AI.主私钥msk对AI保密.挑战者C向攻击者AI提供询问服务：

用户建立询问：挑战者C初始化列表为空.当AI关于身份IDi进行询问时，C查找列表L1.若已存在，则将返回给AI.否则，随机选取和然后将返回给AI且将保存至列表L1中.

部分私钥提取询问：当AI关于身份IDi进行询问时，C查找列表L1.若已存在，则将̂返回给AI.否则，C先自己进行一次关于IDi的用户建立询问，然后将相应的部分私钥返回给AI.

秘密值提取询问：当AI关于身份IDi进行询问时，C查找列表L1.若已存在，则将̂返回给AI.否则，C先自己进行一次关于IDi的用户建立询问，然后将相应的秘密值返回给AI.

公钥替换询问：当AI关于身份IDi进行公钥(IDi,)替换询问时，C查找列表L1中是否存在IDi.若不存在，则C先自己进行一次关于IDi的用户建立询问.最后C替换相应的公钥并将保存至列表L1中.

H1询问：C初始化列表为空.当AI关于进行H1询问时，C首先查找列表L1中是否存在若存在，则直接将相应的͂ 返回给AI.否则，C查找列表L2，如果不存在，那么随机选取∈Dh.C将相应的͂返回给AI并将保存至列表L2中.

H2询问：C初始化列表为空.当AI关于进行H2询问时，C查找列表L3.若已存在，则C直接将͂ 返回给AI.否则，C随机选取c͂i∈Dh，然后返回给AI并将保存至列表L3中.

签名询问：C初始化列表为空.当AI关于(IDi,μi)进行签名询问时，C查找列表L4.若已存在，则C直接将返回给AI.否则，C先查找列表L1以获得若列表L1中不存在IDi，则C自己进行一次关于的用户建立询问.然后，C随机选取最后，C将返回给AI，并 将分别保存至列表L3、列表L4中.

输出伪造：攻击者AI以不可忽略的概率ε输出一个关于身份ID*和消息μ*的有效伪造无证书签名其中，AI从未关于ID*进行过部分私钥提取询问，且不是签名询问返回的结果.

根据文献[23]和文献[24]的分叉引理可知，对H1函数使用分叉引理时，攻击者AI可以输出两个有效伪造签名且输出成功的概率为其中，e是自然对数，tI是允许AI进行Hash询问的最大次数.

引理2若存在第II 型攻击者AII能够在概率多项式时间内以不可忽略的概率ε伪造一个我们方案的有效签名，那么挑战者C利用攻击者AII的能力获得一个Col(h,D)问题的解的概率至少是其中，e是自然对数，tII是允许AII进行Hash询问的最大次数.

证明假设攻击者AII是一个概率多项式时间攻击者.它能够以不可忽略的概率ε伪造一个方案的有效签名.下面模拟挑战者C和攻击者AII之间的游戏Game II.

挑战者C运 行Setup(n)算法并输出主私钥、主公钥͂和公共参数params={n,m,d,p,R,D,Dh,Ds,Dz,H1,H2,h}，然后发送给AII.挑战者C向攻击者AII提供如下询问服务：用户建立询问、部分私钥提取询问、秘密值提取询问、H1询问、H2询问、签名询问.过程与引理1中的一样.

输出伪造：攻击者AII以不可忽略的概率ε输出一个关于身份ID*和消息μ*的有效伪造无证书签名其中，AII从未关于ID*进行过秘密值提取询问，且不是签名询问返回的结果.

根据文献[23]和[24]的分叉引理可知，对H2函数使用分叉引理时，攻击者AII可以输出两个有效伪造签名，且输出成功的概率为其中，e 是自然对数，tII是允许AII进行Hash 询问的最大次数.

从而，C以的概率获得了一个Col(h,D)问题的解.

根据引理1、引理2和文献[19]，可以得到定理1.

定理1在任意(xn+ 1)循环格Λ上的SVPγ(Λ)问题是难解的困难假设下，无证书签名方案在随机谕言机模型下，对适应性选择消息和适应性选择身份攻击是强存在性不可伪造的.

2.4 效率分析

已有的格上无证书签名方案中，文献[16]和文献[17]的方案较为高效.这两个方案同样都是在Lyuba‐shevsky工作的基础上构建的.Lyubashevsky工作的关键技术是拒绝采样，即无陷门.然而，文献[16]和文献[17]的方案都是在Lyubashevsky 工作的基础上加入采样技术（陷门技术）后实现无证书签名的方案.方案虽然也是在Lyubashevsky 工作的基础上构建的，但没有使用采样技术（陷门技术）.在安全强度方面，方案的安全强度是随机谕言机模型下的强存在性不可伪造.而文献[16]和文献[17]则是存在性不可伪造.如表1所示.

表1 计算复杂性和安全性比较Tab.1 Comparison of computational complexity and security

因此，方案在计算复杂度和安全强度上要优于已有方案.

3 结论

Lyubashevsky 提出了拒绝采样技术，并在此基础上构建了无陷门的签名方案.随后，在Lyubashevsky工作的基础上出现了众多具有不同性质的方案.其中便有田苗苗等和谢佳等的无证书签名方案.然而，他们在Lyubashevsky 工作的基础上又加入了采样技术和陷门技术.这与Lyubashevsky 的拒绝采样技术相悖.无证书签名方案也是在Lyubashevsky工作的基础上构建的，且没有使用采样技术或陷门技术.本方案可以被证明在随机谕言机模型下，对适应性选择消息和身份攻击是强存在性不可伪造的.