基于改进平方根变换的VSI EWMA MSE控制图
2021-12-21陈培乐王美涵杨志清
陈培乐, 王美涵, 杨志清
(闽南师范大学数学与统计学院,福建漳州363000)
广泛使用的指数加权移动平均控制图[1-2],无论是对于变量数据或属性数据,在检测过程参数的小偏移都是快速的.自适应方案[3-7]应用于EWMA 图之后,使得控制方案对工艺参数的小到中等的变化更加敏感.制定的自适应方案通过允许在工艺活动期间更新控制图的设计参数,改变抽样区间和/或样本大小和/或控制限制的宽度,从而改进控制图的统计性能.Eugenio[8]关于属性数据的自适应控制图的研究结果也表明,自适应方案能够有效提高控制图的监控性能.但是属性图通常不像变量图那样信息丰富,因为通常在数值测量中包含的信息更多,而不仅仅是用符合或不符合的术语来描述质量特征,所以考虑利用Tsai等[10]提出的改进平方根变换(ISRT)方法来改善属性数据质量特征的过程均值和方差.
Chen 等[9]提出了用于监控属性数据的可变抽样区间和样本容量的均方误差(MSE)控制图,该图在监控小偏移时的性能还有待提高.为了提高监控属性数据的MSE 控制图的监控效率,提出基于改进平方根变换的可变抽样区间的指数加权移动平均均方误差(VSI EWMA MSE)控制图,同时检测属性数据的过程均值与目标值的差异以及过程均值和标准差的偏移.还构建了该图和固定抽样区间的指数加权移动平均均方误差(FSI EWMA MSE)图的最优设计模型,并比较了两种控制方案在失控状态下的性能.
1 属性数据的VSI EWMA MSE控制图的设计
假设有一组来自二项分布的随机变量X=(x1,x2, …,xn),试验次数为k且每次试验的成功率为p,即X∼B(k,p).根据ISRT方法中二项分布转换成正态分布的反正弦变换方法,转换的式子表示为
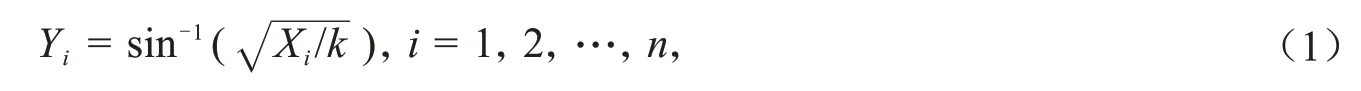
转换后的连续型随机变量Yi近似于均值为方差为1/4k的正态分布,即在Yi服从正态分布的条件下,均方误差统计量

其中T为目标值,令其中δ3为过程均值偏离目标值的幅度.令MSE*i=服从自由度为n,非中心参数为的非中心卡方分布,即MSE ∼4k(n- 1)-1.当过程受控时,过程均值没有偏离目标值,即δ3= 0,此时MSE*i的期望和方差分别为E(MSEi)=n,Var(MSEi)= 2n.
构造计数值EWMA MSE统计量Qi如下:

假设初始抽样间隔时间为t0,为了提高监控性能,给定警戒限(WL),并采用两种不同的抽样间隔时间t1和t2,其中t1 其中k为控制界限系数,w为警戒限系数. 运用马尔可夫链法计算VSI EWMA MSE 控制图的平均报警时间(ATS),其中,过程受控时的平均报警时间(记为ATS0)越大越好,过程失控时的平均报警时间(记为ATS1)越小越好,具体计算过程如下. 将受控区域[0, UCL]平均分为2m+1个小区域,每个小区域的长度为UCL/(2m+ 1),记第i个子区间为(LCLi, UCLi),i= 1, 2, …, 2m,记第i个子区间为状态i 将第i个子区间的中点记为CLi=令从状态j一步转移到状态k的概率为pjk,j=1, 2, …,2m+ 1,k= 1, 2, …,2m+ 1,则过程受控时 MSE*t服从自由度为n,非中心参数为的非中心卡方分布. 令转移概率矩阵为P=(pjk)(2m+1)×(2m+1),过程受控时的平均报警时间ATS0的计算公式为 其中,B为2m+1 维行向量,其元素除了第i个元素为1 外其余元素全为0,I为2m+1 维单位矩阵,h=(h1,h2,…,h2m+1),当区域i落在中心区域(0,WL)时,hi=t2;当区域i落在警戒区域(WL,UCL)时,hi=t1. 假设失控在过程零时刻开始发生,当过程失控时,过程均值则变为失控值0,其中δ1为过程平均值偏移幅度,过程标准差则变为失控值其中δ2为过程标准差偏移幅度. 则过程失控时 MSE*t/δ22服从自由度为n,非中心参数为n(δ1+δ3)2/δ22的非中心卡方分布. 令失控时的转移概率矩阵为P1=(p′jk)(2m+1)×(2m+1).同理,过程失控时的平均报警时间ATS1的计算公式为 VSI EWMA MSE 图的统计性能通过与FSI 图的比较来评估,使用平均报警时间(ATS)作为评价指标,ATS 指从开始检测到报警所需的平均时间.当过程处于控制之中时,最好使用一个较大的ATS0,因为较大的ATS0代表误报率越小,另一方面,当过程的参数发生变化后,ATS1越小越好. VSI EWMA MSE 图的优化模型为:给定δ1,δ2,δ3,w,t1,n的初始值,寻找使得ATS1取最小值时的最优参数组合(λ,k,t2),并且满足下列约束条件: FSI EWMA MSE图的优化模型也满足式(12)和式(13),其中t0=t1=t2= 1,w=k. 各参数的初始值分别设为:δ1取0.5,1.0,1.5,δ2取1.1,1.5,2.0,δ3取0,t1取0.1,0.5,w取0.1,0.5.FSI 方案寻找给定的初始参数下使得ATS1达到最小值时的最优参数组合(λ,k),VSI方案寻找给定的初始参数下使得ATS1达到最小值时的最优参数组合(λ,k,t1). 使用最优VSI模型计算的最优ATS1值总结在表1中.表2和表3分别列出了对应的最优抽样间隔t1和最优EWMA 参数组合(λ,k).为了便于比较,表1 和表3 还分别列出了最优FSI 方案的最优ATS1值和最优EWMA参数组合(λ,k). 表1 ATS0=370,n=5,δ3=0不同w,t2值下,最优的ATS1Tab.1 Optimal ATS1 under ATS0=370,n=5,δ3=0 different values of w and t2 表2 ATS0=370,n=5,δ3=0不同w,t2值下,最优的t1Tab.2 Optimal t1under ATS0=370,n=5,δ3=0 different values of w and t2 表3 ATS0=370,n=5,δ3=0.0不同w,t2值下,最优的(λ,k)组合Tab.3 Optimal(λ,k)combination under ATS0=370,n=5,δ3=0 different values of w and t2 首先,直接比较VSI方案和FSI方案的统计性能,从表1中的结果可知,VSI方案在所有考虑到的偏移度组合下都优于FSI方案,因为VSI方案给出的平均报警时间ATS1总是比FSI方案的短.例如考虑偏移度组合δ1=0.5,δ2=1.1,δ3=0时,FSI方案测得的ATS1=17.58,其相应的EWMA参数λ=0.172,控制界限系数k=3.062(见表3);VSI 方案中w=0.1,t2=0.1 时测得的ATS1=8.876,其相应的最优抽样间隔t1=1.646(见表2),EWMA 参数λ=0.280,控制界限系数k=3.395(见表3).从表1 可以注意到,VSI 方案中,对于一个确定的抽样间隔t2,当警戒界限系数w减少时,其相应的最优ATS1值更小;对于一个确定的警戒界限系数w值,当抽样间隔t2减少时,其相应的最优ATS1值更小,即w和k都取较小值时,可以提高VSI方案的统计性能.从表2可以注意到,对于一个确定的抽样间隔t2,当警戒界限系数w减少时,其相应的最优采样间隔t1增加;对于一个确定的警戒界限系数w值,当抽样间隔t2减少时,其相应的最优采样间隔t1增加. 给出了基于改进平方根变换的最优VSI EWMA MSE 控制图的设计方案,不同于监控属性数据的计数值控制图的自适应方案.此外,还增加了平方根变换的方案,设计了属性数据的最优VSI EWMA MSE控制图的优化模型,同时侦查过程均值和目标值的差异,以及过程均值和过程标准差的偏移.结果表明,最优VSI EWMA MSE图的统计性能优于最优FSI EWMA MSE图,能够更快地发现过程中的异常波动.
2 属性数据的VSI EWMA MSE控制图的ATS计算

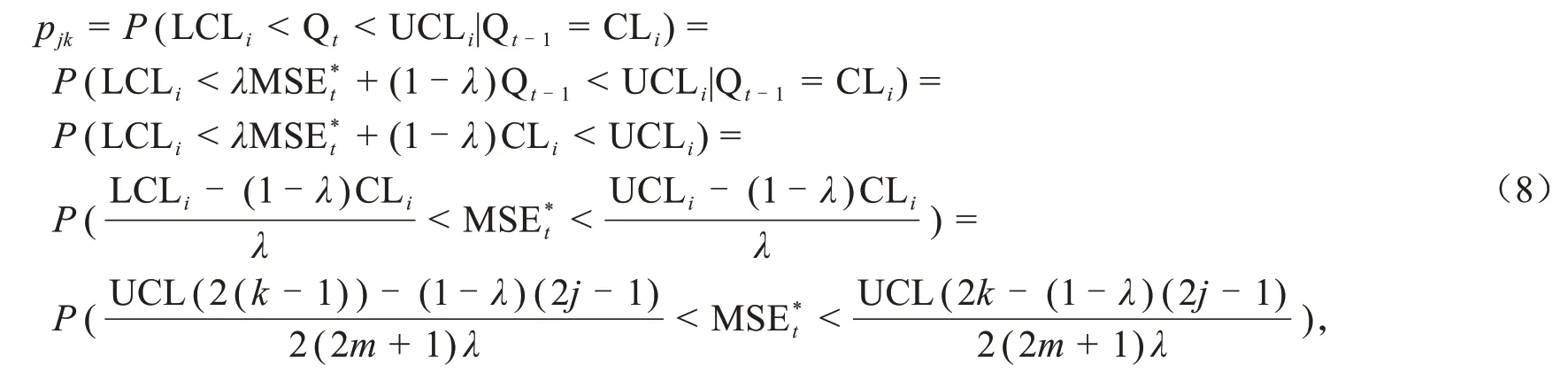



3 属性数据的VSI EWMA MSE控制图的表现




4 结论
