轻量化网络模型实现相位的快速解缠绕
2021-12-21方金生张会冉
方金生, 张会冉
(1.闽南师范大学计算机学院,福建漳州363000;2.数据科学与智能应用福建省高校重点实验室,福建 漳州363000)
相位缠绕问题存在于合成孔径雷达的图像重建、微波遥感、医学图像处理等领域,这是由于通过上述的成像系统获得的相位图像需经过相应的数学运算而产生相位缠绕问题,即所有绝对值大于π 的相位值都会被褶卷至(-π,π]之间,这与真实图像存在极大偏差.因此若要在此类图像上进一步提取有用的信息,需进行相位解缠绕,获取正确的相位值.迄今为止,国内外已有不少研究团队提出相关的算法,大致可分为传统算法和基于深度学习的算法.传统算法主要有基于路径[1]、基于区域[2]和基于拉普拉斯函数[3]的三类解缠绕算法,但这些方法都存在求解速度慢或精度较差的问题.
深度学习是近年来计算机视觉领域的研究热点,随着各类卷积神经网络模块的引入,其性能得到很大提高且已广泛应用到图像识别、图像分类、图像重建和图像分割等相关领域中[4-7].然而,深度神经网络模型性能的提升,往往是以增大网络层数和浮点运算量为代价[8-9].为此,国内外研究团队提出了多种轻量化模型设计。2016 年,Iandola 等[10]提出SqueezeNet,该网络通过使用引入更小卷积核、减少输入特征维度等方法将模型规模压缩,实现和AlexNet[4]相近的精度,且参数量仅为后者1/50.2017年,Chollet等[5]提出提出深度可分离卷积,有效地减少运算量.同年,Howard 等[6]提出MobileNets,该网络利用深度卷积和点卷积操作,从而得到可应用于移动端的轻量化网络.Zhang等提出ShuffleNet[7]网络,采用通道重排策略,这使得网络可以在保持较好的网络性能的同时有效降低网络的参数规模.之后,ShuffleNetV2[11],MobileNetV2[12],Mobile‐Netv3[13]等进一步改进紧凑型设计提高网络速度.虽然这些深度学习模型用较少的浮点运算量便可获得较优性能,但它们并未考虑图像特征映射之间的相关性和冗余性.2020年GhostNet[14]利用通道之间的冗余信息,在原有的特征图上通过一系列的简单线性操作产生特征图,这在减少参数量的同时也提高运行速度.
在相位解缠绕领域,研究人员提出了多种基于深度学习网络算法,如UNet,PhaseNet等[15-17],这些算法能够有效进行相位解缠绕且对噪声干扰具有较强的鲁棒性,但这些方法也往往以增加层数或模型复杂度为代价来提高网络性能,这不利于算法的实际应用.为此,基于轻量型网络设计思想[10-14],提出一种用于相位解缠绕的轻量化神经网络结构G-UNet(Ghost UNet),该网络结构以UNet 为骨架网络,由多个GhostBlock 构建而成.与传统拉普拉斯解缠绕算法及UNet相比,G-UNet不仅获得拥有更高的评价指标和视觉效果,且极大地减少了网络运算量,提高模型的运行速度.
1 相关工作
1.1 GhostNet网络模型
传统卷积神经网络模型的各层网络产生的特征图中,通常会包含冗余的信息,利用这些信息,可减少参数量和计算量,且不影响网络性能[14].基于此,GhostNet 在原有的特征图上通过简单的线性操作,利用较少的参数量生成更多的特征图,从而缓解了在嵌入式设备上部署卷积神经网络难的问题[14].
GhostNet与传统的神经网络相比,最大的不同之处就是特征图的生成方式.如图1(a)所示,传统的神经网络是通过常规卷积生成所有的特征图,在不同网络层间会产生特征冗余的现象.如图1(b)所示,Ghost卷积操作可分3 个步骤:首先用常规卷积生成m个特征图;然后利用m个特征图经过线性运算Φ获得更多的特征映射,每一个固有特征图经过线性运算Φ生成s-1 个特征映射,则可得m*(s-1)个特征映射图;最后,将前两步所得的特征图融合,共可得到n=m*s个特征图以此作为Ghost卷积模块的输出数据yij,可表示为:
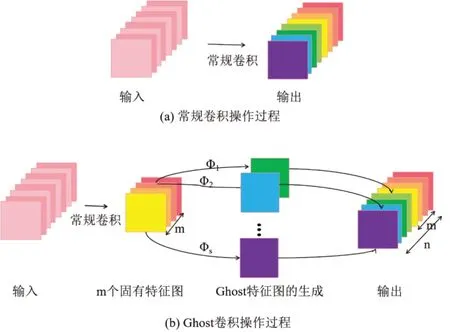
图1 常规卷积和Ghost模块运算过程Fig.1 Operation of ordinary convolution and Ghost convolution
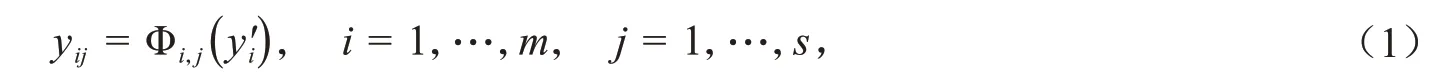
其中,y′i表示固有特征图中的第i个特征图,Φi,j表示对第i个特征图进行的第j个线性变换.
1.2 计算复杂度分析
深度神经网络中常由大量的卷积组成,这通常需要消耗较多的硬件资源和时间[18-19].在一层常规卷积中,给定输入图像X ∈Rc×h×w,经过n个卷积核运算产生n维特征图,则输出图像可为Y ∈Rn×h'×w′,其中c表示输入图像数据通道数,h和w分别代表输入图像的行数和列数,h'和w'分别代表输出图像的行数和列数.若卷积核的大小为k*k,则一层常规卷积的浮点计算量(Floating point of operations,FLOPs)为[14]:

在单一Ghost 卷积模块中,对于m个固有特征需进行m*(s-1)次线性操作,若线性操作中的卷积核大小为d*d,则一层Ghost卷积的FLOPs可以表示为:
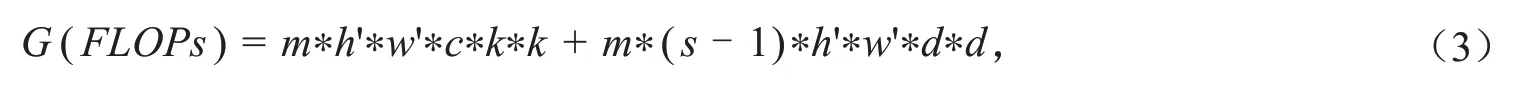
可得常规卷积和Ghost模块FLOPs比值为:
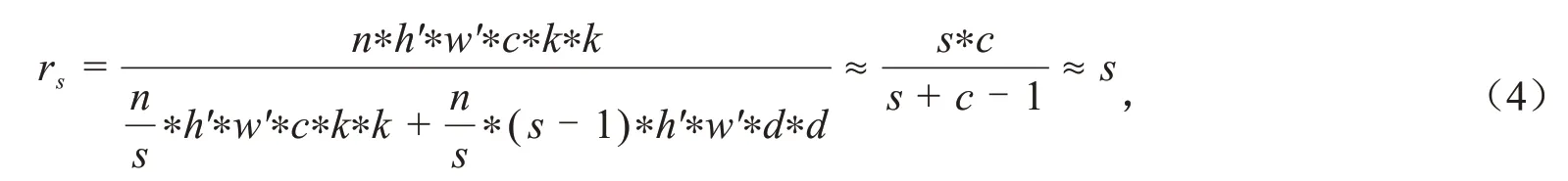
因此,部署相同层数的Ghost卷积和标准卷积神经网络,前者在计算速度上可提高近s-1倍.
2 本文方法
2.1 模型结构
2.1.1 构建GhostBlock模块
如图2 所示,设计两种GhostBlock 模块,即无残差学习的GhostBlock A 和有残差学习的GhostBlock B,其中GhostBlock A由两层的ghost卷积模块、单层批归一化(BN)处理及非线性激活函数ReLU构成;Ghost‐Block B 先用Ghost 卷积进行特征提取,再用单层的1×1 卷积降维,随后通过两个Ghost 卷积模块,1×1 卷积的输出与Ghost 卷积的输出连接构成残差块,每个层卷积后均使用批归一化进行处理[20-21].Ghost 卷积模块中一半通道用于生成特征图,另一半通道做线性变换,常规卷积中使用1×1 的卷积核,整个Ghost卷积使用3×3的卷积核.
2.1.2 基于GhostBlock的G-UNet网络
G-UNet由多个GhostBlock 构成,如图2(b)所示,主要包含两个部分:1)编码器,由两个卷积核大小为3×3 的Ghost卷积组成GhostBlock,每个GhostBlock 连接一个步长为2,卷积核大小为2 的平均池化层,对输入信息进行缩减采样的同时使得提取的特征更加平滑,在每次下采样中,将特征通道数加倍,以获得更多细节特征;2)解码器,其由上采样和短连接两部分组成,上采样过程中用步长2,卷积核大小为2的向上采样代替下采样中的平均池化层,恢复和下采样过程中一样的特征通道数,以便进行短连接,得到更加精细的特征信息,在网络的最后一层,使用1×1的卷积进行特征信息的降维输出.由于卷积神经网络的宽度会在一定程度上影响模型的性能和参数数量[22],每个卷积层的滤波器数量太少会导致性能不佳,如果数量太大,模型的训练将变的不稳定,模型的速度将大大降低.为了能够满足网络的需求,在每一层GhostBlock设置一个缩放因子α[14],用来调整G-UNet的宽度以增强网络性能.文中将由缩放因子α改变通道数后的网络结构记为G-UNetα×.
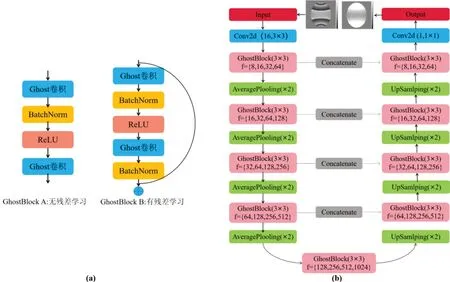
图2 GhostBlock模块与G-UNet网络结构Fig.2 GhostBlock module and network structure of G-UNet
2.2 梯度优化算法与评价指标
G-UNet 采用Adam 优化算法[23],损失函数为均方误差(MSE).采用的度量方法为峰值信噪比(PSNR)[24]和结构相似度(SSIM)[25],二者表示分别如下:
其中,Q表示图像像素灰度级,f表示真实图像,̂表示重建后的图像,μf和分别表示真实图像和重建图像的平均灰度值,和分别表示真实图像和重建图像的方差,表示真实图像和重建图像的协方差;C1和C2为稳定常数,C1=(k1L)2,C1=(k2L)2,其中,k1= 0.01,k2= 0.03.
3 实验与结果分析
3.1 数据集与实验环境
实验所采用的的数据集为仿真的磁共振相位图,创建一个128×128×60 的矩阵,于矩阵中嵌入大小不一的5个椭球分别模拟人脑以及尾状核、苍白球、鼻腔和血管,如3所示.根据组织的实际物理特性,将尾状核、苍白球、鼻腔和血管的磁化率分别设置为0.05× 10-6,0.1× 10-6,9.4 × 10-6,0.35× 10-6,除此之外,人脑的其他区域磁化率为0.根据磁化率与偶极场的物理关系式可得场图的分布情况,得到相位图根据磁共振设备的成像原理,相位图需经过四象限反正切函数求得,由于反正切函数具有周期性,其取值范围为(-π,π].随着回波时间的增加,相位值大于该范围的将被卷褶回该范围内,即产生缠绕现象,随着回波时间增加,相位缠绕的程度则愈加明显,如图3所示,同一个三维矩阵(人脑)中,不同区域的相位缠绕程度也因磁化率值的变化而不同.

图3 仿真人脑组织结构的磁化率图及不同回波时间的相位缠绕图与相应的真实相位图Fig.3 The simulated susceptibility map of brain tissue structure,the phase winding map of different echo time and the corre‐sponding real phase map
实验数据集将每一个128×128×60三维数据生成为60张128×128的二维数据作为网络的训练集和测试集,同时舍去部分无实际意义的数据,最终得到8 000 张二维数据,其中,训练集7 840 张,测试集160 张实验的标签数据均采用前向运算运算得到的真实相位图.实验的硬件环境为Intel(R) Core(TM) i7-4790 CPU, 16GB RAM, AMD Radeon(TM) R7 250.软件环境为Windows 10 的操作系统下的pycharm2019.2.3x64,网络模型采用TensorFlow+Keras框架构成.
3.2 学习率的选择
实验采用mini-batch 的训练方式,mini-batch 大小设置为16,训练所有实验达到200 轮次后停止学习.在UNet 和G-UNet 网络上将初始学习率设为10-5,以10 倍为步长增长,结果如图4 所示.对于UNet 来说,学习率为10-4,网络具有最好的收敛结果;当学习率为10-3时,由于学习步长过大,无法找到损失函数的最小值,进而无法收敛;当学习率为10-5时,网络在训练时收敛速度较慢,权重在更新时并没有达到最好的收敛情况.对于G-UNet 来说,学习率为10-3,网络的收敛情况最好;当学习率为10-2时,从图中可以发现,它的收敛情况与学习率为10-3很是接近,均在轮次为30时开始收敛,但它的前期的损失值波动较大;当学习率为10-2时,由于学习率过大,收敛时间长.因此,UNet 和G-UNet 的学习率分别为10-4和10-3.二者学习率的不同,是由于G-UNet采用Ghostblock模块,其网络层数多于UNet,同时G-UNet在特征的提取时所采用的策略与只用卷积的UNet也不同,也就是网络中的权重参数也有所区别,故造成差异.
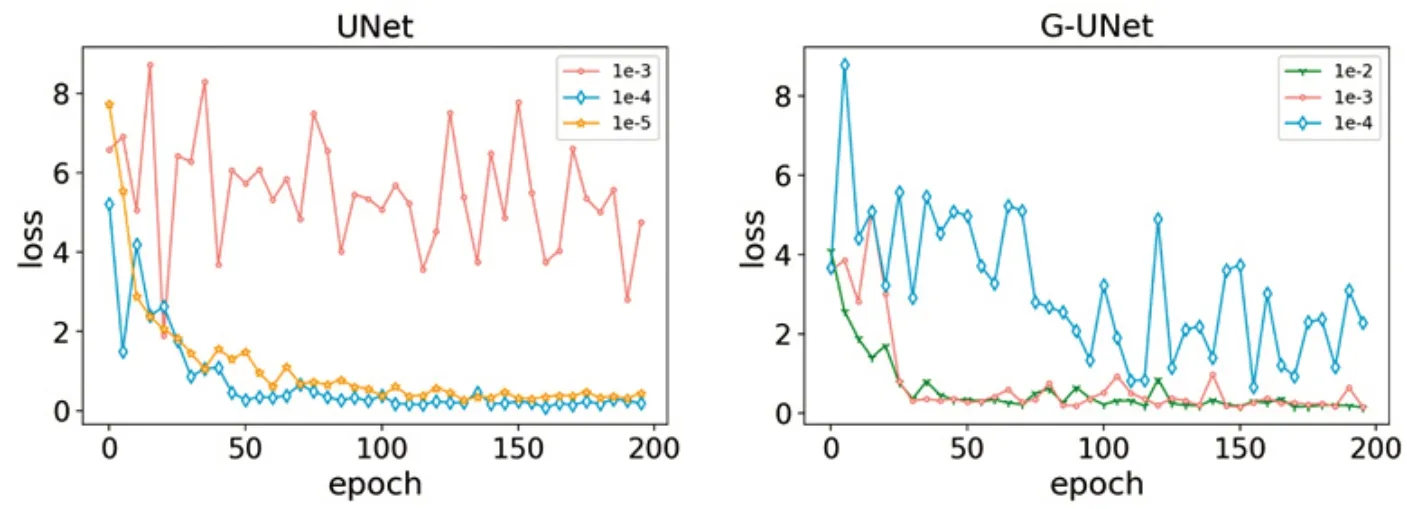
图4 两种网络学习率收敛情况Fig.4 Convergence of two network learning rates
3.3 GhostBlock残差学习对结果的影响
利用无残差GhostBlock A 和有残差模块GhostBlock B分别构建G-UNet网络,并在相位解缠绕上进行性能验证.表1 列举了分别由GhostBlock A 和GhostBlock B 构成、受缩放因子α调制的G-UNet 的浮点计算量和SSIM 值,由表1可看出由GhostBlock A 构成的网络的浮点计算量是GhostBlock B 的0.7倍,但后者具有更优的SSIM值.

表1 残差学习实验结果Tab.1 Experimental results of residual learning
3.4 相位解缠绕结果比较
G-UNet、Laplace法以及UNet算法在测试集的PSNR 及SSIM 比较结果如图5所示,G-UNet和UNet的PSNR 及SSIM 值均高于Laplace 法,同时G-UNet 和UNet 对于测试集具有相似的预测趋势.表2 中列出了三者的平均PSNR 值、SSIM 值及其参数量,由表2 可知,G-UNet 与Laplace 法相比,PSNR 提升了近1.5 dB,SSIM 提升约为0.1;与UNet 相比,PSNR 提升了0.2,在与UNet 相同的SSIM 值情况下,G-UNet 的参数量比UNet的参数量少80%.由此看来,本文方法在取得更优的相位解缠绕结果的同时大幅地减少了参数量,节省网络训练时间.
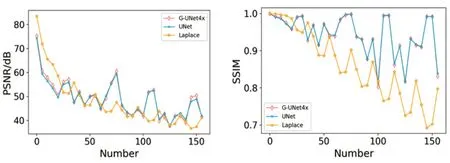
图5 不同方法每张测试集图片的PSNR和SSIMFig.5 PSNR and SSIM of each test set image by different method

表2 各个方法的平均PSNR和SSIMTab.2 Average PSNR and SSIM of each method
图6显示了三种算法在测试集上的相位解缠绕结果.图6(a)为真实相位图像(Ground truth),图6(b)~(e)为三种算法的预测结果,图6(f)~(i)为三种算法的预测结果分别与真实图像相减后的差值图.由差值图的颜色可以看出,本文提出的G-UNet 算法结果具有更多的像素点接近于0 值,即预测结果更接近于真实图像,性能优于其他两种比较算法.
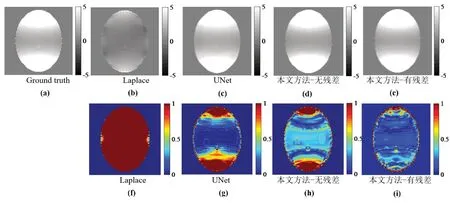
图6 不同方法相位解缠绕结果图浮点计算量与性能比较Fig.6 Comparison of floating point computation and performance of different phase unwrapping methods
图7 显示了几种算法的SSIM 与FLOPs 关系.当缩放因子较小时,G-UNet 的FLOPs 远小于UNet,但SSIM 值也略低于UNet;随着缩放因子的增加,G-UNet 的SSIM 值逐渐提高,直至缩放因子为4 时,G-UNet达到和UNet相似的SSIM值,而FLOPs仅为UNet的1/6.
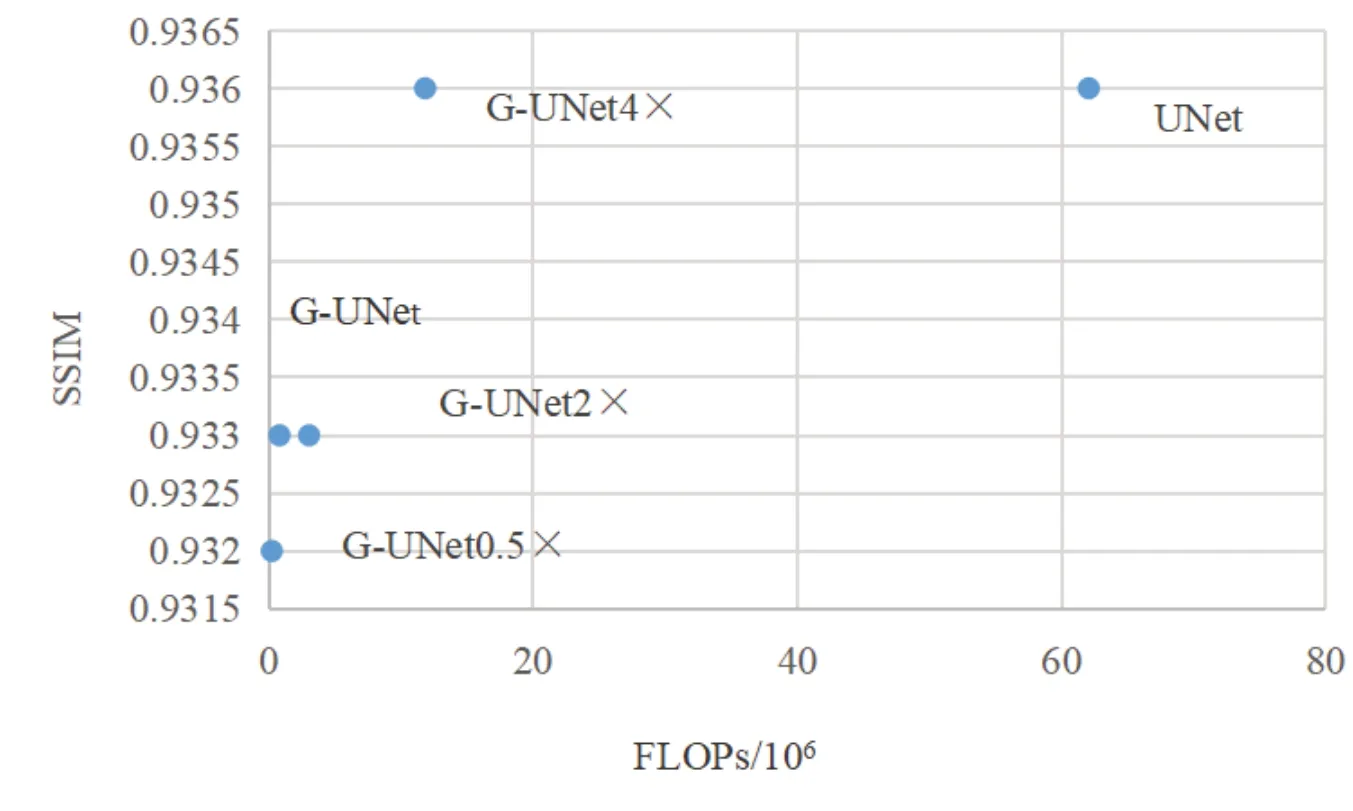
图7 不同模型FLOPs和SSIM值的比较Fig.7 Comparison of FLOPs and SSIM values in different models
综上所述,提出的G-UNet网络性能不仅优于当前主流Laplace 算法和UNet,且较UNet具有较少的参数量,对于相位解缠绕领域具有重要意义.
4 结语
提出了一种用于相位解缠绕的轻量化网络模型.实验结果表明,该模型在相位解缠绕中取得了与UNet相近的PSNR、SSIM 值,且大幅度减少了参数数量及浮点计算量,可实现快速相位解缠绕.当然,存在不足之处,所有的实验均只用于数值仿真,未进行真实人脑数据实验以及其它领域的相位解缠绕运算.
