探究团簇Fe4P的催化活性
2021-12-21侯欠欠方志刚吕孟娜井润田
侯欠欠,方志刚,秦 渝,许 友,吕孟娜,井润田
(辽宁科技大学化学工程学院,辽宁 鞍山 114051)
氢气被认为是缓解国家化石燃料日益枯竭现象最理想的选择[1],电化学裂解制氢气[2-3]因其成本低且环保而被广泛关注,该方法的高效性在于催化剂的选择. 研究学者发现铂基催化剂[4-5]对析氢反应具有高反应速率,且其具有低电位输入、高电流输出等优点,但其资源稀缺、稳定性差且成本昂贵,阻止了该催化剂大规模的应用. 目前,开发替代铂基的催化剂无疑是科研工作者研究的重中之重. 为了降低析氢反应(HER)电催化剂的成本,开发自然界中含量丰富的材料,如Fe、Co、Ni等. 其中,过渡金属磷化物(TMPS),特别是Fe-P[6-8]非晶态化合物,已经作为电化学HER催化剂得到了广泛的研究. 此外Fe-P非晶态合金因长程无序、短程有序的空间结构以及处于亚稳定状态还被用作析氧[9]、氧化还原[10-12]等反应的催化剂. 但目前研究人员都是从宏观角度分析Fe-P非晶态合金的催化性质,对其微观理论研究甚少,例如作为催化剂,Fe-P非晶态合金的哪些基本性质可以解释其具有较好的催化活性等等. 因此为解决该方面的问题,本文以团簇Fe4P[13]作为探究Fe-P体系的研究对象,根据密度泛函理论[14-17],从量子力学微观角度探究其催化性质,为其他科研人员研发Fe-P体系催化剂提供一定的理论依据.
1 团簇Fe4P优化构型的计算方法
1.1 理论模型及计算方法
依据拓扑学原理[18-20],对团簇Fe4P的初始构型设计为具有典型结构特点的4种类型,分别为平面型、四棱锥型、三角双锥型、带帽三角锥型. 在考虑自旋多重度以及Fe原子之间作用力的影响下,通过变换Fe、P原子的位置并连接Fe-Fe、Fe-P原子为共价键,从而得到16种初始构型. 将已设计出的团簇Fe4P初始构型于启天M4390微机上的Gaussian09程序中采用B3LYP泛函以及程序内置的Lanl2dz基组(即B3LYP/Lanl2dz方法)分别处于二重态与四重态下进行频率优化和全参数验证. 根据优化后的坐标在Chem3D程序中排除同一重态下且结构相同的优化构型,然后对余下的构型进行筛选,排除其不稳定的虚频构型,共得到8种优化构型. 此外,在优化过程中对各构型中Fe原子使用含相对论校正的有效核电势价电子从头计算基组进行计算,即18-eECP的双ξ基组[21-22],而对P原子采用Dunning/Huzinaga双ξ基组并加极化函数ξP.d=0.55[23].
1.2 团簇Fe4P的优化结构和能量
团簇Fe4P有二重态3种,分别为三角双锥构型1(2)、2(2)和四棱锥构型3(2);四重态5种,分别是四棱锥构型1(4)、3(4),三角双锥构型2(4),戴帽三角锥构型4(4),平面五边形构型5(4),共8种优化构型,如图1所示. 构型1(2)的能量最低,因此以1(2)为参考点(0 kJ/mol),计算出其余7种优化构型的相对能量,并在图1标出. 观察图1易发现二重态优化构型的能量均小于四重态,说明四重态各优化构型的稳定性较差,且构型5(4)的稳定性最差.
1.3 各优化构型在整个团簇中所占比例
各优化构型在整个团簇中所占的份额越大,说明该构型相比较于其他构型更能稳定存在. 因此以具有最高校正能的构型作5(4)为参考构型,将某构型的校正能相比较于参考构型减少的能量以0.001 a.u.作为一个能量单位,其单位能量的个数表示某构型的数目,该构型的个数与总的个数之比即为该构型所占比例,因此采用同样方法可以得到各优化构型所占比例,计算结果如图2所示. 由图2可以看出,团簇Fe4P各优化构型所占比例与构型能量成反比关系,即构型能量越高,其所占比例越小. 值得一提的是,构型1(2)的能量最低,在团簇Fe4P中其所占比例最高,说明在所有构型中此构型最可能稳定存在且数目最多.

图2 8种优化构型在整个团簇中所占百分比Fig.2 Percentage of eight optimized configurations in the whole cluster
1.4 团簇Fe4P各构型的热力学稳定性
由表1数据进行对比可以看出,二重态构型中构型1(2)的EZPE最低(-500.218 a.u.),EBE最大(0.502 a.u.),ΔG的绝对值最大(0.456 a.u.),由此可推断出1(2)的热力学稳定性最好.

表1 团簇Fe4P的8种优化构型的能量参数Table 1 Energy parameters of eight optimized configurations of cluster Fe4P
在图3中可以明显的发现,四重态各构型的能量均高于均值而二重态各构型的能量则与之相反,由此可以说明二重态构型比四重态构型更能稳定存在. 综上,构型5(4)~1(2)的热力学稳定性逐渐增强,其中构型1(2)的结合能和吉布斯自由能变的绝对值最大,热力学稳定性最好;而构型5(4)的结合能最小,吉布斯自由能变最大,因此其热力学稳定性最差.

图3 团簇Fe4P的8种优化构型的校正能Fig.3 Correction energy of eight optimized configurations of cluster Fe4P
综上,团簇Fe4P的各优化构型主要以二重态的形式存在,其中构型1(2)所占比例最高;构型5(4)~1(2)的热力学稳定性逐渐增强,其中构型1(2)的结合能和吉布斯自由能变的绝对值最大,热力学稳定性最好,而构型5(4)的结合能最小,吉布斯自由能变最大,因此其热力学稳定性最差.
2 团簇Fe4P的催化活性
2.1 团簇Fe4P的催化能力
前线轨道中最高占据轨道HOMO的能量(EHOMO)与最低未占轨道LUMO的能量(ELUMO)的差值即能隙差(EGAP),其数值的大小可体现出物质参与反应的活性. 能隙差越小,说明HOMO轨道的能量与LUMO轨道的能量越接近,则电子在HOMO轨道与LUMO轨道之间越容易发生迁移,即表明物质参与反应的活性越强. 表2列出团簇Fe4P的8种优化构型的前线轨道能级EHOMO、ELUMO、能隙差(EGAP)以及费米能级(EFermi)的具体数值,并依据表2绘制图4,以便更直观地反映出不同优化构型能隙差的变化趋势,从而更好地判断出8种优化构型反应活性的强弱.
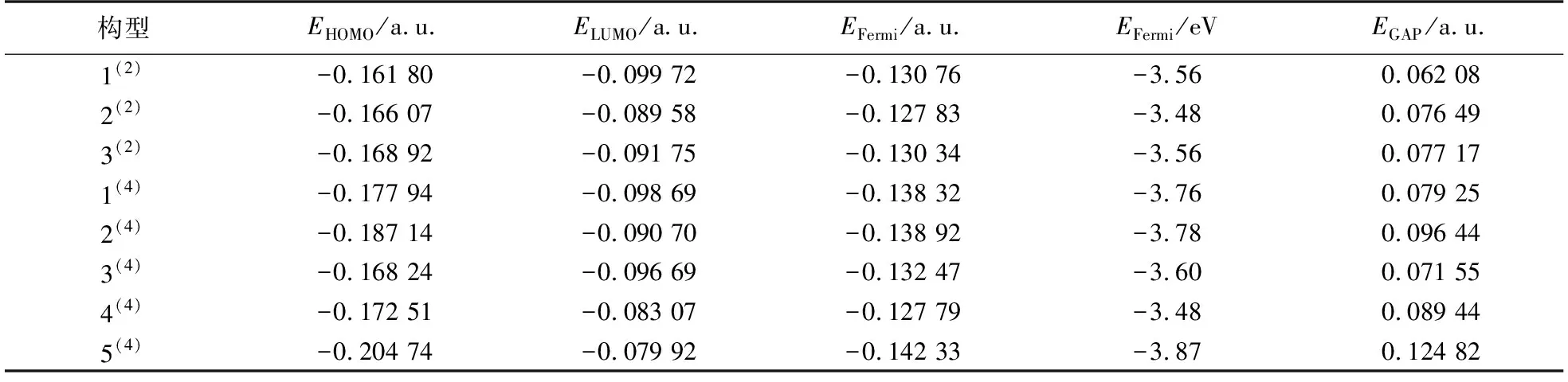
表2 团簇Fe4P的8种优化构型的能量参数Table 2 Energy parameters of Fe4P 8 optimized configurations

图4 团簇Fe4P的8种优化构型的能隙差Fig.4 Energy gap difference of 8 optimized configurations of Fe4P
观察图4可以发现构型1(2)的能隙差最小,构型3(4)次之,说明两者催化能力较强,可用于催化析氢反应的催化剂,而构型5(4)的能隙差最大,则表明此构型在参与反应时电子在轨道间的跃迁能力较弱,故反应活性较差. 此外,二重态3种优化构型的能隙差均小于四重态各优化构型(除构型3(4)外)的能隙差,说明相比较于四重态而言,二重态各优化构型参与化学反应的催化能力更强.
费米能级(EFermi)为轨道能级EHOMO与ELUMO之和的平均值,其附近的电子云密度越大,说明团簇参与反应的催化能力越强. 态密度(Density of state,DOS)表示单位能量范围内电子出现的概率密度,因此由态密度图可表征EFermi附近电子云密度的分布情况,如图5所示. 此外,费米能级左侧表示能级轨道有较多电子存在,在参与催化反应时起提供电子的作用,而费米能级右侧表示能级因具有空轨道可接受电子. 同时,费米能级两侧的最高峰距费米能级的距离也可反映出物质的催化活性,如表3所示,其中ΔPleft、EF,left分别表示左侧最高峰到费米能级(EFermi)的距离及左侧最高峰的峰值,ΔPleft越小,物质失去电子的能力越强,EF,left越高,说明左侧可参与反应的电子越多;ΔPright、EF,right分别表示右侧最高峰到费米能级(EFermi)的距离及右侧最高峰的峰值,ΔPright越短,EF,right越高,则表明物质因空轨道较多而更容易得到电子,在参与化学反应时具有较高的反应活性.

图5 团簇Fe4P的8种优化构型的总态密度图Fig.5 Total density of states of 8 optimized configurations of Fe4P
观察图5,发现除构型5(4)外,其他优化构型的态密度图最高峰均处于费米能级的右侧,并且7种优化构型最高峰的能级均为正值;除构型1(4)左侧峰距大于右侧峰距外,其余优化构型的右侧峰距均大于左侧峰距,说明团簇Fe4P在催化反应中同时具有较强的得失电子的能力. 对于二重态各优化构型,其态密度面积相差较小,右侧峰值所对应的数值也接近,由此说明二重态各优化构型具有相似的催化活性. 对表3的数据进行对比分析,发现除构型4(4)外,二重态各优化构型右侧最高峰峰值均大于四重态其他优化构型的峰值,且其右侧峰距均小于四重态5种优化构型的峰距,说明二重态3种优化构型的催化活性较强. 对于构型4(4),相比较于其他优化构型,其左右两侧面积均较小,说明构型4(4)得失电子的能力相对较弱,即催化能力最差. 此外,构型4(4)左侧峰距及左侧最高峰峰值均小于右侧(ΔPleft=2.977、EF,left=0.796 eV、ΔPright=19.609、EF,right=1.074 eV),说明其失去电子的能力强于接受电子的能力. 此处结论与上述论述的结论不相符合,由此说明仅仅从能隙差及态密度图分析团簇Fe4P的催化性质具有一定的局限性.

表3 团簇Fe4P的总态密度图最高峰及其距Fermi能级的距离Table 3 The highest peak of the total density of states of cluster Fe4P and its distance from Fermi level
综上所述,团簇Fe4P在催化反应中同时具有较强的得失电子的能力;二重态各优化构型的催化能力相似,且比四重态各优化构型的催化活性高;在整个团簇中,构型4(4)的催化能力最差,且其失去电子的能力强于接受电子.
2.2 前线轨道的研究
优化构型在参与化学反应时,其最高分子占据轨道HOMO表现出较强的给电子能力,而最低分子未占轨道LUMO则表现出较强的接受电子能力. 因此通过分析不同优化构型HOMO、LUMO图,也可判断出团簇Fe4P参与化学反应的活性,如图6所示. 图中阴影部分代表电子在此处出现的概率较大,且其覆盖面积是构型参与反应时最活跃的部分,其中红色代表分子轨道波函数的负相位,绿色代表正相位. 由图4可知,不同构型的HOMO、LUMO图各不相同,说明不同优化构型在参与化学反应时其HOMO轨道提供电子和LUMO轨道接受电子的能力均有所差异. 除构型5(4)外,其他构型的LUMO图面积均稍大于HOMO,说明团簇Fe4P在参与催化反应时得电子能力较强. 构型5(4)的HOMO图与LUMO图面积差异较小且相比较于其他构型最小,说明其在参与反应时提供电子的能力和接受电子的能力相当,且其催化能力最差. 构型1(2)、3(4)的HOMO、LUMO图几乎呈对称分布,前线轨道越对称,则HOMO轨道上的电子越容易流向LUMO轨道,即表明二者均具有较强的反应活性及催化能力.

图6 团簇Fe4P的8种优化构型的HOMO、LUMO图Fig.6 HOMO and LUMO diagrams of 8 optimized configurations of Fe4P
2.3 库普曼斯定理
电离势[24](EI)和电子亲和能[25](Eea)均表示分子中的原子成为离子所需要的能量,EI表示中性原子成为阳离子吸收的能量,Eea表示其成为阴离子所释放的能量. 电子亲和能越大,说明原子越容易得到电子成为阴离子,构型的催化活性越高,而电离势则与之相反,其数值越小,表明该构型的反应活性越强. 电负性[26](χ)的大小表征为分子中的原子参与成键时吸引电子的能力,其数值越大,说明原子越容易得到电子而带负电,从而使构型具有较强的反应活性. 亲电指数(ω)为分子接受电子的能力,与电负性具有相同的作用效果,其数值越大,越容易参与化学反应. 依据库普曼斯定理[27]并结合前线轨道能级EHOMO、ELUMO,根据相关计算式:EI=-EHOMO、Eea=-ELUMO、χ=1/2(EI+Eea)、ω=(-χ)2/(EI-Eea),计算出不同参数的相关数据列于表4. 为更直观地分析各种参数的变化趋势,依据表4具体数值绘制如图7所示的曲线图.

表4 团簇Fe4P的8种优化构型的反应活性参数Table 4 Reaction activity parameters of 8 optimized configurations of Fe4P kJ/mol

图7 团簇Fe4P的8种优化构型的电离势(EI)、亲电指数(ω)、 电负性(χ)、电子亲和能(Eea)Fig.7 Ionization energy(EI),electrophilic index(ω),electronegativity(χ) and electron affinity energy(Eea)of 8 optimized configurations of Fe4P
观察图7易发现,各优化构型的亲电指数变化幅度最大,而电子亲和能的曲线变化幅度较为平缓,其中构型1(2)的亲电指数和电子亲和能最大,构型1(4)、3(4)次之说明三者均具有较强的反应活性,而构型5(4)的亲电指数和电子亲和能最小,说明此构型在参与反应时接受电子的能力最差;相比较于其他构型,构型1(4)、2(4)、3(4)、5(4)的电负性较大,说明四重态各优化构型较二重态优化构型吸引电子的能力较强;分析与其他3个参数作用效果相反的电离势曲线,发现构型1(2)、2(2)、3(2)、3(4)的电离势较小,说明它们易失去电子成为阳离子,具有较优的反应活性. 从整体来看,构型1(2)、3(4)的反应活性较强,具有较优的催化性质,而构型5(4)的催化活性最差.
3 结论
(1)综合能隙差和态密度图来看,构型1(2)的能隙差最小,构型3(4)次之,两者参与化学反应的活性较强,而构型5(4)的能隙差最大,则此构型在参与反应时电子在轨道间的跃迁能力较弱;团簇Fe4P在催化反应中同时具有较强的得失电子的能力;二重态各优化构型的催化能力相似,且比四重态各优化构型的催化活性高;在所有构型中,构型4(4)最为特殊,具有较强的失电子能力,但其接受电子的能力也不容忽视.
(2)分析前线轨道HOMO、LUMO图,发现团簇Fe4P在参与催化反应时得电子能力较强;构型1(2)、3(4)的HOMO、LUMO图几乎呈对称分布,表明二者均具有较强的反应活性及催化能力;构型5(4)在参与反应时提供电子的能力和接受电子的能力相当,且其催化能力最差.
(3)依据库普曼斯定理,对比分析发现构型1(2)、3(4)的的亲电指数和电子亲和能较大、电离势较小,即二者反应活性较强,具有较优的催化性质,而构型5(4)的催化活性最差.
综上,从微观角度探究出构型1(2)具有最优催化活性,构型3(4)次之,构型5(4)的催化活性最差. 而在催化析氢反应中团簇Fe4P参与到吸附氢和脱氢两步反应中,但实际上团簇Fe4P起催化剂的作用. 因此通过探究各优化构型的催化活性进而选择具有最优催化活性的构型,可以为研究团簇Fe4P的催化析氢性能奠定基础,同时也为其他研究学者探究用于析氢反应的Fe-P催化剂提供一定的理论依据.
