一种可重构并联机构的拓扑特性分析

徐 帅,尤晶晶,2,沈惠平,叶鹏达

(1.南京林业大学机械电子工程学院,江苏 南京 210037) (2.江苏省精密与微细制造技术重点实验室,江苏 南京 210016) (3.常州大学现代机构学研究中心,江苏 常州 213016)

由于传统的并联机器人机构具有不变的拓扑结构和固定的运动副,这限制了并联机构的通用性与适应性. 鉴于此,2006年,戴建生教授提出了可重构机构[1],并于2009年召开全球首届 IEEE国际可重构机构与可重构机器人大会,开创了可重构机构新领域. 相比较传统的并联机器人,可重构并联机器人在保留传统并联机构优点的同时又具有多构态变化,满足多任务、多工况与多功能的要求,达到“一机多用”、节约资源与降低能耗等特点,已广泛应用在火星探测车[2]、卫星天线和太阳能帆板[3]等领域,吸引了国内外学者的广泛关注.

一些机构所具有的新型运动模式相继被发现,具有多种运动模式的并联机构综合仍然是机构学研究的热点之一. 有研究发现[4],机构拓扑演变以及活动度可变是可重构机器人的两个基本特征,几何约束是变胞机构变胞的起因. KONG等[5]综合了一类具有3自由度纯平移和3自由度纯转动的多运动模式的并联机构. GALLETTI等[6]通过利用特殊的运动副排列,综合了单环和多环运动转向机构,提出了4个基本的运动转向单环机构,并构造了具有分岔运动的并联机构. 畅博彦等[7]提出一种仅含转动副的二维移动放缩单元,通过模块化组合将构造得到的一种平面二维移动放缩机构作为支链,设计了一种新型3T1R并联机构. REFAAT等[8]基于李群理论提出了一类在分岔点实现两种运动模式的新机构. 以上设计可重构并联机构的基本思路是一致的,都以拓扑综合为主,但还没有同时考虑多工况环境功能的需求和可重构机构本身构型与活动度变化的综合设计方法.

目前,国内外有关并联机构拓扑结构设计的主要方法有:位移子群分析法[9]、方位特征集分析法[10]与螺旋理论分析法[11]. 相比较其他两种方法,基于方位特征集理论与方法,是一种描述机构运动副轴线的线矢簇的几何方法,与基坐标无关,也与运动位置无关;具有运算简单、易操作且物理意义明确,适用于低耦合度的并联机构拓扑结构设计.

本文首先设计了一种可转换主、从运动以及锁合模式的移动副;接着,通过锁合1个移动副,得到了 9种新构型,并运用基于方位特征(POC)和有序单开链(SOC)的并联机构拓扑结构设计理论与方法,详细推导了机构的POC集、自由度、耦合度这3个主要拓扑特性指标,揭示了机构的本质属性;最后,给出了锁合2个、3个、4个、5个和6个移动副后得到的重构构型的拓扑指标值,这些指标反映了可重构机构的运动学及动力学的基本性能,为后续的构型综合及运动控制提供了理论基础,进一步为可重构并联机构的推广提供了应用参考.

1 机构描述

所设计的9-3(前、后数字分别代表静、动平台上的球铰链个数)并联机构,由三棱锥状的动平台O、静平台1以及9条具有相同拓扑结构的B-P-b(B为一般球副,P为移动副,b为三重复合球铰副)支链组成[12]. 其中,每三条支链为一组,组合成一个三棱锥. 初始状态下,每组支链上的三条支链两两垂直. 其结构简图与结构模型图分别如图1、图2所示.

图1 9-3并联机构的结构简图Fig.1 Schematic diagram of 9-3 parallel mechanism

1.静平台;2.副板;3.三重复合球铰副;4.联轴器;5.动平台;6.底座;7.移动副;8.一般球副图2 9-3并联机构的结构模型Fig.2 Structural model of 9-3 parallel mechanism

首先,为了便于可重构并联机构的构型转换,设计了一种可转换主、从运动以及锁合模式的移动副,该支链的具体结构主要包括导杆、内套筒、外套筒和转换套筒,其结构模型如图3所示.

该移动副有3种工作模式:当转换套筒与导杆通过螺栓和螺母固定时,旋转外套筒,带动转换套筒和导杆一起移动,此时为驱动模式,该工作模式下的移动副又称为驱动副;当转换套筒与导杆无固定时,外套筒不起作用,导杆在内套筒的筒体内光滑移动,此时为从动模式,该工作模式下的移动副又称为从动副;当转换套筒与导杆通过螺栓和螺母固定时,外套筒固结于内套筒外表面,由于螺纹的自锁,套筒和导杆静止不动,此时为锁合模式,在该工作模式下移动副等效为刚性杆件.

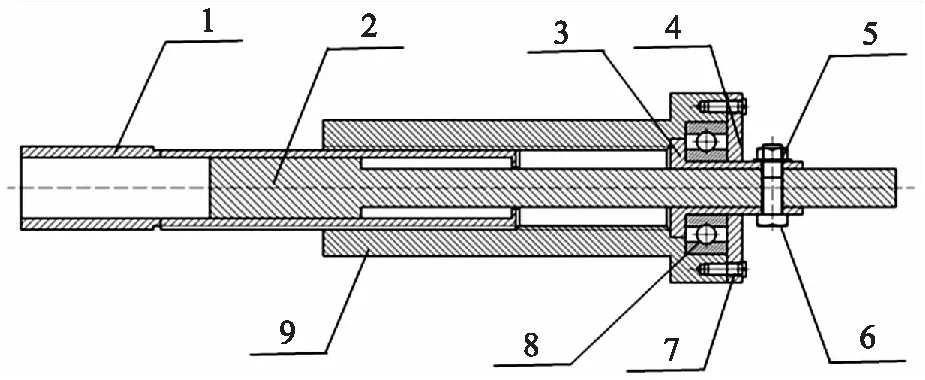
1.内套筒;2.导杆;3.挡环;4.转换套筒;5.螺母;6.螺栓;7.螺钉;8.深沟球轴承;9.外套筒图3 移动副结构示意图Fig.3 Schematic diagram of moving pair structure

2 拓扑分析

2.1 机构的POC计算

如图4所示,该机构中含5B-3P空间七杆回路的复杂支路. 该支路由3个SOC{-B-P-B-}支链在b副中心重合组成,输出构件在此处又以复合球铰副连接而成,该支链可记作为HSOC{-P(5B-3P)-P(5B-3P)-P(5B-3P)-B-}. 其中,利用移动副的不同工作模式,将机构中的P1副设置为锁合模式,将P2、P3、P4、P6以及P95个移动副设置为驱动模式.

图4 锁合机构结构简图Fig.4 Structure diagram of reconfigurable mechanism

由于并联机构动平台的POC集与支链末端构件的POC集相同,则可通过使用等效拓扑结构,求解机构的自由度,其等效形式如图5所示.

图5 可重构机构的等效拓扑结构简图Fig.5 Equivalent topology diagram of reconfigurable mechanism

(a)支链的拓扑结构如下:

混合支链Ⅰ的拓扑结构等效表示为 HSOC1{-P(5B-2P)-P(5B-2P)-B1-},混合支链Ⅱ、Ⅲ的拓扑分别为 HSOC2{-P(5B-3P)-P(5B-3P)-P(5B-3P)-B2-}、HSOC3{-P(5B-3P)-P(5B-3P)-P(5B-3P)-B3-}.

(b)选定动平台上的中点为基点O.

(c)确定支链Ⅰ的POC集.

(1)

无约束支链Ⅱ、Ⅲ的POC集与Ⅰ相同.

(2)

(d)确定动平台POC集.

(3)

值得一提的是,这里虽然有6个元素,但是不一定全部独立,而POC集的独立元素数目由自由度决定,需进一步求解机构的自由度.

2.2 机构的自由度计算

(1)并联机构的全周DOF公式为

(4)

(5)

(2)确定机构的自由度

(a)确定由SOC1和SOC2组成的第一回路及其独立位移方程数ξL1.

Loop1:{-P2-P3-B1-B2-P4-P5-P6-},

由式(4)得

(6)

(b)确定子并联机构的自由度及POC.

由式(5)得

(7)

该子并联机构的POC集为

(8)

(c)再确定由上述子并联机构和支链Ⅲ构成的第二条回路及其独立位移方程ξL2.

(9)

(d)确定机构的自由度.

(10)

由于新机构DOF=5,Mpa只能有五个独立元素.因此,可从Mpa的六个元素中,任取五个为独立元素,其余一个为非独立元素,组成的方案有:

(3)判断机构消极运动副

已知机构的自由度为5,由消极运动副的判定准则(若新机构的自由度小于原机构的自由度,则选取的移动副为消极运动副)判断P2副是否为消极运动副.

①假设刚化P2副,得到一个新机构,第一条支路的拓扑结构改变为HSOC1{-P(5B-P)-B1-}. 由串联机构POC方程,其末端构件POC集为

(11)

②确定新机构的自由度.

(a)确定第一回路及其独立位移方程数ξL1.

Loop1:{-P3-B1-B2-P4-P5-P6-},

(12)

(b)确定子并联机构的自由度及POC.

(13)

(c)该子并联机构的POC集为

(14)

(d)再确定由上述子并联机构和支链Ⅲ构成的第二条回路及其独立位移方程ξL2.

Loop2:{-P7-P8-P9-B3-R{-B1-B2-}-}

(15)

(e)新机构的自由度.

(16)

由于新机构DOF(F*=4)小于原机构的DOF(F=5),按照消极运动副判定准则,P2副不是消极运动副,同理可证明所有运动副都不是消极运动副.

(4)选取机构驱动副

基于驱动副判定准则(若新机构的自由度为0,则选取的运动副可同时为驱动副),判断P2、P3、P4、P5与P6副是否同时为驱动副,假设刚化P2、P3、P4、P5与P6副,得到一个新机构. 此时,支链的拓扑结构改变为:

①混合支链Ⅰ的拓扑结构等效表示为HSOC1{-B1-},混合支链Ⅱ、Ⅲ的拓扑分别为HSOC2{-B2-}、HSOC3{-P(5B-3P)-P(5B-3P)-P(5B-3P)-B3-}.

由串联机构POC方程可知,其末端构件POC集如下:第一、二支路SOC的POC集为

(17)

②确定新机构的自由度.

(a)确定由SOC1和SOC2组成的第一回路及其独立位移方程数ξL1.

Loop1:{-B1-B2-},

(18)

(b)确定由SOC1和SOC2组成的子并联机构的自由度及POC.

(19)

(c)该子并联机构的POC集为

(20)

(d)再确定由上述子并联机构和支链Ⅲ构成的第二条回路及其独立位移方程ξL2.

Loop2:{-P7-P8-P9-B3-R{-B1-B2-}-},

(21)

(e)新机构的自由度.

(22)

由于新机构DOF(F*=0),按照判定准则P2、P3、P4、P5与P6副可同时为驱动副.

2.3 耦合度计算

(a)基于机构拓扑结构分解算法,任一机构可依次分解为v个SOCi并得到其相应的约束度Δi,第j个SOCj的约束度为

(23)

进一步地,一组有序的v个SOC可划分成一个独立回路数为v的最小子运动链,它仅含1个零自由度BKC,进一步地,对一个SKC而言,须满足

(24)

因此,耦合度为

(25)

式中,mi为第i个SOCi的运动副数,Ij为第j个SOCj的驱动副数.

(b)确定机构的耦合度

耦合度可以作为评价正运动学复杂度的一个指标[13].为了评估并联机构的耦合度,必须将机构分解为多个SOC和独立回路. 如图6所示,红色双箭头表示该移动副为驱动副,不同颜色用来区分分解的各个回路,分解的具体流程如下:第一个独立回路Loop1可以通过固联SOC1的两端构件来定义,而第二个独立回路Loop2则是通过将Loop1作为子运动链,并将SOC2的两端构件连接到Loop1来实现的. 类似地,其他独立的回路Loopi(i=3～9)是通过将SOCi(i=3～9)的两端构件连接到Loopj(j=2～8)来定义(参见图6).

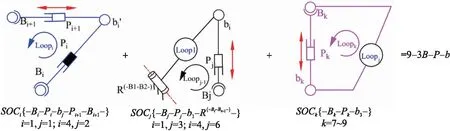
图6 9-3并联机构构型分解Fig.6 Configuration decomposition of 9-3 parallel mechanism

①第1个回路SOC1{-B1-b1-P2-B2-}的约束度为

(26)

②第2个回路SOC2{-R{B1-B2}-b1-P3-B3-}的约束度为

(27)

计入绕(-B1-B2-)副的球心连线的局部转动自由度R{B1-B2},但未计含绕b1与B3副球心连线的局部自由度.

③第3个回路SOC3{-B4-P4-b2-P6-B6-}的约束度为

(28)

④第4个回路SOC4{-B5-P5-b2-}的约束度为

(29)

⑤第5个回路SOC5{-B7-P7-b3-}的约束度为

(30)

⑥第6个回路SOC6{-B8-P8-b3-}的约束度为

(31)

⑦第7个回路SOC7{-B9-P9-b3-R{-b2-b1-}-}的约束度为

(32)

⑧第8个回路SOC8{-b1-b2-}的约束度为

(33)

⑨由BKC的判定方法,其耦合度为

(34)

(c)自由度类型

由于图3所示并联机构包含8个BKC,按照自由度类型判定准则(机构的DOF个驱动副位于不同的SKC中,机构具有部分自由度),可知该机构具有部分自由度.

(d)运动输入-输出解耦性

并联机构动平台的方向与位置是运动输入的函数,即

(35)

式中,Mpa为动平台的方向变量,x(θ1,…,θF),y(θ1,…,θF),z(θ1,…,θF)为动坐标系原点在定坐标系的位置变量,α(θ1,…,θF)β(θ1,…,θF)γ(θ1,…,θF)为动坐标系原点在定坐标系的方向变量,θi为第i个运动输入量,F为机构的自由度.

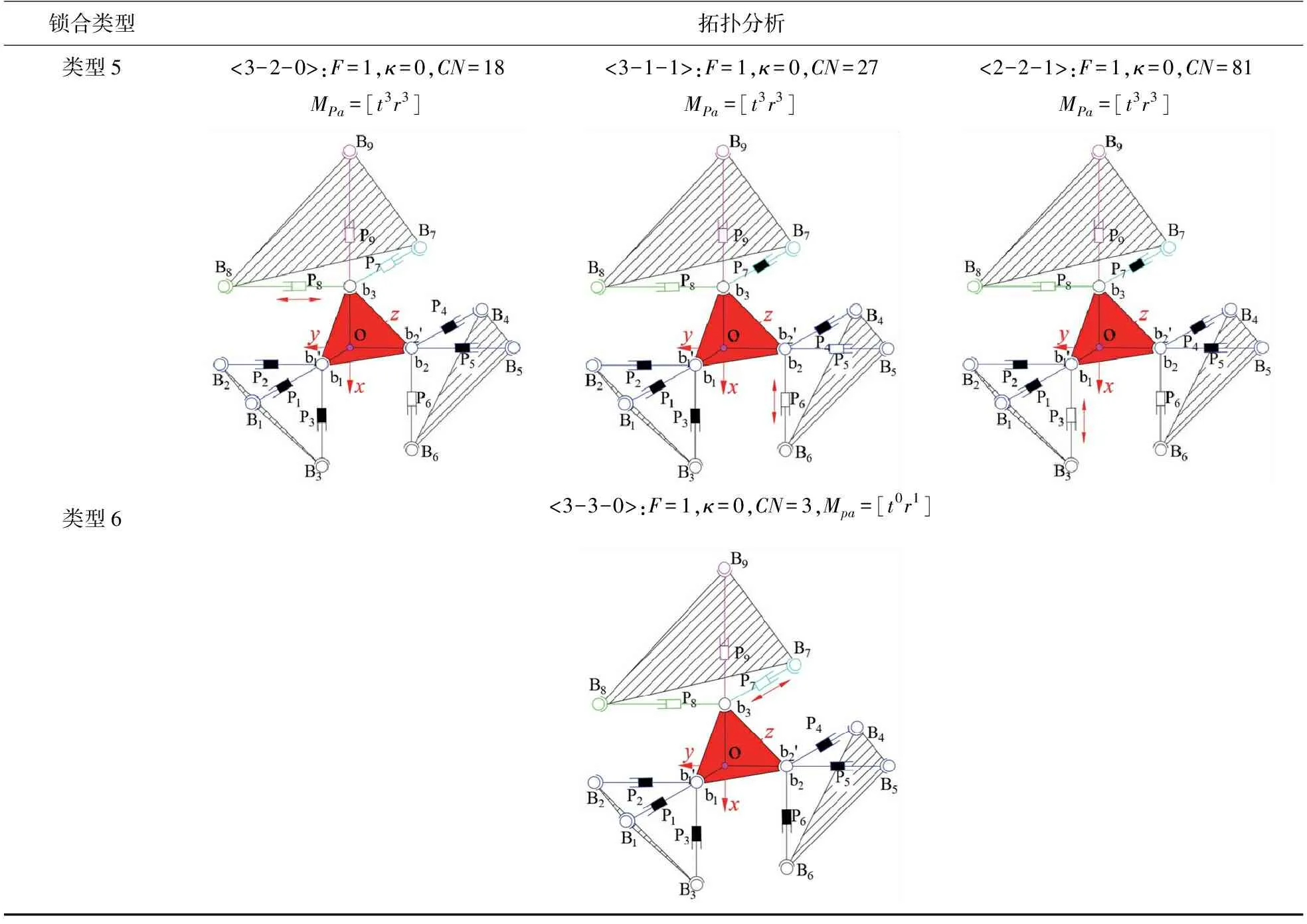
由式(35)可知,当动平台的部分方位变量只是部分运动输入量(r

3 六类锁合并联机构及其拓扑分析

根据设计的一种可转换主、从运动以及锁合的移动副,将结构中的移动副分别设置为锁合1个、2个、3个、4个、5个和6个,共六类锁合类型,重构出13种拓扑结构,如表1所示. 第2章以<1-0-0>类型(共有9种配置(CN=9))为例,基于方位特征(POC)和有序单开链(SOC)的并联机构拓扑结构设计理论,详细剖析了机构的POC集、自由度(F)、耦合度(κ)这3个主要拓扑特性指标. 对于另外12种拓扑构型. 它们的拓扑分析与计算过程与类型1相同,限于篇幅,不再详细推导,直接给出了它们的CN、F、κ和POC这4类指标的结果. 其中,类型1～5中的POC元素并不是完全独立的,而独立元素的个数等于它们的自由度个数;对于<3-3-3>与<3-0-0>构型,可确定具体的独立元素.

从表1中可以看出

表1 可重构并联机构的拓扑结构特征Table 1 Topology characteristics of reconfigurable parallel mechanism

(1)类型1～5中,机构的自由度个数与锁合移动副的个数之和都为6,且都存在3个被动支链,因此,在保持动平台输出运动不变的情况下,可简化结构,便于对其结构进行拓扑分析.

续表1Table 1 continued

(2)类型1～6中的耦合度值κ都为0,基于方位特征理论可知,耦合度值κ的大小与机构运动学求解难易性有关,耦合度值κ越大,机构运动学求解越复杂,对于耦合度值κ=0的机构可容易直接求解其解析正解.

(3)类型1～6中的13种构型,<1-0-0>与<2-0-0>分别有9种配置方式,<1-1-0>、<1-1-1>、<2-2-0>与<3-1-1>分别有27种配置方式,<3-0-0>与<3-3-3>分别有3种配置方式,<2-1-1>与<2-2-1>分别有81种配置方式,<2-1-0>有54种配置方式,<3-1-0>与<3-2-0>分别有18种配置方式,这表明该类型机构具有多构态,多功能作用.

4 结论

针对传统并联机构的工作空间有限以及具有固定的运动副问题,本文设计了一种可转换主、从运动以及锁合模式的移动副,将机构中的移动副分别设置为锁合1个、2个、3个、4个、5个和6个,共6类锁合类型,重构出13种拓扑结构,再基于方位特征(POC)和有序单开链(SOC)的并联机构拓扑结构设计理论与方法,得到了13种拓扑结构的POC集、自由度(F)、耦合度(κ)及配置个数(CN)这4个主要拓扑特性指标,研究分析表明,本文重构得到的13种构型的耦合度κ值均为0,表明了机构的可容易直接求解其解析正解,并且利用所设计的移动副装置,很方便的对并联机构进行构型转换,大大提高了并联机构的通用性和适应性.接下来的工作将研究不同构型各自所适用的工作环境以及并联机构随着环境改变去选择最优的拓扑构型.