OpenVX 高效能并行可重构运算通路的设计与实现

王 宇，李 涛，邢立冬，冯臻夫

（西安邮电大学 电子工程学院，西安 710121）

0 概述

近年来，随着电子计算机及半导体技术的快速发展，图像处理与计算机视觉（Computer Vision，CV）作为计算机应用领域中的重要分支，在军事、医学、地质勘探、多媒体等领域应用广泛［1］。由于人们对流畅视觉画面及视觉感受的要求越来越高，图形图像处理器设计及基于加快图像数据处理速度的计算机视觉算法优化不断面临新的挑战［2］。

OpenVX 标准［3］能为跨平台加速计算机视觉处理提供参照，从而实现计算机视觉处理性能和功耗的优化。其作为图像处理、图计算、深度学习和图形预处理或辅助处理的标准，被诸多芯片企业（如NVIDIA、AMD、Intel、TI、Apple 等）采用，具有广泛的应用前景。通过对OpenVX 硬件设计进行调研，发现国内目前专门为OpenVX 设计的硬件芯片较少。YAN 等［4］采用多态阵列架构（PAAG）处理器实现了OpenVX 核函数中的像素级图像处理。HUANG 等［5］针对人脸识别项目中的预处理操作，提出基于OpenVX 的并行化处理方法。TAGLIAVINI等［6］介绍一个快速设计和优化OpenVX 应用程序的框架，SAJJAD 等［7］提出将视觉通道的OpenVX 图形级规范（graph-level specification）合成优化的FPGA框架，ABEYSINGHE［8］提出一种基于性能模型的方法以优化OpenVX 图形。以上方法均没有给出底层核函数的硬件加速设计方案，缺少实现OpenVX 核函数的具体数据通路映射及分析。

本文设计一种支持OpenVX 1.3 标准的并行可重构数据通路运算器，通过配置指令重构数据通路完成图像处理任务。此外，通过研究OpenVX 中大量kernel 函数算法，并采用相应的映射方案对不同类别的函数进行数据通路映射，从而设计出适合不同类别函数的数据通路运算器。

1 OpenVX 介绍

OpenVX中的图概念如图1所示，将OpenVX 中每一次对图像的基本操作看成整个流程中的一个节点（node），该节点通过处理前后的图像和其他node相连，形成图（graph）。OpenVX 提供了一种自定义节点机制，用户可根据需要编写节点，并最终融合成图。OpenCV 是一套完整的计算视觉软件系统，提供了图像处理的底层操作，虽然其有底层硬件加速函数（HAL），但OpenVX 提供了一套更全面且结合了图计算（Graph Computing）方式的标准。

图1 OpenVX 中的图概念Fig.1 Graph concept in OpenVX

OpenVX 计算视觉标准支持最基本的图像处理和计算视觉函数。OpenVX 中多数kernel 函数是针对图像的像素级处理，这些kernel 函数构成了一个适用于硬件加速的函数子集［9］。这些像素级处理包括点处理、局部处理、全局处理、特征提取4 大类。OpenVX 1.3 支持的kernel 函数中包含的数据类型如表1 所示。

表1 OpenVX 1.3 支持的数据类型Table 1 Data types supported by OpenVX 1.3

2 OpenVX 函数的数据通路映射及分析

通过对不同函数进行相应数据通路的映射，使各个函数均具备高效的处理性能，得出不同函数实现所需运算器的种类及数目后，才能进行整体可重构数据通路运算器的设计。OpenVX 1.3 标准中共包含58 个kernel 函数，本文映射函数的数据通路中包含点处理类27 个，局部处理类10 个，全局处理类7 个，特征提取类7 个。由于相同种类函数的数据通路相似，本文着重介绍点处理中的基本运算类、图像色系变换、仿射变换、透视变换、图像局部处理中的Sobel 3×3、图像全局处理中的均值及图像特征提取中的Canny 边缘检测，并根据相应函数的映射方案和时序图对整体数据通路运算器所需的运算单元进行分析。

2.1 数据通路映射方案

数据通路映射方案包含流水线数据通路、并行数据通路、并行结构结合流水线数据通路。

1）流水线数据通路

流水线处理电路［10］采用面积换取速度的思想，可以大幅提高电路的工作频率，尤其对于图像处理任务中的二维卷积运算、图像滤波器、色系变换等。采用流水线设计可以保证一个时钟输出一个像素。由于对大部分图像处理任务而言，处理过程均采用串行的处理思路，因此流水线是较好的设计方式［11］。如图2 所示为典型的流水线结构，每个步骤独立为一个单独的处理单元，与其他处理单元同时运行，提高速度的同时也降低了设计的复杂度。

图2 流水线处理结构Fig.2 Pipeline processing stucture

2）并行数据通路

在并行处理电路［12］中，多组并行排列的子电路同时接收整体数据的多个部分进行并行计算。并行处理电路的结构如图3 所示，对每个处理数据支路均生成对应的处理电路，这样虽然提高了整体电路的处理速度，但是却造成了更大的资源消耗，即用面积换取速度。

图3 并行处理电路结构Fig.3 Parallel processing circuit structure

3）并行结构结合流水线数据通路

并行处理电路中的子电路可以是简单的组合电路，也可以是复杂的时序电路，例如上面提到的流水线数据通路。如果受逻辑资源限制，无法同时处理全部数据，也可以依次处理部分数据直到完成全部数据的处理［13］。

2.2 函数映射

2.2.1 点处理函数映射

点处理函数映射包含基本运算类映射、图像色系变换和仿射变换。

1）基本运算类映射

基本运算类包括算术类运算和逻辑类运算。算术类运算包括绝对差、算术加法和算术减法，数据类型为vx_unit8 和vx_int16。算术类运算可以通过配置指令将加法器配置为8 位或16 位定点加法或减法器进行并行计算，并输出计算结果。逻辑运算类包括按位与、按位或、按位异或、按位非和逻辑移位。本文采取数据通路的合并，即逻辑类运算操作和加法操作进行数据通路的合并，以减小整体电路的面积。对于一个32 位的基本运算器，通过指令配置，可以在每个时钟周期并行完成2 个16 位或4 个8 位的算术类运算或逻辑类运算。

2）图像色系变换

该函数可以实现颜色的转换，将指定格式的图像转换成另一种格式。以RGB 线性转换为例，转换公式如式（1）所示：

其中：R1、G1、B1代表原来的颜色通道；R2表示新的R通道。

对其进行数据通路映射如图4 所示，分为3 级流水线：第1 级并行计算式（1）中的3 个乘积项；第2 级把前2 个乘积项结果送入加法器a0，并把第3 个乘积项进行寄存；第3 级把a0和寄存器值相加，并移位输出。由图4 可知，色系变换的流水线数据通路需要3 个定点乘法器及2 个定点加法器。

图4 色系变换流水线Fig.4 Color convert pipeline

3）仿射变换

仿射变换对图像进行仿射运算，支持的数据类型为vx_unit8和vx_float32。该函数使用2×3的仿射矩阵M对输入像素进行仿射变换，具体计算如式（2）～式（4）所示：

仿射变换数据通路的映射如图5 所示，第1 级使用4 个浮点乘法器并行计算式（2）和式（3）中的乘积项；第2级将4个输出结果两两相加；第3 级 将M1，3、M2，3分别和a0、a1相加并输出最终计算结果。由图5可知，仿射变换的流水线数据通路需要4 个浮点乘法器及4 个浮点加法器。

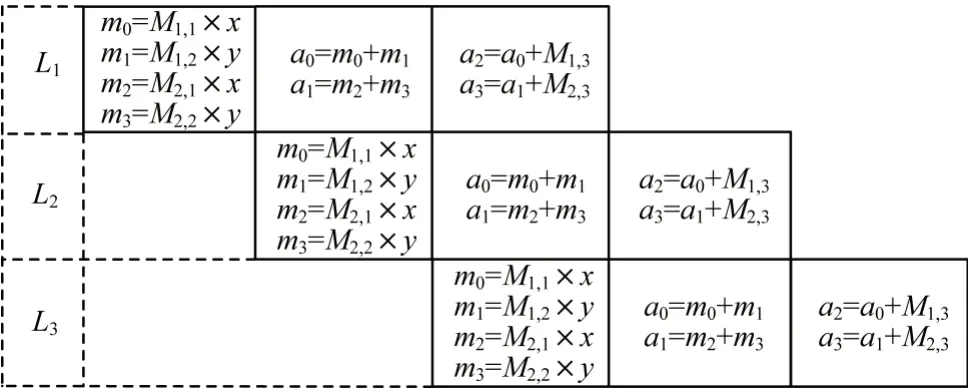
图5 仿射变换流水线Fig.5 Affine transformation pipeline

透视变换对输入图像进行透视变换运算，支持的数据类型为vx_unit8 和vx_float32。该函数使用3×3 的透视矩阵M对像素进行透视变换，具体计算如式（5）～式（8）所示：

对其进行数据通路的映射如图6 所示，分为4 级流水线：第1 级并行计算式（5）～式（7）中的乘积项；第2 级并行计算 式（5）～式（7）中的第1个加法；第3 级并行计算式（5）～式（7）中的第2 个加法；第4级并行计算x0/z0，y0/z0。由图6 可知，透视变换的流水线数据通路映射需要6 个浮点乘法器、6 个浮点加法器、2 个浮点除法器。

图6 透视变换流水线Fig.6 Perspective transformation pipeline

2.2.2 局部处理函数映射

Sobel 图像滤波支持的数据类型为vx_unit8，当滤波模板大小为3×3 时，需要将9 个像素p0～p8进行计算，其流水线数据通路如图7 所示：第1 级并行计算8 个像素的加法，第2 级将上一级的结果两两相加，第3 级将上一级的结果相加，第4 级对最后一个像素进行加法计算并得出最终结果。由图7 可知，Sobel 3×3 滤波流水线电路需要8 个定点加法器。

图7 Sobel 滤波流水线Fig.7 Sobel filter pipelined

本文通过电路的扩展和配置指令，可将中间结果写回寄存器堆或输出，实现滤波模板大小的可配置，其扩展性和兼容性更好。当滤波模板大小为5×5 时，使用上述的流水线通路一次可计算9 个像素值，而5×5 模板需要计算邻域内25 个像素值，需要循环此数据通路3 次。在前2 次循环中，需要将计算的中间结果写回寄存器堆2 次，读出寄存器堆2 次，第3 次循环结束时完成计算。对于7×7 的模板，需要写回寄存器堆5 次，读寄存器堆5 次，第6 次循环结束后完成计算。

2.2.3 全局处理函数映射

在进行全局参数计算时，由于运算器的资源有限，有时需要将部分计算或比较结果存入寄存器堆中。以计算输入图像的均值为例，输入数据的类型为vx_unit8，输出数据的类型为vx_float32。均值的计算如式（9）所示：

由于实现Sobel 3×3 滤波流水线电路需要8 个定点加法器，因此进行平均值计算最多需要8 个定点加法器约束，平均值计算采用并行结构结合流水线的的数据通路映射方案，如图8 所示。映射过程为：第1 级对4 行像素并行累加计算，每1 行计算结束后进行换行操作，一直迭代到最后一行像素；第n+1 级用a4、a5对4 个累加结果两两计算；第n+2 级计算a4、a5的和以及W×H；第n+3 级计算浮点除法。完成平均值并行计算需要7 个定点加法器、1 个定点乘法器及1 个浮点除法器。

图8 并行计算均值Fig.8 Parallel computing mean

2.2.4 特征提取类函数映射

Canny 边缘检测计算过程相对复杂，需要将中间结果写回存储中，处理过程主要分为3 步：梯度幅值和方向计算，非极大抑制及边缘追踪。

1）梯度幅值和方向计算

将输入图像与指定大小的垂直和水平方向的Sobel 算子进行卷积，使用两个定向梯度图像Gx和Gy计算梯度大小和梯度方向。当计算梯度的类型为VX_NORM_L1 时，梯度幅值为|Gx|+|Gy|。由于arctan(x)计算复杂，且在非极大值抑制中只需知道像素的梯度方向在哪块区域即可，不需要求出实际的角度。因此，本文根据Gx、Gy的倍数关系及符号判断梯度方向，将梯度方向划分为4 个区域path_1、path_2、path_3 和path_4。计算梯度幅值和方向具体数据通路的映射如图9 所示。其中：第1 级利用Sobel 算子计算水平、垂直方向的梯度幅值Gx和Gy以及符号类型；第2 级计算梯度幅值G，判断path_1 及path_3 的类型；第3 级判断path_2及path_4 的类型；第4 级把梯度幅值及梯度类型写回存储中。

图9 梯度幅值和方向计算Fig.9 Calculation of gradient amplitude and direction

2）非极大抑制

非极大抑制是仅当检测像素的梯度大小在垂直于其边缘方向上大于或等于像素时，才将检测像素保留为潜在边缘像素。例如，当像素的梯度方向为0°时，则其梯度幅值大于像素为90°和270°时的梯度幅值，才保留像素作为边缘。非极大抑制的映射过程为：第1 级从缓存中读出当前像素梯度及邻域内8 个像素的梯度值及梯度方向类型｛path_4，path_3，path_2，path_1｝；第2级根据｛path_4，path_3，path_2，path_1｝的值分别在4个方向进行像素梯度幅值的比较，并输出比较结果；第3级将比较结果写回存储中。

3）边缘追踪

输出图像的最终边缘通过双阈值法进行识别。所有梯度幅度大于高阈值的像素均标记为已知边缘像素（非0），小于等于低阈值的像素赋0。对于高阈值和低阈值间的像素使用8 连通区域确定，只有与高阈值像素连接时才被视为边缘点。边缘追踪的映射过程为：第1 级从存储中读出非极大抑制后像素比较的结果；第2 级对大于高阈值的像素值直接赋255；大于低阈值的像素值进行8 个邻域像素值与高阈值进行比较，若大于高阈值，则输出255，否则输出0。

2.3 所需运算单元分析

所需运算单元的分析如下：

1）所需运算单元种类的分析

由表1 可知，OpenVX 1.3 支持定点和浮点数据类型，所以设计的数据通路运算器中需要包含定点计算单元和浮点计算单元。根据上述函数的映射方案可知，色系变换中需要用到定点加法和定点乘法运算，仿射变换需用到浮点加法和浮点乘法运算，透视变换需用到浮点加法、浮点乘法和浮点除法计算，均值计算需用到定点加法、定点乘法、定点除法和浮点除法计算，Sobel 需要用到定点加法计算。综上，设计的数据通路运算器需包含定点加法器、定点乘法器、定点除法器、浮点加法器、浮点乘法器和浮点除法器。

2）所需运算单元数目的分析

由于采用不同数目运算器构建的流水线映射方案不同，处理不同函数所需的时间也不同，因此需要用时序图排序来分析各种OpenVX 函数是否达到或者接近最佳性能。当采用不同个数的运算器时，分别对色系变换函数、仿射变换函数、均值计算函数、Sobel 滤波函数进行时序图的排序分析。

色系变换时序图如图10 所示。由图10（a）可知，当采用1 个定点乘法器和2 个定点加法器时，色系变换函数在第5 个时钟周期时处理完第1 个像素，流水线输出时每隔2 个时钟周期输出1 个像素。由图10（b）可知，当采用2 个定点乘法器和2 个定点加法器时，色系变换函数第5 个时钟周期处理完第一个像素，流水线输出时每隔1 个时钟周期输出一个像素，处理性能较好。由图10（c）可知，当采用3 个定点乘法器和2 个定点加法器时，色系变换第3 个时钟周期处理完第1 个像素，流水线输出时每个时钟周期产生1 个像素，处理性能最好。

图10 色系变换时序图Fig.10 Sequence diagram of color convert

仿射变换时序图如图11所示。由图11（a）可知，当采用1个浮点乘法器和4个浮点加法器时，仿射变换处理在第5个时钟周期时处理完第1个像素，流水线输出时每隔4个时钟周期输出1个像素。由图11（b）可知，当采用2个浮点乘法器，4个浮点加法器时，仿射变换处理在第4个时钟周期时处理完第1个像素，流水线输出时每个时钟周期产生1个像素，处理性能较好。由图11（c）可知，当采用4个浮点乘法器、4个浮点加法器时，仿射变换处理第3个时钟周期处理完第一个像素，流水线输出时每个时钟周期产生一个像素，处理性能较好。

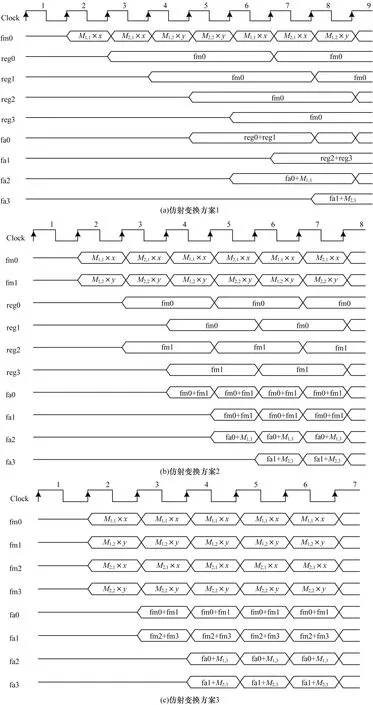
图11 仿射变换时序图Fig.11 Affine transformation sequence diagram

Sobel滤波时序图如图12 所示。由图12（a）可知，当采用4个定点加法器时，Sobel 3×3滤波在第7个时钟周期时处理完第一个像素，流水线输出时每隔1个时钟周期产生1 个像素。由图12（b）可知，当采用6 个定点加法器时，Sobel 3×3 滤波在第6 个时钟周期时处理完第1 个像素，流水线输出时每隔1 个时钟周期产生1 个像素，处理性能较好。由图12（c）可知，当采用8个定点加法器时，Sobel 3×3 滤波在第4 个时钟周期时处理完第1 个像素，流水线输出时每个时钟周期输出1 个像素，处理性能最好。

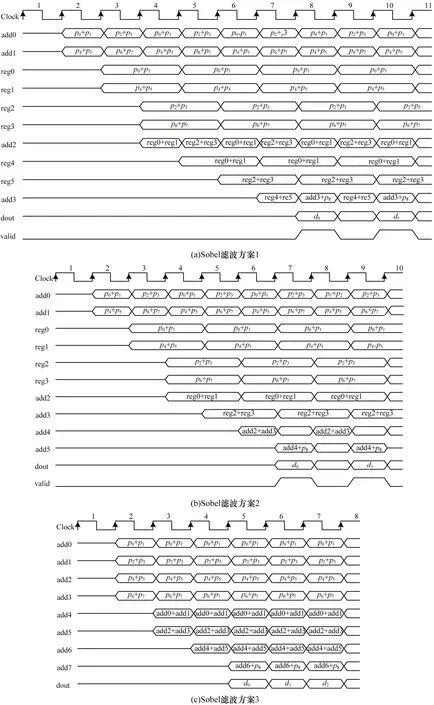
图12 Sobel 滤波时序图Fig.12 Sobel filtering sequence diagram

均值计算时序图如图13 所示。由图13（a）可知，当采用1 个定点加法器、1 个定点乘法器、1 个浮点乘法器时，均值计算函数在第11 个时钟周期时处理完第1 个像素，流水线输出时每隔9 个时钟周期完成1 次均值计算。由图13（b）可知，当采用3 个定点加法器、1 个定点乘法器、1 个浮点乘法器时，均值计算函数第6 个时钟周期处理完第1 个像素，流水线输出时每隔4 个时钟周期输出1 个像素，处理性能较好。由图13（c）可知，当采用7 个定点加法器、1 个定点乘法器、1 个浮点乘法器时，均值计算函数第4 个时钟周期处理完第1 个像素，流水线输出时每隔2 个时钟周期输出1 个像素，处理性能最好。

图13 均值计算时序图Fig.13 Mean calculation sequence diagram

从函数处理的性能和电路面积以及电路的可编程性、灵活性考虑，确定定点加法器数目为8 个，定点乘法器数目为4 个，定点除法器数目为2 个，浮点加法器数目为4 个，浮点乘法器数目为2 个，浮点除法器数目为2 个，从而满足上述函数的高效通用处理要求。

3 数据通路运算器的设计

3.1 数据通路运算器的整体结构

根据OpenVX 1.3 中各类函数的实现方法，将所需计算单元进行分析后，设计出的OpenVX 并行可重构数据通路运算器［14-15］如图14 所示，包括基本运算单元（arithmetic unit）、数 据 交 叉 互 联 模 块（cross-bar interconnect）、指令配置模块（ins_config）、指令存储（ins_cache）、数据寄存器堆（register file）和读/写控制模块（rd/wr_ctl）。基本运算单元的设计是根据具体函数的映射要求，将加法器和乘法器设计为并行可拆分的结构，以适应多种数据格式的要求。数据通路运算器的执行过程如下：指令配置单元从指令存储中取出相应的指令，发送给数据交叉互联模块、rd/wr_ctl 单元和基本运算单元。rd/wr_ctl 模块根据指令从寄存器堆中取出相应的运算数据并进行译码及截位处理，并输出到交叉互联电路。交叉互联电路根据相应的配置信息将数据送入运算单元。运算单元根据相应指令配置进行计算，并将计算结果写回到交叉互联电路或输出。

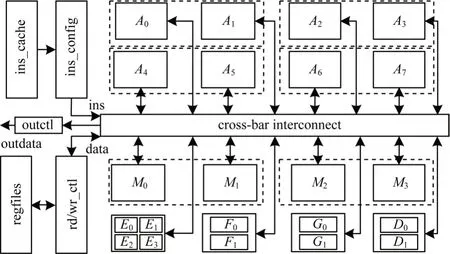
图14 数据通路运算器的总体结构Fig.14 Overall structure of the data path arithmetic unit

数据通路运算器支持的计算类型和计算速度直接影响整体处理器的性能参数［16］。本文设计的数据通路运算器共有22 个基本计算单元，包括：8 个定点加法器（A0～A7），4 个定点乘法器（M0～M3），2个定点除法器（D0，D1），4个浮点加法器（E0～E3），2个浮点乘法器（F0，F1）及2个浮点除法器（G0，G1）。各运算单元之间采用数据通路合并、功能单元共享、电路资源复用等方法，以减少整体面积占用［17］。各运算单元支持多种数据类型，定点计算单元支持8位有/无符号数、16位有/无符号数、32位有/无符号数的运算，浮点单元支持32 位浮点数的运算。

3.2 子模块内部结构

3.2.1 定点单元设计

定点单元支持的计算类型包括定点算术类和定点逻辑类计算，其中定点算术类计算包括定点加、减、乘、除、绝对值和比较。定点逻辑类计算包括逻辑与、逻辑或、逻辑非、逻辑异或和逻辑移位。

1）定点加法器

定点加法器的设计依照数据通路的映射方案及数据类型，根据指令配置可并行计算2 个32 位，或4 个16 位，或8 个8 位的有符号、无符号数定点加法。加法运算的关键路径在进位链上［18］，为缩短这一关键路径，加法器的设计采用进位选择加法器（CSA），并设计基本单元为8 位的进位选择加法器。

2）定点乘法器

定点乘法器的设计采用混合乘加结构（Fused Multiply Add，FMA），依照数据通路的映射方案及数据类型，混合乘加运算器可根据控制信号完成32 位的混合乘加运算，支持2 组32 位、4 组16 位、8 组8 位定点数的加法或乘法运算，提高数据并行计算的能力。采用混合乘加运算数据通路，可以减小逻辑电路大小。混合乘加器的电路设计如图15 所示，功能复用上述的进位选择加法器，从而减少整个电路的面积。混合乘加器可根据控制信号对加法进位链进行截断，并输出相应的加法计算结果或乘法计算结果。

图15 混合乘加器结构Fig.15 Fused multiply adder structure

3）定点除法器

定点除法器的设计采用牛顿迭代（Newton Raphson）算法［19］，该算法利用乘法运算代替除法运算，算法的主要步骤为求1/b，设f(x)=1/x-b，则在x=1/b处f(x)=0。应用牛顿迭代公式，可得：

传统的牛顿迭代除法器将式（10）中的2 次乘法和1 次加法并行计算，增加了路径延迟，具体电路如图16所示。本文在其基础上做的改进如图17 所示，设计中复用定点运算中的定点加法和定点乘法模块，从而加快运算速度；针对迭代运算，将乘法和加法计算拆分为3 级流水线，以缩短路径延迟及提高运行速率。

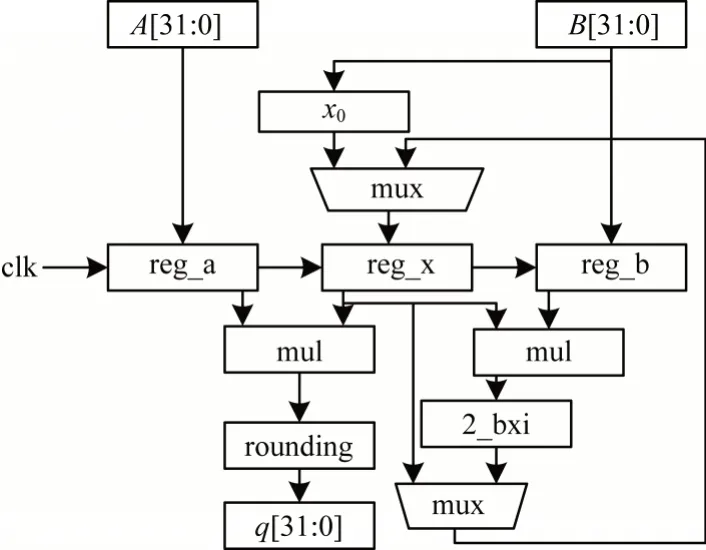
图16 传统的牛顿迭代除法器Fig.16 Traditional newton raphson divider

图17 改进的牛顿迭代除法器Fig.17 Improved newton raphson divider

3.2.2 浮点单元设计

浮点单元设计如下：

1）浮点加法器

浮点加法器支持单精度浮点运算类型，包括浮点加、减定浮点转换。浮点加法器设计为3 级流水线：操作数阶码对齐、尾数计算级、输出结果规格化。流水线浮点加法器可以在每个时钟周期接收一条浮点加法或减法指令［20］。

2）浮点乘法器

浮点乘法器是在Booth 算法、Wallace 树型结构［21］以及进位选择加法器基础上，设计为3 级流水线，具体电路如图18 所示。第1 级流水线通过异或门计算乘数和被乘数的符号位。第2 级流水线将乘数的指数部分和被乘数的指数部分偏置相加，根据溢出情况和尾数最高位调整指数后对指数规范化处理，此外，采用基4 的Booth 算法减少部分积的个数，用Wallace 树形乘法器计算部分积。第3 级流水线完成尾数部分的计算及调整输出结果。

图18 浮点乘法器Fig.18 Floating point multiplier

3）浮点除法器

浮点除法器的设计采用基于牛顿迭代算法的流水线浮点除法器，尾数计算部分采用24 位牛顿迭代除法器模块。浮点除法器的设计如图19 所示，其流水线划分为4 级：牛顿迭代计算，部分积计算，定点加法运算和规格化输出。

4 实验结果与分析

4.1 实验结果

通过Modelsim SE-64 10.4 仿真验证平台编写相应的测试程序，并对色系变换、腐蚀、膨胀、Sobel和Canny边缘检测函数进行功能仿真，实验结果如图20 所示。其中，图20（a）表示未经处理的640 像素×480 像素的原图像，图20（b）表示经过色系变换后得到的结果，图20（c）表示经过腐蚀操作后的结果，图20（d）表示经过膨胀操作后的结果，图20（e）表示经过Sobel 3×3 滤波后的结果，图20（f）表示经过Canny边缘检测后的结果。由图20可知，使用不同算法在测试程序上进行功能仿真，均可达到预期处理目的，且和软件处理结果相同。

图20 不同函数的功能仿真结果Fig.20 Functional simulation results of different function

将上述函数的算法在数据通路运算器上进行映射后，对每秒处理后的图像帧数进行统计如表2 所示。由表2可知，当屏幕刷新率为640像素×480像素@60 Hz，800像素×600像素@60 Hz，1 024像素×768像素@60 Hz及以下标准时，色系变换、Sobel、腐蚀和膨胀均可达到快速刷新并显示的要求。

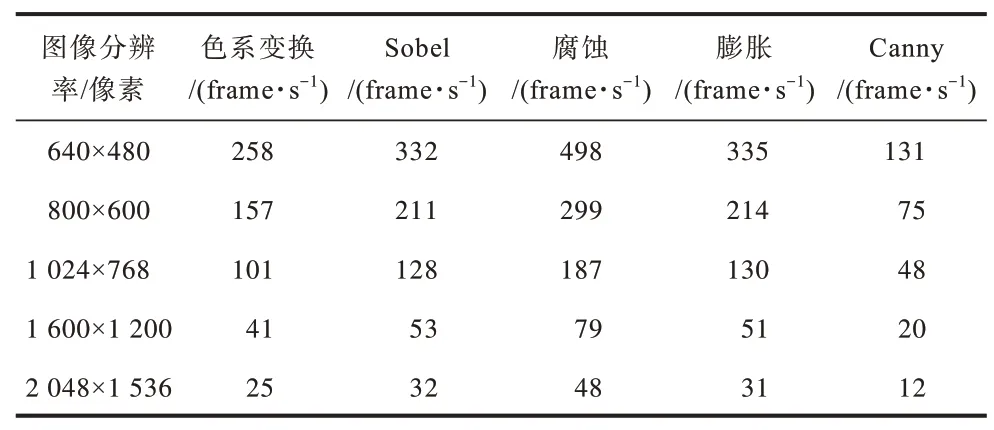
表2 不同分辨率下每秒处理的图像帧数Table 2 Image frames per second processed under different resolutions

当处理图片的分辨率在1 600 像素×1 200 像素、2 048 像素×1 536 像素及以上时，单个数据通路运算器无法满足实时性及高速率的通用图像处理要求，此时需要将多个数据通路运算器采用互联拓扑结构组合构成OpenVX 并行处理器，在并行处理器上获得处理性能的提升，达到实时处理的目的。

4.2 性能分析

采用Synopsys 公司综合工具Design Compiler，链接SMIC 65nm CMOS 工艺库对整体电路及各运算器进行综合实现，并得到时序报告、面积报告和功耗报告。对于32 位的除法运算，本文改进的牛顿迭代除法器最大主频可达520 MHz，相同实验条件下，对比传统的牛顿迭代除法器，其速率提升了22%。根据综合结果对整体电路进行性能分析，结果如表3 所示，电路的时延为2 ns，且1/2 ns=500 MHz，因此系统最高时钟频率达500 MHz，系统的吞吐量为1.86 GB/s。

表3 整体电路性能分析Table 3 Overall circuit performance analysis

5 结束语

本文对OpenVX 1.3 标准中kernel函数算法进行分析与映射，根据映射后电路的时序图分析运算器数目，并基于分析结果对可重构数据通路运算器构建整体结构及内部子模块。此外，对可重构数据通路运算器进行灵活编程，设计基于OpenVX 1.3 标准的kernel 函数算法，完成通用的图像处理。实验结果表明，基于OpenVX 的并行可重构数据通路运算器能满足实时及高速率的通用图像处理要求。下一步将优化各运算单元性能，通过设计处理性能更好的运算器及编写相应的微指令，实现上层复杂特征提取函数的数据通路映射。