引导学生深度学习数学的阶梯式题组教学初探——以高中数学新教材“2.2 基本不等式”一节为例

黄清钿

（大田县第五中学，福建 大田 366100）

学好高中数学，学生需要阅读课本，尝试练习，上课听讲，独立思考，顺利解题.但并不是每个学生都能自觉进行这五个方面的学习，在教学实践中，教师往往会有以下问题需要解决：1.有什么办法能让学生自觉去阅读课本？2.有什么办法能让学生自觉去尝试完成课本或练习册中的练习？3.有什么办法能让学生专心听课、独立思考？4.有什么办法能让学生用所学知识顺利解题？这些问题的解决能有效引导学生进入深度学习，提高学习效率.而解决这些问题需要一个载体，教师通过这个载体促使学生自觉进入深度学习.阶梯式题组便是解决上述问题的一个载体，它是由从简单到综合、从易到难形成梯度的几个问题或习题组成的一个题组.教师通过阶梯式题组教学引导学生自主阅读课本，自觉尝试练习，主动听课思考，实现学生顺利地运用所学知识解题的目标.

一、课前预习的阶梯式题组设计

阅读课文是学生理解教材的基础，而学生阅读的重点在于概念、原理及其应用.课前预习的阶梯式题组设计要有利于引导学生阅读分析教材中的概念、原理及应用，常用方法可从以下几方面进行设计：

1.设计导入问题，引导学生了解本节知识的背景，为学习新概念、新知识作铺垫

设计导入问题要依托教材中的导入内容和探究内容进行设计，有时也可选择教材外的材料，但以教材导入内容和探究内容进行设计更有利于学生对教材的阅读.设计的问题要有层次性，只要学生认真阅读教材就能找到问题的答案.例如，新教材高中数学必修1 第二章P44“2.2 基本不等式”（下同）导入问题可以进行如下设计：

（1）对∀a，b∈R，有（a－b）2≥0，比较a2＋b2 与2ab的大小（用“≥”表示）.在这个不等式中何时等号成立？

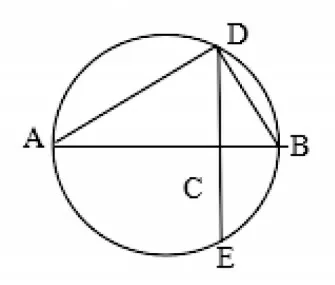
（3）如图，AB 是圆的直径，点C 是AB 上一点，AC=a，BC=b，过点C 作垂直于AB 的弦DE，连接AD，BD.利用此图说明a、b 几何平均数与算术平均数的不等关系.

这一题组从易到难，基础好的学生不看教材就能解决，基础一般的学生通过阅读教材也能顺利完成.学生完成这一题组对本节的核心内容就形成了初步的印象：两正数的几何平均数小于或等于其算术平均数.

2.设计尝试练习题，引导学生读懂关键知识点，关注课本例题在知识点应用中的示范作用

尝试练习题是检测学生阅读教材成效的一把尺子，它的设计要“好量”“可量”“量准”.所以尝试练习题的设计要紧扣概念、公式原理和例题并形成梯度，从易到难.例如“基本不等式”一节，可设计如下尝试题，让学生在预习时能独立完成.

（2）已知ab=1，a＞0，b＞0，求a+b 的最小值.

（3）已知a+b=1，a＞0，b＞0，求ab 的最大值.

（4）课本P46 练习的1-5 题，P48 的小练习1-4.

这一题组的前三题是基础题，帮助学生巩固和理解基本不等式，学生一般能较顺利地完成.第（4）题是教材的课后练习题，重点检测学生对基本不等式的应用，有一定的综合性.学生在完成尝试练习过程可能会碰到一些问题，但这些问题可让学生在课堂上产生“求解欲望”，是教师课堂解惑的重要素材.

3.设计总结式问题，引导学生读懂教材的核心内容

学生预习一节课的内容可能会泛泛而读，抓不到重点，因此教师在布置预习内容时要为学生提出总结式问题，学生可以按照这些问题在教材中寻找答案，这些问题解决了，本节内容的核心就抓住了.例如“基本不等式”一节，教师可为学生设计如下总结式问题：

（1）什么是基本不等式？怎样用两正数的算术平均数和几何平均数来表示基本不等式？

（2）怎样直接利用不等式的性质推导出基本不等式？

（3）从你所解的题型中总结出基本不等式的常见用途（不少于2 种）.

（4）运用基本不等式解决数学问题时需注意哪些运用条件？

这一题组可引导学生认真阅读课文，还能促使学生认真完成尝试练习并进行思考总结.特别是对知识点的应用，学生可能总结得不完善、不全面，但学生通过独立思考和研究便能加深对本节核心内容的理解，为教师的课堂解惑环节打下较好的基础.

二、课堂解惑的阶梯式题组教学

有了学生的课前预习，学生对所要学习的内容已有了初步的了解，知道这节课的主要内容是什么，但也存在一些不能消化的问题.因此课堂教学要为学生答疑解惑，用启发式教学帮助学生解决预习过程中存在的问题.如果只让学生自己提出存在的问题进行教学，那么这节课可能无法实现既定的教学目标，因为学生在预习过程所碰到的问题多数是“这题不会做”“这题不会答”，缺乏深层的思考性.教师要用设问的形式设计若干问题形成阶梯式问题组，引导学生提出问题并找到解决问题的办法.课堂提问的阶梯式题组教学主要从以下两个方面提问并引导学生提出问题和解决问题.

1.关于概念、公式、定理理解的提问

由于高中数学抽象性较强，一些学生对数学概念定义、公式定理的理解存在障碍.教师的提问要有利于引导学生清除这些障碍.提问时可用阶梯式问题组，一步步使学生在回答中理解概念、公式、定理.例如，“基本不等式”一节，正确理解基本不等式这个公式是本节课的关键，如何让学生更好地理解这个公式并用好这个公式，教师可以进行如下提问引导：

师：怎样表示基本不等式？

师：大家说对吗？是否缺点什么？你能补完整吗？

生1：其中a，b 均为正数.

师：基本不等式有哪些变式？公式变形后，a、b 的取值范围有什么变化？

师：还有吗？课本P46 的小练习第2 题（1）：x，y 都是正数，且x≠y，求证：.从中你可以得到什么启发？

师：很好，同学们可以再总结一些其它的常用变形，汇总在一起备用.下面，谁来说说如何推导基本不等式？

生7：直接利用不等式的性质推导，可见课本P44.

师：两位同学回答得很好.再问：基本不等式这个公式中的a，b 代表什么？举例说明.

生8：基本不等式中的a，b 可以代表两个正数，也可以代表两个大于 0 的代数式，例如+27.3；xy为正数，则.

师：很好.能否从课本例1、例2 中总结一下，基本不等式中的a，b 还可以代表什么样的代数式？

众生：和或积为定值的代数式.

师：没有条件要求吗？

众生：和或积为定值的两个代数式都必须大于0.

通过以上的启发式教学，学生对基本不等式的内容、条件、应用便有了较深刻的认识.

2.关于重要知识点应用方法的提问

学生学习的效率关键在于能否顺利应用所学的内容解题，因此课堂上教师要充分了解学生对例题的理解和尝试练习完成的情况，并引导学生总结新知识点应用的方法.由于学生总结概括的能力不同，而且通过预习只是初步了解一节课的主要内容，所以教师要有针对性地提出一些路径，让学生的总结有立足点，概括有参照点.教师可从知识应用的题型种类引导学生概括知识应用的方法，从例题、尝试题、教师讲评题的解法分析引导学生总结知识应用的方法.例如，“基本不等式”一节可以从以下几个方面提问讲解，引导学生总结概括知识点的应用.

（1）从课本例题和尝试练习中，你认为用基本不等式求最值这类题目的主要特点是什么？怎样求得这个最值？

（2）用基本不等式求最值需要注意三个条件：“一正、二定、三相等”，如何理解这句话？

（3）基本不等式的应用有哪些题型？借助教材的例题习题、练习册或辅导用书为以下四种题型配上一至二道习题并进行解答，总结其解题方法：①利用基本不等式比较代数式的大小；②用基本不等式求代数式或函数的最值；③利用基本不等式证明不等式；④用基本不等式解实际应用题.

这三个问题出示给学生后，可留一定时间让学生思考，然后引导学生回答，学生回答不出来的，教师补充讲解.其中第（3）个问题可让学生前后桌讨论交流，最后请个别学生总结回答，教师补充完善.

三、知识应用的阶梯式题组练习

数学是一门实践性很强的学科，学生每学一个知识点都少不了进行一定量的应用练习.由于学生的基础不同，学习成果各异，所以组织学生进行课堂练习或课后作业，所提供的习题必须面向全体学生，让每个学生都练有所得，并且通过练习能促进学生钻研教材或辅助用书，对一时难以完成的题目能按题索法，从教材或辅导书中寻找相似例题，分析其解法，并迁移解决教师布置的练习题中.这一过程是学生进行深度学习的有效体现，学生为解决眼前的问题必然翻动教材和相关的辅导书或者和同学讨论研究，一旦问题得到解决，既可增强学生的愉悦感，又能让学生对所学知识的应用记忆深刻.要让学生产生这种效果，设计练习题是关键，所出示的题目既不能让学生无从下手，耗费大量时间，也不能让学生轻松完成，没有丝毫挑战性.因此需要设计阶梯式题组，同一类题型至少出两题，先易后难.容易题是指绝大多数学生都能顺利完成的题目，目的是让中下生也能尝到自主学习成功的甜头；较难的题是只有一半左右的学生不能顺利完成，需要借助教材或辅导用书的相关例题示范才能完成，目的是让多数学生自主深度阅读教材或辅导用书，培养学生自主解决问题的能力.例如，“基本不等式”一节，可按题型分类设计阶梯式题组，其中用基本不等式求最值这一题型，可设计以下阶梯式题组：

A.最小值6 B.最小值8 C 最大值8 D.最大值3

（2）容易题，添项变式后直接用公式：已知x＞2，函数+x的最小值是___.

（3）中档题，公式变形后的应用：已知a＞0，b＞0，且a+2b=8，那么ab 的最大值等于（）.

A.4 B.8 C.16 D.32

（4）中档题变式，结合“1”的性质应用公式的变形：若正数a，b 满足a+b=1，则的最小值为__.

（5）较难题，添项变式及公式变形后的应用：已知a＞0，b＞0，a+b=5，则的最大值为____.

这种从易到难的阶梯式题组要结合学情设置，其中的容易题、中档题、较难题是相对而言的，不能一概而论.只要能使多数学生较顺利地完成三分之二的题目，且三分之一的题目通过进一步阅读教材或教辅书也能解决，则这样的阶梯式题组就是好题组.

四、阶梯式题组教学中需注意的问题

如前所述，阶梯式题组教学包含课前预习的问题题组，课内的问题题组所进行的启发式教学，课堂应用或课后作业的阶梯式题组练习，每个环节都需要学生花一定的时间进行自主学习思考实践.因为高中数学的逻辑性较强，前后知识的联系密切，一个小章节往往需要几个课时才能完成，如果第一课时或单独的某一个课时要进行阶梯式题组教学，有时在操作上有一定的难度，甚至无法进行，因此需要将几个课时的教学内容进行整合，进行小单元教学设计.教师在预习、课堂、巩固练习各环节中设计的阶梯式题组可在同一课时发挥作用，也可在不同课时发挥作用.根据一个小章节内容的多少和难易程度，可将整个小章节作为一个小单元进行设计，也可两三课时的内容作为一个小单元进行设计.例如，“基本不等式”一节教材安排了两个课时的内容，第一课时介绍基本不等式的内容和简单应用，第二课时举例说明基本不等式在实际问题中的应用.阶梯式题组教学可将这两个课时作为一个小单元进行设计，在预习环节就让学生阅读整个小单元的内容.要完成本小单元的阶梯式题组，学生可能会碰到比较多的问题，所以在第一节课堂上教师要结合学生的问题进行有针对性的启发式教学，让学生在第一课时扫清概念、公式、知识点简单应用等方面的基本问题，第二课时再进行阶梯式题组训练和基本不等式应用题型的拓展总结.

引导学生进行深度学习的方法多种多样，但各种方法的共同点都是要让学生动起来.在阶梯式题组教学中只要设计好题组加上教师的启发引导就能较好地让学生动脑、动口、动手，从而提高学习效率.