基于最小二乘法MEMS惯性传感器姿态解算算法

熊新炎， 黄 涛， 温子豪， 张 童

(哈尔滨商业大学 轻工学院，哈尔滨 150028)

人体姿态捕捉广泛应用于计算机游戏制作、军事训练、人体医疗康复、行为预判、动作识别等领域.传统的机械式姿态捕捉存在运动幅度受限、无法捕获较为复杂的姿态.光学式姿态捕捉系统造价昂贵，标定光点会出现遮挡，后期处理时间长[1].随着MEMS微机电技术和计算机技术的快速发展，MEMS惯性传感器在可穿戴便携设备中应用越来越成熟，低成本惯性测量单元具有体积小、质量轻、功耗低、性价比高等特点，在人体姿态捕捉系统得到普遍应用[2].由于外界噪声和磁场变化等多因素影响，MEMS惯性传感器无法长时间对姿态进行精确测量，其精度和稳定性较低[3].

本文采用三轴加速度计、三轴陀螺仪和三轴磁力计组成的9维惯性测量单元对姿态进行测量，对三轴加速度计进行标定及建立误差模型，利用最小二乘法确认误差参数[4].根据欧拉角法对倾向角和航向角分开求解特点，减小磁场变化干扰[5].再对欧拉角中奇异值问题进行改进，分为两种状态的滤波模式，克服了传统欧拉角中的奇异值问题.

1 姿态解算

常用的姿态解算方法有欧拉角、方向余弦法、四元数法.方向余弦法方程参数多，计算量较大，效率低，不方便对姿态的变化的理解.四元数法计算量小，易于操作，但易受外界磁场影响.欧拉角表达姿态形象直观，简单易懂，但会出现万向锁现象[6].由于欧拉角法求取时倾斜角和航向角分离的特点，求取的倾斜角不受外界磁场变化干扰.为此，对传统的欧拉角中奇异值问题进行改进，分为一般姿态值和奇异值状态姿态值两种滤波模式.

传感器在测量时会出现误差，例如敏感轴比例系数误差、零点偏移、外界温度等等因素会导致出现芯片灵敏度变差，测量精度不准等问题[7].对MEMS惯性传感器进行误差标定补偿.姿态解算流程图如图1所示.

1.1 三轴加速度计误差建模及标定

根据上述的影响因素建立三轴加速度计误差模型[8]：

图1 姿态解算流程Figure 1 Attitude calculation process

(1)

(2)

其中:Ax、Ay、Az为三轴加速度计输出原始值，Ax1、Ay1、Az1为三轴加速度计进行误差补偿后输出值，A_SCx、A_SCy、A_SCz为三轴加速度计的三轴比例系数，A_Kyx、A_Kzx、A_Kxy、A_Kzy、A_Kxz、A_Kyz为耦合因数，A_OSx、A_OSy、A_OSz为零位偏移.

对于三轴加速度计的误差不稳定性，采用静态六位置法对比例系数、安装误差和零位偏移进行标定，借助高精度转台进行测试，利用最小二乘法对六位置法测试数据进行最小误差估计得出12个误差系数[9].将式(2)用Y=WX代替，矩阵X由12个待测系数组成，矩阵W为三轴加速度计原始值，矩阵Y为已知的重力加速度值.

位置1，转台设备Z轴向下，设定此时[Ax1Ay1Az1]=[0 0 1]，在该位置采集n1个原始加速度值[AxAyAz]，此时

(3)

其中:矩阵Y1每一行元素为[0 0 1]，w1为原始加速度值.

位置2，转台设备Z轴向下，设定此时[Ax1Ay1Az1]=[0 0 -1]，在该位置采集n2个原始加速度值[AxAyAz]，此时

(4)

其中:矩阵Y2每一行元素为[0 0 -1]，w2为原始加速度值.

位置3，转台设备Z轴向下，设定此时[Ax1Ay1Az1]=[0 1 0]，在该位置采集n3个原始加速度值[AxAyAz]，此时

(5)

其中:矩阵Y3每一行元素为[0 1 0]，w3为原始加速度值.

以此类推，采集位置4、位置5、位置6时的数据.

将上述数据进行整理，令n=n1+n2+n3+n4+n5+n6，得

Yn×3=wn×4X4×3

(6)

(7)

利用最小二乘法可得:

X4×3=[WTW]-1WTY

(8)

1.2 改进欧拉角法姿态解算

设导航坐标系为onxnynzn，人体坐标系为obxbybzb，空间的关系如下：

(9)

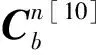
(10)

当静止或者匀速运动时，用加速度信号对姿态角进行估计[11]，由已知加速度重力分量得出X1、X2、X3.

(11)

欧拉角的更新为：

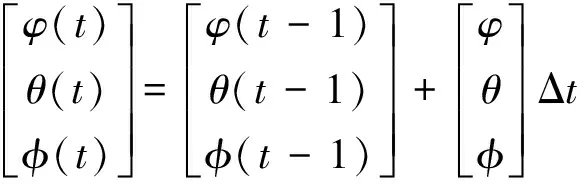
(12)

(13)

结合X1、X2、X3可以得出：

(14)

其中:ωx、ωy、ωz为各轴的角速度，Δt为采样时间.

1.2.1 滤波阶段KF1，倾斜角滤波

倾斜角滤波阶段使用的是加速度信号和角速度信号，倾斜角和加速度信号是线性关系，采用标准卡尔曼滤波器，滤波过程如下[12]：

(15)

其中

(16)

误差系数矩阵为：

(17)

更新数据为：

(18)

其中

(19)

Hk=-gI3×3，Qk-1为三轴陀螺仪输出的噪声协方差矩阵，Rk-1为三轴加速计测量的噪声协方差矩阵，测量值yk为加速度测量值.

1.2.2 滤波阶段KF2，航向角滤波

航向角与三轴磁力计信号是非线性关系，采用扩展卡尔曼滤波[13]，分为奇异值时滤波和非奇异值时滤波两种情况.

对非奇异值时， 航向角认定为标量， 由航向角的微分方程的误差协方差矩阵pk,2的更新矩阵为：

(20)

观察方程为：

yk=h(X1,X2,X3,φ)=Hb

(21)

误差协方差矩阵为：

(22)

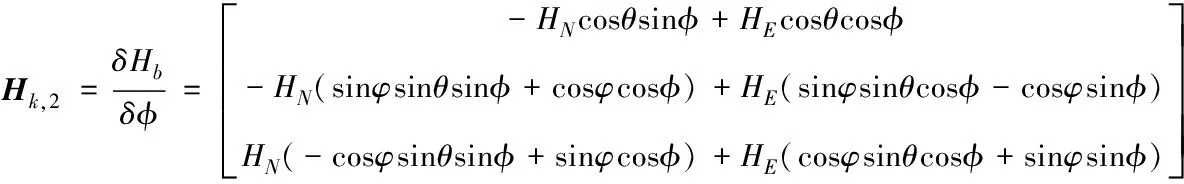
(23)

其中:HN、HE、HD为三轴磁力计各轴的磁场强度.

对于出现奇异值时，滤波器模式为奇异值模式.俯仰角接近90°时，状态方程为φ-λ，俯仰角接近-90°时，状态方程为φ+λ.状态方程使用方向余弦更新矩阵[14]，φ-λ或φ+λ的误差协方差矩阵为Pk,3，当俯仰角不是奇异值时，Pk,3为：

Pk,3=Pf+Pφ≈Pk(2,2)+Pk,2

(24)

由于X2的误差很小，所以X2的误差被认为是横滚角误差，在正常情况下Pk,3每次迭代过程中必须用上式初始化.

用方向余弦矩阵用来更新误差协方差为：

(25)

通过引入元素φ+λ和φ-λ解决[15]，此时，微分方程为：

(26)

(27)

使用矩阵G,更新误差协方差为：

(28)

当俯仰角接近90°时，观察方程为：

(29)

当俯仰角接近-90°时，观察方程为：

(30)

2 实验及结果分析

如图2所示，实验设备为三轴惯性转台和MEMS惯性传感器，测试时将传感器固定在转台上.

图2 惯性转台和惯性传感器Figure 2 Inertial turntable and inertial sensor

2.1 三轴加速度计标定实验

将三轴加速度计在上述的位置1、位置2、位置3、位置4、位置5、位置6的进行测试，为了消除实验过程中可能存在的操作失误等因素，对三轴加速计静态原始数据多次采集，得到由加速度原始数据组成的W和已知重力加速度向量Y，再结合式(5)利用最小二乘法求得12个标定系数组成的矩阵X4×3.采集静态原始数据如图3、4所示，并求出12个标定参数的均值和标准差.实验结果表明，求得的误差参数的标准差非常小，可以很好的对三轴加速度计的安装误差、比例系数和安装误差进行补偿.

图3 三轴加速度计各轴的零偏和比例系数Figure 3 Zero bias and proportionality coefficients of three axis accelerometer

图4 三轴加速度计各轴的耦合系数Figure 4 Coupling coefficient of each axis of three axis accelerometer

2.2 MEMS惯性传感器动态实验

将惯性转台进行随意转动、奇异点位置转动和外界磁场变化时转动，输出改进的欧拉角法和四元数法的两种姿态角，其结果如图5～7所示，在一般转动和奇异点转动的情况下改进的欧拉角与四元数输出结果相近，避免的传统的欧拉角法奇异点问题，在出现外界磁场变化时，改进欧拉角法比四元数法更加稳定，误差更小.

图5 随意转动输出欧拉角Figure 5 Rotate the output Euler Angle freely

图6 奇异点转动输出欧拉角Figure 6 Singular point rotation output Euler Angle

图7 外界磁场突变输出欧拉角Figure 7 External magnetic field mutation output euler Angle

3 结 语

经过三轴加速度计的标定实验和MEMS惯性传感器的动态实验得知，基于最小二乘法确定误差参数的标准差非常小，对三轴加速计标定补偿效果好；基于对欧拉角奇异值问题改进后，使得俯仰角在正负90°时姿态角不受影响；基于欧拉角法对倾斜角和航向角分开求解特点，大大减小磁场变化对姿态角的干扰，比四元数法在性能上更加优越，得到的姿态角精度高且稳定性好.因此，在人体姿态捕捉时，运用该方法可以获得高精度的姿态角.