数控机床磁流体润滑涂层齿轮摩擦性能分析*
2021-12-18崔传辉王优强
赵 辉 崔传辉 王优强
(①青岛理工大学机械与汽车工程学院, 山东 青岛 266520;②聊城大学东昌学院,山东 聊城 252000)
数控机床齿轮是机床传动系统的重要组成部分,其结构紧密、传动效率高、传动平稳,寿命长和可靠性高是其设计追求的目标。近年来,表面涂层技术发展迅速[1],涂层可以显著提高机械副表面的摩擦学性能。齿轮涂层因具有硬度高、耐磨性好和耐腐蚀等优点,在齿轮上应用可大幅提高齿轮接触疲劳寿命和抗胶合能力,有效延长齿轮使用寿命。
随着弹流润滑理论和混合润滑理论的发展,对无涂层和涂层齿轮副的摩擦学性能进行了广泛的研究。Liu H J等人[2]研究了齿面粗糙度、非牛顿流体行为、齿动载荷对轮齿摩擦学性能的影响。Li S等人[3]基于混合润滑模型,研究了齿轮的疲劳和胶合行为。Liu H J等[4]研究了涂层直齿轮瞬态热弹流响应。Habchi W[5]对点接触的涂层系统的弹流问题进行了分析。Ziegltrum A等[6]通过计算得到了线接触涂层齿轮副的减摩机理。然而,磁流体润滑涂层齿轮副的弹流润滑问题研究未见有报道。
磁流体[7]被定义成一种多功能的流体,其组成主要包括磁性纳米微粒、载液和表面活性剂。赵晶晶等[8]对不同磁流体润滑的渐开线直齿圆柱齿轮进行了理论分析。青岛理工大学的衣雪娟[9]应用多重网格技术,综合考虑齿轮啮合点的曲率半径变化、卷吸速度变化、单双齿引起的载荷变化,对齿轮的一对轮齿从啮入到啮出的全过程进行了研究,得到了齿轮时变弹流润滑的完全数值解。本论文基于该理论方法,进一步分析磁流体润滑条件下涂层对齿轮润滑性能的影响。
1 几何模型
由参考文献[9]可知,图1为直齿轮传动的几何参数示意图,为了便于分析计算,采用笛卡尔直角坐标系。

2 基本方程
2.1 Reynolds方程
润滑剂为Ree-Eyring流体,是非牛顿流体,非稳态线接触的Reynolds方程写为
(1)
式中:p为磁流体润滑膜压力;h为磁流体润滑膜厚度;其他参数含义和方程边界条件可参考文献[9]。
2.2 膜厚方程


(2)
式中:h00为未知的刚体中心膜厚,E′为两接触表面的综合弹性模量。
2.3 黏度方程
采用Roelands公式[10]:
η=η0exp{(lnη0+9.67)×
[(1+5.1×10-9p)Z0-1]}
(3)
2.4 密度方程
采用Dowson-Higginson公式[10]:
ρ=ρ0[1+(0.6×10-9p)/(1+1.7×10-9p)]
(4)
2.5 本构方程
润滑油为Ree-Eyring非牛顿流体的本构方程为:
(5)
数值计算中,啮合点的载荷使用的是齿轮传动中一对轮齿上的实际载荷谱简化模型[9]。齿轮数值分析方法和齿轮润滑油参数可以参考文献[11],此处不再叙述。
由文献[12]可知,涂层弹流模型与非涂层弹流模型的主要区别在于弹性的影响系数。涂层和基底的材料特性分别用下标“c”和“s”表示。
相关的公式推导可以参考文献[4],本文中取Ec=6Es,涂层厚度为160 μm,与文献[4]中一致。
3 结果分析
由文献[8]可知,本课题组成员分析了不同磁流体润滑对齿轮的影响,故选择二酯基磁流体,其黏度为0.075 Pas,密度为1.185 kg/m3。本文将主要分析该磁流体润滑条件下涂层的协同影响。
现在分3种情况对磁流体润滑渐开线直齿圆柱齿轮的摩擦学性能进行分析:第一种工况为两个齿轮均没有涂层;第二种工况为一个齿轮有涂层,另一个齿轮没有涂层;最后一种工况为两个齿轮均有涂层。
由图2可知,有涂层齿轮参与啮合与无涂层齿轮啮合的中心膜厚随啮合线的变化规律一致。沿着啮合线方向,在同一个啮合位置,有涂层齿轮参与啮合的中心油膜厚度,比没有涂层的啮合齿轮的中心膜厚要大。当参与啮合的两个齿轮均有涂层时,相同位置其中心膜厚最大。齿轮的涂层改善了啮合区的润滑工况。

由图3可知,有涂层齿轮参与啮合与无涂层齿轮啮合的最小膜厚随啮合线的变化规律一致。沿着啮合线方向,在同一个啮合位置,有涂层齿轮参与啮合的最小油膜厚度,比没有涂层的啮合齿轮的最小膜厚要大,这一点与中心膜厚变化规律一致。当参与啮合的2个齿轮均有涂层时,相同位置其最小膜厚最大,润滑工况最好。

由图4可知,有涂层齿轮参与啮合与无涂层齿轮啮合的中心压力随啮合线的变化规律一致。沿着啮合线方向,在同一个啮合位置,有涂层齿轮参与啮合的中心压力,比没有涂层的啮合齿轮的中心压力要小。当参与啮合的两个齿轮均有涂层时,相同位置其中心压力最小,对齿轮的应力破坏作用最小。

由图5可知,有涂层齿轮参与啮合与无涂层齿轮啮合的最大压力随啮合线的变化规律一致。沿着啮合线方向,在同一个啮合位置,有涂层齿轮参与啮合的最大压力,比没有涂层的啮合齿轮的最大压力要小,这一点与中心压力变化规律一致。当参与啮合的两个齿轮均有涂层时,相同位置其最大压力最小,避免较大集中应力对齿轮的负面作用。同时无涂层齿轮啮合初期最大压力变化出现波动,而有涂层齿轮相对稳定,对润滑有利。

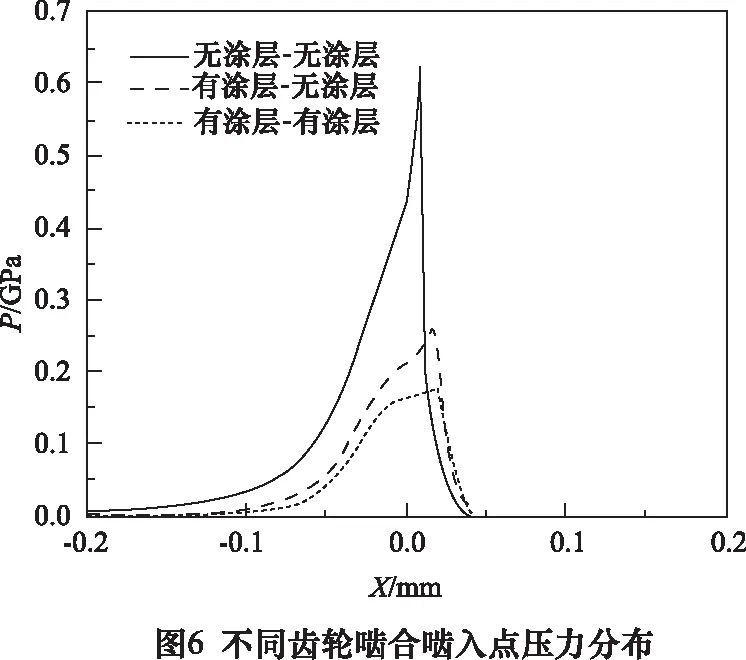
由图6可知,有涂层齿轮参与啮合与无涂层齿轮啮合的在啮入点的压力分布规律基本一致。有涂层齿轮参与啮合的第二压力峰更平缓,对润滑有利。
由图7可知,有带有涂层的齿轮参与啮合与无涂层齿轮啮合的在啮入点的膜厚分布规律基本一致。有涂层齿轮参与啮合的油膜厚度较大,对润滑有利。

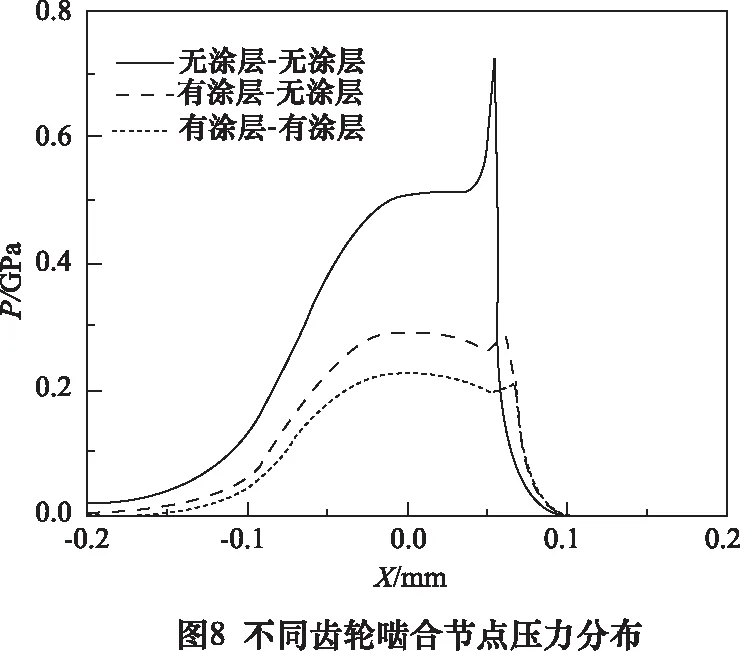
由图8可知,与啮入点类似,有带有涂层的齿轮参与啮合与无涂层齿轮啮合的在节点的压力分布规律基本一致。有涂层齿轮参与啮合的第二压力峰更平缓,在节点位置的压力分布更加接近赫兹压力分布,对润滑有利。
由图9可知,与啮入点类似,有带有涂层的齿轮参与啮合与无涂层齿轮啮合的在节点的膜厚分布规律基本一致。有涂层齿轮参与啮合的油膜厚度较大,对润滑有利。

由图10可知,与啮入点和节点类似,有带有涂层的齿轮参与啮合与无涂层齿轮啮合的在啮出点的压力分布规律基本一致,但第二压力峰消失。有涂层齿轮参与啮合的压力峰值更平缓,对润滑有利。

由图11可知,与啮入点和节点类似,有带有涂层的齿轮参与啮合与无涂层齿轮啮合的在啮出点点的膜厚分布规律基本一致。有涂层齿轮参与啮合的油膜厚度较大,对润滑有利。

4 结语
(1)对于磁流体润滑条件下渐开线直齿圆柱齿轮,沿着啮合线方向,有无涂层齿轮参与啮合,其压力膜厚变化规律一致。在相同啮合点位置,有涂层齿轮参与啮合的油膜厚度较大,对润滑有利。
(2)在啮合过程中的啮入点、节点和啮出点3个特殊位置,有涂层齿轮参与啮合的第二压力峰位置压力分布更加平缓,避免了较大应力集中对齿轮的破坏作用。
