多稳态夹芯金属压杆的滞后阻尼增强机制与被动减振性能

方 辉，靳汉文，孟祥剑，段利亚

(1. 中国海洋大学 工程学院 山东省海洋工程重点实验室，山东 青岛 266100；2. 齐鲁工业大学(山东省科学院) 海洋仪器仪表研究所，山东 青岛 266061)

波浪破碎于结构前产生瞬时强载，钢结构可抵抗砰击强载，但固有阻尼极低，砰击振动低衰减传播，是海工结构损伤的重要原因[1-5]。多类结构振动抑制方法中[6-7]，主动、混合控制方法具有较好效果[7-12]，但难以保障必需的能源供应；被动减振无需供能[13-15]，多采用黏性材料增强金属结构阻尼，根据阻尼和线性结构理论[16]，阻尼材料在结构中需达到较高比例，但阻尼材料极低的模量会降低结构整体刚度。由上可见，线性结构理论下高刚度与高阻尼设计间存在原理性矛盾。

基于多稳态转换可实现构件力—位移滞后特性[17]，Dong和Lakes[18]提出边界跳变压杆，初始状态下该类压杆边界为全接触压实的类固支状态，压缩载荷达到一定阈值后边界跳变为边缘接触的类简支状态，与此相对应，压杆稳态由轴压直杆、固支弯曲转换为简支弯曲，这一过程中压杆刚度循环变化使力—位移关系具有滞后特征；但是，稳态跳变过程中这类均匀直杆易出现局部塑性而破坏，同时，该构件稳态转换后变为低刚度会使变形突增而易于失稳。为达到有效承载，季树彬等[19]设计了一类偏心钢制压杆(图1(a))，有效控制了屈曲过程而消除局部塑性，进而引入协同弹簧以承担刚度下降产生的负载，实现了结构多稳态转换过程稳定承载，并给出稳定性和非线性振动的解析方法[20]，该类偏心全金属压杆耗散性能正比于屈曲阈值，设计中为提高耗散需增大构件截面或缩短长度，这会使轴压状态下构件刚度偏高，因此该类压杆轴压刚度和滞后阻尼性能的设计优化因稳定性原理而存在矛盾。

为提高多稳态压杆的可设计性，即保持适当刚度同时增强滞后阻尼，研究提出了一种多稳态夹芯金属支撑；采用有限元模拟，描述了该类压杆稳态随循环载荷转换规律和力—位移滞后关系，并与具有相同轴压刚度的全金属偏心压杆[20]进行对比；采用夹芯结构弹性理论和变边界结构稳定理论，与有限元模拟结果对比给出该类压杆滞后阻尼增强的机制；以该类压杆替换导管架斜撑，采用有限元方法模拟巨大瞬态作用下结构振动，并分析其衰减特性。

1 多稳态夹芯金属压杆

图1(a)为偏心钢制压杆示意[20]，该类结构具有可变边界，压缩载荷作用下，初始状态为轴压直杆，压杆上下端部与压板间为压实接触，随载荷增大，压杆变为局部弯曲，其端部与压板间保持压实接触，载荷进一步增大，该压杆变为整体弯曲，端部与压板间转变为边缘接触。图1(b)为研究提出的多稳态夹芯金属压杆，相对于偏心钢制压杆，新压杆主体(图1(b))为钢/聚合物/钢夹芯结构，图中T0、T1和T3均为钢材，T2所示为聚合物聚甲基丙烯酸甲酯(PMMA)，新压杆端部相对于夹芯体厚度增大且两侧非对称。图1(c)为夹芯压杆网格划分。图1(d)表示压杆与协同线弹簧并联，高刚度辅助支架(左侧两子图，远高于竖直状态压杆轴压刚度)使各组件协同作用；外载沿整体结构轴向拉伸时辅助支架中两部分沿轴向分离使压杆压缩，外载沿整体结构轴向压缩时辅助支架中两部分接近使压杆压缩，即拉压循环中夹芯压杆总处于受压状态。

1.1 有限元模拟

夹芯压杆几何参数列于表1，整体支撑结构所用材料[21]列于表2，其中T1和T3厚度对应部件为钢制，T2厚度对应聚合物，B为压杆宽度，辅助支撑结构为钢制。为使辅助支架刚度远大于夹芯压杆，其承载截面远大于夹芯压杆。有限元模拟采用ABAQUS的隐式算法[22]，压杆端部采用刚体建模，压杆端部与辅助支架间为面接触，切向为“hard”，法向为“rough”,摩擦系数为0.3；模型(图1(c))采用8节点减缩积分单元(C3D8R)，网格尺寸为0.005 mm，整个模型共20 652个单元。正弦载荷大小为2.4×106N(图2 (a))，作用于整体结构顶部，整体结构底部固支，并联弹簧(单根)刚度为8×107N/m。图2(b)为夹芯压杆端部轴向支反力(纵轴)与整体支撑结构顶部位移(横轴)关系曲线，其中，阶段1(曲线中点0～1)，支反力—位移为线性关系，压杆轴压竖直稳定且边界全接触压实(图2(c)左侧子图)；阶段2(曲线中点1～2)，支反力达到阈值(点2)，位移—支反力斜率很小，压杆转换为局部弯曲稳定且边界全接触压实(图2(c)中间子图)，由下一小节可知点2为类固支压杆屈曲载荷；阶段3(曲线中点2～3)，位移继续增加至阈值(点3)，支反力快速降低，即压杆出现负刚度，转换为整体弯曲稳定且边界为边缘支撑(图2(c)右侧子图)，由下一小节可知点3为压杆由全压实向边缘支撑边界转换的临界载荷；阶段4(曲线中点3～3′及点3′～4)，加载曲线由点3向点3′以线性发展，卸载曲线由点3′经点3向点4，初始阶段依线性关系，位移接近初始加载阶段(点0～1)，压杆刚度增大、跳变回轴压直杆且边界转换回全接触压实。夹芯压杆稳定状态随循环载荷依直杆—局部弯曲—整体弯曲—直杆循环变化，刚度随之改变使得支反力—位移形成滞后回环。考虑协同弹簧承载，整体支撑结构力(循环载荷)—位移(结构自由端)关系形成旗帜型滞后回环，如图2(a)所示。循环加载各组件始终处于弹性(图2(c))。考虑已有偏心金属压杆(图1(a))[20]，结构参数如表1，有限元模拟结果如图2(a)和2(b)所示：轴压刚度与夹芯压杆轴压刚度一致，夹芯压杆稳态转换阈值(点1和2)远大于偏心金属压杆(约为4倍)，新型夹芯压杆滞后回环面积远大于已有偏心金属压杆(约为12倍)，由下文解析计算可知夹芯结构可有效调节弯曲和轴压刚度的组合，能够实现适用刚度和增强阻尼的更优化设计。

图1 多稳态压杆示意Fig. 1 Schematic diagram of multiple steady-state pressure bars

表1 夹芯压杆几何参数Tab. 1 Geometrical parameters of bilayered column

表2 材料参数Tab. 2 Material parameters

图2 荷载、位移及应力云图Fig. 2 Load, displacement and stress nephogram

1.2 解析计算

考虑前述钢/聚合物/钢夹芯杆弯曲承载(图3)，图3中上下面板厚度分别为T1和T3，z0、z1、z2、z3为虚线对应z轴坐标值，T1为z0-z1，T3为z3-z2，芯材厚度T2以坐标值表示应为z1+z2。zi为夹芯杆表面及界面(图中以虚线标识)于坐标系x-z中的z轴坐标值。依文献[21]可知夹芯结构弯曲刚度为：

(1)

竖直轴压刚度为：

(2)

式中：i=0～4代表材料的分层编号；Ai、Ti、B分别为不同层面积、厚度和整体宽度。压杆轴压稳定时力—位移关系为：

F=Kau/2Le

(3)

图3 夹芯杆弯曲示意Fig. 3 Bending mode of sandwich column

压杆端部与辅助支架间初始为压实接触，加载中会跳变为边缘接触的类简支；对于变边界压杆弯曲问题，Timoshenko和Gere[23]给出了一类计算模型(图4)，端部等效为圆弧，载荷F作用偏移量为D=Reθ(θ值较小)，圆弧半径则随边界变化而改变。微弯偏心压杆的弯矩—挠度关系为：

(4)

其中，δ=z(Le)为挠度，并进行无量纲化：

z″″+λ2z″=0

(5)

(6)

图4 压实—边缘支撑变边界压杆弯曲模型Fig. 4 The analytic model of bilayered column

由式(5) 可得：

z(ε)=C1sin(λε)+C2cos(λε)+C3ε+C4

(7)

式中：C1=C3=0，C2=-C4。因此式(7)可表示为：

λsin(λπ/2)+(Le/r)cos(λπ/2)=0

(8)

压杆边界压实，Re/Le→∞，屈曲载荷为：

(9)

屈曲载荷即为图2(b)中点2。压杆局部弯曲后变形为：

z(ε)=C4[1-cos(2ε)]

(10)

考虑压杆大变形，弯矩—挠度关系为：

(11)

级数展开并略去高阶项，以伽辽金法得：

(12)

其中，λ=λ0+μλ1，可得：

(13)

压杆边界由压实转换为边缘接触(图2(c)中右侧子图)，μ=2Le/(πr)数值较小，以上式(13)中λ，F和C4可采用级数展开并取一阶，λ=λ0+μλ1，F=F0+μF1，C4=C40+μC41，可得：

z(ε)=C40[1-cos(λ0ε)]+μ[C41-C41cos(λ0ε)+C40λ1sin(λ0ε)]

(14)

载荷F移动距离为：

(15)

边界转换时D=T/2，代入式(13)得：

(16)

式中：Fcr2为第二次稳态转换阈值。Fcr1达到Fcr2这一过程中，杆件两端相对位移为：

(17)

其中，u12即为图2(b)中点2至3的横轴坐标差。压杆转换为边缘接触，进入类简支状态，屈曲阈值为：

(18)

其中，Fpin=1/4Fcr1，K*为等效刚度。因压杆端部与主体细长部分截面差异较大，采用等效方法取有效杆长约为760 mm，解析计算所得Fcr1，Fcr2，Fpin和μ12与有限元模拟结果近似。

1.3 刚度—阻尼综合性能对比

材料阻尼理论[24]中，以模量E*和损耗因子tanφ分别表征刚度和阻尼，并以两者乘积表征刚度—阻尼综合性能。图5给出多类材料刚度—阻尼特征，例如：金属高刚度、低耗散(<10-4)，处于图5左上角，橡胶高损耗、低刚度处于图5右下角。Lakes[24]以|E*|tanφ=0.6 GPa为刚度—阻尼综合性能的参考指标，即高刚度、高阻尼。对于新型构件，采用李萨如法[24]，等效刚度为滞后回环对角等分线斜率，以滞后回环外接矩形范围内已知滞后椭圆(取tanφ=1)面积的倍数，得到等效损耗因子。图5中五角星(|E*|tanφ=56 GPa)为图1(b)中所示夹芯压杆等效刚度(E*≈ 95 GPa)和等效阻尼(tanφ≈ 0.59)，新构件具有高刚度和高阻尼。

图5 材料刚度—阻尼特征Fig. 5 Stiffness-damping of material

2 砰击导管架被动减振模拟

研究以砰击试验中5层导管架平台(图6)为模拟对象[24-25]，层高10 m，立柱内外径为1.2 m和1.1 m；横撑内外径为0.56 m和0.50 m，长度为10 m；斜撑横截面积为0.03 m2；各构件均采用Q235钢(弹性模量210 GPa，泊松比0.3，屈服强度235 MPa)；结构自重(5.63×105kg)和上部组块(2.44×106kg)质量分布于各相邻节点；立柱底端固定。为直接对比新型滞回构件的耗能性能，研究中所有导管架模型都未考虑结构阻尼。传统弹塑性设置建立导管架模型，标记为模型1，桩腿和横撑均采用B31单元，斜撑采用T3D2单元，载荷采用砰击试验[25]所得结果，幅值为2.4×106N(图7(a))，砰击施加于导管架第4层(图6)，采用ABAQUS的隐式动力算法，图7(b)为导管架顶部节点位移时程曲线，砰击后模型1自由振动的周期为1.78 s，与特征值法所得模型一阶周期相同。

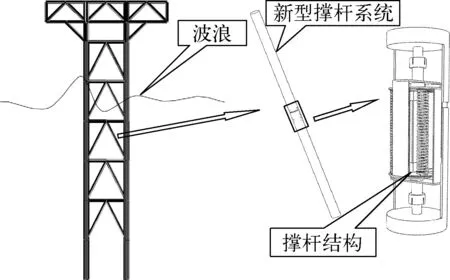
图6 导管架平台及嵌入夹芯压杆结构的斜撑Fig. 6 Jacket platform and diagonal brace with bilayered column

图7 荷载及振动衰减曲线Fig. 7 Load and vibration attenuation curves

为了抑制砰击作用下导管架结构振动，将全部斜撑替换为新型滞后性支撑构件，该支撑主体为图1(d)所示辅助支架所装配多稳态夹芯压杆和协同线性弹簧的并联滞后结构，考虑工程应用，该支撑构件由滞后构件、连接件和封装件组成(图6)。基于模型1计算结果和前述理论方法(1.2节)，对夹芯结构和支撑构件进行优化设计，优化所得压杆结构参数见表1。对于导管架模拟，为提高计算效率和收敛性，滞后斜撑上以T3D2单元建模的直杆表示，其中以ABAQUS的用户定义子程序赋予单元力—位移滞后关系，该模型其它设置(例如边界、砰击等)与模型1相同,以上引入滞后斜撑导管架模型记为模型2。为了直接评价新型撑杆耗能效应，以上两个模型中未考虑结构自有阻尼。模型2的位移响应时程曲线(图7(b))显示自由振动周期为1.75 s，说明模型1和2刚度十分接近，模型2振动初始幅值与模型1接近，但衰减速率远大于模型1，模型2中各单元一直处于弹性。作为对比，考虑已有偏心压杆[20]，其几何和物理参数见表1和表2，以其替换模型2中夹芯压杆，该导管架模型标记为模型3，其它设置与模型2相同。模型3振动响应时程见图7(b)，自由振动频率和初始幅值与模型2相同，但是振动衰减率低于模型2。由文献[20]可知提高偏心压杆耗散效率，需多压杆串联，这不利于刚度设计，还会增加成本。如模拟中考虑结构自有阻尼，采用瑞利阻尼法，一阶模态、阻尼比1%，模型1振动衰减加速，模型2瞬态振动衰减仍比模型1更快，因篇幅限制，相关计算结果未列入文中。

对于更一般的设计过程，如图8所示，在实际结构中，根据承载要求确定结构刚度，进行新型撑杆结构设计：首先，对照导管架整体尺寸确定新型承载外部圆筒尺寸；然后，总刚度分配给压杆和弹簧；最后，以前述刚度确定拉压框架的刚度。初步设计后，进行有限元模拟验证，以及关键承载性能评估，包括屈曲荷载峰值、滞后回环大小、减振性能，在此基础上优化建模细节和参数，在保证刚度的基础上，尽量扩大滞后回环面积，从而提高减振性能，最终达到高刚度、高耗散的结构优化设计目的。

图8 结构设计流程Fig. 8 flow chart of structural design

3 结 语

为实现构件高刚度并增强其阻尼，研究设计一种多稳态夹芯金属压杆；有限元模拟循环载荷作用于以夹芯压杆为主体的新型支撑构件，夹芯压杆稳态及对应刚度依序变化使力—位移间产生滞后关系，相对于具有相同初始高刚度的偏心金属压杆[20]，新构件耗散性能提高了约12倍；基于层合结构和变边界压杆稳定性理论进行解析计算，结果与有限元模拟一致，夹芯结构有效调节弯曲和轴压刚度的组合，实现了适用刚度和增强阻尼的更优化设计；以砰击导管架为例，有限元模拟中新型滞后支撑结构有效增强了结构阻尼，使振幅幅值快速衰减，相对于传统设计更好保障了结构安全。