基于力流分析的铁路承台三维拉压杆模型研究
2022-05-19王雨权廖立坚苏伟刘祥君宋威李林安
王雨权,廖立坚,苏伟,刘祥君,宋威,李林安
(1.中国铁路设计集团有限公司 土建工程设计研究院,天津 300308;2.天津大学 机械工程学院,天津 300350)
0 引言
铁路承台联结桥墩与桩基,受力复杂。长期以来,铁路设计规范中,没有关于承台设计配筋的理论和计算方法。在实际设计中,采用的是45°扩散角控制并结合建筑规范的“深梁受弯理论”[1-3]或套用公路的“撑杆-系杆理论”[4]来设计。
针对承台结构,国内外开展过不少研究,东南大学郭宏磊等[5]对4个六桩承台进行了试验研究;华南理工大学季静等[6]对二、三、四及六桩承台进行了试验研究;Perry等[7]在1990年进行了6个承台的模型试验,Rafael Souza等[8]则构建了一种可适应的拉压杆模型。
铁路承台与建筑基础或公路承台的结构形状、载荷区别较大,套用其他行业规范缺乏依据,也与框构桥等结构的受弯形式有所不同[9]。另外,从铁路本身行业纵向比较发现,过去配筋率较低的承台在运行几十年后,仍能满足使用,这种现象需足够引起铁路设计者反思。
在以往研究成果的基础上[10],在此进一步阐述依托石济高铁承台的研究成果。利用Ansys分别对最常用的8种类型承台进行力流分析,研究承台内部的受力机理,并基于受力分析模型,建立起一种简单实用的适用于铁路承台结构特点的三维拉压杆模型,该模型经检算,能满足模拟承台内部受力特点的精度要求,计算得到的配筋数量和钢筋布置形式满足承台所受载荷要求。
1 铁路承台力流分析
石济高铁承台中,桩径为1.00、1.25、1.50 m的承台最常用,选取8个使用频率最高的承台结构及配套桥墩和桩基,利用Ansys建立有限元分析模型。
计算模型的结构尺寸见表1。从表中可知,对于承台尺寸在8根1.25 m以上结构设计有加台。桩基的布置形式则可分为梅花式和行列式2种(见图1)。
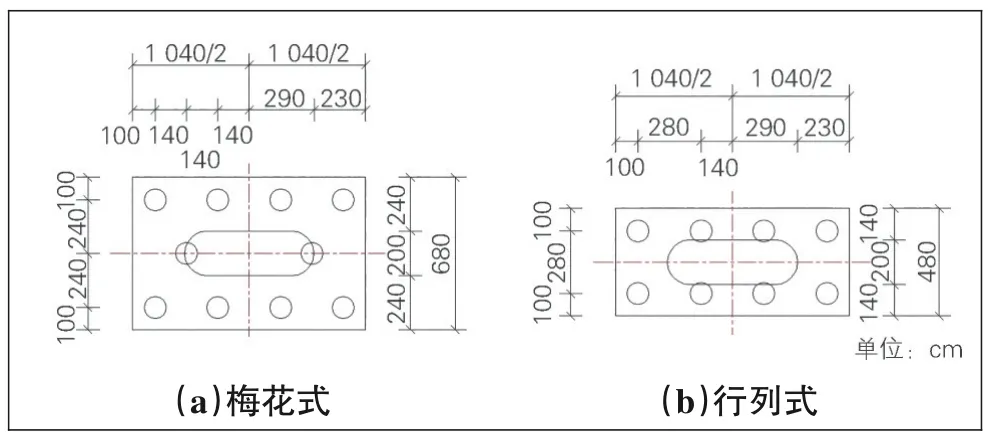
图1 桩基布置示意图
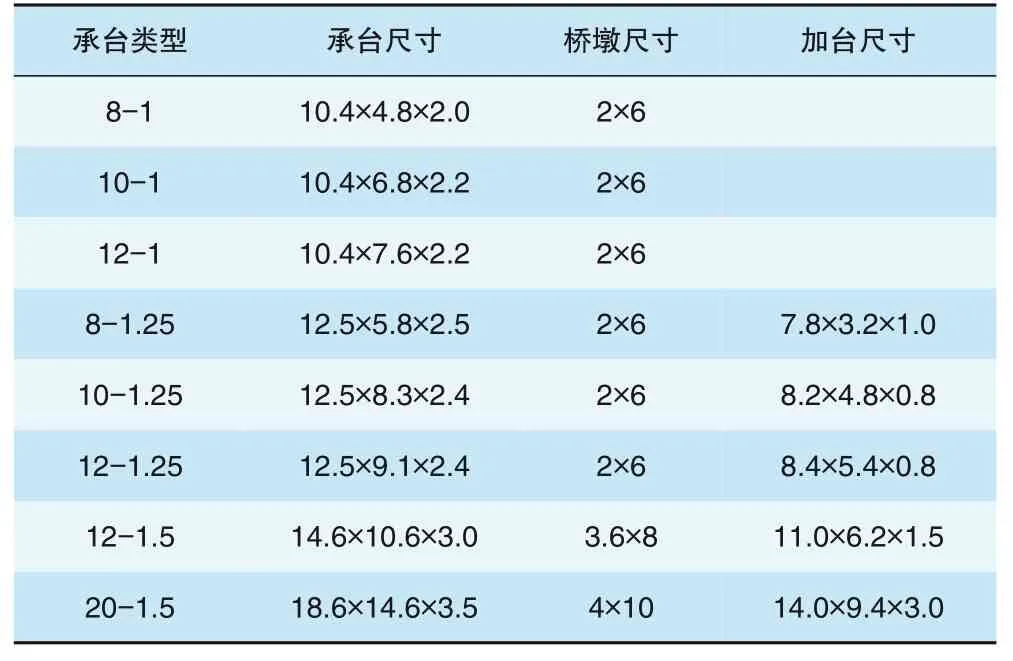
表1 有限元计算采用的石济高铁桥梁承台设计参数 m
铁路设计中,常规的桩基反力控制值分别为:1.00 m桩径4 000 kN,1.25 m桩径6 000 kN,1.50 m桩径8 000 kN。因此,在Ansys计算过程中,桩基反力控制值按如上取值加载,桥墩固结。8个计算模型对应的第三主应力图见图2。
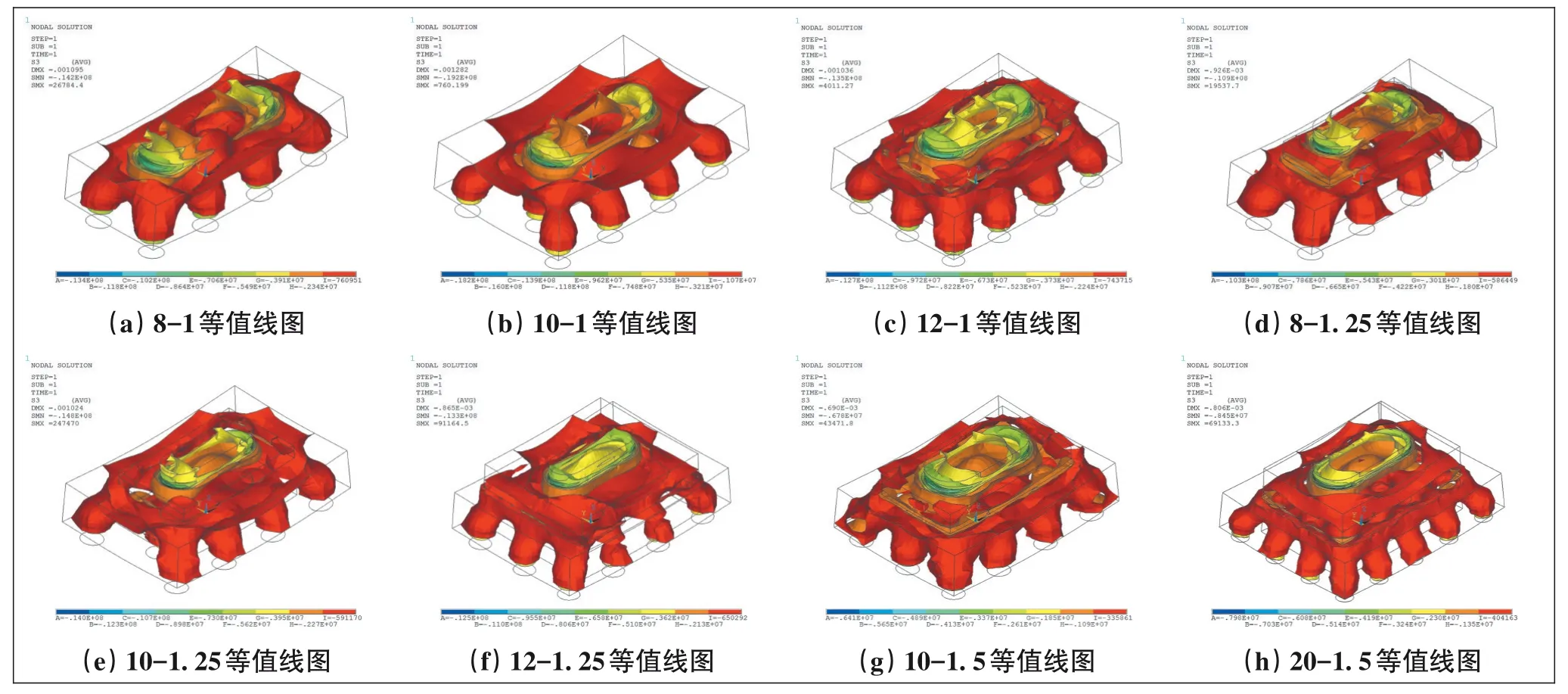
图2 8个计算模型第三主应力图
第三主应力代表受压,从图2的计算结果看,承台内部在载荷作用下能形成3个受力特点各异的区域,分别是局部受压区、压杆区域、受拉区域。其中各模型的压杆之上区域受力复杂,为局部受压区或称应力扰动区,压杆区下部桩之间区域则形成受拉区域。局部受压区,压杆及拉杆的受力分布示意见图3。
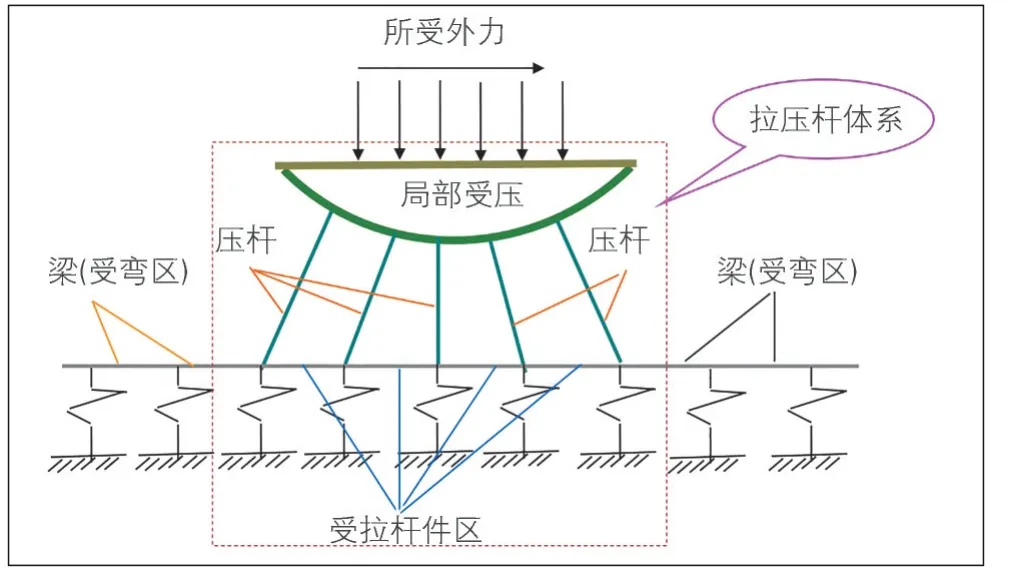
图3 承台简化受力模型
局部受压区与桥墩接触,大小与桥墩尺寸关联,形态也与墩形类似,因为计算模型的桥墩为圆端型桥墩,导致局部受压区形态类似于椭球,高度方向约为承台总高度的0.4~0.6倍。
在局部受压区与桩基之间,形成了明显的压杆。压杆的截面形状与桩基础有关,从Ansys的应力结果图估算,直径约为桩直径的1.2~1.5倍。受拉区位于承台底部的桩与桩之间,拉应力在承台底部中间位置最大,距离跨中越远拉应力越小。
压杆区域和受拉区域共同构成了空间三维拉压杆结构。依据此分析结果,即可建立能模拟承台受力特征的既简单又适用的力学模型。
2 三维拉压杆模型建立过程分析
从上述8个承台模型的受力分析可以看出,铁路承台存在明显的局部受压区(应力扰动区),导致承台截面的应力分布呈现出非线性特征,该区域的受力特点已不满足平截面假定,因此承台的受力特点与受弯构件是截然不同的。承台底部存在受拉区域,需要配置合理的钢筋才能平衡。局部受压区高度较大,可视为刚体,配筋计算不予考虑,受压区混凝土则构成了压杆体系,与钢筋构成了一个三维的拉压杆体系。
根据拉压杆研究相关理论,三维拉压杆模型的构形,应满足受力平衡和正确反映混凝土结构内部力流传递特征。在建立简化模型的过程中,拉杆和压杆的轴线应尽量与应力迹线重合,其中的压杆角度与根据应力合力计算得到的斜压杆角度相差不应超过15°。
为探求最适合于铁路承台简化计算的三维拉压杆模型,依据受力特点,遵循应力迹线法原则,建立几种类型的空间拉压杆模型,并对每种模型的拉压杆参数不断优化。三维拉压杆模型与实体计算模型结果相近的,即为得到的合理计算模型。
以石济高铁8根1 m桩径承台为例,展示三维拉压杆模型的建立过程,设该承台的高度为h,桩基直径为D。
模型1:模型共2层计8个节点,上层4个节点位于桥墩所围的2 m×6 m的矩形角点上,下层4个节点位于桩基中心位置,压杆高0.4h,拉压杆直径1.2D,基顶作用支反力4 000 kN(见图4),模型内力结果见图5。
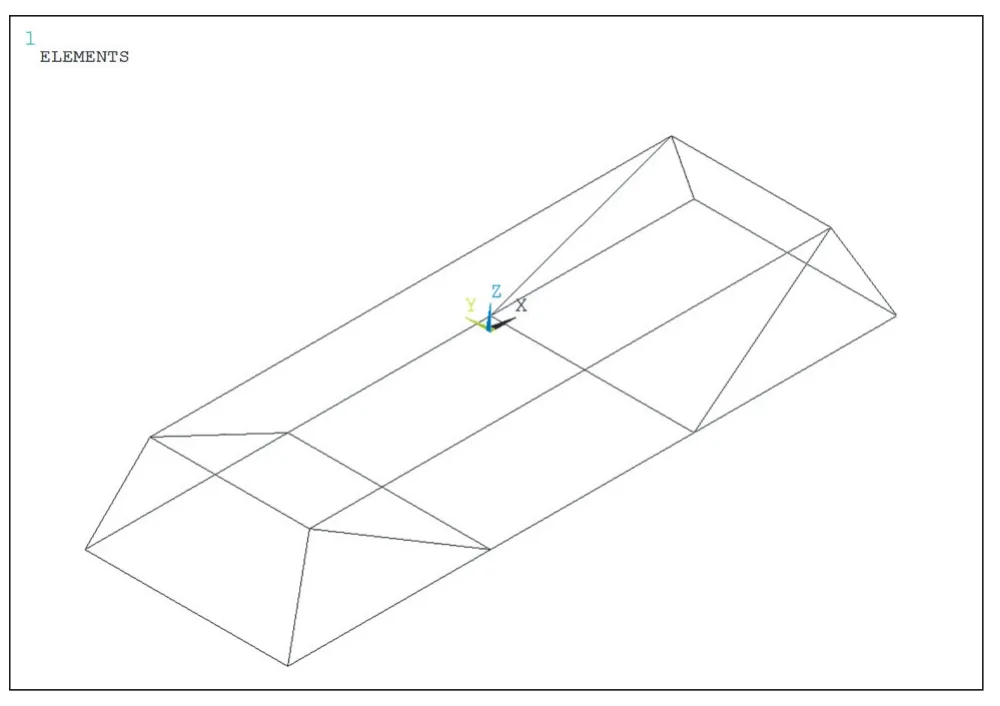
图4 模型1三维拉压杆示意图
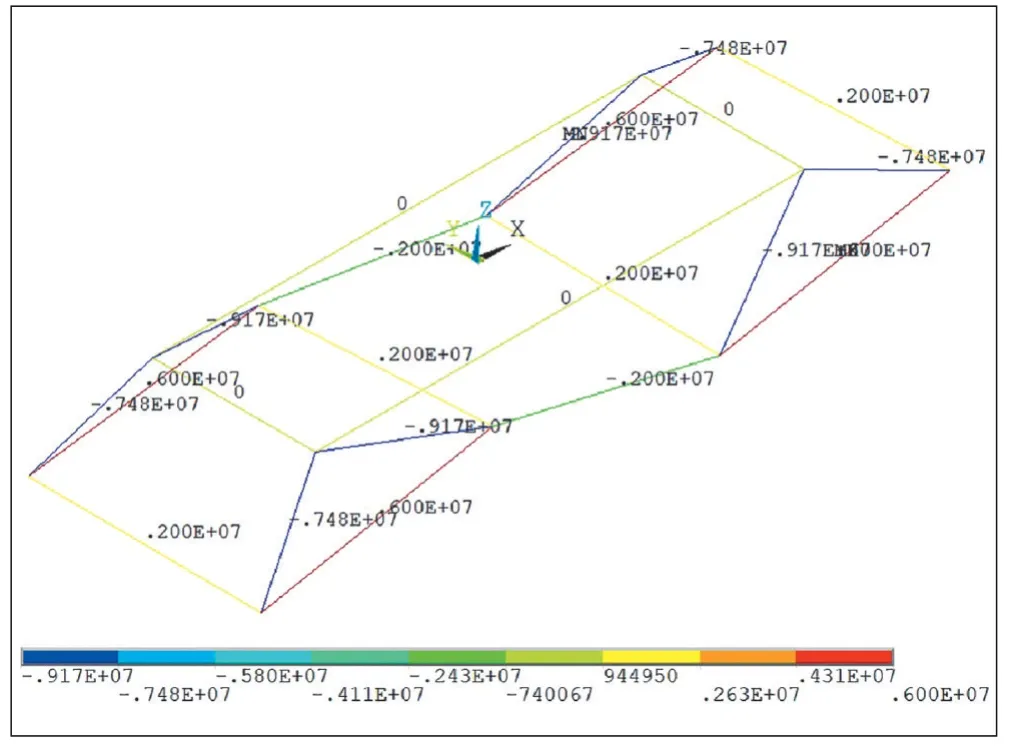
图5 模型1内力结果
图5为模型1的计算结果,可以看出,承台内部8根压杆受压明显(蓝色杆件);桩与桩之间的杆件为受拉杆件。压杆最小轴力为-9.17×106N,拉杆最大轴力为6×106N,但底面拉杆出现局部受压情况,经与实体模型结果对比,模型1不能很好地模拟承台受力特点。
模型2:在模型1的基础上,将压杆高度修改为0.45h,压杆中最小轴力为-8.35×106N,拉杆中最大轴力为5.33×106N,中间拉杆仍出现局部受压的不合理现象。
模型3:将压杆高度修改为0.5h,此时压杆最小轴力为-7.71×106N,拉杆最大轴力为4.8×106N,中间拉杆仍出现局部受压杆件的不合理现象。
上述3个计算模型表明,仅修改压杆高度不能得到理想状况,遂尝试修改拉压杆直径。
模型4:压杆高度为0.4h,拉压杆直径为1.4D。此时压杆最小轴力为-9.17×106N,拉杆最大轴力为6×106N,中间拉杆仍出现局部受压的不合理现象。
模型5:分析模型1—模型4,之所以拉杆会出现局部受压现象,原因可能是上下2层节点之间的压杆共用了节点。从这一思路出发,拟将压杆节点分开,考虑到铁路承台所接触的桥墩尺寸较大,将上层节点调整设置在桥墩尺寸的1.1倍尺寸上(见图6)。
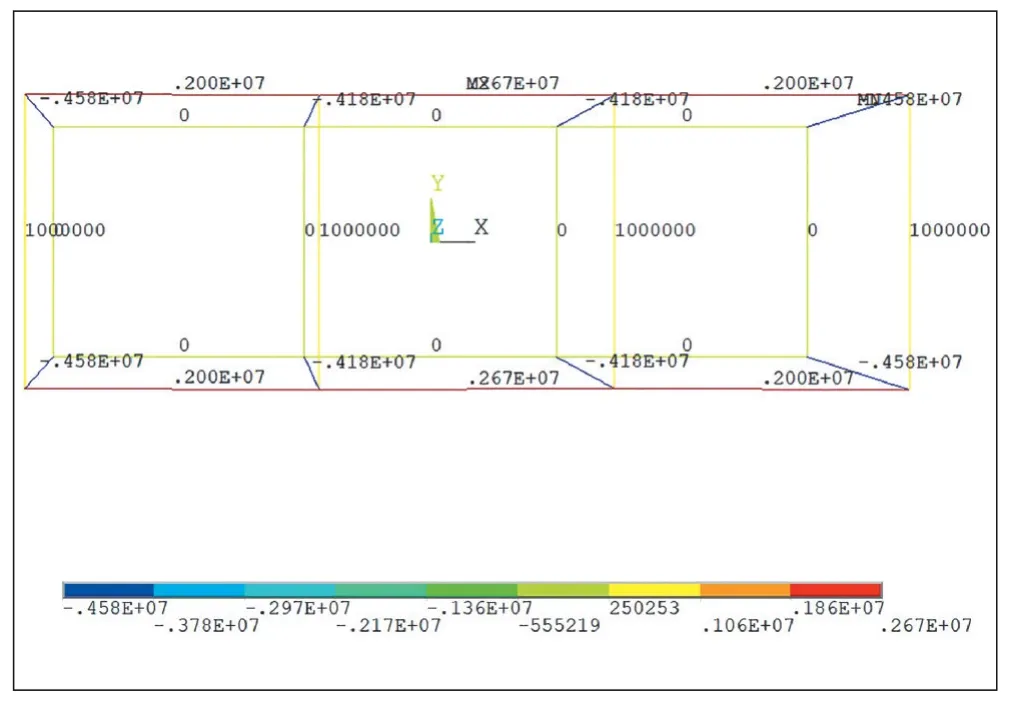
图6 模型5及其内力计算结果
压杆节点位置调整后,模型的受力与变形更加合理。考虑到压杆节点仍然要延伸到局部受压区,将压杆高度调整为0.6h,拉压杆截面直径为1.2D,在桩基反力4 000 kN作用下,压杆中最小轴力为-4.58×106N,横桥向拉杆最大轴力为2.67×106N,纵桥向方向最大轴力为1×106N,结果与三维实体模型相符。
三维实体模型的压杆平均压应力为-3.93 MPa,压杆直径约为1.2倍桩径,压杆最大轴力为-4.44×106N。
将上述5个模型进行汇总,并与实体模型对比(见图2),可以清楚地看到,对于模型1—模型4,由于压杆共用节点,轴力与三维模型结果相差较大,模型5将压杆节点分开,得到的计算结果与三维实体模型相差较小,仅为3.20%。
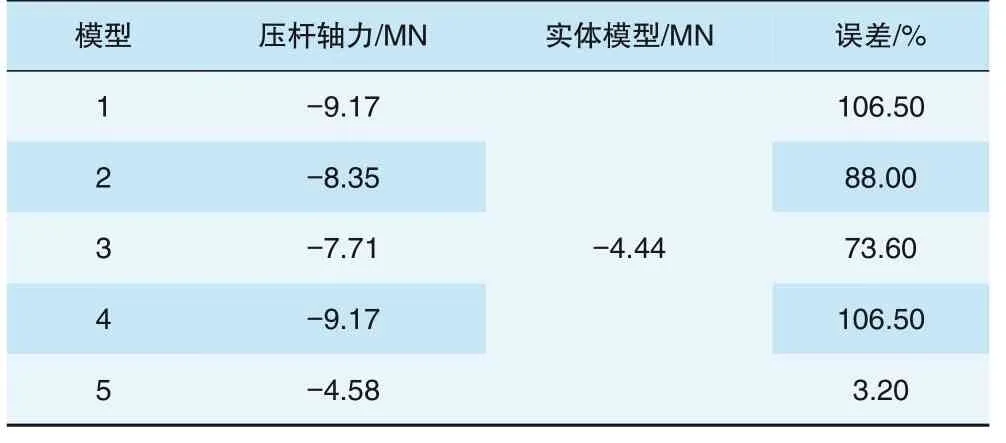
表2 各种简化模型轴力计算结果对比
3 三维拉压杆模型规律总结
上文详细列出了8根1 m桩径三维拉压杆模型的简化过程,其他7个承台也可采用类似方法得到各自的三维拉压杆模型。
经过对这8个承台三维拉压杆模型的分析,可以按照桩基布置形式分成2种模型形式:如8根1 m桩基承台的行列式布置形式和10根1 m桩基承台的梅花布置形式,2种模型布置示意分别见图7、图8。
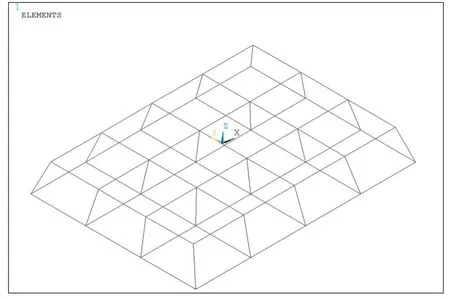
图7 承台行列式三维拉压杆模型示意图
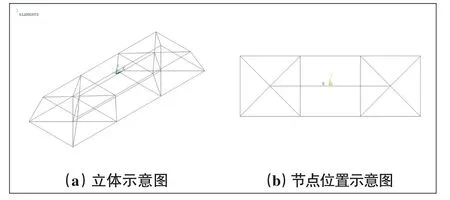
图8 承台梅花形三维拉压杆模型示意图
三维拉压杆模型尺寸按下列原则取值:
(1)压杆高度为承台高度的0.6倍。
(2)局部受压区简化为矩形,面积大于桥墩面积。对于无加台的承台,面积为桥墩面积的1.2倍;对于有加台的承台,面积为加台面积的1.1倍。
(3)压杆节点分开布置,不共用节点,数量与桩数等同,节点等间距。
(4)对于行列式承台,分别将承台横向和纵向相邻两桩节点相连,每个桩只与相邻桩形成拉杆。
(5)对于梅花布置承台,边桩按照矩形桩的连接方法形成拉杆,但中间呈梅花形的桩分别与相邻的边桩连成斜向拉杆,同时两梅花桩之间形成纵向拉杆。
4 三维拉压杆模型验证与应用
三维拉压杆模型计算的内力与实体模型计算结果非常接近,可以很方便地用三维拉压杆模型代替实体模型。
提取拉杆的内力用于配筋计算,钢筋数量可依据允许应力法按照式(1)计算:

式中:N为根据三维拉压杆模型计算得到的拉杆轴力;n为需要配置的钢筋数量;[σs]为钢筋容许应力;As为单根钢筋截面积。
计算得到的钢筋均匀配置在以桩基为中心、直径为桩径的1.2倍范围内。
为验证通过上述三维拉压杆模型计算得到的钢筋是否能满足承台受力要求,利用Ansys将用式(1)计算得到的钢筋配置入承台,进行承台钢筋混凝土三维实体模型的非线性计算。混凝土采用solid 65单元模拟,配置的钢筋采用link 8单元模拟,计算过程中混凝土采用MISO强化准则及William-Warnker破坏准则。以8根1 m桩径的承台为例,混凝土采用C35,其容许抗压应力为11.80 MPa,容许主拉应力为2.25 MPa,张开裂缝的剪力传递系数为0.50,闭合裂缝的剪力传递系数为0.95,弹性模量为3E4 MPa,泊松比为0.2,拉应力释放系数采用0.6。
由于实体钢筋混凝土非线性计算量巨大,可利用承台结构的对称性建立1/4模型(见图9)。
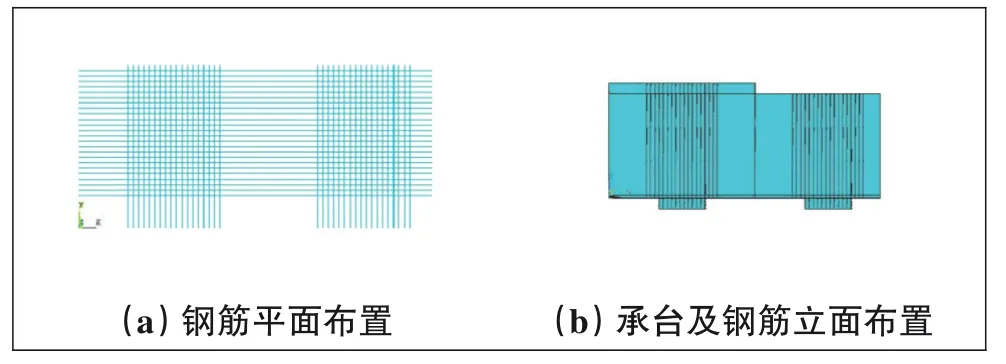
图9 8根1 m桩基承台实体配筋验算模型
通过对8个承台的三维实体计算发现,以拉压杆模型计算得到的钢筋数量完全符合承台受力要求,将钢筋直径变小进一步验算发现,利用该方法得到的钢筋还有一定富余量,各承台验算通过的钢筋数量与传统配筋方法的数量对比见表3。
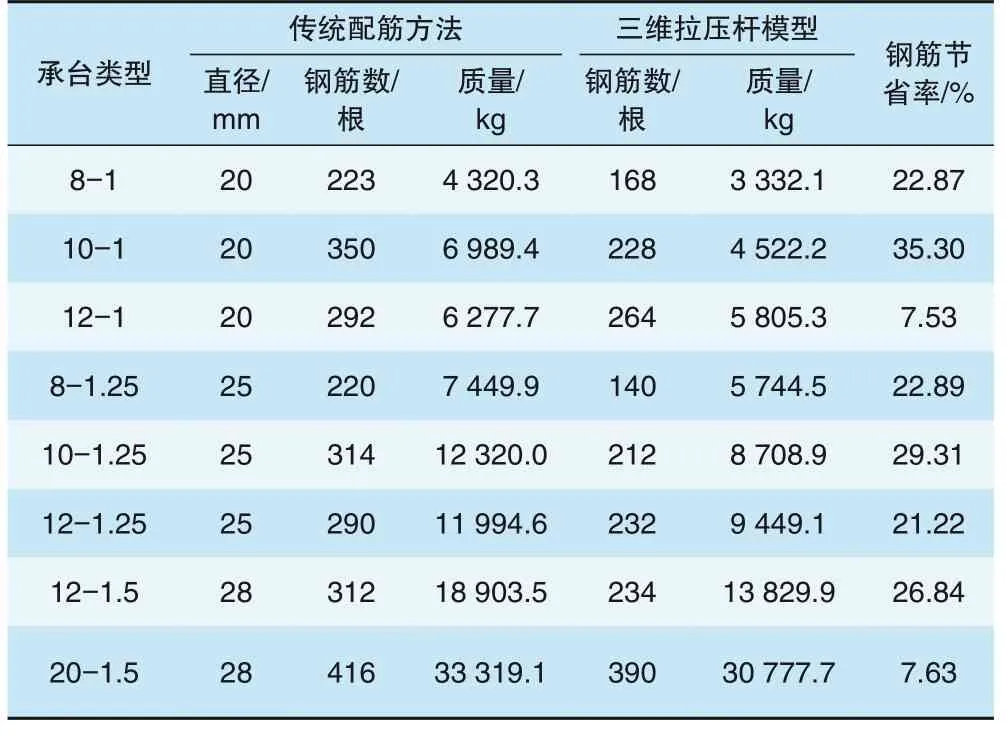
表3 各类型承台钢筋配筋计算比较
从表3可知,三维拉压杆模型计算得到的配筋数量比目前利用传统设计理论计算得到的钢筋能平均节省20%。原因其一为传统设计方法往往依据受弯模型,该模型并不能准确反映承台的受力特点;其二是传统配筋方法计算得到的钢筋均匀布置在承台底部,布置方式不合理,非拉杆位置的钢筋没有充分发挥作用。
因此,根据承台力流分析所建立的三维拉压杆模型,能够在设计中用于承台配筋计算,所得的配筋结果,受力合理又经济,可为未来铁路承台的设计乃至规范制定提供理论依据。
5 结束语
通过对铁路承台建立实体计算模型得到其力流规律,提炼出受力特点,建立三维拉压杆模型,并总结了拉压杆各节点的排布规律及尺寸取值。将三维拉压杆模型用于承台配筋计算,经验证是科学合理的,所得钢筋数量比传统配筋方法可节约20%。
三维拉压杆模型计算精度与实体模型相当,但可避免三维实体建模的复杂过程。在推广使用过程中,尚需注意承台的形状、桩基分布等特点是否与上述研究所列承台一致,如不一致,还需要增加承台的空间受力分析。但随着铁路承台设计工作的逐步推进,积累的承台模型逐步增多,三维实体模型的可适用范围也会慢慢增多。
