“24÷4”还是“8÷4”?
——低年级应用题教学问题的分析与启示
2021-12-18江苏省江阴市北大街小学
江苏省江阴市北大街小学 张 娜
【问题凝视】
二年级上册“除法”单元,练习中有这样一道应用题:

(1)把24本书平均分给3个小组,每个小组分得几本?
(2)你还能算出每人分得几本吗?
第一个问题几乎没有人错,24÷3=8(本),而第二个问题解答时,学生们的答案五花八门,主要有以下几种:①24÷4=6(本),②8+4=12(本),③4×2=8(本),④8÷4=2(本)。全班用第④种方法8÷4=2(本)的只有少数几人。通过对比交流,学生们一致否定了第二、第三种方法,而对于第一、第四种方法还是搞不清。很多学生认为第一问的得数是8本,第二问就应该用上第一问的得数来算。那么,到底是“24÷4”还是“8÷4”?
【成因透视】
这是一道图文结合、连续两问的应用题。因为第二问中没有告诉分本子的总数,学生就出现了思维障碍。那么,造成这种现象的原因是什么呢?
(一)学生没有养成良好的解题习惯
低年级学生在解题时往往急于求成,不读完题目就开始动笔,或者没有理解题意就急着解答,不知道怎样进行有条不紊的思考,这样就会导致很多不必要的错误发生。
(二)学生对于题意理解缺乏数量关系支撑
低年级学生抽象思维能力不够,不能灵活把握应用题的结构,不善于提炼数量关系。其实,这道题目除了可以根据“一共的本数÷分的人数=每人分得的本数”,还可以根据“每组本数÷每组人数=每人分得的本数”进行解答,而学生缺乏这方面的认知储备,也就无法与除法建立联系。
(三)学生对于计算方法缺乏理性思考
低年级的学生年龄小,不够理性,经常凭自己的感觉想加就加、想减就减,加法不对就用减法,减法不对就用加法。到二年级,学生学了乘法和除法之后,由于四种运算混在一起,学生更加区分不清楚了。如上述第二种答案和第三种答案就是属于这种情况。写第一种答案的学生,仅想着用本数去除以人数,却没有想清用哪个本数去除以人数才是正确的。
(四)学生对于解题结果缺乏对错评判
低年级学生思想简单,对得到的答案不去进行初步的评判。比如由第一问得到“每组8本”,再根据已知信息“每组有4人”,就可以判断第二问中算出每人6本、12本、8本都不可能,所以第一、二、三种答案都是错误的,继而重新选择正确的方法解答。
【出路审视】
应用题的教学贵在让学生站在理性的角度充分分析、理解题意,选择合适的方法,客观地解决问题。具体可以采取以下几个策略。
(一)把握“四清”原则,培养解题习惯
好的解题习惯是答对问题的重要保证。在平时的课堂教学中,要培养学生做到“四清”。即“读清”“想清”“写清”“查清”。
“读清”是做题过程中非常重要,而且能反映出学习能力的一个环节。读题一般先要“通读”,将所有的内容一字不漏地读一遍。二是“重点读”,就是结合题目圈出关键词和关键条件读。根据低年级学生注意力容易分散这一特点,教师可以要求学生手脑并用,用眼睛看,用手指读。
“想清”就是动笔前要想清每一句话的意思,特别是关键词要重点理解。可以想生活中的情况,也可以画线段图或简单实物图帮助理解,然后确定用什么方法计算。例如:求总数时,把两部分合起来用加法,求“几个几是多少”用乘法;已知总数,求其中一部分用减法,把总数平均分用除法。像这一题求每人分到几本,就是要把每组分到的本数平均分给4个人,所以应该用除法算。
“写清”就是在想清的基础上仔细列式计算,得到答案,要求数字抄对、计算正确。
“查清”包括在每题答完后要从答案的可能性上初步判断得数对错,也包括所有练习做完后需要重新读题理解题意,检查计算方法和答案的对错。
这四步的顺序不能颠倒。为了让他们牢牢地记住,养成“读清”“想清”的习惯,教师还可以用打比方的方法让他们记住“四清”原则。“读”“想”“写”“查”是四兄弟,“读”是大哥、“想”是二哥、“写”是三弟、“查”是四弟。他们按序排队,三弟不能插队到大哥或二哥的前面。当解答出现错误时,教师可以让学生分析一下自己在哪一步出了问题,是没“读清”还是没“想清”、是没“写清”还是没“查清”?长此以往,学生就能从无意识,到有意识,逐步养成良好的解题习惯。
(二)采用多元表征,增强题意理解
应用题的题意有多重表征方式,如利用现实情境中的实物、模型、图像或图画进行的形象表征,利用口语和书写符号进行的符号表征等,多元表征将帮助学生更好地理解题意。
例如:学生对于到底是“24÷4”还是“8÷4”存在疑虑的时候,教师可以创设分本子的情境。先把24本本子平均分成3份,放到每一组,每组几本?在学生明确做法后,教师追问:“要知道每人分到几本怎么办?”学生就会知道只要继续用每组的8本平均分成4份,得到每人2本。
结合分本子的过程,教师在黑板上逐步画出下图。这时,学生对24本本子两次平均分的过程就会理解得非常透彻。

所以,应用题课堂教学中,教师应带领学生通过多种形式理解题意,通过多元表征,让学生深深感受到解答应用题的过程中,一切应以题目本身的意思为准,而不能以个人的情感和意志为转移,逐渐养成良好的数学素养。
(三)提炼数量关系,建立方法联系
新课标明确指出,要从具体情境中抽象出数量关系,要从实际生活中给学生提供多种形式(如对话、文字、图表等)的条件和问题,培养学生逐步学会选择信息、重新组织信息、分析其中数量关系进而解决问题的能力。可见,数量关系的教学在应用题教学中占有重要的地位。
数量关系的提炼能帮助学生进行理性思维的培养,不能等到中高年级才开始,而是从低年级就要进行。但是低年级学生抽象思维能力弱,数量关系的提炼要在教师的辅助下进行,语言的表达要求不必太高,要适合低年级学生的理解能力和表达方式,可以比高年级具体形象一些。除了语言的表达,初学加减乘除应用题时,教师也可以根据题意结合符号的形式进行标注(如下图),目的是使学生理解清楚为什么用加、减、乘或除,使数量关系中的计算方法使用有根据,杜绝方法使用的随意性,促使学生根据数量间的关系建立理性思考。
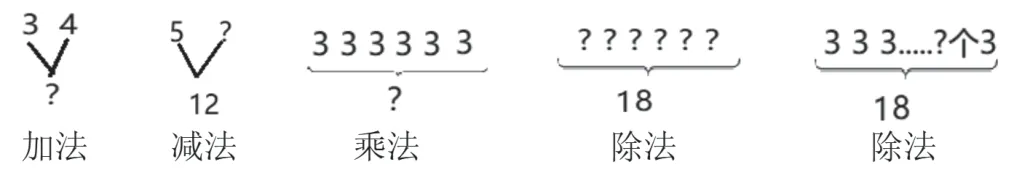
(四)适时提醒判断,强化检验意识
在日常教学中,教师要经常带领学生进行回顾和反思,针对实际情况进行检验。要把检验作为学生解答问题的必要步骤长期坚持,学生耳濡目染,就会逐步养成自觉检验的好习惯,变得更加严谨和细致。
例如本题中出现了四种不同答案:①24÷4=6(本),②8+4=12(本),③4×2=8(本),④8÷4=2(本)。教师就可以先问学生“这些答案中哪个肯定不对?”判断排除明显错误的答案,再进一步研究存在疑问的答案,这样既缩小了研究的范围,也强化了学生的检验意识,培养了学生思维的严谨性、批判性和深刻性。
【片段重构】
师:你还能算出每人分得几本吗?
生答,师在黑板上写出所有出现的答案:
①24÷4=6(本),②8+4=12(本),③4×2=8(本),④8÷4=2(本)。
师:这些答案中哪几个肯定不对?
生1:第2、3种。因为每人分几本,要把本子平均分,应该用除法计算。
生2:第2、3种。因为每组只有8本,每人的本数肯定不会比8本多,或者一样多。
师:那“每人分得几本?”到底是“24÷4”还是“8÷4”呢?
师:老师这儿有24本本子,我要把它们平均分给3个小组,谁会帮助老师分一分?
师:每组分到几本?
生:8本。
师:怎么列式?
生:24÷3=8。
师:为什么用除法算?24表示什么?3呢?8又表示什么?
师:我们用一共的本数÷组数=每组分到的本数。师:接下来我要知道每人分到几本怎么办?
生1:继续分。
生2:把本子平均分成4份。
师:那么,该用多少本平均分成4份呢?
学生都说8本。
师:8本?为什么不拿24本来分呢?(这是问题的关键,我得让学生仔细理解)
生1:24本本子是分给3个组的,不是分给一个组4个人的。
生2:因为24本本子已经平均分给3个组了,每个组分到8本,就要用每组8本平均分成4份。
师:所以,怎么计算每人分到多少本呢?
生:8÷4=2(本)。
师:这里的“8”表示什么?“4”呢?“2”又表示什么?
师:我们用一组的本数÷一组的人数=每人分到的本数。
接下来教师让学生回忆思考过程,并画图记录。
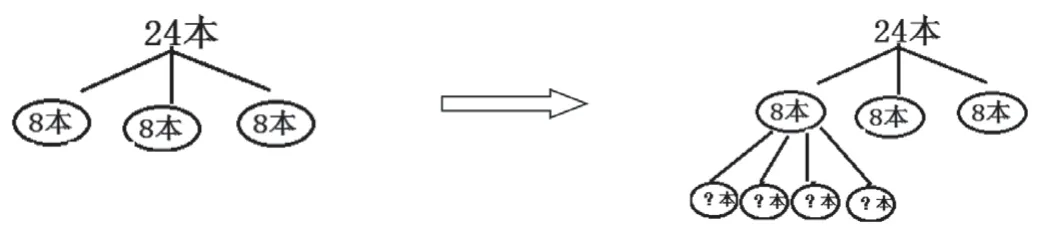
通过操作活动和画图,学生明确了“一共的本数÷组数=每组分到的本数”“一组的本数÷一组的人数=每人分到的本数”,已知份数要找对应的总数。
美国数学家哈尔莫斯说过,数学家X的一个漏失或一个误述,正好是数学家Y所需要用以发现真理的东西。学生(抑或教师)的一个差错,正好是教师所需要用以帮助学生发现真知的东西。所以,我们对待学生的差错,不能用“粗心”一词来打发。教师关于“错”之所以为“错”分析得越深,那么学生关于“对”之所以为“对”也就理解得越透。
