扩展的辅助函数法求一类非线性分数阶偏微分方程的精确解

张静

（南京财经大学 应用数学学院，江苏 南京 210023）

0 引言

非线性偏微分方程广泛应用于数学和物理学的各个分支，尤其是流体学、非线性光学.目前，已有很多方法用于获得非线性偏微分方程的精确解［1-11］.为找到一种求解方法简单直接，并能获得更丰富的精确解.杨健等［12］利用辅助函数法，借助数学软件Maple获得Benjamin-Bona-Mahonye（简称BBM）方程和Burgers方程的新精确解.此外，王书敏等人［13］利用修正的辅助函数法对非线性BBM方程进行求解，获得形式更为丰富的行波解.受此启发，考虑对辅助函数法进行推广，借助分数阶复变换和整合的分数阶导数的性质，研究时间分数阶modified Benjamin-Bona-Mahony（简称mBBM）方程和（3+1）维非线性分数阶Jimbo-Miwa方程的精确行波解.

1 预备知识

首先给出几个概念，为后续研究做准备.整合的分数阶导数定义及基本性质如下.

设f:(0,∞)→R，f的α阶导数定义为：，t＞0，0＜α≤1.

基本性质［14］设α∈(0,1]，f=f(t)，g=g(t)，在t＞0时可微并有

性质1，a,b∈R,

性质2，μ∈R,

性质3,

性质4.

2 扩展的辅助函数法

对于分数阶非线性偏微分方程

其中u=u(x,t)，是u关于x和t的整合分数阶导数，P是u和u的关于x和t的各阶偏导数的多项式.

扩展的辅助函数法分为3步.

步骤1对方程（1）作分数阶复变换，

其中k、l是任意非零常数.将方程（1）转化为常微分方程，

步骤2假设方程（3）的精确解具有如下形式，

其中ai为待定系数，而幂级数的最高次幂n通过平衡常微分方程的非线性项和最高阶导数项来确定.

F(ξ)满足一般的Riccati方程

对应的辅助方程的解有，

①当A=B=0时，

②当A=0,B≠0时，

③当C≠0，Δ=B2-4AC＞0时，

④当C≠0，Δ=B2-4AC＜0时，

⑤当C≠0，Δ=B2-4AC=0时，

其中C1，C2为积分常数.

步骤3通过常微分方程获得非线性代数方程组.把假设的具有式（4）形式的解和一般Riccati方程（5）代入方程（3）中，合并F(ξ)的同次幂项，并令其各项系数和为零，由此得到形式解（4）中各项的含系数ai，c，l的非线性代数方程组，利用吴消元法求解这组代数方程组，并将ai代入解（4），c，l代入式（6）～（12）中，结合式（2），即得分数阶偏微分方程的精确行波解.

3 方法应用

3.1 时空分数阶mBBM方程

考虑如下时空分数阶mBBM方程

对方程（13）做分数阶复变换，

其中k、l是任意非零常数.将式（14）代入式（13）并化简可得，

由式（15）中的φ2φ'(ξ)和φ‴(ξ)，得到n=1.可设方程解的形式如下，

将式（16）和方程（5）代入式（15），然后合并F(ξ)的同次幂项系数，得到非线性代数方程组并求解得，

其中k为任意常数.将所求得的式（17）代入式（16）得到时空分数阶mBBM方程的形式解为，

再将式（6）～（12）的结果分别代入式（18）可获得如下5组解：

①当A=B=0时，

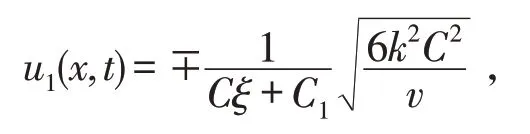
②当A=0,B≠0时，

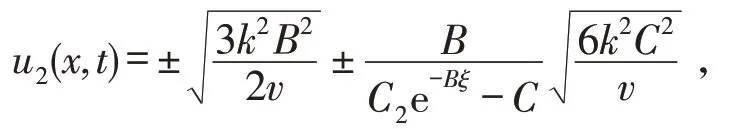
③当C≠0，Δ=B2-4AC＞0时，

④当C≠0，Δ=B2-4AC＜0时，

⑤当C≠0，B2-4AC=0时，

图1 取正向u7(x,t)的三维图

图2 取负向u7(x,t)的三维图

3.2 （3+1）维非线性分数阶Jimbo-Miwa方程

考虑如下分数阶Jimbo-Miwa方程

对方程（19）做分数阶复变换，

其中ω是任意非零常数.将式（20）代入式（19），令φ'=v并化简可得，

由式（21）中的vv'(ξ)和v‴(ξ)，得到n=2.可设方程解的形式如下，

将式（22）和方程（5）代入式（21），然后合并F(ξ)的同次幂项系数，得到非线性代数方程组并求解得，

情形1

将所求得的式（23）代入式（22）得到分数阶Jimbo-Miwa方程的形式解为，

再将式（6）～（12）的结果分别代入式（24）可获得5组解：

①当A=B=0时，

②当A=0,B≠0时，

③当C≠0，Δ=B2-4AC＞0时，

④当C≠0，Δ=B2-4AC＜0时，

⑤当C≠0，B2-4AC=0时，

情形2

将所求得的式（25）代入式（22）得到分数阶Jimbo-Miwa方程的形式解为

再将式（6）～（12）的结果分别代入式（26）同样可获得如下5组解：

①当A=B=0时，

②当A=0,B≠0时，

③当C≠0，Δ=B2-4AC＞0时，

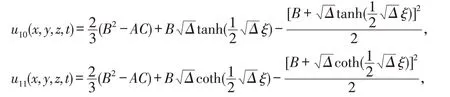
④当C≠0，Δ=B2-4AC＜0时，

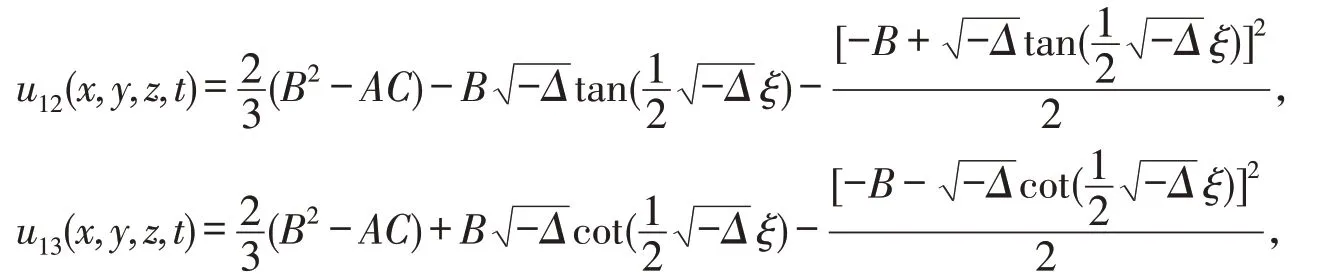
取A=B=C=2,η=β=γ=1,y=0,z=2,的图像如图3、图4所示.

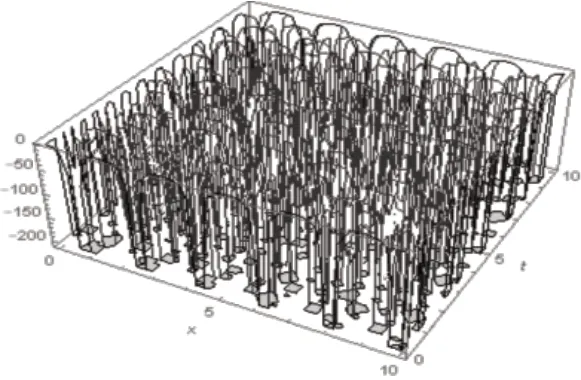
图3 u12(x,y,z,t)的三维图

图4 u13(x,y,z,t)的三维图

⑤当C≠0，B2-4AC=0时，

4 结语

综上，本文推广辅助函数法，将F(ξ)满足的方程F'(ξ)=F(ξ)2+λF(ξ)+μ推广到满足一般的Riccati方程F(ξ)'=A+BF(ξ)+CF(ξ)2上，利用该方法得到时间分数阶mBBM方程以及（3+1）维非线性分数阶Jimbo-Miwa方程的新精确解.并运用mathematica绘出部分精确解取不同值的三维波形图.同样的该方法也可以运用到求其他时间分数阶、空间分数阶微分方程（组）的精确行波解中.