奥氏体不锈钢上缺陷涡流探头POD新模型

王静,凌元锦

(青岛科技大学环境与安全工程学院,山东青岛266042)

压力容器是现代工业生产中的重要组成部分之一。为了保障设备在运行过程中能够稳定运行,需要对压力容器进行定期的检查[1-2]。压力容器内部通常会覆盖奥氏体不锈钢层,来增加压力容器的耐腐蚀性,但是当含氯离子的流体流入压力容器时,压力容器内部也会很容易产生点蚀[3-4]。因此,无损检测对于检查压力容器内表面的完整性和设备的安全运行来说就显得尤为重要。无损检测是在不损害或不影响被检测对象使用性能的前提下,采用涡流、超声等检测技术来判断被检对象内部结构、状态与性质的检测技术的总称[5]。

涡流检测是检测此类缺陷的一种潜在方法。涡流检测对工件表面上或附近的缺陷具有很高的检测灵敏度,并且在一定范围内具有良好的线性指示[6]。但是,由于奥氏体不锈钢焊缝的表面比较粗糙,在进行涡流检测时会产生高水平的噪音。当缺陷的尺寸较小时,噪声信号将会覆盖涡流缺陷信号,从而导致测试结果出错。为了更加准确地评估缺陷的检出概率,有必要更概率地量化涡流探头的检测能力,以便进行后续分析。

为了解决这一问题,缺陷检出概率(POD)被使用来量化涡流探头的检测结果。POD的主要概念是在给定的检测条件和工艺下,能够检测出某一缺陷尺寸范围的可能性,它代表了无损检测方法缺陷检测的能力[7-9]。POD 不仅有助于量化非破坏性测试方法,而且有助于基于风险的维护[10-11]。传统的POD 模型是定义缺陷检测信号大于预定义决策阈值,则说明该缺陷可以被检测出。但是,POD 曲线会随决策阈值的变化而发生改变,没有明确的理由说明哪一个决策阈值是合理的。

在此背景下,本工作中提出了一种新的POD模型,该模型对传统的POD 模型进行改进,不是定义固定的决策阈值去评估缺陷的检出能力,而是采用随机选取决策阈值的方法。所提出的方法可以使缺陷检测能力不受主观因素影响而呈现出POD 曲线的唯一性。在本研究中,制备了6块覆盖奥氏体不锈钢包层的焊接板样品,板上被钻有43个不同尺寸的人工钻孔,来模拟大型压力容器内表面上的腐蚀点。实验结果表明,本工作提出的新的POD 模型对于评估涡流探头在奥氏体不锈钢中缺陷的检测能力更为合理。

1 样品制备和涡流检测

1.1 板样品的制作

这项研究制备了9块板状样品,板表面覆盖了奥氏体不锈钢层,以模拟大型压力容器的内壁。由于奥氏体不锈钢材料价格较高,而且制造的过程中有许多不同于低合金钢和碳素钢的特殊要求,综合各种条件考虑,所以本工作中板样品采用了复层为奥氏体不锈钢的钢板作为样品。图1说明了板样品的具体细节。样品的基层金属是钢板(SM490 或ASTM A387 Gr22),其长度为251～401 mm,宽度为112～175 mm。覆盖层材料为US-B309L,厚度约5 mm。焊缝的宽度为50～70 mm。6个板样品上被钻有不同直径和深度的人工钻孔(如图1 所示),以模拟压力容器内部的点蚀。样品包含的钻孔的数量取决于焊接板样品的尺寸。表1列出了与每对直径和深度相对应的钻孔数量,总共制备了85个钻孔。钻孔之间的间距为30 mm(如图1 所示)。在本实验中,还准备了3块无缺陷的板样品作为对照组,以获取噪声数据。

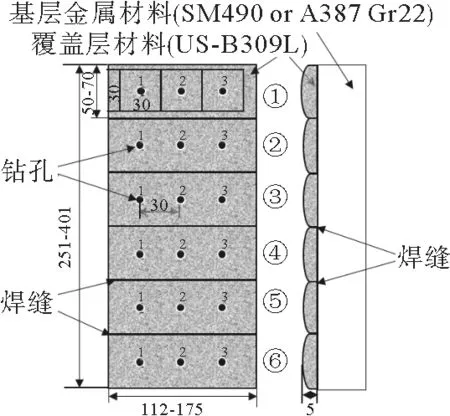
图1 奥氏体不锈钢样品Fig.1 Sample of Austenitic stainless steel

表1 钻孔的数量Table 1 Number of drilled holes /mm

1.2 涡流检测

涡流检测实验中使用了均匀涡流探头和商用涡流测试仪(aect-2000N,日本大阪)来采集数据。探头的尺寸如图2所示。检测过程中采用的激励频率为100 k Hz。在检测过程中涡流检测探头被固定在XYZ平台上,探头距板平面的垂直高度为1 mm,由电脑控制平台来回移动探头扫描检测区域,通过探头扫过扫描区域而获取缺陷信号,然后由AD 转换器将采集的信号以数据的形式呈现在电脑上。探头的扫描区域是一个以钻孔为中心的30 mm×30 mm 正方形区域(如图1所示)。扫描的间距在样品的横向和纵向分别为500和100μm。

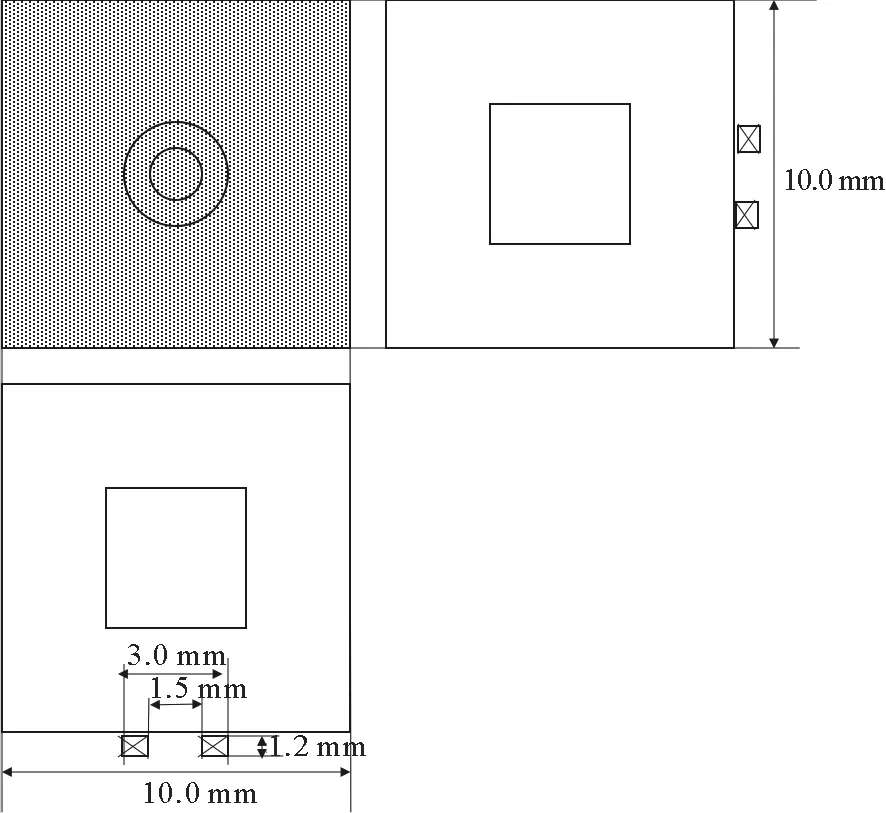
图2 探头的尺寸示意图Fig.2 Schematic of probe size

在实验之前,需要对仪器进行校准,以使涡流检测探头在标准材料板(耐腐蚀合金Inconel600)上分别由长度、深度和宽度分别为20、5、0.5～0.6 mm的人造焊缝引起的最大信号变为1.0 V 和0°。校准使得在人工缝隙处的最大振幅控制在10 mm×10 mm的正方形区域中。因此,由于缺陷引起的信号包含在围绕钻孔的10 mm×10 mm 正方形区域中。然后,以相同的方式提取噪声。

2 POD 分析

这项研究采用了两种POD 模型:传统POD 模型和新提出的POD 模型。

传统POD模型采用的是vsa方法,这种方法适用于数量较少的样本。此方法假定裂纹尺寸(a)和信号幅度)之间呈线性关系。然后,为了获得合适的表达式来表达它们之间的相关性,通常采用对数变换来满足它们之间的线性关系。关系可以写成

其中ε是噪声项,均值为零且标准偏差为σ的正态分布。β0,β1,σ是通过简单的回归分析获得。vsa方法是当缺陷信号幅值超过给定的决策阈值时,则说明缺陷可以被检测出,即P(a)＝P(≥)。该方法具体的过程和详细信息可以在USDOD 和ASM 手册中找到[8-9]。

这项研究中,提出的新POD 模型使用随机决策阈值,而不在使用固定决策阈值()来评估检测信号超过噪声信号的概率。该模型第一步需要分别评估缺陷信号和噪声信号的分布。第二步假定裂纹尺寸(a)和信号幅度(^a)之间呈线性关系。然后,选择合适的表达方式来表达它们之间的相关性,本工作中所有数据均采用了对数变换。第三步是在一个缺陷参数下随机和独立的分别从缺陷函数的分布和噪声的分布中抽取一个样本数据。比较两个数据的大小以确定缺陷是否可以被检测出来。如果缺陷信号大于噪声信号,则将其记录为“命中”,否则将其记录为“未命中”。最后,在一个缺陷参数下,随机抽取n次并比较n次抽取数据的大小以评估“命中”的概率。在本工作中,随机抽样和独立比较一百万个样本,最终值趋于稳定。则该比率即为某一缺陷参数下的POD 值。

3 结果与讨论

图3～4总结了传统POD 分析的结果。在本研究中,所有缺陷参数和信号幅值均被做了对数变换,评估缺陷参数和信号幅值之间的线性关系,如图3(a)和图4(a)所示。这里值得注意的是图3～4中在计算传统POD 曲线时均选取的是95%的噪声作为决策阈值。图3(b)揭示了信号幅值与参数深度之间的关系,从中可以观察到深度作为缺陷参数是不可靠的,因为它存在较大的置信区间。相反,图4(b)显示的缺陷直径作为参时,直径和信号幅值的置信区间要窄得多。因此,这就暗示直径作为参数更合理。为了进一步确认使用单个直径作为参数是否合理,所以进行了进一步的评估,评估了参数对信号幅度的影响程度。表2总结了当直径作为参数时,检出概率的数值。从表2中可以发现,当直径作为参数时,直径大于3 mm 时,无论深度如何变化,缺陷引起的信号总是大于噪声的最大幅值,说明缺陷可以被检测出来。实验结果表明直径作为参数是合理的,并且深度对检出概率影响可以忽略。

图3 缺陷深度与信号幅值之间的关系变化Fig.3 Results of regression and POD analysis when the depth was used as a parameter

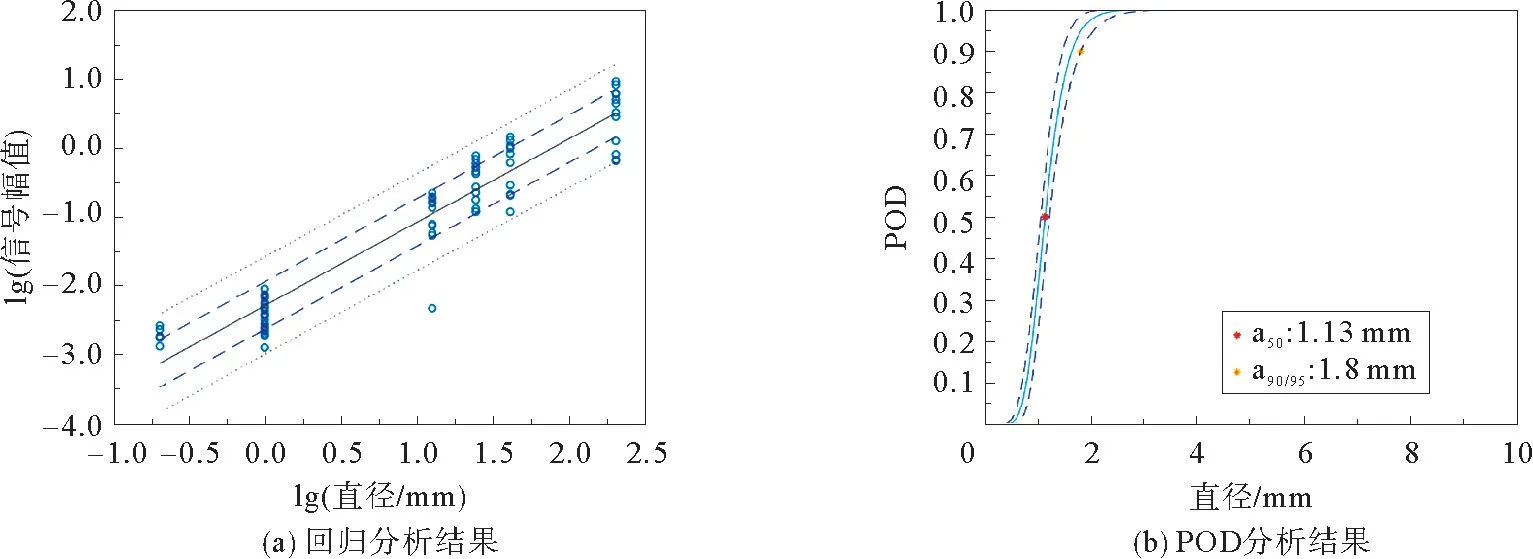
图4 缺陷直径与信号幅值之间的变化关系Fig.4 Uniform probe results of regression and POD analysis when the diameter was used as a parameter

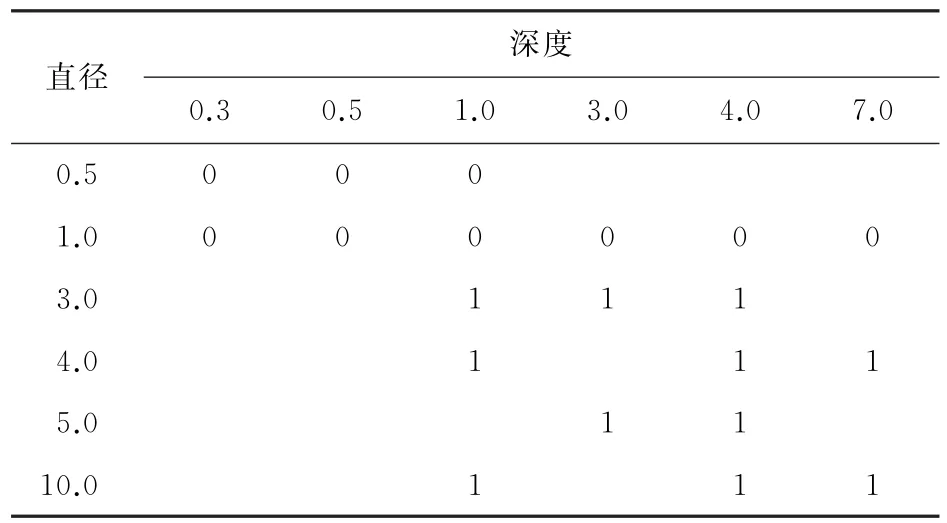
表2 缺陷的检出比例Table 2 Ratio of detected drill holes /mm

图5是选取的是不同决策阈值下传统POD 曲线的变化,从图5中可以发现,随着决策阈值的变化POD 曲线也发生了明显的改变。图6是使用新模型计算获得的POD 曲线。图4和图6结果表明本工作提出的新的POD 模型评估涡流探头对奥氏体不锈钢中缺陷的检测效果更好。

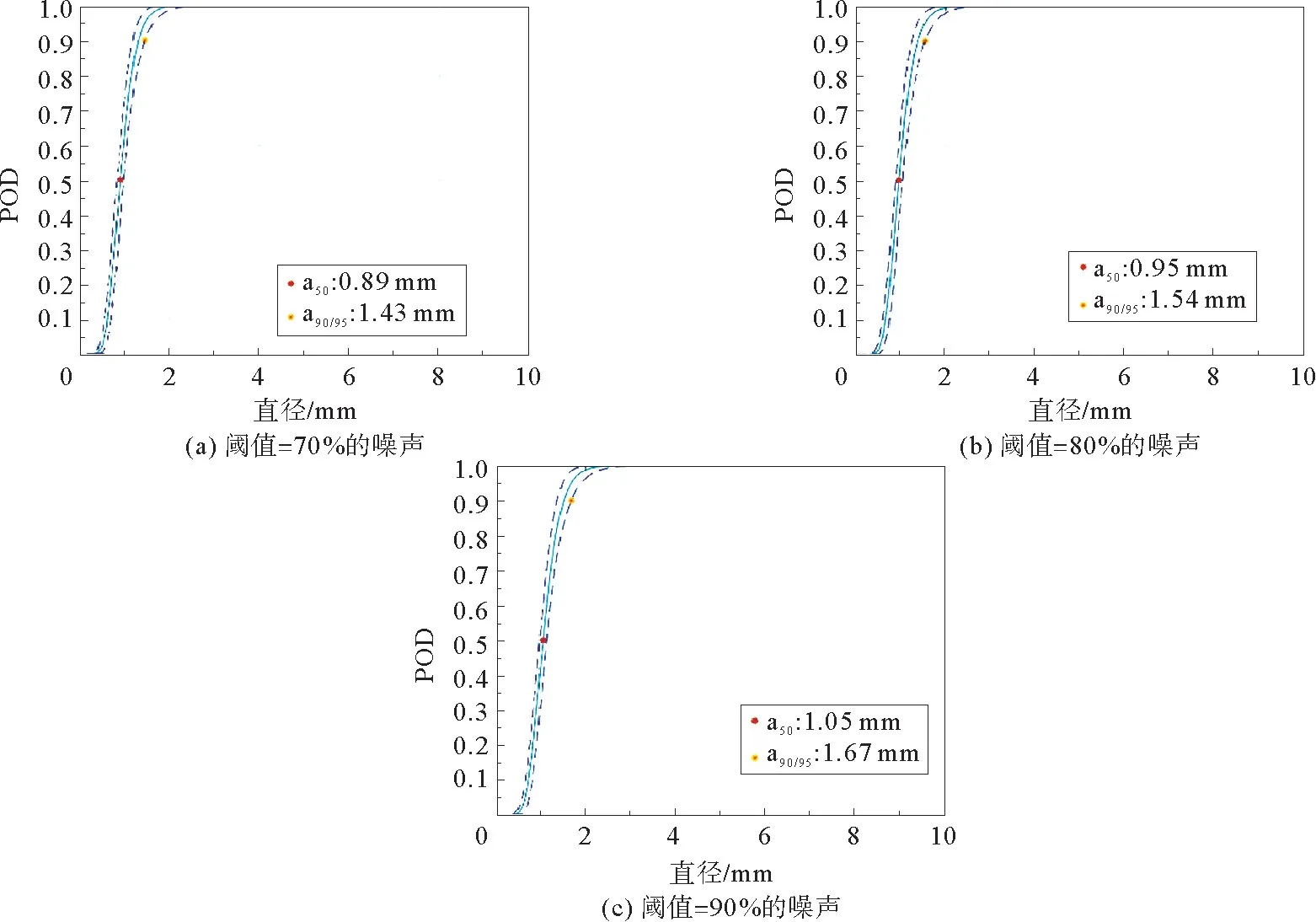
图5 不同决策阈值下的传统POD曲线Fig.5 Traditional POD curve under different decision thresholds

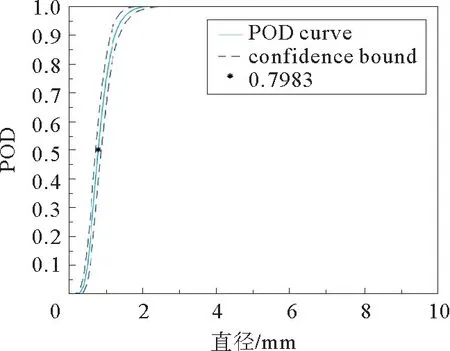
图6 新提出的POD曲线Fig.6 Novel proposed POD curve

4 结语

提出了一种基于随机决策阈值的新的POD 模型,用于评估涡流探头在奥氏体不锈钢中缺陷的检测能力。提出的新模型是对传统的POD 模型的改进,采用随机选取决策阈值的方法,不受主观因素的影响,检测结果呈现出一条独立的POD 曲线。实验结果表明,该模型评估涡流探头在奥氏体不锈钢中缺陷的检测能力更为合理,优于传统POD 模型。