蜂窝密封泄漏特性与动力特性影响因素分析

2021-12-17肖忠会孟继纲

风机技术 2021年5期

周敏孙丹肖忠会孟继纲姚洁

（1.沈阳航空航天大学航空发动机学院辽宁省航空推进系统先进测试技术重点实验室；2.沈阳鼓风机集团股份有限公司辽宁重大装备制造协同创新中心）

0 引言

密封作为透平机械的重要部件，起着减少工作介质泄漏的作用[1-2]。蜂窝密封由于具有良好的封严性能和动力学特性被广泛应用[3-4]。随着工作介质不断向高参数方向发展，蜂窝密封在工作过程中会产生较大的气流激振力，造成转子失稳[5]。研究表明，蜂窝密封的结构参数与预旋是影响转子失稳的重要因素。

Kaneko[6]通过实验数据对比得出，倾角型蜂窝密封具有更大的直接阻尼系数与较小的交叉刚度系数。Kleynhans[7]采用双控体方法分析了孔深对蜂窝密封动力特性的影响规律，结果表明，孔深不会改变蜂窝密封的穿越频率。孙丹[8]等数值分析了蜂窝密封泄漏量的影响因素，构造了考虑结构参数及工况参数的蜂窝密封泄漏量计算公式。Childs[9-11]实验研究了多种结构蜂窝密封的动力特性。研究发现，芯格尺寸对密封动力特性系数影响很大。Anthony[12]通过数值与实验得出，发散间隙蜂窝密封具有较大的直接阻尼系数，其转子稳定性最好。Dawson[13]采用多频方法计算了在涡动频率对蜂窝密封的动力特性系数的影响规律，发现有效阻尼系数随着频率的增大先增大后减小。Giuseppe[14]计算了不同进口预旋下蜂窝密封的有效刚度系数和有效阻尼系数，结果表明，随着预旋的增大，蜂窝密封稳定性下降。晏鑫数值研究了预旋、对边距与孔深对蜂窝密封泄漏流动的影响。Tony[15]实验研究发现进口预旋对蜂窝阻尼密封有效刚度系数的影响较小，主要用过影响交叉刚度系数来较低其有效阻尼系数。Kraemer[16]等研究了密封结构引起的转子失稳原因及工况对密封交叉刚度的作用规律，并对消除失稳故障提出了一系列措施，如采用增加阻尼、缩短密封长度和反旋流等。现有文献中对影响蜂窝密封动力特性的因素考虑较为单一，当多种因素相互耦合时，蜂窝密封动力特性系数的变化规律仍需进一步探索。

针对于蜂窝密封动力特性考虑单一的问题，本文研究了孔深、对边距、轴向长度对蜂窝密封性能的影响规律。分析了结构参数和进口预旋对蜂窝密封静力与动力特性的影响，并揭示了预旋影响密封稳定性的机理。

1 密封动力特性理论分析

1.1 密封气流激振力线性化模型

转子在密封中椭圆涡动轨迹示意图如图1所示，

由小位移理论可知，转子受到的气流激振力Fx，Fy与扰动位移、扰动速度的关系可线性化表示为：

式中，x，y为转子涡动位移；x'，y'为转子涡动速度。

1.2 转子多频椭圆涡动模型

转子的涡动方程可由复数方程表示为：

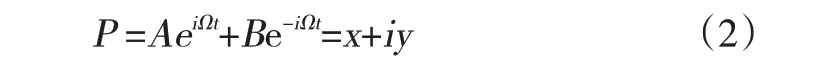
其中的A，B都是常值函数，设A=a1+ia2，B=b1+ib2。由欧拉方程eiθ=cosθ+isinθ，将A，B的值带入到上式得

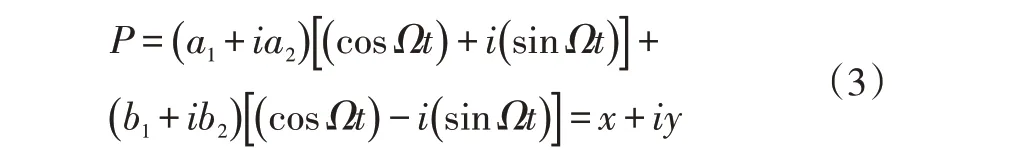
根据对应项系数相同可得：

若取a1+b1=0，b2-a2=b，a2+b2=a，a1-b1=0 或a1+b1=a，b2-a2=0，a2+b2=0，a1-b1=b。

假设转子涡动包含N种频率，各个涡动频率下的转子涡动振幅相等，则转子多频涡动的方程为：

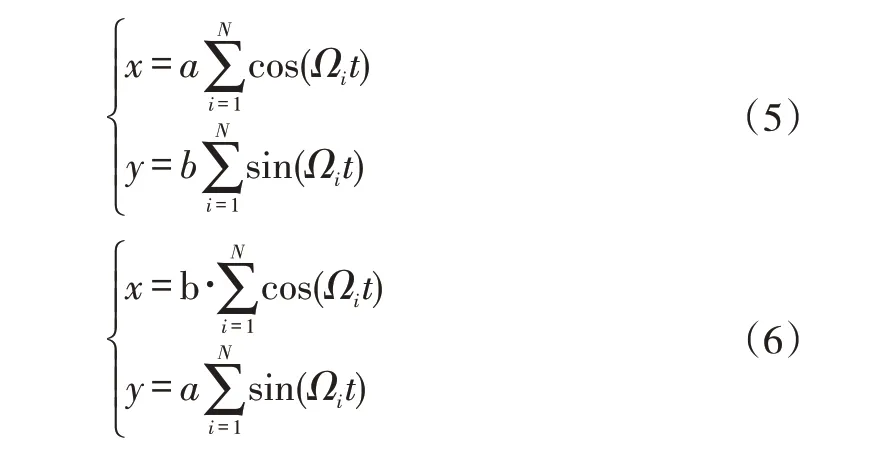
将式（1）进行快速傅里叶变换（FFT），可得到：

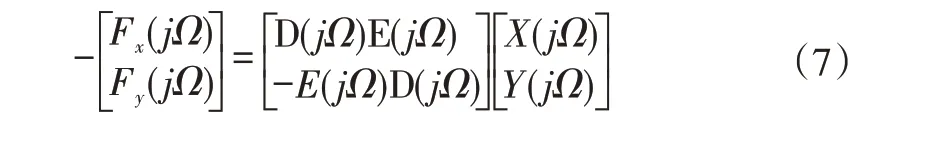
E(jΩ)=k(Ω)+jΩ·c(Ω)为阻抗函数。通过求解式（7）可得：

最终可得频率解为：

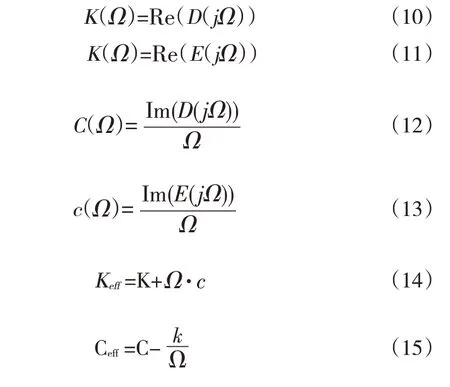
有效刚度Keff和有效阻尼Ceff越大，越有利于转子的稳定[19]。

2 蜂窝密封实验研究

设计搭建了蜂窝密封泄漏量测试实验台，如图2所示。密封实验系统包括两大部分：试验主体部分和测试系统部分。试验主体部分又分为：转子-轴承-密封系统、气流力放大系统、不平衡调节系统、传动及控制系统、润滑系统、供气系统。进气压力可调，并能在一定的时间内保证持续稳定供气，进气方式设计成部分进气和全周进气可调。为了使高压气流对转子的气动冲击力互相抵消，采用中间进气的方法，通过密封齿与转子轴套之间的间隙，从两端排出。轴两端支撑采用圆瓦滑动轴承。气缸结构设计成上下两半，通过螺栓上下扣紧联接，方便更换不同的密封型式。气缸内壁沿周向设有燕尾槽，试验密封安装于槽内。从中部往两端对称布置试验密封。对应密封件中间设置多个测量孔，可以加装涡流传感器和压力传感器。

图3 为蜂窝密封试验件。将蜂窝密封实验件安装在气缸上，再将装有密封件的气缸安装在密封实验台上并固定，对气缸进行密封，调节实验气缸和转子的同心，将气路安装在气缸上并检查其密封性能。本实验中同一工况下的蜂窝密封经过三次测量取其泄漏量平均值。

3 蜂窝密封数值研究

图2 密封泄漏量测试实验台Fig.2 Seal leakage test bench

图3 蜂窝密封试验件Fig.3 Test sample of honeycomb seal

3.1 求解模型

本文计算的蜂窝阻尼密封结构图如图4所示，蜂窝阻尼密封主要由密封套，密封体与蜂窝带组成，具体结构参数如表1所示。

3.2 网格划分

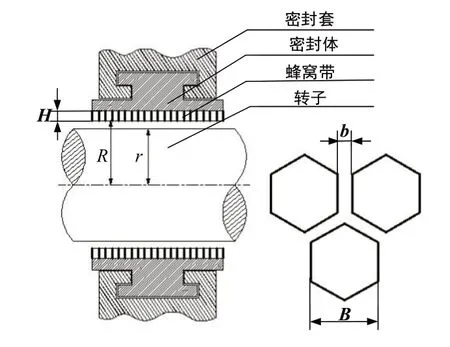
图4 蜂窝阻尼密封结构图Fig.4 Structure diagram of honeycomb seal

表1 蜂窝阻尼密封结构参数Tab.1 Structural parameters of honeycomb damping seal

本文采用周期性建模，以一个整排和两个半排作为最小的周期循环单元。密封间隙采用线网格，其余部分采用面网格。其网格划分如图5 所示。具体数值如表2所示。

3.3 边界条件

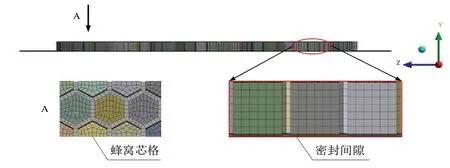
图5 网格划分Fig.5 Grid of the honeycomb seals

表2 网格划分属性Tab.2 Grid meshing

表3 给出了蜂窝密封泄漏量与动力特性系数求解模型的边界条件。将周期性模型旋转成整周模型，设定进口面为总压、总温，进气沿着轴向方向。

3.4 数值模型准确性验证

为验证本文蜂窝密封求解模型的准确性，本文给出了结构参数为B3H3L96的蜂窝密封泄漏量数值与实验对比结果如图6 所示，从图中可以看出，随着进出口压比的增大，蜂窝密封的泄漏量呈线性增加。当进出口压比为5时，蜂窝密封数值计算与实验测量的泄漏量最大，其相对误差为11.9%。由于实验台装配时存在一定配合间隙，在转子转动过程中存在涡动，转静子之间的密封间隙发生轻微变化。同时，蜂窝密封数值仿真是理想化模型，计算模型进气为轴向进气，实验气缸为径向进气，轴向出气，模型存在简化，造成实验与数值结果存在偏差。两种方法所得到的蜂窝密封泄漏量基本吻合，从而验证了本文求解模型的准确性。

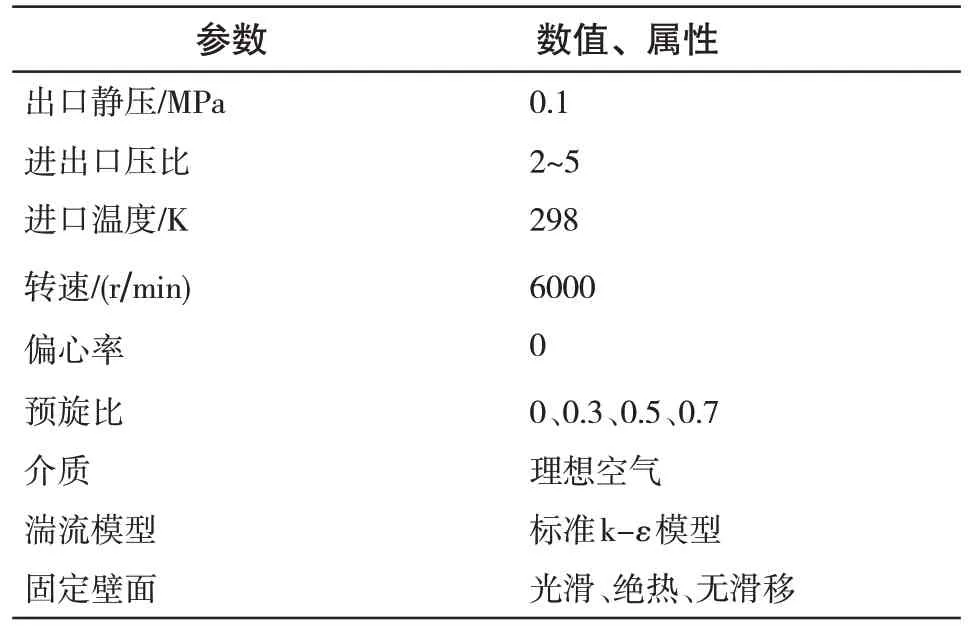
表3 边界条件Tab.3 Boundary conditions of solution model

4 数值计算结果分析

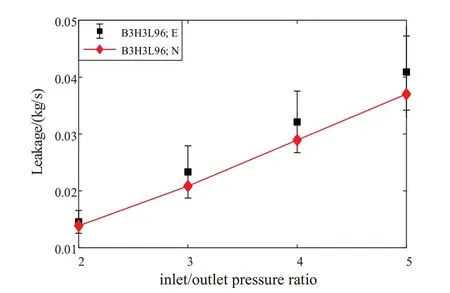
图6 泄漏量数值与实验对比结果Fig.6 Comparison of seal leakages between numerical simulation and experimental test

4.1 芯格尺寸对蜂窝密封性能的影响

由图7 中可以看出，随着蜂窝密封孔深的增加，密封泄漏量先增加后减小，主要是芯格孔内旋涡状态影响密封的封严性。随着对边距的增加，密封泄漏量增大，主要是当轴向长度相等时，增加对边距会减少密封轴向上芯格的数量，减弱了密封内部整体的耗散能力。

图7 芯格尺寸对蜂窝密封泄漏量的影响Fig.7 Effects of cell size on leakage of honeycomb seal

从图8(a)～(d)中可以看出，随着涡动频率的增加，Kxx和Cxy均增加，而Kxy和Cxx减少。从图8(e)～(f)中可以看出，有效刚度系数随着涡动频率的增加而增大。当涡动频率小于80Hz 时，有效阻尼系数随着涡动频率的增大而增大，反之则减小。当有效刚度系数均为正时，有效阻尼系数越大，密封稳定性越好。

4.2 轴向长度对蜂窝密封性能的影响

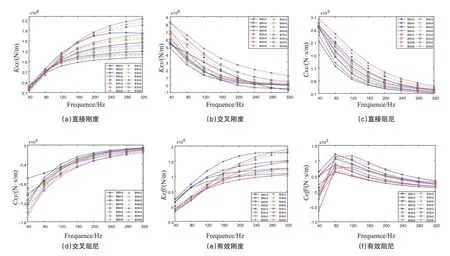
图8 芯格尺寸对蜂窝密封动力特性的影响Fig.8 Effects of cell size on dynamic characteristics of honeycomb seal

由图9可以看出，蜂窝密封泄漏量随着轴向长度的增加而减小。这是由于相同蜂窝密封芯格尺寸，增大轴向长度会增加总体旋流数量，加强了密封内部整体的耗散能力，从而密封泄漏量减少。同时也可以看出，蜂窝密封泄漏量随着压比的增大均呈增长趋势，这是由于压比越大，气体流速增加，透气效应大于湍流的耗散作用，故泄漏量开始增大。

从图10中可以看出，随着压比的增大，蜂窝密封的Kxx，Kxy与Cxx均增大，而Cxy呈减少趋势。同时也可以看出，在同一压比下，随着轴向长度的增加，蜂窝密封Kxx，Kxy与Cxx增大，而Cxy减少。由有效刚度阻尼图形可知，当结构参数相同时，蜂窝密封的有效刚度和有效阻尼系数随着轴向长度的增加而增大。

4.3 预旋对蜂窝密封性能的影响

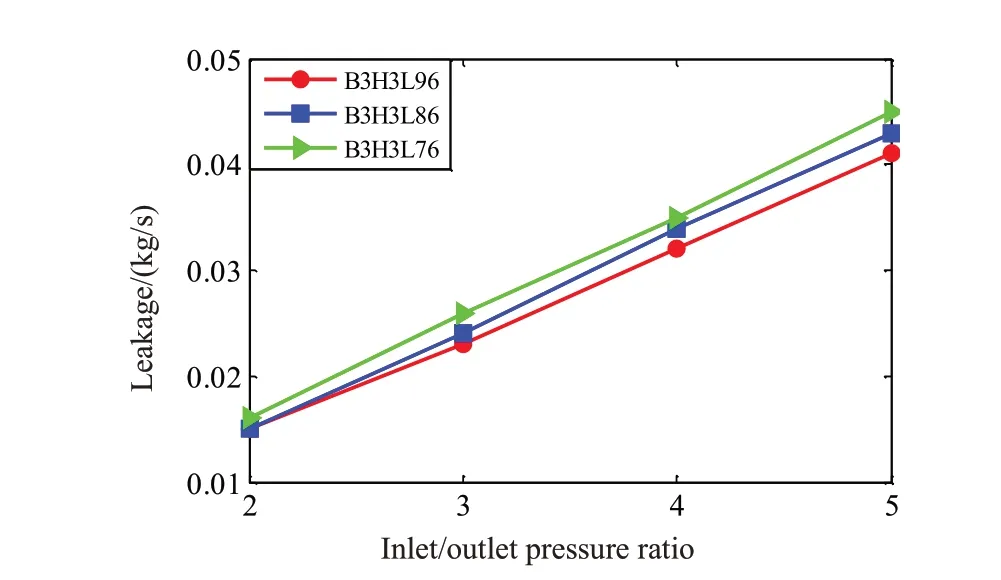
图9 轴向长度对蜂窝密封泄漏量的影响Fig.9 Effects of axial length on leakage of honeycomb seal

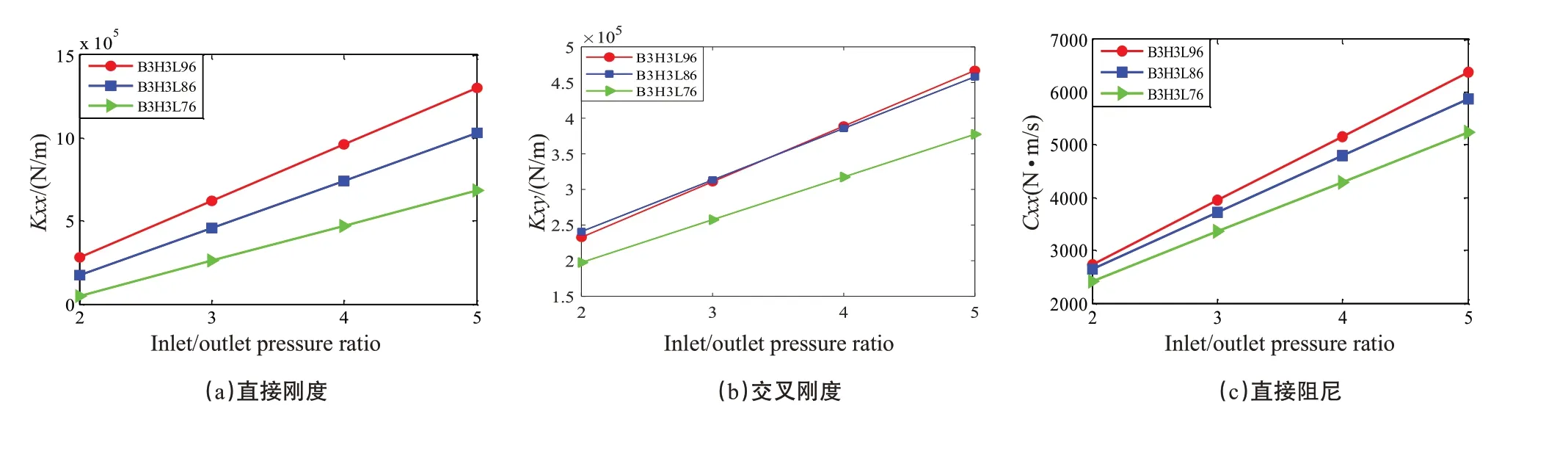
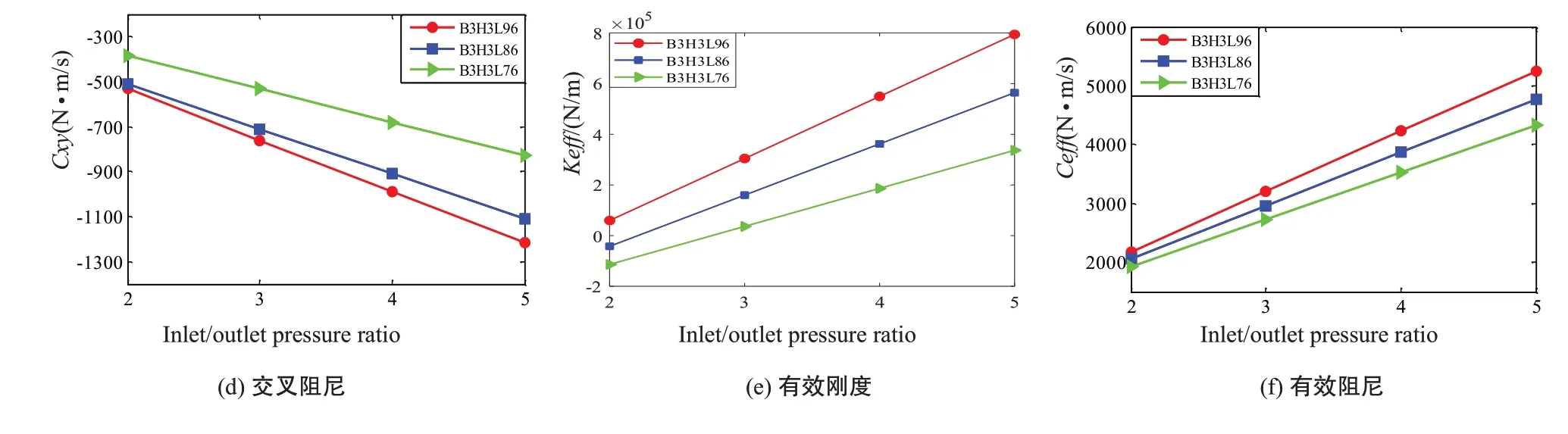
图10 轴向长度对蜂窝密封动力特性的影响Fig.10 Effects of axial length on dynamic characteristics of honeycomb seal

从图11 可以看出随着进出口压比的增大，蜂窝密封泄漏量增加。在相同压比下，随着预旋比的增大，蜂窝密封泄漏量减少。泄漏量减少主要是由于随着预旋比的增大，气流周向分量增大，轴向分量减小。当压比为2，预旋比为0 时，泄漏量为0.014547kg/s，预旋比为0.7 时，泄漏量为0.014297kg/s，泄漏量降低了1.71%，预旋对蜂窝密封泄漏量影响较小。

图11 预旋比对蜂窝密封泄漏量的影响Fig.11 Leakage of honeycomb seal under different inlet preswirl ratios

图12为x激励下，非定常计算t=0.5s时刻，4种进口预旋比下(λ=0，0.3，0.5，0.7)，蜂窝密封腔室内的压力分布和转子表面流体激振力矢量图。在此时刻，转子运动到x轴上的A点，其涡动速度沿转子与椭圆轨道的切线方向。从图中可以看出，随着预旋比的变化，密封腔室内相对高压位置不断改变，从而导致密封气流激振力大小和相位角的改变。密封径向气流力方向与转子偏心方向相反，可促使转子向轴心方向移动，有利于转子系统的稳定。密封切向气流力为负值与转子涡动方向相反，可抑制转子涡动，提高稳定性，当预旋比从0增加到0.7时，密封切向气流力的绝对值不断减小，对转子涡动的抑制作用减弱，从而使得转子不稳定性显著提高。

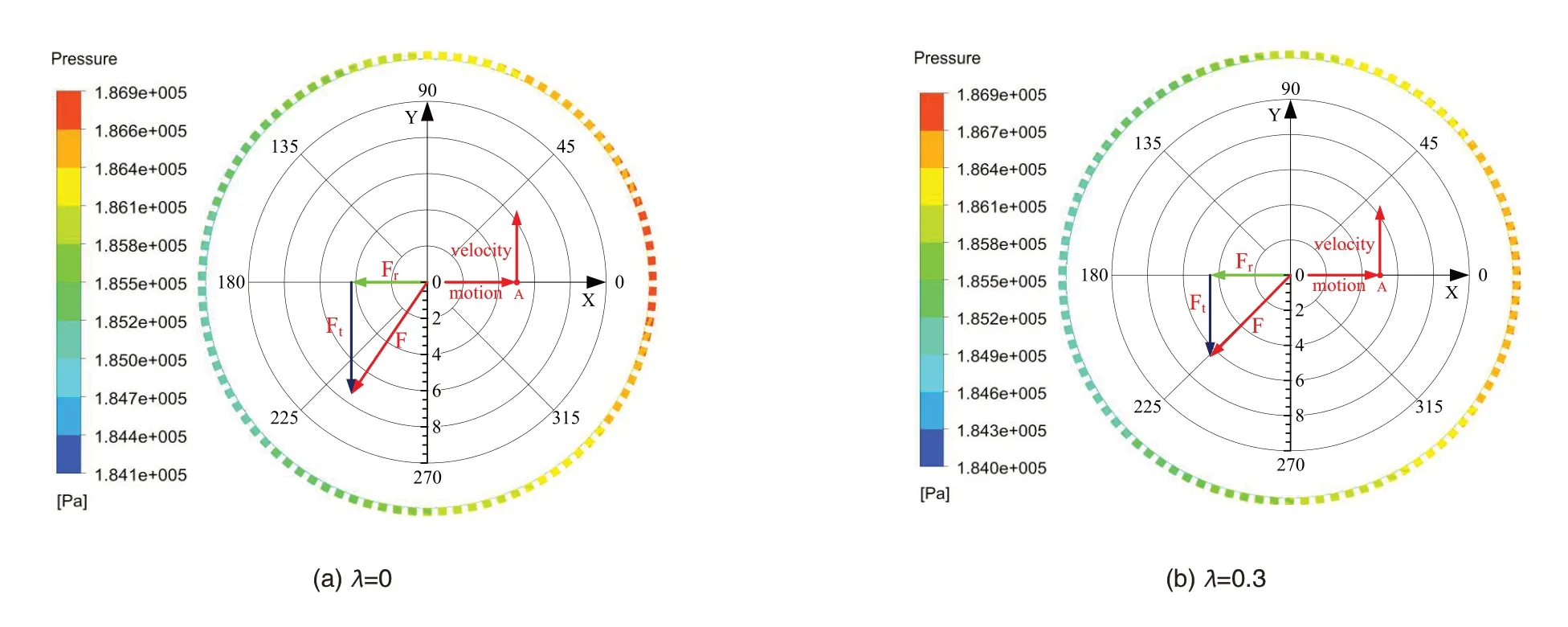
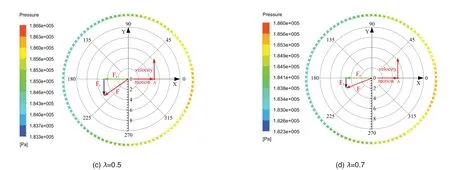
图12 四种预旋下密封腔室内压力分布云图Fig.12 Pressure distribution in seal chamber under different inlet pre-swirl ratios

从图13(a)、(b)、(c)和(d)中可以得出，随着涡动频率的增加，Cxx与Kxy减小，而Cxy与Kxx增大。在同一涡动频率下，随着预旋比的增大，Cxx与Cxy减小，而Kxx与Kxy增大。

图13(d)、(e)分别为涡动频率对蜂窝密封有效阻尼系数与有效刚度系数的影响。从图中可以看出，有效阻尼系数随着涡动频率的增加先增大后减小，有效刚度系数随着涡动频率的增大而增大。当涡动频率相同时，随着预旋比的增大，有效阻尼系数减小，有效刚度系数增大，转子稳定性降低。当涡动频率为160Hz，预旋比为0.3，0.5，0.7相比预旋比为0，有效阻尼系数分别降低了7.8%、16.7%与28.0%，直接阻尼系数分别降低了3.1%、8.7%与16.7%，交叉刚度系数分别降低了40.3%、64.2%与85.3%。因此可以分析得出随着预旋比的增大，有效阻尼系数减小主要是因为交叉刚度系数的增大，即进口预旋影响密封稳定性的机理为其会促使周向旋流增大，从而导致周向压力分布不均匀，密封稳定性降低。