面向变精度仿真数据建模分析的多任务学习方法比较研究＊

吴 锴 王晓放 边 超 刘海涛

（大连理工大学能源与动力学院）

0 引言

机器学习模型，又称代理模型，是一种数据驱动的学习预测模型，能够自动从数据中挖掘输入输出的非线性映射关系，实现对目标量的快速预测。相比于传统的单任务学习，多任务学习（multi-task learning，MTL）[1]是机器学习中一个极具前景的研究方向，其目标是利用多个相关或部分相关的学习任务中包含的共享信息来构建更准确的学习模型。

例如，Bonilla 等人提出了高斯过程（Gaussian process，GP）背景下的多任务学习，即多任务高斯过程（multi-task Gaussian process，MTGP）[2]，仅基于任务标签和每个任务的观察数据来学习任务间的依赖关系。Kennedy 和O’Hagan[3]提出的自回归Kriging 方法适用于多精度场景，在推断高精度模型时使用包含低精度模型的协方差，而这正是推导CoKriging 模型的依据。此外，根据Park和Harftka等人[4]的介绍，我们可以通过简单的数据融合框架将单精度模型组合成多精度模型，例如，基于 Kriging 模型的简单差异框架（simple discrepancyframe work by Kriging，SDK）是其中的典型代表。

多（单）任务学习模型在工程设计中的应用非常广泛。例如，冀春俊等[5]采用基于Kriging模型的遗传算法对压缩机离心叶轮轮盘形状优化设计，优化后的叶轮质量更轻，摩擦端面变形量更小。陈阳等[6]基于BP（Back-Propagation）神经网络构建了预测系列化轴流风机的效率和全压的学习模型，结果表明模型的预测值与实验值的一致性较好。刘佳雯等[7]提出了基于期望改进的Kriging模型来处理随机模糊和放大因子之间复杂的非线性关系，并以一个集总参数的叶片盘为例，说明该方法在精度上优于常用的多项式响应面法。KUYA 等[8]使用CoKriging 模型对机翼高度、攻角（自变量）和截面下压力（目标量）进行建模，分析地面效应下带涡发生器倒翼的气动性能，并探讨了不同取样方法对目标值误差的影响。陈梦羽等[9]提出一种利用BP 神经网络的多目标遗传算法，设计了一种自适应风机进气道畸变的翼型，减小了叶型损失及其对入射角的灵敏度。韩忠华等[10]通过Euler 数值模拟和RANS 数值模拟分别得到低精度和高精度样本，使用一种改进的CoKriging 模型对RAE2822 翼型性能进行预测分析。Bonfiglio等[11]使用多精度高斯过程回归和贝叶斯优化等机器学习工具，基于粘性仿真求解器来构建多精度预测框架，对超空化水翼的外形进行优化改进，结果使超空化水翼的性能得到了有效的提升。还有李增聪等[12]对多级加筋壳使用多精度模型，提高了对多级加筋壳后屈曲特性的预测精度并节约了计算成本。

从上述文献回顾可以发现，不同的多（单）任务模型在不同应用场景下各有优劣。因此有必要对比不同应用场景下典型多任务学习模型的表现，为多任务模型在工程机械设计分析中的应用提供一定的经验指导。

本文对比研究的多任务模型包括多任务高斯过程[2]、CoKriging 模型[13]以及SDK 模型[4]，并选择单任务的Kriging模型[13]作为对比基准。本文首先，基于典型的多精度数值算例对比不同模型的特点和表现；再针对实际的机翼翼型设计问题，将有关翼型气动系数的多精度数据视为“多任务”，通过共享多精度数据构建多任务学习模型以准确预测翼型气动系数。最后，给出本文的研究结论。

1 单（多）任务模型简介

1.1 Kriging模型

Kriging 模型发端于地质统计学，是一种依据协方差函数对随机过程或随机场进行空间建模和预测的回归算法。它能够在特定的随机过程中给出最优线性无偏估计（best linear unbiased prediction，BLUP）。若协方差函数的形式等价，且建模对象是平稳高斯过程，那么Kriging 等效于高斯过程回归（Gaussian process regression，GPR）[14]。

1.2 MTGP模型

高斯过程是一种随机过程，代表一系列服从正态分布的随机变量在一指数集内的组合。高斯过程由其数学期望和协方差函数完全确定，并继承了正态分布的诸多性质。而多任务高斯过程同时对多个相关变量进行高斯过程建模，由此产生的多任务模型可以学习多个信号之间的相关性，共享多个变量的信息，从而提高建模精度。

给出训练样本集X，定义M个任务的响应集y=(y11,…,yN1,…,y12,…,yN2,…,y1M,…,yNM)T，其中是指第l个任务在第i个点x(i)上的响应。

这里为了叙述方便，假设各任务的训练样本集x一样。但是注意，MTGP 模型允许各任务的训练样本集{ Xi}1≤i≤m不一样。

给定M个任务的训练数据{X,y}，以学习各任务的关联性以实现跨任务知识共享和迁移[2]。因此，MTGP 模型使用如下交叉核函数来表征各任务之间的相关性。

其中，表示任务l和任务j之间的相似性；k*是各输入之间的协方差函数。可以进一步提高MTGP 模型的表达能力，包括使用更多的潜函数来捕捉不同尺度的特征[15]，叠加任务特有的潜函数以降低负迁移[16]，使用卷积过程构造更强大的多任务核函数[17]等。

MTGP 模型一个非常重要的特征是它没有考虑多精度数据的非对称性[18]。如果假设各个任务是有序的，那么半正定矩阵就需要构建一个块对角化的结构，如下文介绍的CoKriging模型。

1.3 CoKriging模型

CoKriging 模型可以视为多精度场景下MTGP 模型的扩展。MTGP模型假设各任务同等重要，这显然与多精度数据的特点不匹配。因此，CoKriging 模型特别考虑了多精度数据的非对称性，重点提高高精度模型的预测精度。本文考虑使用高/低两个精度级别构建的CoKriging 模型[13]。假设Xe和Xc分别代表高低精度样本点，构成样本集

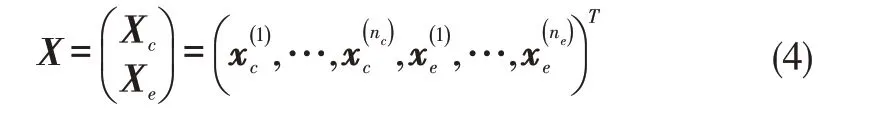
特别地，一般认为高精度样本是低精度样本的子集Xe⊂Xc，这种情况可以解耦CoKriging 模型，降低计算复杂度[19]。此外，Ye和Yc分别是Xe和Xc对应的目标函数值，构成响应值的集合

CoKrigng模型可以表达为

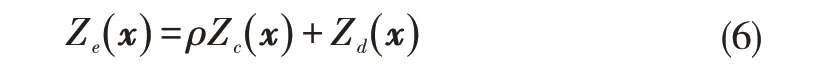
其中，Ze(·) 和Zc(·) 分别表示高低精度对应的高斯过程，ρ是缩放因子，Zd(·) 表示残差高斯过程。类似于Kriging 模型对协方差的构建，CoKriging 模型需要构建各精度高斯过程之间的协方差，完整表示为

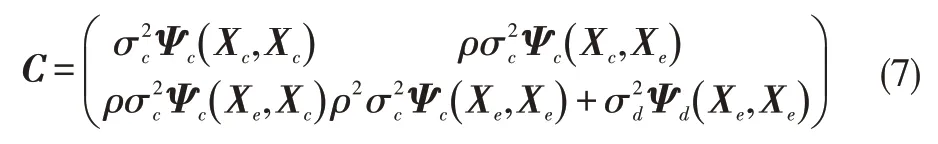
其中Ψc是指用低精度核函数刻画的样本点之间的相关矩阵，Ψd表示用残差核函数刻画的相关矩阵。我们一般需要通过最大似然估计（maximum likelihood estimate，MLE）得到超参数θc，θd，pc，pd以及缩放因子ρ。

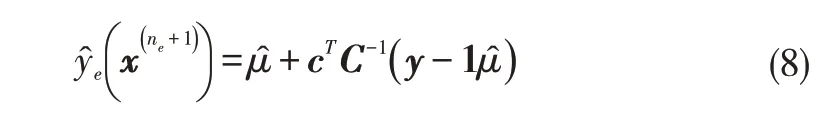
注意CoKriging的预测表达式包含高精度预测和低精度预测两部分，一般会更关心高精度的数据，故上式给出的是CoKriging的高精度预测，其中

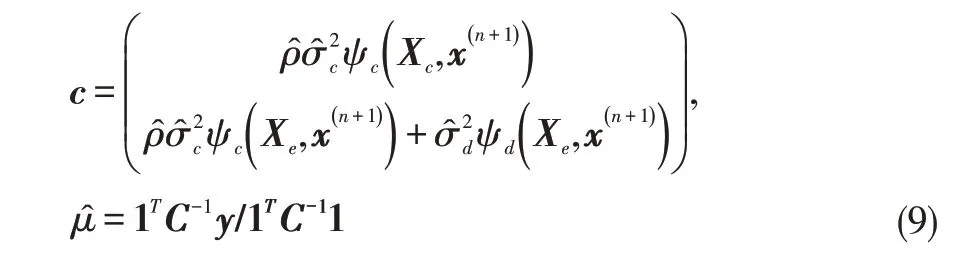
1.4 基于Kriging模型的简单差异框架

SDK模型借助桥函数[20](x) 构造多精度模型，表达式为

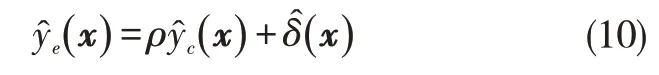
其中，(x)表示使用低精度样本集构建的Kriging模型在点x 处的预测值；(x)表示点x 处高低精度响应的残差预测值；ρ为缩放因子，用于最小化高精度样本值(x)与低精度替代项(x)的差异。注意，为了构建残差模型(.)，需要先在高低精度样本的公共点计算残差δ(xcom)

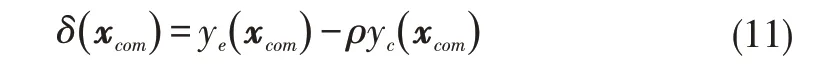
其中，xcom∈Xcom=Xe∩Xc是高低精度样本公共点，ye(xcom)和yc(xcom)分别是公共点处的高低精度样本值。所有δ(xcom)构成差值集Δ(Xcom)，通过Xcom和Δ(Xcom)构建Kriging模型(·) 。

2 数值算例

本节首先在一个一维多精度数值算例和一个六维多精度数值算例上比较分析了多（单）任务模型的特点和表现，然后将它们应用到一个真实的翼型升阻力系数多精度预测分析问题。注意，考虑到计算复杂度，这里我们使用只有一个潜函数的MTGP模型[2]。

2.1 一维数值算例

本算例将不同的代理模型应用于一维数值函数的预测。使用的高精度函数为fe(x)=(6x-2)2sin(12x-4)，x∈[0,1]，低精度函数为fc(x)=Afe+B(x-0.5) -C，其中A=0.5，B=10，C=5 以近似高精度函数[21]。在fe的定义域[ 0,1]上每隔0.05 取一个点，共20 个点作为低精度样本，为降低CoKriging模型的计算复杂度，令高精度样本是低精度样本子集，选定高精度样本集Xe={0,0.4,0.6,1} 。另外，在定义域[0,1]上每隔0.01取一个点作为测试集，共100个点。其中单任务的Kriging模型仅通过高精度样本集建模预测，而多任务模型将使用高低精度样本集协同预测，以验证多任务学习共享知识提高预测精度的特点。

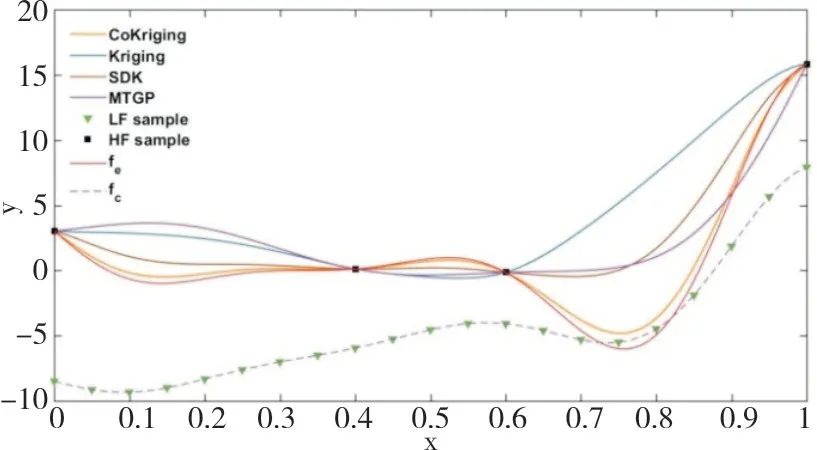
图1 四种模型的预测结果对比Fig.1 Comparison of prediction results of the four models

表1 不同模型预测误差Tab.1 RMSE results of different model

根据图1和表1的比较结果，可以发现Kriging模型预测误差较多任务模型明显更大，证明了多任务学习共享知识以提高预测精度的能力。CoKriging模型几乎捕捉了高精度函数的所有特征，误差最小；MTGP 模型预测误差较大，推测是由于MTGP模型建模时没有考虑多精度数据的非对称性，没能对高精度模型进行更为准确的预测；而SDK 模型较大的预测误差是由于其建模时分别构造高低精度模型和残差模型，没有考虑三者的相互关系，对多精度信息利用不足。

2.2 基于hartmann六维函数的数值算例

本节针对多任务模型，一方面研究当样本扩充到高维，样本数据量较大时，各模型的预测效果；另一方面研究高低精度样本数对模型预测误差的影响。为便于叙述，这里将多任务学习中获取一组高低精度样本所需的总成本称为总预算，用高精度点数表示为ntotal；定义成本比（cost ratio，cr）为一个高精度样本的计算开销对应cr个低精度样本的计算开销；定义高精度样本数ne和低精度样本数nc之比为尺寸比（size ratio，sr）[4]。其中成本比、总预算与高低精度样本数的关系为

尺寸比与高低精度样本数的关系为

为降低CoKriging 模型的计算复杂度，样本选取原则与一维算例一致，即高精度样本集是低精度样本集的子集。为达到均匀取点的目的，采用拉丁超立方抽样和最近邻抽样相结合[22]的采样策略。选用定义在[0.1,1]6上的hartmann六维函数作为高精度函数，其表达式如下：

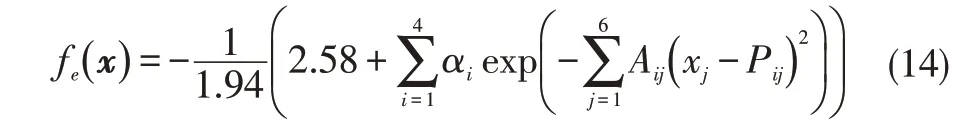
其中α={1 1.2 3 3.2}T为函数参数，A和P为常数矩阵

使用hartmann 六维函数的近似函数作为低精度函数：

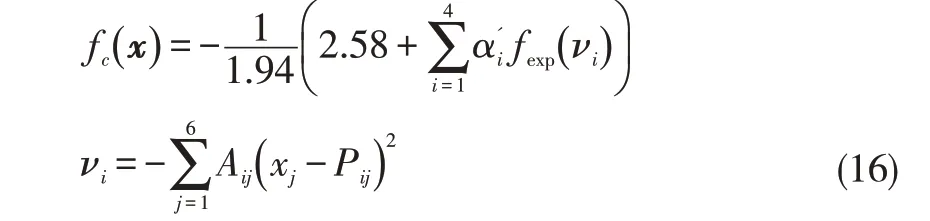
其中，={0.5 0.5 2.0 4.0}T为函数参数，fexp(x)是由指数函数构成的近似函数，

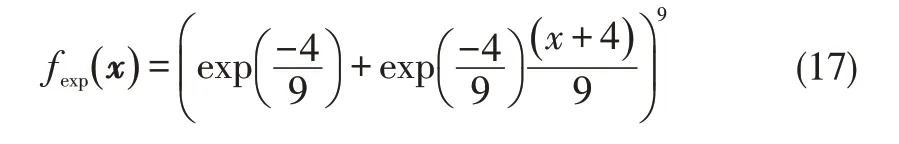
本算例固定总预算为28，成本比为30，在对比不同模型预测误差的同时研究均方根误差（root mean square error，RMSE）随尺寸比的变化关系。选取ne∈[3,23]，取值间隔2，共计11个不同的高精度样本数（即11个尺寸比值），而低精度样本数随高精度样本数而变化，如式(12)。

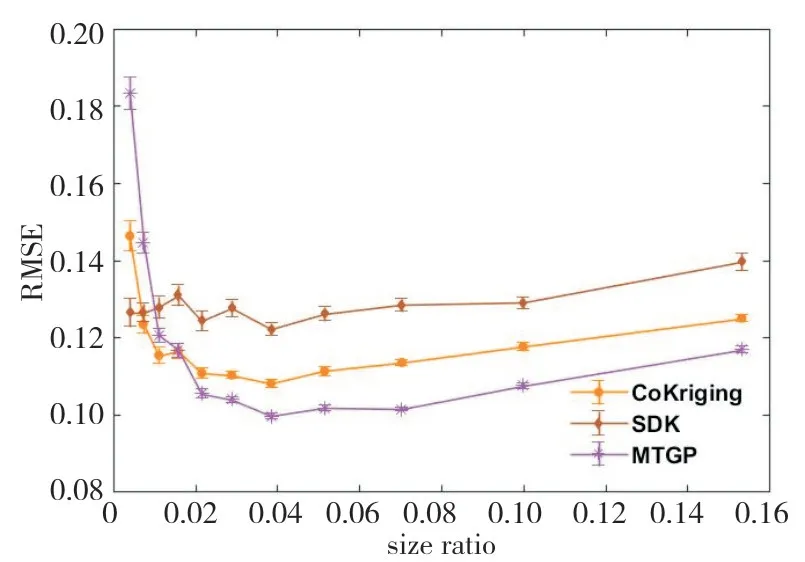
图2 在hartmann函数上各模型预测误差随尺寸比变化的误差棒图Fig.2 An error bar diagram of different models with size ratio on the hartmann case

如图2 所示，1）MTGP 和CoKriging 预测的RMSE 随尺寸比呈现先减小后增加的趋势，尺寸比过大或过小都会影响其预测精度，在尺寸比为0.03～0.07的范围内，预测误差普遍较小；2）当尺寸比大于0.01 时，MTGP 表现最优，SDK 模型表现最差，说明在hartmann 六维函数场景的大多数尺寸比范围内，MTGP模型在几种模型中最为准确。当尺寸比小于0.01时，MTGP模型误差上升剧烈，说明高精度数据的减少对MTGP 预测的影响很大；3）SDK 模型预测的RMSE 最大，且尺寸比对SDK 模型的影响弱于对MTGP 和CoKriging 的影响，可能是由于其线性加和的建模方式对多精度信息不够敏感。但结果依然呈现出误差随尺寸比增加而逐渐变大的趋势，证明高精度点过多会降低SDK模型预测的准确性。

3 基于RAE2822翼型仿真的多任务学习

本节将MTGP 和CoKriging 模型应用于RAE2822 翼型气动系数的预测，并将仅使用高精度样本训练的单任务Kriging模型作为对比基准。

3.1 翼型空气动力系数

根据翼型理论，翼型的空气动力系数主要用于衡量翼型的气动性能[23]，包括升力系数Cl，阻力系数Cd以及力矩系数Cm。将其作为多任务学习的目标量，训练数据集通过fluent翼型仿真计算获得。假设Lift是翼型所受升力，Drag是翼型所受阻力，来流速度为u∞，翼型攻角为αA，翼型弦长为c，机翼（或叶片）受力面积为S，空气密度为ρ∞，那么翼型的升力系数定义为

翼型的阻力系数定义为

图3 翼型力矩系数计算示意图[24]Fig.3 Schematic diagram of airfoil moment coefficient calculation

如图3所示，将升阻力的作用点固定在0.25c处，由于阻力沿弦长方向，故不会产生力矩，此时便只增加了升力从压力中心平移到该点的附加力矩M，将翼型的力矩系数定义为

3.2 可靠性验证

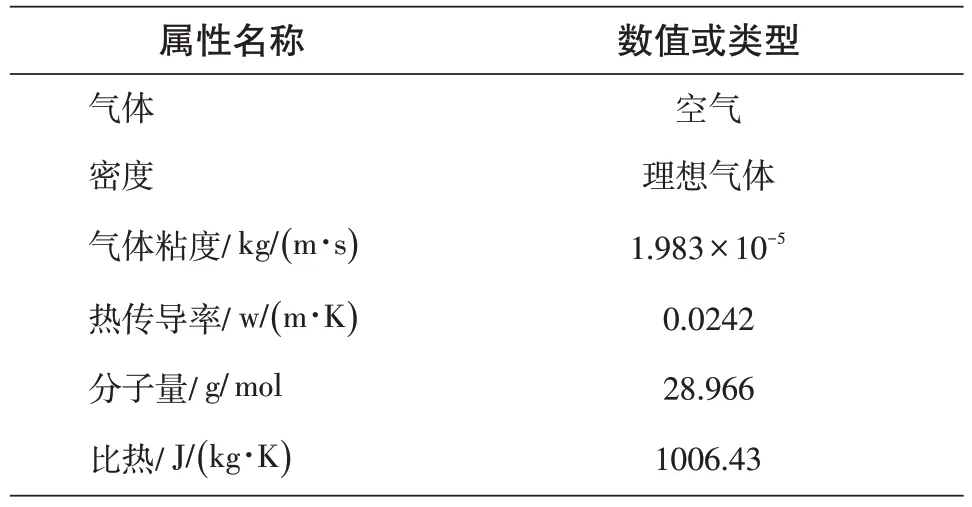
表2 介质属性Tab.2 Dielectric properties

为校验fluent 仿真所得气动系数的准确性，我们将RAE2822气动系数的仿真结果与实验值[25]比对。fluent翼型仿真包括建模、划分网格、求解、后处理四个步骤[26]。仿真的几何模型及网格如图4和5所示。仿真的介质属性及边界条件如表2和表3所示。

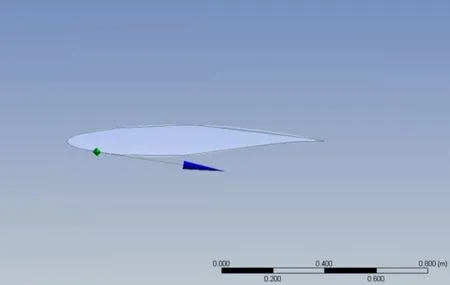
图4 翼型建模图Fig.4 The geometry model of studied airfoil

图5 机翼仿真模型网格划分（网格数42234）Fig.5 The meshes for computational model of airfoil(the number of meshes is 42234)

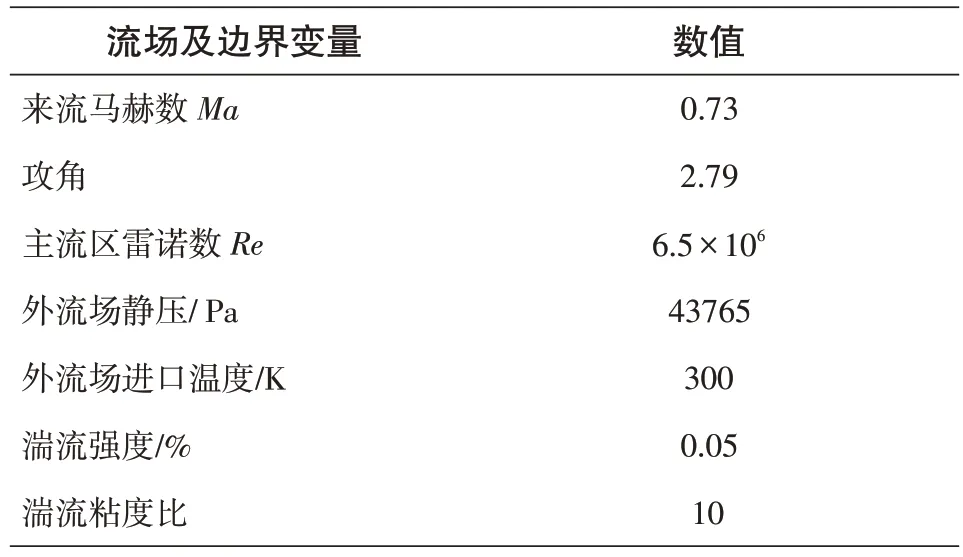
表3 流场及边界条件Tab.3 Flow field and boundary conditions

机翼仿真模型求解部分选择基于N-S方程的k-ω湍流模型。相比于常用的Spalart-Allmaras 模型，它在预测边界层特征的细节方面更加准确。

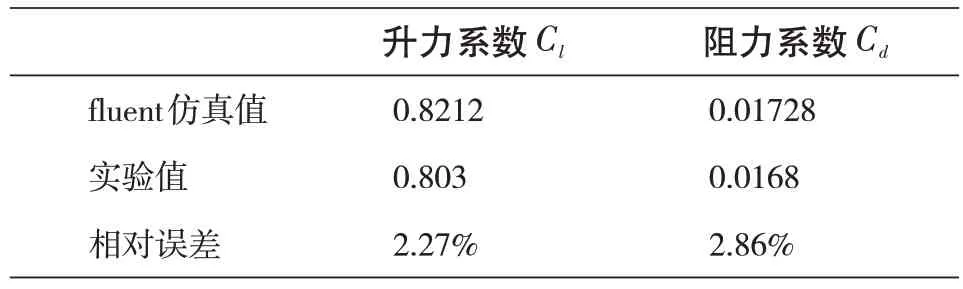
表4 翼型气动系数仿真值与实验值对比表Tab.4 Comparison of airfoil simulation results and experimental results

如表4 所示，Cl和Cd的仿真值相对于实验值的误差均小于3%。说明fluent翼型仿真具有较高的可靠度，可以通过fluent翼型仿真生成代理模型的训练集。

3.3 网格无关性验证

本实验中多任务模型所使用的高低精度样本均是通过fluent 仿真获得的，而样本数据高低精度的区别依赖于网格数。如表5 所示，在一定网格数的范围内，翼型气动系数的仿真误差随网格数的增加（即网格分辨率的提高）而降低，当网格数达到某一平台阶段时，仿真误差将不受网格分辨率的影响，此时即达到网格无关。

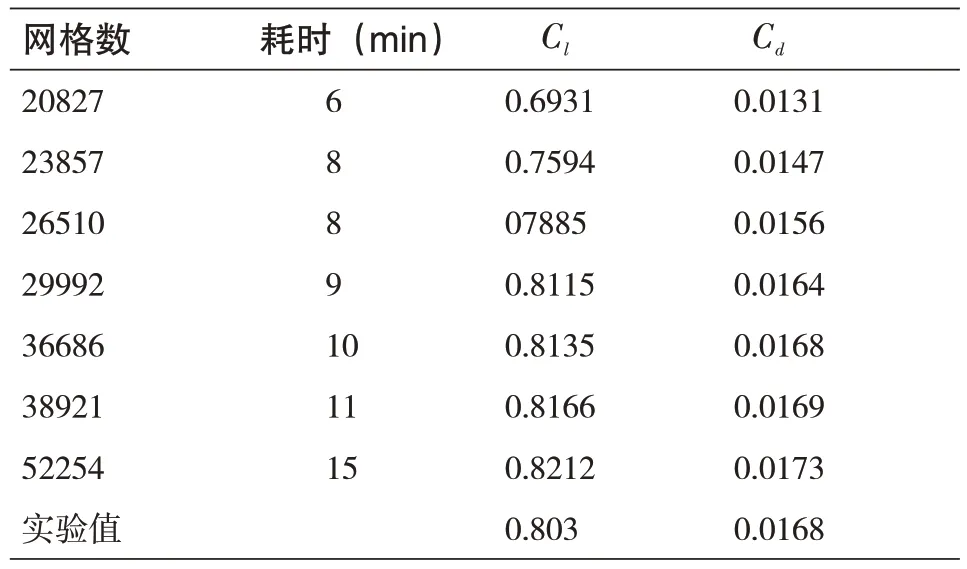
表5 翼型仿真的网格无关性验证Tab.5 Mesh independence verification of airfoil simulation

根据以上网格无关性验证的结果，选取生成低精度数据的模型网格数为20827，生成高精度数据的模型网格数为52254。

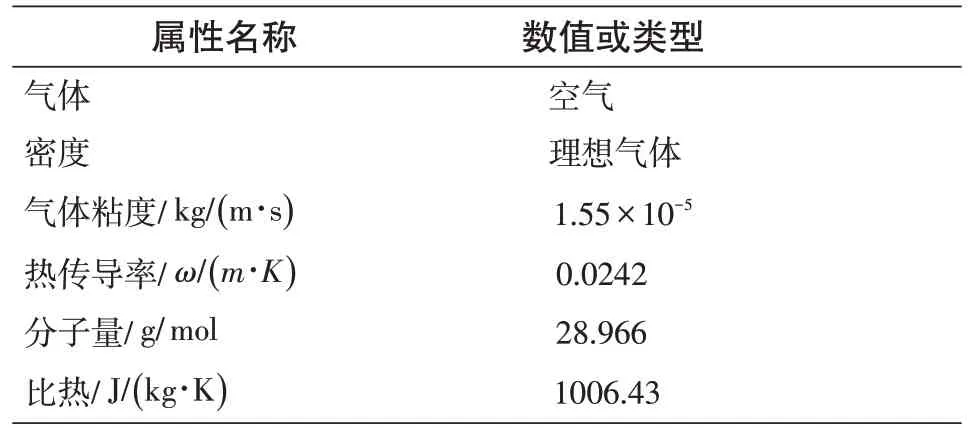
表6 介质属性Tab.6 Dielectric properties

表7 流场及边界条件Tab.7 Flow field and boundary conditions

3.4 单变量模型预测实验及结果分析

本实验固定Ma不变，研究翼型升阻力系数随攻角的变化情况。仿真模拟工况为6500m左右高空，空气温度为-27℃，大气压力为43765Pa，介质属性、流场及边界条件如下：

图6 翼型升力系数随攻角变化曲线Fig.6 The variation curve of the lift coefficient of airfoil with the angle of attack

图7 翼型阻力系数随攻角变化曲线Fig.7 The drag coefficient of airfoil varies with the angle of attack

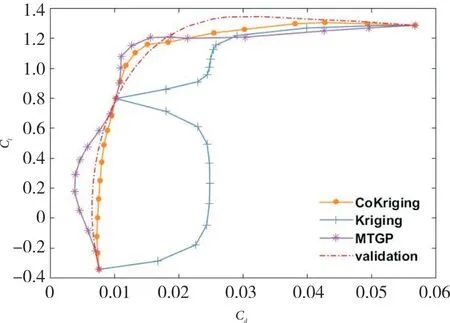
图8 翼型升阻力系数曲线Fig.8 Polar curve of airfoil

确定Ma=0.2，攻角作为变量，其低精度样本在[-5°，15°]上每隔1°取点，高精度样本取{-5°，5°，15°}，并将25 个低精度点作为测试集，验证集通过高分辨率网格仿真计算得到。另外查阅资料[10]显示，攻角较大时，升力系数会出现下降，所以在αA∈[11°，15°]上密集取点（间隔0.5°）以捕捉这一特征。

如图6 所示，三种模型均捕捉到了Cl随αA的上升过程，但多精度模型（尤其是CoKriging 模型）更加接近验证曲线，且捕捉了上升曲线末尾的平缓段。图7中多精度模型的预测值与验证值几乎一样，而Kriging 模型则出现了较大误差。这是因为训练集只有三个高精度点，影响了单精度模型的预测精度。图8中多精度模型（尤其是CoKriging 模型）的预测曲线同样远远优于Kriging 模型的预测曲线，只是对Cl峰值的预测出现了一定偏差。可以发现，上述所有实验结果中，CoKriging模型预测精度均优于MTGP 模型。这是因为MTGP 在建模时未考虑多精度数据的非对称性，因此其高精度预测略差于CoKriging模型。

3.5 双变量模型预测实验及结果分析

图9 不同模型预测的升力系数随攻角和马赫数的变化Fig.9 The lift coefficients predicted by different models with the angle of attack and Mach number

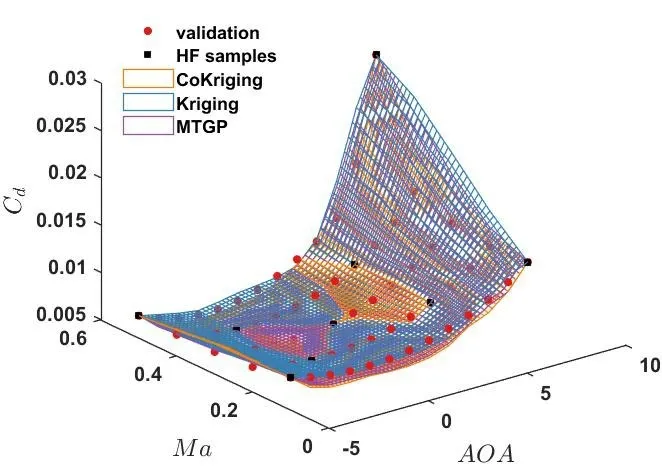
图10 不同模型预测的阻力系数随攻角和马赫数的变化Fig.10 The drag coefficients predicted by different models with the angle of attack and Mach number

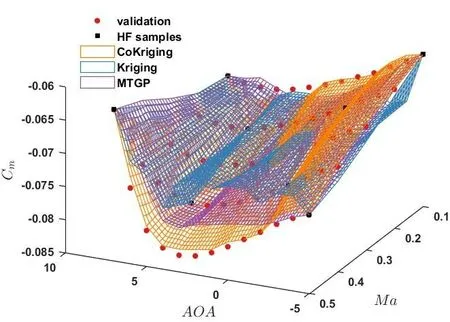
图11 不同模型预测的力矩系数随攻角和马赫数的变化Fig.11 The moment coefficients predicted by different models with the angle of attack and Mach number

本实验考虑两个自变量，即来流马赫数和攻角，其介质属性、流场及边界条件同单变量实验，目标量中加入力矩系数Cm。如图9 所示，在Ma∈[0.1，0.5]且αA∈[-5°，7°]的范围内采用网格法取低精度样本，共计nL=65，均匀取点以利于两种模型预测的准确度；高精度样本作为低精度样本的子集，从低精度样本中均匀选取nH=9 个样本。测试集的攻角和马赫数与低精度样本一致，验证集通过高分辨率网格仿真计算得到。

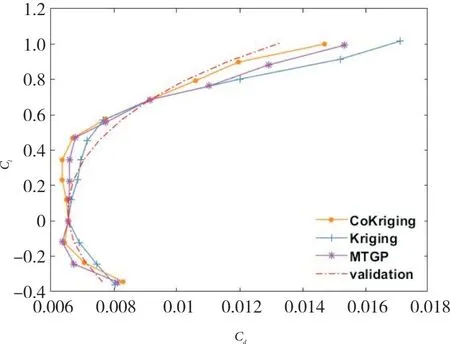
图12 Ma=0.2时升阻力系数曲线对比Fig.12 Comparison of the polar curves when Ma=0.2

图13 Ma=0.2时力矩系数随攻角的变化Fig.13 The change of moment coefficient with the angle of attack when Ma=0.2

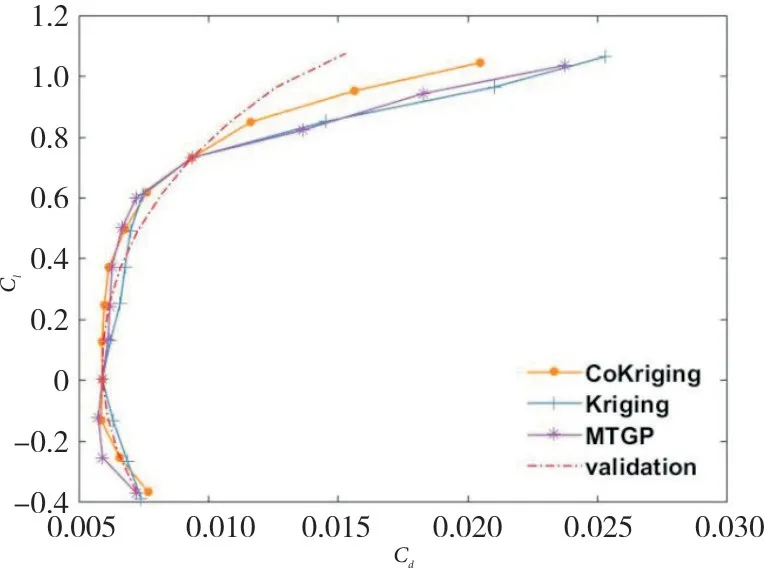
图14 Ma=0.4时升阻力系数曲线对比Fig.14 Comparison of the polar curves when Ma=0.4

图15 Ma=0.4时力矩系数随攻角的变化Fig.15 The change of moment coefficient with the angle of attack when Ma=0.4

图9 和图10 所示是各模型预测的Cl和Cd随αA的变化，可以发现对于这两个气动系数，各模型的预测结果差异不大；图11 对比各模型对Cm的预测情况，CoKriging 模型更好地预测了Cm变化的波谷，MTGP 模型次之，而Kriging 模型预测情况较差，只预测出Cm的小幅波动。

图16 AOA=-3°时升阻力系数曲线对比Fig.16 Comparison of the polar curves when AOA=-3°

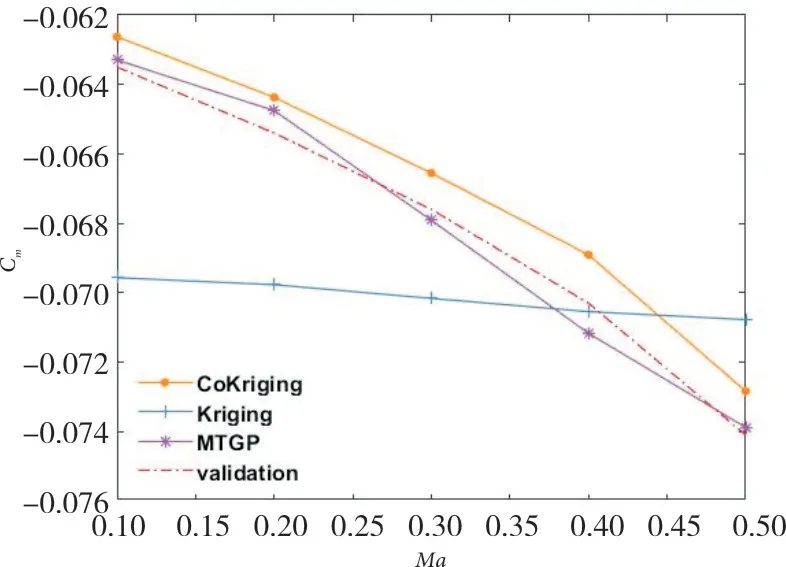
图17 AOA=-3°时力矩系数随攻角的变化Fig.17 The change of moment coefficient with the Mach number when AOA=-3°

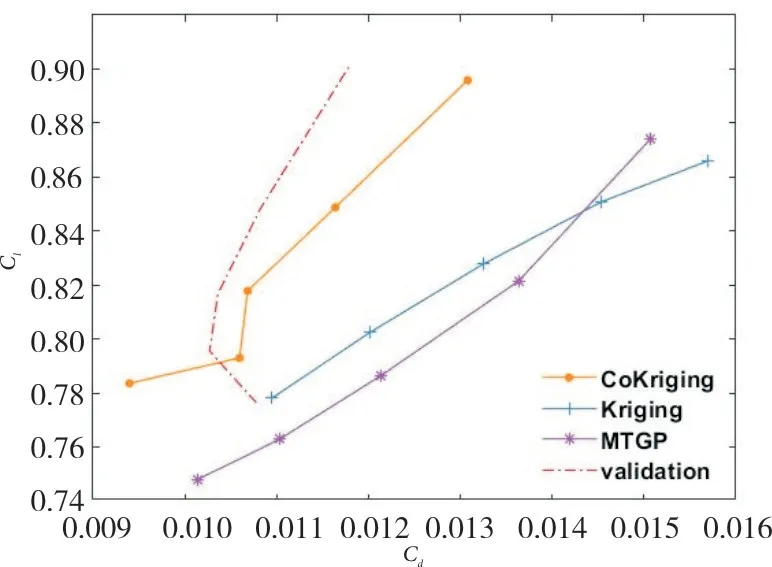
图18 AOA=5°时升阻力系数曲线对比Fig.18 Comparison of the polar curves when AOA=5°

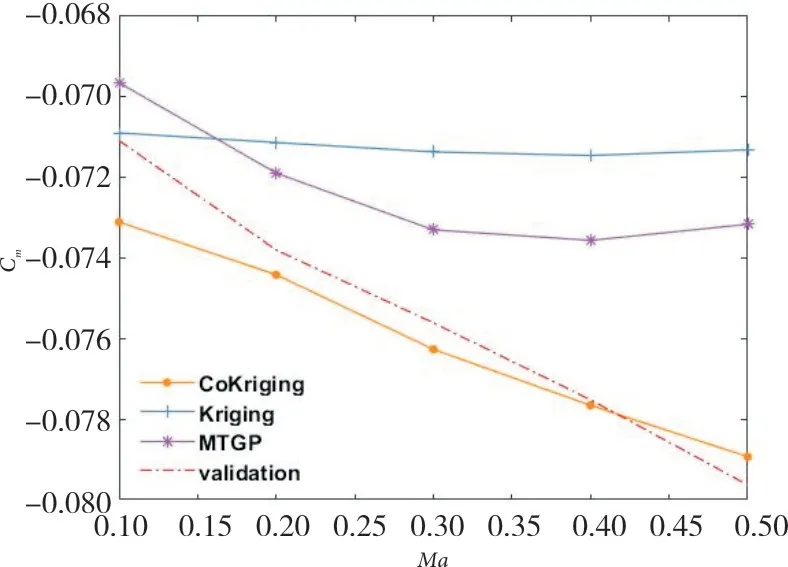
图19 AOA=5°时力矩系数随攻角的变化Fig.19 The change of moment coefficient with the Mach number when AOA=5°

更进一步，图12～15 分别截取Ma=0.2 和Ma=0.4时的片层图。通过图12 可以观察到，三种模型对升阻力系数的预测在不同取值段各有优劣；图13 反映出MTGP和CoKriging模型预测结果相近且更接近验证值；图14显示MTGP模型和Kriging模型对升阻力系数的预测接近，但精度较差，而CoKriging模型的预测结果最接近验证值；图15 直观地表明CoKriging 模型对力矩系数有更强的预测能力，MTGP 模型次之，Kriging 模型没能得到较好的预测结果。

图16～19分别截取攻角为-3°和5°时的片层图。图16 和图18 反应出CoKriging 模型对升阻力系数曲线的近似总体更为准确，MTGP 和kriging 模型近似误差较大。图17的结果与之前稍有不同，MTGP模型的预测结果最为准确，CoKriging 模型误差稍大，kriging 模型预测误差最大。图19依然表明CoKriging模型的预测最为准确，MTGP 模型次之，单精度的kriging 模型预测误差最大。

可见，多精度模型借助关联的低精度数据的确能够提高高精度模型预测质量。在上述双变量实验结果中，CoKriging 模型预测精度总体上优于MTGP 模型，同样是因为MTGP 处理多精度数据时采用的对称结构与数据特征不匹配。

4 结论

本文通过多精度实验充分对比分析了MTGP、CoKriging和SDK三种多任务模型以及单任务Kriging模型的特点及预测性能。比较结果表明，虽然各模型的预测结果受到成本比、尺寸比等样本条件的影响，但无论是数值算例还是对翼型气动系数的预测，都表明多精度模型能够借助相关联的便宜、丰富的低精度数据提高对昂贵的高精度目标的预测质量。在工程实践中，如果只有少量的高精度数据，那么我们可以通过仿真等手段获取充足的低精度数据，应用多任务学习方法提高对目标量的预测精度。

在多数实验结果中，CoKriging 对高精度目标的预测结果更好，是因为1）SDK 模型线性加和的简单解耦建模方式未能捕捉充分的多精度关联信息，2）MTGP模型在使用多精度数据时采取的对称结构未能对高精度模型做更好的预测。但是，hartmann 六维函数中MTGP的优异表现说明不同多任务模型在不同场景下预测效果各有优劣。因此，在实际应用中，选用哪一种多任务模型还需考虑问题本身的特点。