考虑一致性约束的车辆路径问题综述

李路遥，沈一帆，夏 俊，沈海辉

考虑一致性约束的车辆路径问题综述

李路遥，沈一帆，夏 俊，沈海辉

(上海交通大学，中美物流研究院，上海 200030)

车辆路径问题是物流和交通运输领域的研究热点。近年来，为应对激烈的市场竞争，越来越多的企业开始关注如何在降低成本的同时保证服务效率和服务质量。实践表明提高车辆路径方案的一致性不仅可以提高服务效率，还能显著提高客户满意度。因此，考虑一致性约束的车辆路径问题(又称一致性车辆路径问题)应运而生。一致性车辆路径问题是相对较新的车辆路径问题变种，相关成果具有重要的实践和学术价值。随着多样化一致性约束的提出以及相关数学模型和优化方法的迭代更新，目前针对一致性车辆路径问题已有一定数量的研究积累。本文从车辆路径问题的分类、一致性车辆路径问题的背景介绍、模型、求解算法等方面对该问题进行了综述。在一致性车辆路径问题中，一致性约束主要有时间一致性、人员一致性和路线一致性要求。时间一致性和人员一致性约束较为常见，路线一致性约束则相对更为新颖。一致性车辆路径问题的求解方法以启发式算法为主，尤其是大、中型实例(时间周期5d，客户数量50以上)的求解；而部分精确式算法对中小型实例(时间周期3～5d，客户数量50及以下)也展现了良好的性能。

物流工程；一致性车辆路径问题；时间一致性；人员一致性；路径一致性；文献综述

0 引 言

随着物流行业的不断发展，物流业对国民生产总值的贡献程度越来越大，作为“第三利润源”的物流业也受到越来越广泛的关注。面对激烈的市场竞争，如何降本增效是物流企业持续关注的问题。在物流运输中，燃油消耗是主要的成本。车辆路径问题(Vehicle Routing Problem，VRP)的目的就是在满足运输要求的前提下缩短车辆总行驶距离，以达到节约运输成本的效果。这不仅可以节约成本、增加利润，还可以减少尾气排放，提升客户满意度。因此，VRP一直是物流服务领域研究的热点问题。

VRP最早由Dantzig和Ramser[1]于1959年提出，其目的是在满足服务需求约束的前提下，寻找到最优路线或近似最优路线。经典VRP可以简述为：已知一个配送起点和若干客户需求点的位置和两点之间的距离，在满足车辆容积约束和所有客户需求的条件下，求解出一条距离最短的车辆行驶路径。随着实际需求的不断变化，各种变种VRP层出不穷，较为常见的VRP变种问题有以下几大类：

(1)有装载约束的车辆路径问题。装载约束是车辆路径问题中最关键的因素之一，在实际应用中也最为常见。主要的装载约束有车辆容积约束、装载方式约束。有车辆容积约束的车辆路径问题可分为容积限制的车辆路径问题(CapacitatedVehicle Routing Problem，CVRP)、多车型车队的车辆路径问题(Heterogeneous Fleet Vehicle Routing Problem，HFVRP)和甩挂运输车辆路径问题(Truck and Trailer Vehicle Routing Problem，TTVRP)。CVRP的约束中，车辆的类型和容积都是相同的[2]，但是在实际问题中，运输企业的车辆并不一定完全相同，因此有了HFVRP。不同于CVRP，HFVRP拥有不同容积和使用成本的车型[3]。随着实际情况的变化，有些企业的货物是通过甩挂运输的方式为客户进行配送[4]，因此有了TTVRP。装载方式约束主要是指在车辆路径问题中，货物的装箱方式、装箱顺序和方向有一定的要求。例如二维装载车辆路径问题(Vehicle Routing Problem with Two-dimensional Loading Constraints, 2L-CVRP)不仅要规划车辆路线，还要考虑货物的长度和宽度限制。根据货物的装箱顺序和方向要求，也可以将其作为问题的约束，于是出现了有方向的2L-CVRP[5]等变种问题。除此之外，在实际问题中，部分货物尤其是易碎品的运输需要考虑货物的高度或堆叠问题，例如家电在运输过程中需要利用厢式货车运输并遵循“不可堆叠”或“重不压轻”的原则，三维装载车辆路径问题[6]应运而生(Vehicle Routing Problem with Three-dimensional Loading Constraints, 3L-CVRP)。

(2)同时取送货的车辆路径问题。经典的VRP要求车辆完成配送后返回出发地即可，但在实际运营中，货物交付并不完全意味着运输过程的完成，客户的退换货、邮件收取等业务还要求配送车辆在送货后完成取货的过程。因此，出现了同时取送货的车辆路径问题(VRP with Simultaneous Pickups and Deliveries, VRPSPD)。VRPSPD要求车辆在为客户配送货物的过程中同时收取客户的退货或是邮件并装入车辆后返回出发地[7]。

(3)带时间窗的车辆路径问题。带时间窗的车辆路径问题(VRP with Time Windows, VRPTW)十分常见，即客户希望在某一时段中收到货物，运输车辆需要在该时段内到达配送点。VRPTW又可以分为带硬时间窗的VRP和带软时间窗的VRP。硬时间窗要求车辆不能晚于时间窗结束的时间到达，如果到达过早需要等待[8]；软时间窗对时间窗的约束有了一定的松弛，允许车辆迟到，但是车辆迟到需要付出额外的成本[9]。

(4)周期性车辆路径问题。周期性车辆路径问题(Period Vehicle Routing Problem, PVRP)是指在服务周期内，客户可能需要多天的服务，因此公司会生成几天的路线来拜访已知服务频率的客户[10]，即针对一段时期内的固定订单制定配送计划，目标是使得车辆总行驶距离最小。PVRP最早由Beltrami和Bodin[11]于1974年提出，其最初目的是解决城市垃圾车辆的路径规划问题，后来PVRP广泛应用于一些有固定服务需求的问题，例如快递配送、电梯的保养和维修、自动售货机和便利店补货[12]等。

除了上述四类常见的VRP变种问题外，还有诸如动态VRP、开放式VRP、多级VRP、绿色VRP[13]等问题。本文讨论的一致性车辆路径问题(Consistent Vehicle Routing Problem, ConVRP)属于考虑服务水平和客户满意度的周期性VRP，其中一致性要求是指在一定周期内的服务水平需要保持一致，例如在多天的服务周期内，同一司机需要大约在每个服务日的同一时间段内拜访同一个客户[14]。ConVRP是由CVRP和PVRP扩展而来[15]，部分ConVRP中也增加了时间窗约束或是同时取送货约束。与PVRP类似，ConVRP也是在一定时期内的多次规划，不同点在于PVRP重点是成本最低，ConVRP重点在于一致性要求，当关注重点不同时，整体方法会产生不一致的路线安排[16]。

1 一致性车辆路径问题背景介绍

一致性车辆路径问题最早由Groër等[14]于2009年提出，其出现源于快递公司和小件物流公司对客户服务水平的关注。2000年以来，国际快递物流公司逐渐将重点从以车队为中心转移到以客户为中心，通过提升客户满意度以增加每个客户的终身价值。在周期性车辆路径问题中，客户满意度是持续服务的结果，要求一定周期内服务水平的一致性。例如，一些小件物流公司的实践表明，提供一致的服务比节省1%～3%的运输成本更为重要[14]。以UPS为例，其司机通常会在一条固定的路线上工作很多年，司机与客户间存在密切联系[17]。在此基础上，早在2007年，UPS就已正式提供一致性服务，使得司机可以维护良好的客户关系，在配送同时能收集客户周围的业务信息或销售线索，产生额外的收益，这为公司带来了巨大的经济效益[14]。从此，一致性车辆路径问题逐渐进入人们视野。

所有ConVRP描述基本相似，即一组司机在多个时间段内访问同一组客户，目标通常是一致性要求下的运输成本最小。该操作过程也会受到车辆容积、有限的时间窗、有限工作人员等条件的约束。每天的输入参数是波动的，例如客户只需要一定周期内某些天的服务，因此需求每天都在变化。应对每天变化的需求，最简单的方法是每天都重新优化路线。然而，这种方法实际并不可行，因为一方面，公司需要每天获取客户数据，在很短的时间内计算新的路线，并将路线转发给司机，这个过程工作量较大、对计算效率要求高；另一方面，司机面对每天不同的路线，学习负担重，容易降低服务质量。因此不能单纯地将每天优化路线作为解决此类问题的办法，针对ConVRP设计专门的方法就显得尤为重要。

1.1 ConVRP应用场景

ConVRP在实际中有很多应用场景，主要有以下几类：

(1)快递配送中的一致性。近年来随着电商行业的迅速发展，包裹量激增，快递行业也迎来了快速发展时期。在激烈的市场竞争中，不少快递公司选择采用“价格战”的方式抢占市场份额。然而除了价格优势外，快递公司在市场竞争的另一关键因素是服务质量。2008年，Richard[18]调研发现，快递配送及小件物流与其他运输的主要区别在于对服务一致性的要求。经常需要快递服务的客户希望每天能在大致相同的时间被拜访，因此一致性高的服务可以改善客户关系；并且更高的客户满意度和司机对区域和客户的熟悉程度带来的经济效益会抵消因一致性而产生的更高的路线成本。例如快递行业巨头UPS在2003年就开始斥巨资研发可以提高一致性水平的路线规划系统，尽管该系统部署成本超过2.95亿美元，但是预计每年将为UPS节省3至4亿美元，同时每年可以减少10万t二氧化碳排放[19]。

(2)家庭护理中的一致性。随着老龄化加剧及综合医院服务模式的转变，卫生保健从形式固定的保健护理(如疗养院等)转向家庭护理。家庭护理服务使病人能够尽可能自主地住在家里，同时由熟练的工作人员进行探视和支持。通常，这项服务包括家政、送餐上门和医疗保健等[20]。医护服务人员通常将护理连续性视为质量目标[21]，服务人员应熟悉客户的习惯、特点及身体状况。因此，人员一致性简化了相关人员的沟通和交接，可以显著提高家庭护理的服务质量。

(3)供应商库存管理中的一致性。在供应商库存管理中，补货订单的时间和数量从由客户决策转变为由供应商决策。对供应商而言，面对激烈的市场竞争，单纯关注成本已经不足以满足客户需求，Coelho等[16]在IRP(Inventory Routing Problems)模型中加入了一致性要求，从而平衡了成本和服务质量要求。

通过对一致性车辆路径问题应用场景的梳理，可以发现一致性要求在实际中具有重要意义。一方面，对于被服务的客户而言，其享受到了更高质量的服务；另一方面，对于企业和服务人员而言，它有利于企业在激烈的市场竞争中获得优势，降低服务人员和司机的学习成本，提升人员的工作效率。

1.2 一致性需求的分类

ConVRP的一致性要求一般分为三类：时间一致性(Time Consistency, TC)、人员一致性(Driver Consistency, DC)和路线一致性(Route Consistency, RC)。TC表示在服务周期内，同一个客户在每个服务日的同一时间段内被服务，主要应用在快递配送、牛奶配送等场景中；DC表示在服务周期内，同一个客户每次都由同一个(或几个)服务人员服务，主要应用于家庭护理、家政服务等问题中；RC表示在服务周期内，企业给每个司机安排的路线尽量保持一致，主要通过考虑服务人员对路线或区域的熟悉程度来安排调度。TC和DC都是从客户角度出发进行研究，目的是提高客户满意度；而RC主要聚焦于企业，目的是提高管理效率，降低成本。

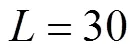
2 一致性车辆路径问题模型

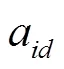
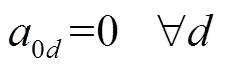
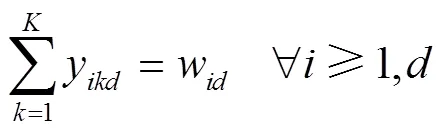
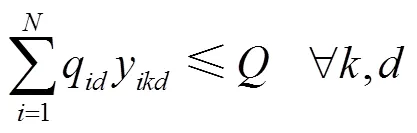
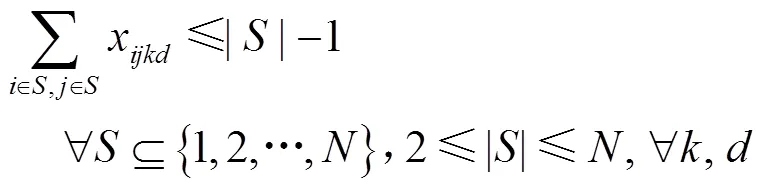
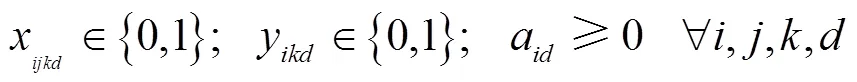
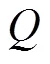
2.1 同时考虑TC和DC的ConVRP

Groër等[14]的模型具有开创性意义，后续的学者在研究ConVRP时都会参考该模型对问题进行建模分析。Tarantilis等[23]、Kovacs等[24]、Xu等[25]在后续对求解ConVRP算法的研究中也基本沿用了Groër的模型。Campelo等[26]以医药配送中心的实际案例为基础建立了具有TC和DC要求的ConVRP模型，基本思路与Groër的模型一致，区别是目标函数由原来的最小化总行驶时间改为了最小化总行驶距离，其根本目的都是最小化成本；Goeke等[27]将Groër的模型进一步优化，使得变量更少，从而利用精确式算法解决ConVRP；Stavropoulou等[28]考虑实际应用中的运输问题，在一致性车辆路径问题模型的基础上增加了对利润的考虑，在Groër模型的基础上将目标函数更改为最大化企业利润，对利润和一致的客户服务之间的权衡进行研究，得出了管理见解；Zhen等[29]考虑了逆向物流中的客户服务，将ConVRP与VRPSPD进行结合，定义了同时取送货的一致性车辆路径问题并建立了相应的混合整数规划模型，在处理TC与DC的做法上与Groër等[14]一致。

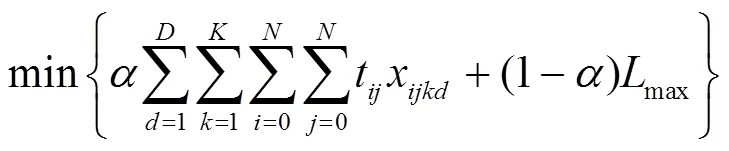
之后，Kovacs等[31]继续在单目标模型的基础上拓展，提出了多目标广义一致性车辆路径问题(Multi-Objective Generalized Consistent Vehicle Routing Problem，MOGenConVRP)，其将DC、TC以及最小化路径成本作为问题的多个独立目标。多目标优化方法能够在冲突的目标函数之间进行更彻底的权衡分析，从而使得研究结果能辅助物流公司在成本和服务水平之间进行权衡。Lian等[32]在研究中同样提出了一个多目标模型，将时间和人员一致性约束作为目标进行建模，该模型与Kovacs等[31]的模型类似，目标函数如下：

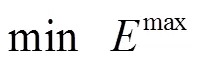
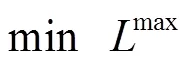
式中：目标函数(15)最小化总行驶时间；目标函数(16)寻求最大限度地减少拜访单个客户的不同司机数量，即最优化人员一致性；目标函数(17)使到达不同客户处的时间差最小化，即最优化时间一致性。

2.2 考虑TC或DC的ConVRP

以上模型都是同时考虑了TC和DC要求，也有少量问题只需要考虑这两种要求中的一种。Feillet等[33]针对残疾人交通问题设计了时间一致性的车辆路径问题模型，由于面对的实际问题不同，作者没有通过限制最晚和最早服务时间之间的差异来确保时间一致性，而是通过时间类进行时间一致性建模。作者定义了求解时间类最小类别数的模型，同时在Groër等[14]的模型基础上不考虑DC，将TC限制为每个客户允许的最大时间类别数，从而解决了残疾人交通的时间一致性车辆路径问题。

Lespay等[34]根据一个食品配送中心的实际问题，设计了有时间窗的人员一致性车辆路径问题。不同于Groër等[14]的模型中没有客户时间窗约束的假定，该问题基于标准的VRPTW对问题建模，将时间窗作为硬性约束，除此之外，该问题还考虑DC要求，即服务周期内每位客户只由一位司机来服务，但该问题不考虑TC要求。在传统的ConVRP中，驾驶员的数量是固定的，目标是最小化总行驶时间，同时，客户没有时间窗口限制，但是访问客户应该以最小的到达时间差来安排。而Lespay等[34]的模型以最小化驾驶员数量为目标，同时保证人员一致性要求。

2.3 考虑RC的ConVRP

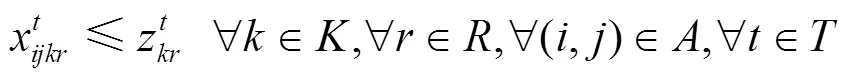
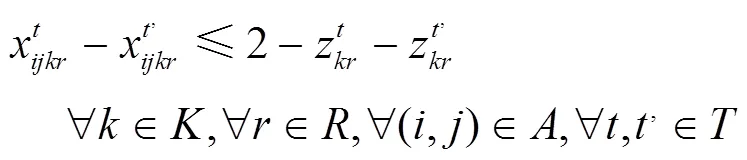
约束(18)和约束(19)保证了如果司机在不同的两天内行驶了同一条路径，则司机在这两天内访问的顾客及访问顺序是一致的。

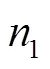
2.4 考虑其他条件的ConVRP

除了对TC、DC和RC要求的考虑，刘恒宇等[35]还研究了交通拥堵及快递人员工作量平衡性因素对配送路径的影响，通过在模型中增加拥堵因子、利用均方差的形式刻画工作量不平衡性，建立了混合整数规划模型并利用基于模板路径的模拟退火算法求解。结果发现：交通拥堵使最优配送路径的总行驶时间平均增加18.38%，使快递人员在任意两天到达同一顾客的最早与最晚时刻之差平均增加12.92%；当快递人员配件量的不平衡性平均下降35.82%后，二者仅分别平均增加2.29%和1.68%。黄琳[15]在论文中也考虑了路径一致性和工作量平衡的车辆路径问题，并分析了基于RC派生出的实际路径行驶方案带来的TC和DC效果。

综上，ConVRP建模方法汇总于表1。

表1 一致性车辆路径问题模型汇总

续表1

3 一致性车辆路径问题求解方法

VRP是NP-hard问题，由于参数与约束众多，求解较为困难，因此VRP求解通常使用启发式算法。ConVRP约束比VRP更为复杂，是一个NP-hard组合优化问题，因此大多数文献中采用的是启发式算法，极少数文献采用精确式算法。

3.1 启发式算法求解ConVRP

Groër等[14]首先提出了ConVRP并建立了整数规划模型，然而该模型仅适用于小规模问题，对于大规模问题并不适用，因此作者根据ConVRP问题的特点基于记录更新(Record-to- Record Travel, RTR)的算法设计了两阶段的启发式算法。在第一阶段，通过只考虑那些需要多天服务的客户来生成一组模板路线；在第二阶段，基于模板路线，通过从模板中删除在第天不需要服务的客户并加入仅在第天需要服务的客户来创建所有日期的路线。该过程既保证了客户在需要服务时总是由同一辆车来访问，又保证了客户访问的顺序将遵循优先原则。在设计路线的过程中主要采用局部搜索算法来改进路线，保证客户能在每天大致相同的时间接受服务。

Tarantilis等[23]设计了基于模板路线的禁忌搜索算法(Template-based Tabu Search Algorithm, TTS)，算法分为两阶段：首先，构建一个主模板路线时间表，以确定服务顺序和对需求频繁客户的服务分配；之后，基于主模板，为需求频繁和不频繁的客户设计多天的实际车辆路线和服务时间表。在模板路线的基础上，采用了禁忌搜索改进方法，以顺序的方式修改模板路线和实际的每日时间表，得到了比Groër等[14]的算法更好的结果：成本降低了4.76%，客户最大的等待时间差异降低17%，部署车辆的平均数量从10.5辆减少到9.9辆。Kovacs等[24]提出了一种基于模板的自适应大邻域搜索算法，在求解速度和质量上有了进一步提升。刘恒宇等[36]提出用基于模板路径的模拟退火算法求解ConVRP问题，算法分为两阶段，第一阶段求解模板路径，第二阶段以所得模板路径为参考获得各天车辆具体配送路径方案，两个阶段均采用模拟退火法进行优化，该方法在中小规模基准数据集上得到了良好的验证。卞晨[37]借助蚁群算法，通过两阶段的信息素更新规则求解ConVRP，并验证了算法具有较高的求解效率和求解质量。

对于GenConVRP，Kovacs等[30]没有采用基于模板路径的方法，而是基于灵活的大邻域搜索算法设计了几种破坏和修复试探法以便将顾客从路线上移除并重新插入到更合适的位置，TC约束通过简单的2-opt算子改善。对于MOGenConVRP, Kovacs等[31]通过多方向大邻域搜索算法最大可求解周期为5d、客户数量为199的大型算例，并且发现该方法在提升70%到达时间一致性的同时仅增长3.84%的行驶成本，优化效果较好。

Xu等[25]使用变邻域搜索算法解决ConVRP，该算法由两阶段组成。在第一阶段，应用变邻域搜索算法获得近似最优解，获得的解决方案可能不可行。如果解决方案质量可接受，则通过第二阶段使其可行并进一步优化。通过数值实验对比，该算法优化效果最好，尽管平均运行时间上相比Kovacs等[24]的算法要长，但是考虑现在的CPU计算性能，多出的运行时间可以忽略不计。Campelo等[26]在设计解决大规模算例的算法时，指出ConVRP的复杂性主要在于节点的数量，因此他们设计了一种基于FO(Fix-and-optimize)的方法，目的在于减少节点数量，试图利用其结构特点来解决这个问题；同时结合可变邻域分解搜索原理，通过将问题分解为只考虑解空间的不同部分来解决大规模的问题，作者利用该方法分析了一家医药分销公司的案例。Zhen等[29]分别根据记录更新算法、可变邻域局部搜索算法和基于禁忌搜索算法的原理提出了三种启发式方法，数值实验表明在小规模实例中，基于记录更新的启发式方法具有优势。但是，对于中等规模的实例，最好的选择是基于可变邻域局部搜索的启发式算法，它可以在10s内解决40个客户和5d的实例。吕文雅[38]开发了一个集成了记录更新算法、变邻域深度搜索算法和禁忌搜索算法的Web端系统，以便于使用相关算法对车辆路径进行优化。Lespay等[34]提出了一个两阶段启发式方法来最小化ConVRPTW的路线数量：第一步，基于插入启发法构造一个可行的初始解；第二步，通过启发式方法减少第一步中获得的解决方案中的路线数量；最后，根据总行驶距离重新优化第二步的结果从而获得最终解决方案。

3.2 精确式算法求解ConVRP

通过对以上文献中解决ConVRP问题的方法归纳可以发现，几乎所有的大规模ConVRP都需要利用启发式方法来求解，但是也有部分学者利用精确式算法求解该问题。

综上，求解ConVRP的算法汇总于表2。

表2 一致性车辆路径问题求解算法汇总

4 总结与展望

VRP作为物流与交通运输领域的经典问题，其求解方法已经逐渐趋于成熟，研究成果也较为丰富。但随着应用场景的不断丰富，新的需求及约束也不断被提出，VRP变种也层出不穷。在众多VRP变种中，ConVRP是相对较新的VRP变种，相关成果具有重要的实践和学术价值。本文从VRP分类、ConVRP背景介绍、ConVRP模型、ConVRP求解算法等方面对该问题进行了综述。

ConVRP的出现源于物流公司对客户服务水平的关注，在有固定需求的物流配送服务中，稳定一致的服务时间及服务人员有助于公司维护良好的客户关系，提升客户满意度，从而产生额外的经济效益。实践表明，对于物流公司而言，保持一致性的服务水平比节省1%～3%的成本更为重要。尤其是快递公司，其运营的核心在于为客户提供标准的、一致性的服务。同时，司机对于一致性的线路安排也更为熟悉，有利于公司提升运力管理效率，降低运营成本。除了在物流配送领域有用武之地外，ConVRP在家庭护理、供应商库存管理中亦有广泛的应用场景，具有重要的实践价值。

从ConVRP的模型来看，除了一致性约束外，模型的主要约束与经典VRP基本一致。现有的研究成果中，大多数ConVRP应用场景及模型同时考虑了TC和DC要求，在物流配送中尤其常见。少部分应用场景及模型仅考虑TC或DC要求，例如残疾人交通问题中仅需要考虑TC要求、家庭护理问题中则更侧重考虑DC要求。对于RC要求的研究相对较少，目前有两种处理方法：一种是根据司机对区域的熟悉程度设计路线，司机访问某区域线路的次数越多，单次访问成本就越低，通过最小化司机对配送区域的访问成本实现RC；另一种是通过计算不一致路段占总路段的比例量化路线一致性水平。此外，在目标函数的设计中，大多数文献采用单目标建模方法，目标多为考虑最小化总成本(行驶时间/行驶距离)或司机数量等；少部分文献采用多目标的建模方法，例如在考虑RC要求时增加最小化司机对配送区域访问成本的目标来实现RC，同时多目标模型能够在冲突的目标函数之间进行更彻底的权衡分析，有助于检验不同维度的一致性要求之间的关系。

从求解方法来看，绝大多数ConVRP都是通过启发式算法解决的，尤其是在时间周期达到或超过5 d、客户数量超过50的大规模算例中。常用的求解算法有基于模板路径的禁忌搜索算法、邻域搜索算法、模拟退火算法、蚁群算法等，其中Lespay等[34]利用多阶段启发式算法求解了时间周期为19～27 d、客户数量达1 600以上的超大规模算例。极少数的中小规模算例可以通过精确式算法求解，值得关注的是，Wang等[22]通过列切割与生成技术实现了利用精确式算法求解客户数达50的中型算例，进一步提升了精确式算法在求解ConVRP中的算例规模。

展望未来，对于有TC要求的ConVRP，可以考虑更多随机因素的影响，保证在不可预见的场景下访问客户时间的稳定性，例如考虑交通事故、交通管制、司机在客户处等待时间的不确定场景等；对于有DC要求的ConVRP，在考虑服务人员一致性的同时可以进一步考虑人员之间工作量的平衡；对于有RC要求的ConVRP，在量化RC水平的同时，可以进一步研究RC与TC和DC的关系，通过提升RC水平来优化TC和DC效果。在求解方法上，可以针对同时包含TC、DC和RC约束的ConVRP定制化设计启发式方法实现对大规模算例的求解，进一步丰富ConVRP的求解方法。

[1] DANTZIG G B, RAMSER J H. The truck dispatching problem[J]. Management Science, 1959, 6(1): 80-91.

[2] KONSTANTAKOPOULOS G D, GAYIALIS S P, KECHAGIAS E P. Vehicle routing problem and related algorithms for logistics distribution: a literature review and classification[J]. Operational Research, 2020: 1-30.

[3] CHOI E, TCHA D. A column generation approach to the heterogeneous fleet vehicle routing problem[J]. Computers & Operations Research, 2007, 34(7): 2080- 2095.

[4] LIN S, YU V F, CHOU S. A note on the truck and trailer routing problem[J]. Expert Systems with Applications, 2010, 37(1): 899-903.

[5] IORI M, SALAZAR-GONZALEZ J, VIGO D. An exact approach for the vehicle routing problem with two- dimensional loading constraints[J]. Transportation Science, 2007, 41(2): 253-264.

[6] GENDREAU M, IORI M, LAPORTE G, et al. A tabu Search algorithm for a routing and container loading problem[J]. Transportation Science, 2006, 40(3): 342-350.

[7] MONTANE F A T, GALVAO R D. A tabu search algorithmfor the vehicle routing problem with simultaneous pick-upand delivery service[J]. Computers & Operations Research, 2006, 33(3): 595-619.

[8] OLIVEIRA H B, VASCONCELOS G C. A hybrid search method for the vehicle routing problem with time windows[J]. Annals of Operations Research, 2010, 180(1): 125-144.

[9] FIGLIOZZI M A. An iterative route construction and improvement algorithm for the vehicle routing problem with soft time windows[J]. Transportation Research Part C: Emerging Technologies, 2010, 18(5): 668-679.

[10] GULCZYNSKI D, GOLDEN B, WASIL E. The period vehicle routing problem: new heuristics and real-world variants[J]. Transportation Research Part E: Logistics and Transportation Review, 2011, 47(5): 648-668.

[11] BELTRAMI E J, BODIN L D. Networks and vehicle routing for municipal waste collection[J]. Networks, 1974, 4(1): 65-94.

[12] 姜贵山, 姬长虹. 周期性车辆路径问题在物流中的应用: 案例研究[J]. 科学技术与工程, 2010, 10(11): 2694-2697.

[13] 庞燕, 罗华丽, 邢立宁, 等. 车辆路径优化问题及求解方法研究综述[J]. 控制理论与应用, 2019, 36(10): 1573-1584.

[14] GROËR C, GOLDEN B, WASIL E. The consistent vehicle routing problem[J]. Manufacturing & Service Operations Management, 2009, 11(4): 630-643.

[15] 黄琳. 考虑路径一致性和工作量平衡的车辆路径优化问题[D]. 上海: 上海大学, 2019.

[16] COELHO L C, CORDEAU J, LAPORTE G. Consistency in multi-vehicle inventory-routing[J]. Transportation Research Part C: Emerging Technologies, 2012, 24: 270-287.

[17] SMILOWITZ K, NOWAK M, JIANG T. Workforce management in periodic delivery operations[J]. Transportation Science, 2013, 47(2): 214-230.

[18] RICHARD T W. Vehicle routing for small package delivery and pickup services[M]// BRUCE G S R, EDWARD W. The vehicle routing problem: lastest advances and new challenges. New York: Springer, 2008: 475-485.

[19] HOLLAND C, LEVIS J, NUGGEHALLI R, et al. UPS optimizes delivery routes[J]. Interfaces(Providence), 2017, 47(1): 8-23.

[20] KOVACS A A, GOLDEN B L, HARTL R F, et al. Vehicle routing problems in which consistency considerations are important: A Survey[J]. Networks, 2014, 64(3): 192-213.

[21] BORSANI V, MATTA A, BESCHI G, et al. A home care scheduling model for human resources[C]// 2006 International Conference on Service Systems and Service Management. Troyes: IEEE 2006: 449-454.

[22] WANG K, LU Z, XIA J, et al. Routing optimization with generalized consistency requirements[Z]. Article Submitted to Transportation Science, 2021.

[23] TARANTILIS C D, STAVROPOULOU F, REPOUSSIS P P. A template-based tabu search algorithm for the consistent vehicle routing problem[J]. Expert Systems with Applications, 2012, 39(4): 4233-4239.

[24] KOVACS A A, PARRAGH S N, HARTL R F, et al. A template-based adaptive large neighborhood search for the consistent vehicle routing problem[J]. Networks, 2014, 63(1): 60-81.

[25] XU Z, CAI Y. Variable neighborhood search for consistent vehicle routing problem[J]. Expert Systems with Applications, 2018, 113: 66-76.

[26] CAMPELO P, NEVES-MOREIRA F, AMORIM P, et al. Consistent vehicle routing problem with service level agreements: a case study in the pharmaceutical distribution sector[J]. European Journal of Operational Research, 2019, 273(1): 131-145.

[27] GOEKE D, ROBERTI R, SCHNEIDER M. Exact and heuristic solution of the consistent vehicle-routing Problem[J]. Transportation Science, 2019, 53(4): 1023- 1042.

[28] STAVROPOULOU F, REPOUSSIS P P, TARANTILIS C D. The vehicle routing problem with profits and consistency constraints[J]. European Journal of Operational Research, 2019, 274(1): 340-356.

[29] ZHEN L, LV W, WANG K, et al. Consistent vehicle routing problem with simultaneous distribution and collection[J]. The Journal of the Operational Research Society, 2020, 71(5): 813-830.

[30] KOVACS A A, GOLDEN B L, HARTL R F, et al. The generalized consistent vehicle routing problem[J]. Transportation Science, 2015, 49(4): 796-816.

[31] KOVACS A A, PARRAGH S N, HARTL R F. The multi-objective generalized consistent vehicle routing problem[J]. European Journal of Operational Research, 2015, 247(2): 441-458.

[32] LIAN K, MILBURN A B, RARDIN R L. An improved multi-directional local search algorithm for the multi- objective consistent vehicle routing problem[J]. IIE Transactions, 2016, 48(10): 975-992.

[33] FEILLET D, GARAIX T, LEHUÉDÉ F, et al. A new consistent vehicle routing problem for the transportation of people with disabilities[J]. Networks, 2014, 63(3): 211-224.

[34] LESPAY H, SUCHAN K. A case study of consistent vehicle routing problem with time windows[J]. International Transactions in Operational Research, 2021, 28(3): 1135-1163.

[35] 刘恒宇, 汝宜红. 考虑交通拥堵及工作量平衡性的一致性车辆路径问题[J]. 西南交通大学学报, 2016, 51(5): 931-937.

[36] 刘恒宇, 汝宜红. 一致性车辆路径问题下基于模板路径的模拟退火法[J]. 交通运输系统工程与信息, 2015, 15(6): 177-183.

[37] 卞晨. 基于蚁群算法的一致性车辆路径问题的研究[D]. 淮南: 安徽理工大学, 2017.

[38] 吕文雅. 集配一体化一致性车辆路径问题研究[D]. 上海: 上海大学, 2020.

[39] COELHO L C, LAPORTE G. A branch-and-cut algorithm for the multi-product multi-vehicle inventory-routing problem[J]. International Journal of Production Research, 2013, 51(23-24): 7156-7169.

[40] SUBRAMANYAM A, GOUNARIS C E. A branch-and- cut framework for the consistent traveling salesman problem[J]. European Journal of Operational Research, 2016, 248(2): 384-395.

A Survey of the Consistent Vehicle Routing Problem

LI Lu-yao, SHEN Yi-fan, XIA Jun, SHEN Hai-hui

(Sino-US Global Logistics Institute, Shanghai Jiao Tong University, Shanghai 200030, China)

The vehicle routing problem (VRP) is a major research topic in the field of logistics and transportation. In recent years, to cope with the fierce market competition, increasingly more enterprises have begun to focus on how to reduce costs while ensuring service efficiency and service quality. Practice shows that improving the consistency of vehicle routing solutions can not only improve service efficiency but also significantly enhance customer satisfaction. Therefore, the VRP considering consistency constraints (also known as the consistent VRP (ConVRP)) has emerged. The ConVRP is a relatively new variant of the VRP, and the related research results have important practical and academic value. With the consideration of diverse consistency constraints and the development of related mathematical models and solution methods, a considerable amount of research has been accumulated on the ConVRP. This study summarizes the classification, background, models and algorithms of the ConVRP. Consistent constraints mainly include time consistency, driver consistency, and route consistency. Time consistency and driver consistency constraints are common, whereas route consistency constraints are more novel. ConVRP methods are usually based on heuristic algorithms, especially for large and medium-sized instances (with time periods of 5 days and >50 customers). For small and medium-sized instances (with time periods of 3～5 days and <50 customers), some exact algorithms also exhibit good performance.

logistics engineering;consistent vehicle routing problem; time consistency; driver consistency; route consistency; literature review

U116.2

A

10.19961/j.cnki.1672-4747.2021.07.036

1672-4747(2021)04-0062-13

2021-07-27

2021-08-08

2021-08-11

2021-07-27～07-30； 08-07～08-08

“科技助力经济2020”重点专项；国家自然科学基金项目(72031006)；上海交通大学科技创新专项(17JCYA04)

李路遥(1998—)，男，河北邢台人，硕士研究生，研究方向为物流优化，E-mail：liluyao20@sjtu.edu.cn

夏俊(1987—)，男，浙江杭州人，博士，助理研究员，研究方向为物流优化，E-mail：lgtxiaj@sjtu.edu.cn

李路遥，沈一帆，夏俊，等. 考虑一致性约束的车辆路径问题综述[J]. 交通运输工程与信息学报，2021, 19(4): 62-74.

LI Lu-yao, SHEN Yi-fan, XIA Jun, et al. A Survey of the Consistent Vehicle Routing Problem[J]. Journal of Transportation Engineering and Information, 2021, 19(4): 62-74.

(责任编辑：李愈)