注浆圈对高水位山岭隧道衬砌的结构影响分析

付 豪

（重庆市设计院，重庆市 400015）

0 引言

我国西南地区山岭众多，地势复杂，隧道工程作为最有效的交通方式得到了大量的应用，同时伴随而来的还有大量影响隧道安全运营的问题，其中高水位山岭隧道的突水灾害一直是隧道工程中研究的重点和难点问题[1-2]。富水山岭的高水压会对隧道结构造成一定破坏，甚至引发隧道局部渗漏和涌水灾害，影响人们的生命财产安全。

许多学者针对地下水位以下隧道注浆圈和衬砌共同作用的渗流应力场耦合问题开展了研究：李杰等[3]结合复变函数中的保角变换方法，推导了在注浆圈和衬砌共同作用下水下任意形隧道渗流场的解；应宏伟等[4]构造了“源-汇”系统，通过两个无限渗流场的叠加推导出水下大埋深隧道孔隙水压力以及隧道涌水量的解析解；路平[5]通过数值模拟方法，研究了地下水位、洞内限排等因素对渗流场、围岩与支护结构应力和位移分布的影响规律；贾善坡[6]建立了黏土岩弹塑性大变形渗流-应力耦合模型，并用ABAQUS 进行二次开发，得到了施工质量与围岩稳定性的关系。邹育麟等[7]采用FLAC 软件对富水隧道的3 种不同排水方式进行比较，并提出了合理的注浆圈加固参数、控制性排水量以及最优的防排水方式等。

综上所述，解决隧道工程中的渗漏问题需要对隧道工程中的渗流场和应力场进行综合分析。本文通过有限元分析软件MIDAS GTS NX 对某隧道工程渗漏问题进行渗流-应力耦合计算，并分析了在不同工况下衬砌的竖向位移、大主应力以及隧道涌水量的变化规律，为隧道渗漏提出科学治理方案。

1 计算理论

1.1 渗流-应力耦合理论

隧道往往处于一个复杂的地质环境中，这导致隧道会受到多重物理场的相互影响相互制约作用。对于隧道及地下工程，施工破坏了围岩原有的地下水平衡和应力状态，地下水渗流产生的孔隙水压力会以荷载的形式改变围岩的初始应力场。应力场的改变又会导致围岩结构属性的变化，使其渗透性能发生改变，此时渗流的分布又将随之变化。所以，对受地下水影响的隧道施工问题应考虑渗流-应力耦合分析。

MIDAS/GTS 中的渗流-应力-边坡模块可以实现隧道施工过程中的渗流-应力耦合分析，该模块首先进行渗流分析，然后运用计算所得到孔隙水压力推算出岩体中的地下水渗透力，进而将渗透力施加到模型上进行施工阶段的应力分析，经过交替迭代得到最终的耦合结果。渗流的基本微分方程如下：

式中：H 为总水头；kx为x 方向的渗透系数；ky为y 方向的渗透系数；kz为z 方向的渗透系数；Q 为流量；ω为体积含水率；t 为时间。

1.2 渗流-应力耦合计算基本方程

MIDAS/GTS 中使用的是加权残差的伽辽金法（G alcrkin），其基本方程为：

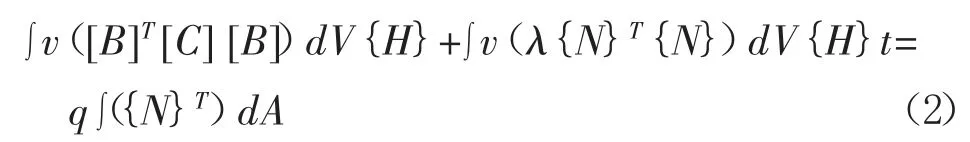
式中：[B]为动水坡度矩阵；[C]为单元渗透系数矩阵；{H}为节点水头向量；{N}为形函数向量；q 为单元边的单位重量；λ 为非稳定流的阻流项；{H}t 为随时间变化的水头。

2 模型及工况

2.1 有限元计算模型

在MIDAS/GTS 中建立高水位山岭隧道的有限元模型，见图1。为了消除边界效应对计算结果的影响，取模型宽度为隧道直径的10 倍，高度为隧道直径的8 倍，长度为50 m。整个模型为100 m×50 m×80 m 的箱体模型。围岩和注浆圈采用实体单元模拟，注浆圈厚度分别取3 m，6 m 和9 m，衬砌用析取的方式生成并采用板单元模拟，厚度为0.5 m。围岩、衬砌、注浆圈均为各向同性，隧道内水的渗流服从达西定律，衬砌内部为零水头。

图1 隧道模型网格划分图

为了更加准确地获得隧道衬砌处的变形、受力等数据的变化规律，所以衬砌及衬砌周围结构的网格划分更为密集，按1 m 进行网格播种，围岩部分则按4 m 播种，模型共计97 051 个单元。最后在模型的侧面施加X Y 两个方向的约束，底面施加X Y Z 三个方向的约束。荷载以节点水头的形式施加在模型的四周，隧道开挖断面设置为透水边界。模型各参数取值见表1。

表1 参数取值表

2.2 分析工况

采用控制变量法研究注浆圈渗透系数和厚度对衬砌结构变形的影响，建立注浆圈厚度分别为0 mm，3 mm，6 mm，9 mm 和渗透系数为2.5×10-8m/s，2.5×10-7m/s，2.5×10-6m/s，2.5×10-5m/s 的模型。具体模拟工况见表2。

表2 数值模拟工况表

3 注浆圈对衬砌结构的影响

3.1 隧道注浆圈厚度对衬砌结构竖向变形的影响

注浆圈厚度的选取主要考虑其止水程度和地层的承载能力，同时也需要考虑施工工期和成本的要求，本节主要研究注浆圈厚度对衬砌结构竖向位移的影响规律。模型中衬砌位移的观测点见图2。

图2 衬砌位移观测点示意图

注浆圈厚度不同时衬砌各观测点的竖向位移变化趋势见图3，从图3 中可以看出衬砌各位置处竖向位移绝对值的大小顺序为拱顶沉降值＞拱底隆起值＞拱腰沉降值>拱脚沉降值。注浆圈厚度从0 m增加到9 m 的过程中，拱顶处的竖向位移依次降低了54.9%、31.7% 和2.71%；拱腰处的竖向位移依次减少了68.3%，13.4% 和16.4%；拱脚处的竖向位移依次减少了36.5%，36.2% 和13.1%；拱底处的竖向位移依次减少了43.2%，24.5% 和16.6%，可以看出随着注浆圈厚度的不断增加，衬砌结构的竖向位移也在不断减少，但是减少的幅度逐渐降低，当注浆圈厚度超过6 m 之后，继续增加厚度对衬砌结构竖向位移的影响微乎其微，这说明增加注浆圈厚度可以在一定程度上控制衬砌的变形量，不过并不能一味地通过增加注浆圈厚度来控制衬砌变形，还需要考虑施工难度和经济成本。

图3 不同注浆圈厚度各观测点竖向位移变化图

3.2 隧道注浆圈渗透系数对衬砌结构竖向变形的影响

注浆圈渗透系数对其止水程度的影响也是不容忽视的，但是较低的渗透系数往往意味着更加优良的注浆材料和更高的成本，在工程中需要进行取舍。为了探究注浆圈渗透系数对衬砌竖向位移的影响，在控制注浆圈厚度为6 m 不变的情况下，改变模型中注浆圈材料的渗透系数，得到衬砌各观测点的竖向位移变化曲线见图4。

图4 不同注浆圈渗透系数各观测点竖向位移变化图

从图4 可以看出衬砌各位置处竖向位移绝对值的大小顺序为拱顶沉降值＞拱底隆起值＞拱腰沉降值＞拱脚沉降值。注浆圈渗透系数从2.5×10-5m/s减小到2.5×10-8m/s 的过程中，拱顶处的竖向位移依次降低了25.4%、36.3% 和11.9%；拱腰处的竖向位移依次减少了45.9%，41.1% 和23.2%；拱脚处的竖向位移依次减少了52.5%，45.6% 和14.5%；拱底处的竖向位移依次减少了40.4%，44.1% 和24.3%，说明衬砌结构的竖向变形会随着注浆圈渗透系数的降低而减少，不过减少幅度逐渐降低。

3.3 隧道注浆圈参数对隧道涌水量和衬砌大主应力的影响

注浆圈并不是通过分担衬砌外水压力来降低衬砌的应力，而是通过封堵地下水，减少注浆圈地下水渗入量来降低隧道的涌水量，以较小的排水量显著降低衬砌的外水压力，从而在一定程度上影响衬砌的应力分布。图5 是隧道涌水量和衬砌大主应力与注浆圈厚度的关系曲线，从图5 中可以看出注浆圈对隧道涌水量的影响较大，当注浆圈厚度从0 m 增大到3 m 时，隧道涌水量降低了77%，不过超过3 m之后隧道涌水量的降低幅度有所下降；衬砌大主应力随着注浆圈厚度的增加而减小，不过影响效果并不明显，衬砌大主应力只在10% 范围内波动。

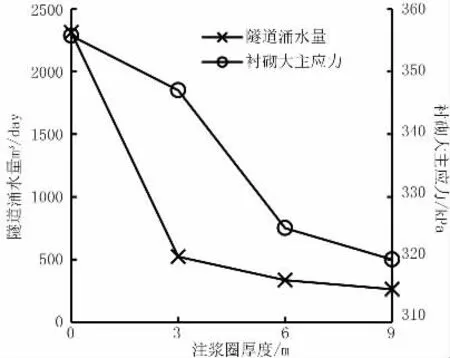
图5 不同注浆圈厚度下隧道涌水量和衬砌大主应力变化图

图6 是隧道涌水量和衬砌大主应力与注浆圈渗透系数的关系曲线，从图6 中可以看出随着注浆圈渗透系数的减小，隧道涌水量不断降低，当渗透系数降到2.5×10-8m/s 时隧道涌水量仅仅只有37 m3/d；衬砌大主应力随着注浆圈渗透系数的增加而减小，二者基本呈正相关关系，影响效果较为明显。综上所述，隧道涌水量造成的隧道应力，与隧道的排水设计量有关。较大的注浆圈渗透系数会导致大量地下水渗入，在隧道衬砌上产生高水压，隧道高水压可以直接表现为高压涌突水，也可能表现为隧道的局部塌方或大变形[8]。隧道按“以堵为主、防排结合”的限量排放原则，通过由注浆堵水圈、抗水压衬砌结构和防排水网络共同构成的防排水体系来达到限量排放的目的。

图6 不同注浆圈渗透系数下隧道涌水量和衬砌大主应力变化图

4 结论

（1）不同工况下衬砌各位置处竖向位移绝对值的大小顺序为拱顶沉降值＞拱底隆起值＞拱腰沉降值＞拱脚沉降值。

（2）随着注浆圈厚度的增加，衬砌结构的大主应力、竖向位移和隧道涌水量都在减小，不过竖向位移和隧道涌水量的减小幅度在注浆圈厚度大于3 m 之后都有明显的下降，而注浆圈厚度的变化只能引起衬砌大主应力的小幅度波动，且波动范围不大于10%。

（3）注浆圈渗透系数对衬砌结构的大主应力、竖向位移和隧道涌水量的影响效果较为明显，随着注浆圈渗透系数的降低，衬砌结构的大主应力、竖向位移和隧道涌水量都在减小，其中衬砌大主应力与注浆圈渗透系数大致呈正相关关系，衬砌竖向位移和隧道涌水量呈现出先急后缓的减小趋势。在实际工程中需要综合考虑安全、经济成本与施工难度等因素，合理地选择注浆圈渗透系数。