大跨度钢桁架人行天桥减震控制研究

王 军，杨 波，王泽银

（1.西安市政设计研究院有限公司，陕西 西安 710068；2.中国中铁一局集团有限公司，陕西 西安 710054）

0 引言

钢桁架结构由于其跨越能力较普通钢箱梁大，一般用于跨越较宽河流或者城市市政工程中。《城市人行天桥与人行地道技术规范》（CJJ 69—95）（简称《规范》）规定：“为避免共振，减少行人不安全感，天桥上部竖向自振频率不应小于3.0 Hz”。

大跨度人行天桥在满足相关规范要求的应力、强度和挠度等要求后，一般较难满足《规范》中的频率要求，因而往往给行人带来不舒适的体验。为改变此状态，工程上通常采用的办法有：（1）调整结构尺寸，增大结构刚度，但增大结构刚度的同时也会增大结构质量，故频率变化不明显且经济性较差；（2）设置减震设施，减少结构的振动响应，天桥常用的减震方式有安装调谐质量阻尼器（TMD），该方法具有造价低、安装方便、减震效果显著等优势[1]。

1 工程概况

广西河池园博园内拟设计1 座跨河钢桁架结构人行天桥（见图1）。桥梁采用3 跨简支结构，其中第2 跨为跨径80 m 的简支钢桁架梁。桁架高6.6 m，桁架结构均采用圆钢管，上弦杆截面尺寸为φ900 mm×30 mm，下弦杆截面尺寸为φ900 mm×26 mm，腹杆截面尺寸为φ450 m×（24～18）mm。桁架上面设置建筑装饰钢架，采用圆钢管，尺寸为φ450 mm×14 mm，桥梁横向共设置2 榀桁架。桁架横桥向间距7 m，桁架在下弦杆之间通过纵横梁焊接为一体，纵梁尺寸为300 mm×350 mm×16 mm，横梁尺寸为300 mm×400 mm×18 mm；桁架在上弦杆之间及装饰钢架在横桥向之间通过圆钢管焊接连接，钢管尺寸为φ450 mm×12 mm。

图1 钢桁架结构人行天桥

2 采用TMD 的消能减震设计

2.1 消能减震设计原理

调谐质量阻尼器又称动力吸振器，是结构被动控制措施的一种，主要应用于抗风和提高人体舒适性。调谐质量阻尼器系统由质量块、弹簧和阻尼元件组成[2]（见图2）。其原理是通过在主结构上增加一个辅助机构，在主结构受到外界动态力作用时，提供一个频率几乎相等，与结构运动方向相反的力，来抵消部分外界激励引起的结构响应。

图2 调谐质量阻尼器系统示意图

2.2 消能减震装置布置

本方案在结构上布置了5 个TMD，总质量为5 t，模型中TMD 采用集中质量模拟。减振装置设置在跨中下悬杆5 根横梁侧面，其平面布置图见图3，TMD设计参数见表1。

图3 TMD 减振装置平面布置图（单位：mm）

表1 TMD 设计参数

3 天桥的动力响应分析

3.1 建立有限元模型

针对该大跨钢桁架人行天桥，利用有限元分析软件Midas/Civil建立三维有限元模型，见图4；人行天桥有限元模型第2 阶模态竖向振动见图5；人行天桥有限元模型前3 阶振动频率见表2。

图4 人行桥三维有限元模型

图5 人行天桥有限元模型第2 阶模态（竖向振动）

表2 人行天桥有限元模型前3 阶振动频率

通过有限元计算分析可知，钢结构应力和变形都满足规范要求。结构竖向振动模态基频为2.079 Hz，不满足《规范》最小3.0 Hz 要求，需要对结构进行专项舒适度设计。另外，2.079 Hz 与行人正常行走步频2.0 Hz 非常接近，容易引起桥梁共振，因此对该大跨度人行天桥进行行人舒适度设计非常重要。

3.2 单人步行荷载

行人行走模型取国际桥梁和结构工程协会（IABSE）提供的连续步行荷载，行人不同运动形式下参数间的相互关系如表3 所示。由表3 可知，行人正常速度行走的频率为2.0 Hz，桥梁结构竖向振动模态基频应尽量避开此范围，防止引起结构共振。

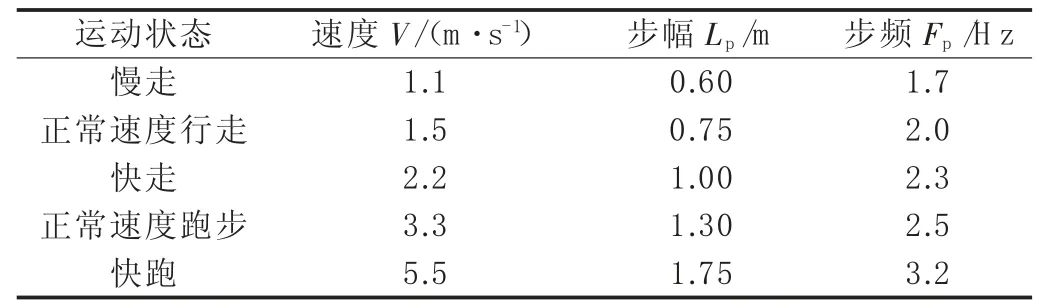
表3 行人不同运动形式下参数间的相互关系

3.3 人群荷载

实际工程中，一般都是将单人步行力按照一定的方式叠加，从而得到多人甚至人群步行力。由于行人间步行不一致，不同人的步行相互抵消，按照荷载等效原则，人数为N 的人群荷载可折减为Np（或Ns）个步调一致的行人产生的荷载，二者的比值称为同步概率。

针对不同密度人群的自由行走，《德国人行桥设计指南》（EN 03（2007））均采用谐波荷载模型，得到了低密度人群（密度＜1.0 人/m2）和高密度人群（密度＞1.0 人/m2）自由行走的等效计算公式。

低密度人群自由行走等效计算公式为：

高密度人群自由行走等效计算公式为：

式中：ζ 为振型阻尼；n 为人数。

3.4 人行荷载模拟

由于行人交通级别与人群密度相关，参考《德国人行桥设计指南》，给出了基于结构第1 阶竖向振动工况下的人群密度为0.7 人/m2（同阶频率为2.0 Hz）。竖向人群激励荷载曲线见图6。

图6 竖向人群激励荷载曲线

3.5 天桥减振动力分析

国内规范尚没有人行桥舒适度与振动加速度对应关系的表述，笔者参考《德国人行桥设计指南》，将两者之间的对应关系列出来，见表4。

表4 振动加速度限值 单位：m/s2

为了分析TMD 的减震效果，从有限元模型中提取加速度时程曲线（见图7、图8）和位移时程曲线（见图9、图10），对有无TMD 减震装置2 种工况进行对比分析。

图7 竖向无TMD 工况加速度时程曲线

图8 竖向加TMD 工况加速度时程曲线

图9 竖向无TMD 工况位移时程曲线

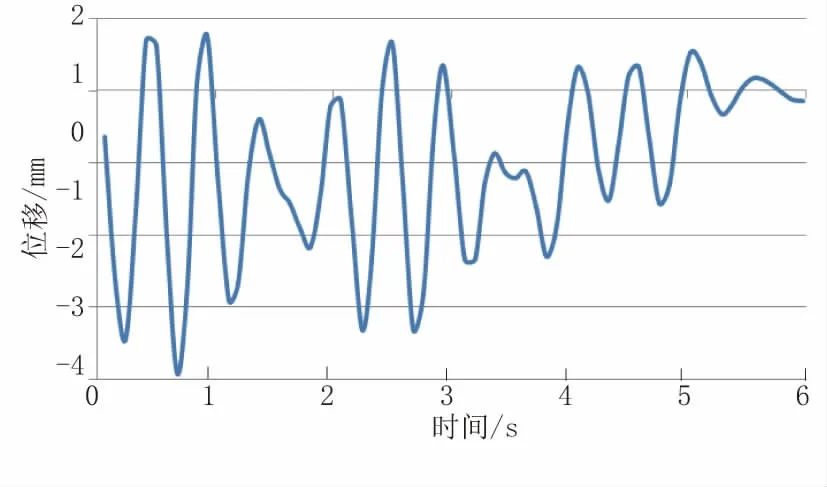
图10 竖向加TMD 工况位移时程曲线

由图7 可知，无TMD 时，竖向最不利点的稳态加速度为0.642 6 m/s2；由图8 可知，加上TMD 后，竖向最不利点的稳态加速度为0.490 6 m/s2，满足表4 舒适度等级1 的要求，同时竖向减振率为23.65% 。

由图9 可知，无TMD 时，竖向最不利点的位移为4.72 mm；由图10 可知，加上TMD 后，竖向最不利点的位移为3.94 mm，竖向减振率为16.5%。

4 结语

（1）采用TMD 减振技术后，能有效减小人行激励下结构的加速度，减震率达到23.65%，竖向位移减振率为16.5%，减震效果明显。

（2）国内规范中尚没有关于人行舒适度方面的评价指标，而国外相关标准和限制各不相同，建议加快人行桥TMD 减震系统相关规范的制定。