软土地区高桩承台结构斜桩应用数值模拟
2021-12-16鄢亚军
鄢亚军
(上海市水利工程设计研究院,上海市 200061)
0 引言
上海主要为软土地区,河道防汛墙结构通过设置桩基来控制挡墙位移和墙体不均匀沉降。若挡墙后方回填土高度较高,墙后地坪高程与河道底高程相差较大,会考虑采用叉桩或斜桩抵抗水平力,以满足水平位移控制要求。根据上海类似工程建设经验和《防汛墙工程设计标准》[1],防汛墙桩基水平位移和作用效应可以采用m 法计算。该方法假定土体为弹性变形介质,具有沿深度成正比增长的地基系数,用于对桩顶承受侧向外力的等截面单桩计算。该方法适用于直桩计算,应用于斜桩挡墙结构计算时,难以考虑多排斜桩桩土共同作用及对整体结构受力变形进行分析。根据桂劲松、汤子扬等[2-3]的研究得到,Plaxis 有限元软件在模拟板桩结构时,能较好地求解出墙后土体应力分布和结构变形。因此本文采用Plaxis 有限元计算软件对不同角度的叉桩桩基结构受力和变形特性进行模拟分析,研究叉桩结构在高桩承台结构中抵抗水平力和控制水平位移的规律,为选取合理的叉桩设计角度提供一定的依据。
1 工程设计方案
上海某住宅区河道设计河底高程为0.0 m,河道需满足游艇通航要求,河道一侧现状道路连接桥梁坡道,路面高程为6.50~7.50 m。由于现状路面为回填土压实,地下水位考虑为3.5 m,现场护岸布置空间受限,挡墙结构设计为高桩承台结构,拟比选采用三排φ800 灌注桩加前排(400×100×10.5)钢板桩及两排φ800PH C 管桩加前排(400×100×10.5)钢板桩的断面结构型式,如图1、图2 所示,该区域工程地质剖面如图3 所示。

图1 灌注桩直桩式高桩承台方案
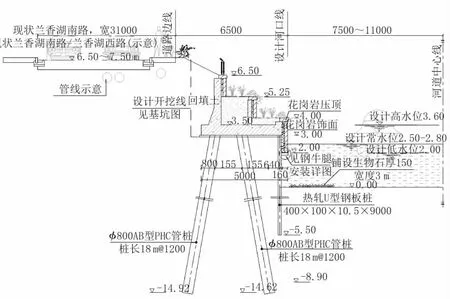
图2 叉桩式高桩承台方案

图3 工程地质剖面图
2 有限元计算模型建立
本研究采用Plaixs 3D 岩土软件建立高桩承台挡墙结构三维有限元模型。
2.1 土体本构模型选取
上海位于东海之滨,长江入海口处,属长江三角洲冲积平原。地质土主要由黏性土、粉性土及砂性土组成,大部分地区为正常固结和弱固结黏土及密实度较低的砂土。此类软土地基变形受体积应变影响较大。
目前常规用于数值模拟的土体本构模型主要为弹塑性的Mohr-Coulomb 模型、DrukerPrager 模型、DrukerPrager+Cap 模型、修正剑桥模型、非线弹性Duncan-Chang 模型、HS-Small模型等。上述土体本构模型的优缺点见表1。

表1 不同土体本构模型应用于软土地区的优缺点
比较上述六种土体本构模型可以看出,针对上海的弱固结土,HS-Small模型考虑了小应变范围内土体剪切刚度与应变的非线性关系。土体实测试验结果得到的土体剪切刚度—应变的关系如图4 所示,随着剪切应变增大,土体抗剪刚度G 呈“S”型衰减。由于防汛墙后土体的剪应变一般在0.01%~0.1% 之间[4-5],此范围内土体抗剪刚度是急剧衰减的,土体在小应变阶段的刚度要远大于较大应变阶段的刚度。本次土体参数见表2。

图4 土体剪应变-剪切刚度的关系

表2 本次土体模型参数
2.2 结构材料参数选取
Plaixs 中可以用板单元模拟具有一定抗弯刚度的二维薄壳结构,本文用来模拟挡土墙底板、墙身结构和钢板桩结构,灌注桩采用嵌入式梁单元(em bed beam)模块。本次模型各结构材料参数见表3。
2.3 计算模型
本次设计的住宅区河道横断为对称结构,故取一半建立模型进行有限元计算,模型尺寸为60 m×25 m(长×宽)。有限元计算模型网格划分如图5、图6 所示。
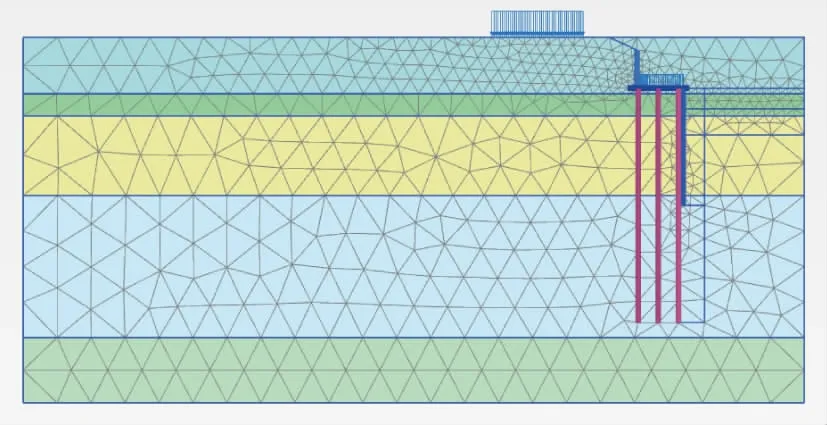
图5 直桩式高桩承台方案

图6 叉桩式高桩承台方案
2.4 工况选择
本次计算模型采用七种工况模拟:三排直桩式高桩承台结构及两排直桩式高桩承台结构,比较叉桩在12°、10°、8°、6°、4°五种设置角度下的桩顶位移及钢板桩承受的剪力与弯矩。
3 数值模拟结果对比分析
3.1 挡墙后侧土压力分布
通过Plaxis 有限元软件计算得到整体挡墙结构的∑Ux位移云图,如图7~图9 所示。由计算结果可知,挡墙桩基由三排直桩结构换成斜叉桩结构后,墙后土体的影响范围会增大,但土体位移的数值会减小。从直桩挡墙结构和斜叉桩挡墙结构墙后侧土压力分布图(图10)可以看出,直桩结构和叉桩结构墙后侧土压力分布基本一致,叉桩结构墙后土压力略有减小,主要是由于直桩高桩承台结构墙体位移大于叉桩结构墙体位移。

图7 三排直桩+钢板桩结构位移云图

图8 两排直桩+钢板桩结构位移云图

图9 两排斜12°叉桩+钢板桩结构位移云图

图10 两排直桩结构和斜8°叉桩结构墙后侧土压力分布图
3.2 挡墙底板位移
根据Plaxis 模型计算可知,当模型边界条件及土层地质条件一定时,在软土地区高桩承台结构中采用叉桩基础,可以有效减小挡墙桩顶位移,且叉桩倾斜角度越大,桩顶位移越小。叉桩倾斜角度在6°~8°之间时,桩顶位移减小得最明显(见图11)。
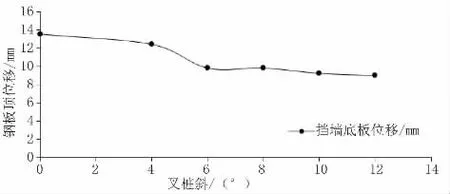
图11 钢板桩桩顶位移与叉桩角度设置关系图
根据模型计算得到的桩顶位移如表4 所示。

表4 挡墙底板位移值
3.3 挡墙前排钢板桩受力
根据Plaxis 模型计算可知,当模型边界条件及土层地质条件一定时,在软土地区高桩承台结构中采用前排钢板桩加后排叉桩的高桩承台结构;当叉桩角度一定时,可以有效减小钢板桩承受的最大弯矩和最大剪力,且一定范围内,叉桩倾斜角度越大,钢板桩承受的最大弯矩和最大剪力越小。根据模型的有限元计算,本次模拟的工况下,叉桩倾斜角度在6°时,钢板桩承受的最大弯矩和最大剪力最小(见表5、图12)。

图12 钢板桩承受弯矩及剪力与叉桩角度设置关系图

表5 挡墙前排钢板桩弯矩值及剪力值
4 结论与建议
(1)通过数值模拟发现,高桩承台结构应用斜桩基础后挡墙后侧土压力分布与直桩基础下基本一致,土压力数值略有减小。
(2)根据数值模拟计算结果可以看出,高桩承台结构应用斜桩基础后,可以有效减小挡墙底板位移,且底板位移大小随斜桩倾斜角度的增大而减小。当斜桩倾斜角度为6°时,挡墙底板位移减小得最明显。
(3)根据数值模拟计算结果可以看出,高桩承台结构应用斜桩基础后,当斜桩角度为0°~6°时,前排钢板桩承受的弯矩与剪力绝对值随倾斜角度增大而减小;当斜桩角度为6°~12°时,前排钢板桩承受的弯矩与剪力绝对值随倾斜角度增大而增大,斜桩倾斜角度为6°时,弯矩和剪力绝对值减小得最明显。
