对一道经典求极限问题的思考
2021-12-16李国强
四川文理学院学报 2021年5期
李国强
(贵州财经大学 数统学院,贵州 贵阳 550025)
0 引 言
极限是微积分的理论基础,[1]也是高等数学区别于初等数学的本质原因. 因此,极限问题是大学数学竞赛、考研数学等考试中必考内容之一.[2]计算极限的方法很多,包括直接代入法、两个重要极限、等价无穷小转换、洛必达法则、泰勒展开和拉格朗日中值定理等,很多时候需要这些方法同时交错进行. 笔者通过一道经典极限计算问题,一步步减弱题目中的条件,探讨新方法的适用性.
1 原始问题及其变形
要考虑的问题为
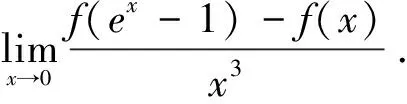
这里不急于解决该问题,我们先由强到弱改变题目中的条件.
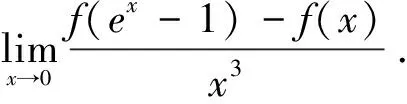
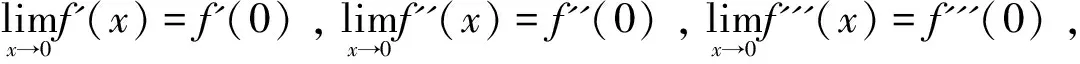
解:
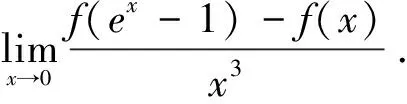
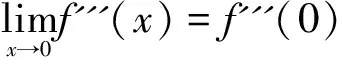
解:f(x)在x=0处展开:
所以,
由于x→0时,x~ex-1,所以o(x3)=o((ex-1)3),
从而
故
接下来有很多种方法可用,这里笔者采取对分子因式分解,然后利用等价无穷小量转化.

所以
注意,由于变形2中的条件比变形1中的弱,所以变形2中的方法仍然适用于变形1.
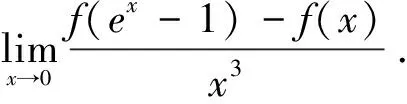
分析:该变形中的条件再次减弱,f(x)的三阶导数不一定存在,故不能采用泰勒展开的方法. 可先进行一次洛必达法则,观察会出现什么情况.

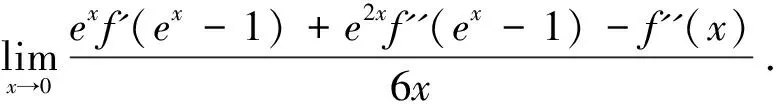
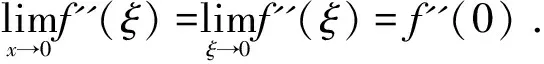
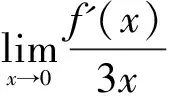
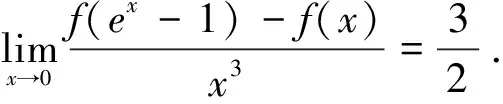
注意,变形3中的方法适用于变形1和变形3.
下面来看原始问题即变形4.
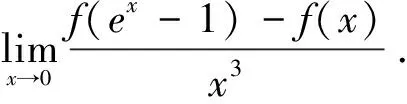
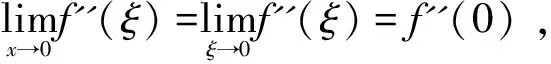
解:先用拉格朗日中值定理
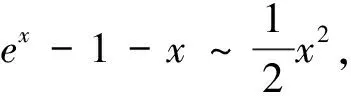
所以
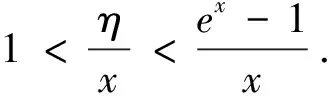
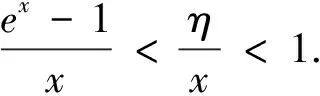
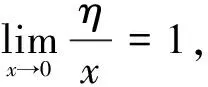
注意,变形4中方法适用于变形1、变形2和变形3.
结 论
原始题目的条件由强到弱经历了三次改变,每次改变所用的解法都适用于前面的变形. 针对不同的条件,灵活运用了几乎所有的求极限技巧. 比起一题多解,这种讨论问题的方式更加能够训练学生的发散性思维,[3]加深学生对数学严谨性、奥妙性的认识.
