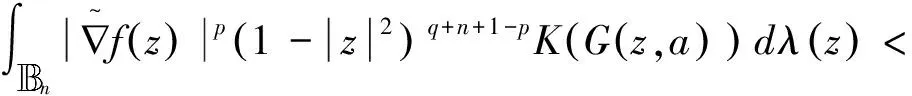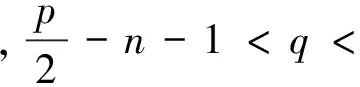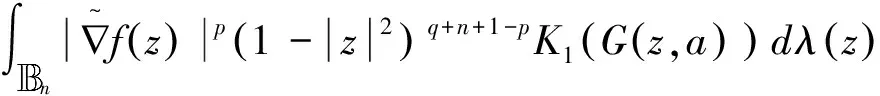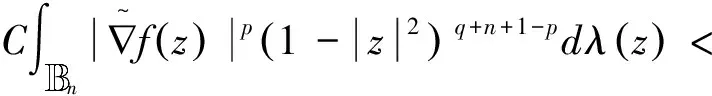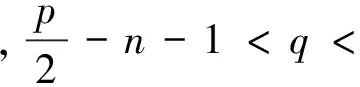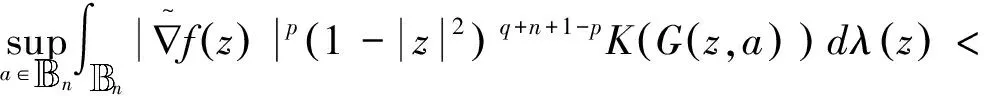单位球上QK(p,q)空间与F(p,q,s)空间的包含关系

胡 蓉

(四川文理学院 数学学院，四川 达州 635000)

1 预备知识

定义1[7]F(p,q,s)空间定义为：

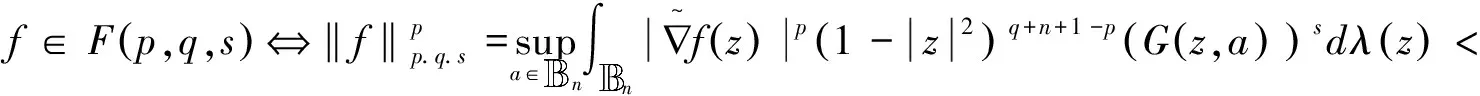
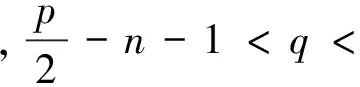
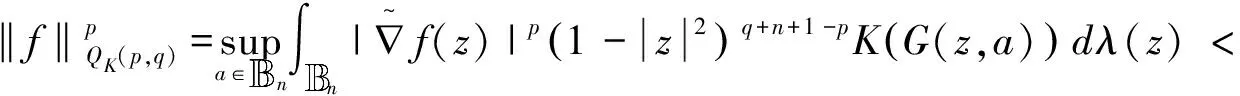
的全纯函数空间.

显然，当K(t)=ts时，QK(p,q)=F(p,q,s).

在下文中假设K(r)满足条件

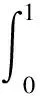
(1)

否则QK(p,q)为只包含常值函数的平凡空间.[3]

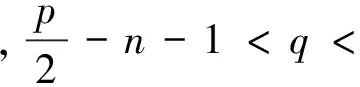
2 主要结果及证明

定理1 假设K(1)>0，记K1(r)=inf(K(r),K(1)),则QK(p,q)=QK1(p,q).

由f∈QK1(p,q)可得上式第二部分<∞，而第一部分有

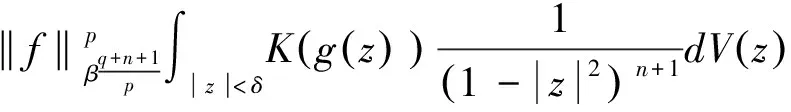
当0

故有

即f∈QK(p,q).得证.

证明：由定理1可知，QK(p,q)空间中核函数K可用一有界的权函数代替，因此不妨假设K1(r)0)，使得QK(p,q)=QK1(p,q).任取f∈F(p,q,0),

即有f∈QK1(p,q)，从而F(p,q,0)⊆QK(p,q).

证明：充分性.由定理2只需证K(0)>0时，QK(p,q)⊆F(p,q,0).由核函数K和G(z,a)的性质可得K(0)≤K(G(z,a))，从而任取f∈QK(p,q)，有

由K(0)>0，有f∈F(p,q,0)，即QK(p,q)⊆F(p,q,0)，得证.

必要性.如果K(0)=0，根据引理2，不妨设K(r)≤1,r∈(0,1)，记K1(r)=K(r)，K2(r)=K(1)，由K的单调性可得K1(r)≤K2(r)；又有

=∞

由引理2可得QK2(p,q)⊂QK1(p,q)，从而F(p,q,0)⊆QK2(p,q)⊂QK1(p,q)，与已知条件F(p,q,0)=QK(p,q)矛盾，所以K(0)>0.