均匀实验设计在化学反应动力学建模中的应用研究I.非线性代数动力学模型

胡葛林，吕 慧，曹贵平

联合化学反应工程研究所华东理工大学分所，华东理工大学化工学院，上海 200237

化学反应动力学是化学工程重要内容之一。根据反应动力学不仅可以解析反应过程机理、探究反应路径，还可以进行工业化反应器选型、设计、放大、优化、控制和预测。建立化学反应动力学模型的通常方法是：固定反应物初始浓度，测定不同反应温度、反应时间下反应物和产物的浓度，得到浓度和时间的关系数据；再利用非线性模型参数估计方法，迭代求解得到各温度水平下的速率常数和反应级数；进一步利用Arrhenius方程对温度进行拟合，得到频率因子和活化能。这种求取模型参数的方法需要开展大量的实验工作，存在工作量大、取样困难等问题。

Fang等[1-2]基于拟蒙特卡洛方法、数论方法和多变量统计分析提出了均匀实验设计思想，即在实验范围内选取一系列均匀分布的代表性点，以较少的实验次数解决多因素、多水平工艺优化和配方设计问题。

相较于全面实验、正交实验等传统实验设计方法，均匀实验设计的优势在于：（1）能够在实验域内选取一系列具有高度代表性且在空间内均匀分布的实验点，可近似替代全面实验设计；（2）不需要对模型有较深的认识，不对模型施加较强的假设；（3）可在合理的实验次数内为因素安排较多的实验水平，增强因素的感知度。因此，均匀实验设计在纺织、冶金、医药、化学化工和农业等领域得到了广泛应用[3-4]，其相关理论和应用还在不断发展中。Xin等[5]基于均匀实验设计进行沥青粘合剂配方优化，研究了硬质改性沥青性能和其组分配比之间的关系，以提升沥青高温性能。Li等[6]采用均匀实验设计系统研究了等离子体喷涂过程中电弧电流、Ar流率、H2流率、喷涂距离和粉末进料速率5个工艺参数对TiN涂层沉积效率、孔隙率、氧化物含量、显微硬度和断裂韧性的影响。此外，均匀设计能够在空间中生成均匀分布实验点的特点也引起了人们的极大兴趣[7]。在机器学习中，由于“更均匀”、“空间填充更多”的优势，均匀设计被用于模型选择，以提升支持向量机的一般性能，均匀设计的运用不仅大大减小了参数实验的次数，也提供了在计算时间限制下调整候选集大小的灵活性[8]。根据均匀实验设计的基本原理，也可将均匀实验设计用于高效求取反应动力学模型，可望大幅减少动力学实验的次数。基于此，本工作首次提出利用均匀实验设计原理进行反应动力学模型建立的实验设计，将反应温度和反应时间在其变化范围内均匀布置，每个温度下仅在一个时间点取样分析得到样品浓度，将参数对温度的依赖关系代入反应动力学模型，用非线性模型参数估计方法直接得到频率因子和反应活化能，对参数估计结果作统计学分析评估，较为系统地研究影响模型参数准度和精度的因素。

1 化学反应动力学模型

式中：Ci为物质i的浓度，mol/L；t为反应时间，min；k为反应速率常数，min-1。反应初始条件为：t=0时，CA0=1 mol/L，CB0=CC0=0 mol/L。根据Arrhenius方程，k与温度的关系为：

式中：k0为频率因子，min-1；E为活化能，kJ/mol；R为气体常数，J/(mol·K)；T为温度，K。将式（2）代入式（1），得到任意温度下动力学模型：

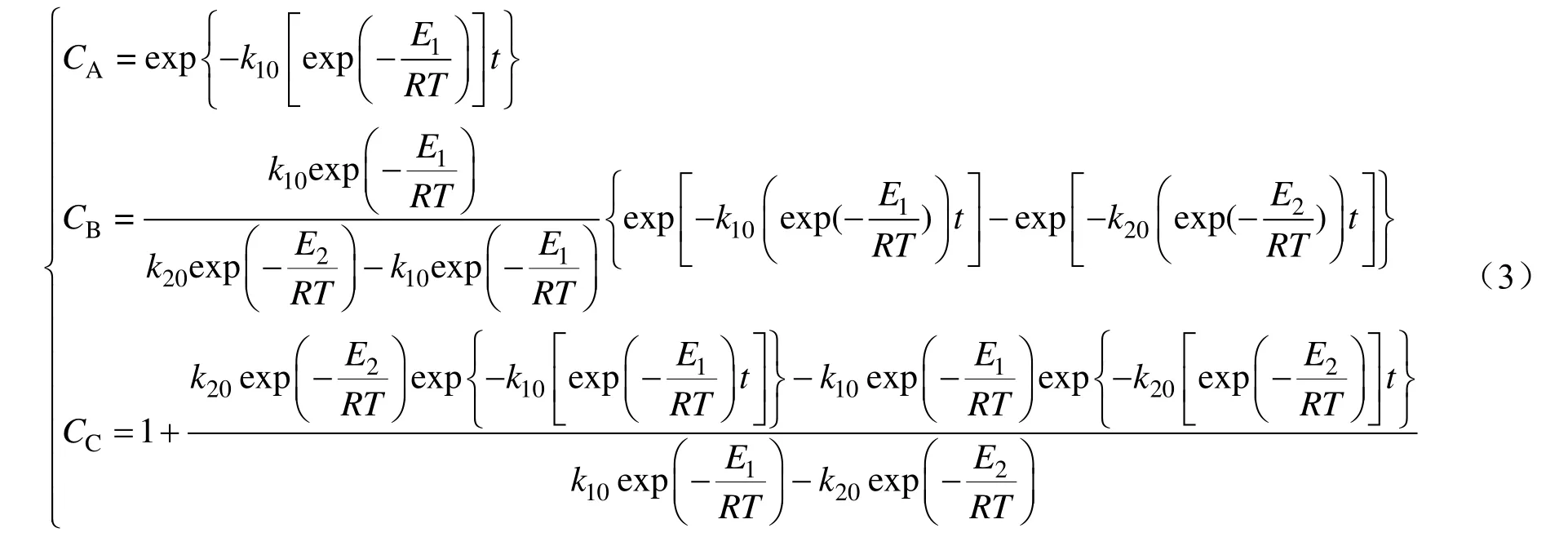
式（3）所示的动力学模型中待求参数有k10，E1，k20和E2。

控制反应物A的转化率在95%以内，基于前期探索，选择反应温度因素的区间为135～160 ℃，水平数为6个，步长为5 ℃；反应时间因素的区间为14～44 min，水平数为6个，步长为6 min，温度和时间的水平见表1。选用U6*(64)规划实验[10]，如表2所示，按表2中第1列和第3列安排实验。

表1 因素和水平Table 1 Factors and levels

表2 均匀表U6＊(64)Table 2 Uniform Table U6＊(64)

2 模拟实验数据的获取

采用随机数函数方法获得不同温度和不同时间下物质i的浓度实验值误差，进而得到实验值，如式（4）所示：

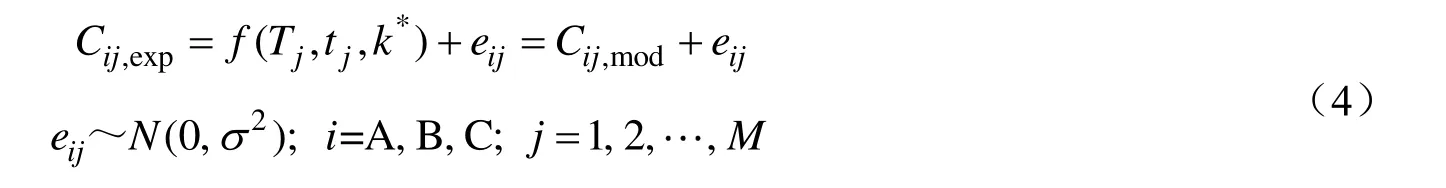
式中：Cij,exp表示第j组实验中物质i的浓度实验值，mol/L；Cij,mod表示第j组中物质i的浓度模型值，mol/L，通过式（3）计算得到；Tj表示第j组实验的反应温度，℃；tj表示第j组实验的反应时间，min；k*表示模型参数真值；eij表示第j组实验中物质i浓度的随机误差，eij服从数学期望为0、方差为2σ的正态分布；M表示实验组数，即均匀实验设计中温度和时间的水平数。

不同温度、时间下A，B和C浓度的模型值CA,mod，CB,mod和CC,mod是通过将模型参数的真值、温度和时间代入式（3）计算得到，为不失一般性，这里模型参数真值按照文献[9]方法计算给出：k10=6.856×1013min-1，E1=1.233 1×102kJ/mol，k20=1.500×1016min-1，E2=1.446 3×102kJ/mol。根据式（4）计算得到模型值Cij,mod，同时加上误差随机数eij得到模拟实验数据值CA,exp，CB,exp和CC,exp，随机误差eji由正态随机数函数计算产生。控制随机误差的标准差（σ）为0.001，得到的实验数据如表3所示，其中也列出关键反应物A的转化率（xA）。

表3 U6＊(64)实验设计及实验数据Table 3 U6＊(64) uniform design scheme and experimental data

由于各浓度的权值未知，参数估计时采用最大似然估计（MLE）目标函数[9]，如式（5），迭代算法为改进单纯形法（ISA）。

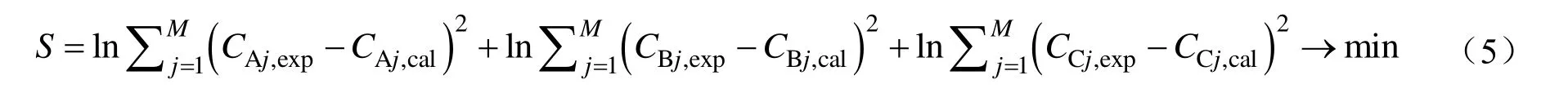
3 结果与讨论

3.1 模型显著性检验

利用式（5）目标函数，采用改进单纯形方法回归得到的模型参数估计值：k10=7.092 3×1013min-1，k20=1.565 2×1016min-1，E1=1.234 3×102kJ/mol，E2=1.447 8×102kJ/mol。相关系数R2=0.999 9，表明99.99%的观测值可以用此模型来解释[11]。将模型参数估计值代入反应动力学模型，在反应温度和时间范围内，浓度计算值以空间网格曲面表示，按均匀实验设计表U6*(64)安排的温度和时间下得到的CA,exp，CB,exp和CC,exp以圆点表示，如图1～图3所示。由图1～图3可知，实验点均匀地分布在实验范围内，与模型曲面有紧密的贴合，吻合很好，表明参数估计效果较好[12]。方差分析如表4所示。

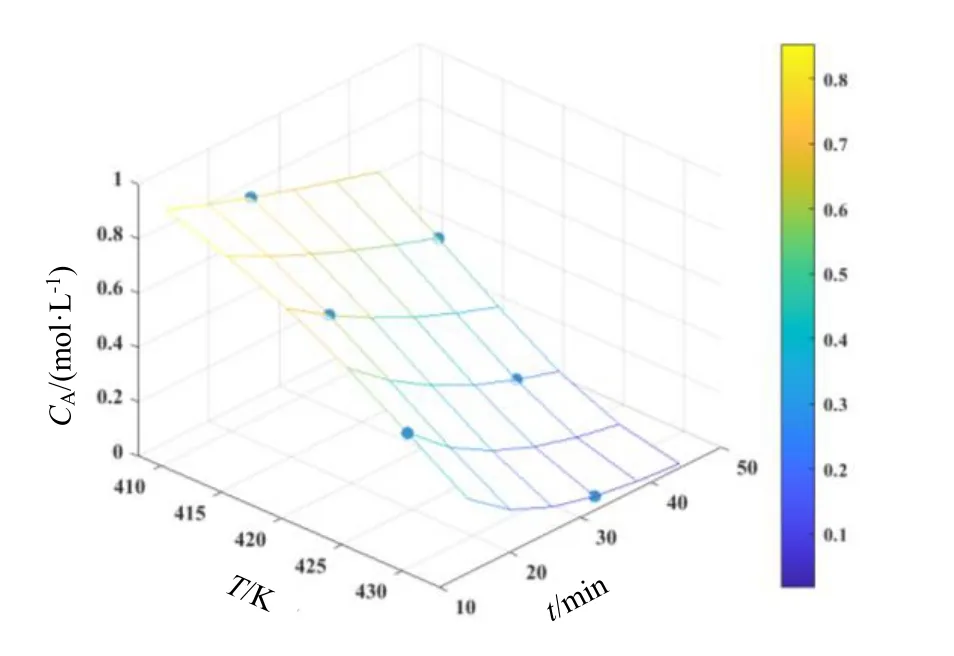
图1 CA随温度和时间的变化Fig.1 Surface plots of concentrations as a function of temperatures and time

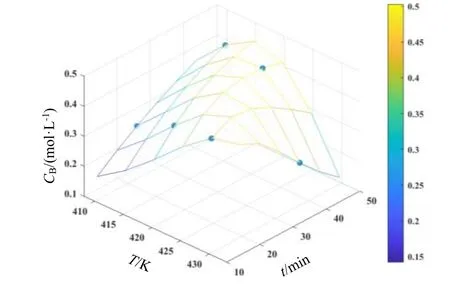
图2 CB随温度和时间的变化Fig.2 Surface plots of concentrations as a function of temperatures and time

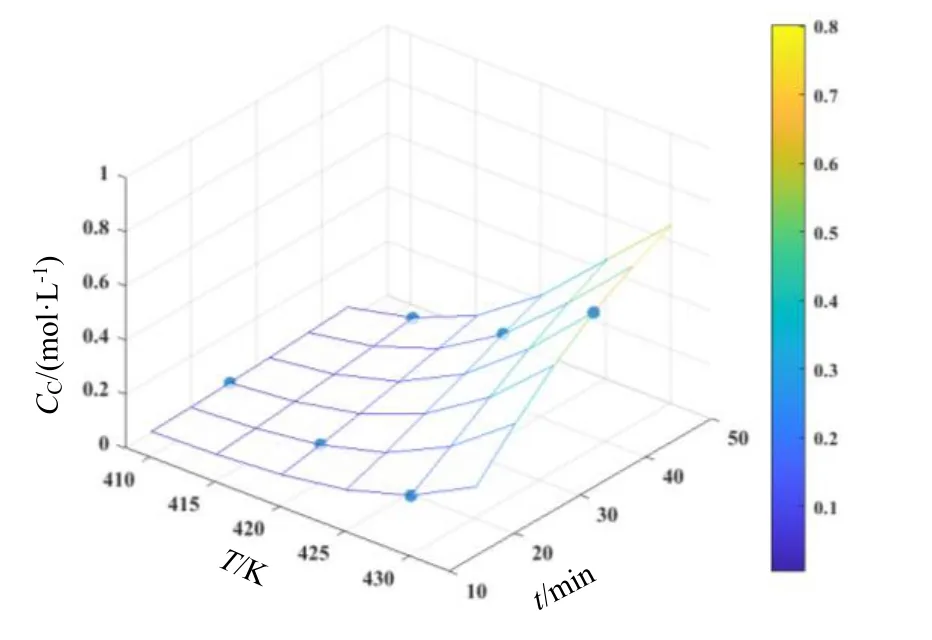
图3 CC随温度和时间的变化Fig.3 Surface plots of concentrations as a function of temperatures and time

表4 方差分析Table 4 Analysis of variance

表4中，DF表示自由度，F-value为回归均方和与残差均方和的比值，P-value为假设概率。对于非线性模型，当F-value大于10倍Fα，可以认为模型在α置信水平下是显著的[13]。由表4可知，反应动力学模型的F-value=7.14×105F0.01(4,14)=50.4，表明所得到的动力学模型具有99%的置信度。P-value=5.45×10-370.01，表明模型在统计学上是高度显著的[14]。

为了验证和方便比较模型参数估计效果，计算了参数估计值与真实值的相对误差（ε），结果如表5所示。由表5可知，各模型参数估计值与真值的相对误差均在5%以内。可以看出，利用均匀实验设计将温度和时间因素在变化范围内均匀分布，每个温度下仅在一个时间点取样分析，仅安排6次实验就能获得反应动力学模型参数。通常，为了建立动力学模型，对于温度和时间两个因素的实验，温度需要安排至少5水平，时间需要安排至少10水平，至少需要50次实验，实验周期很长，特别是在高温、高压等苛刻条件下在线取样困难，而且多次在线取样会造成间隙反应器中的物料损失，影响后续反应动力学行为，带来不可低估的实验误差，影响动力学模型的准确性。而通过均匀实验设计，实验次数减少到6次，实验工作量大幅减小，用少量的实验即可获得实验数据，因实验数据空间的均匀性，具有动力学规律的空间代表性，因而得到的模型参数值具有很好的准确性和精确性，表明均匀实验设计在多因素、多水平动力学模型建立中有着显著优势[15]。

表5 参数估计值及其与真实值的相对误差Table 5 Parameter estimation values and relative errors between estimated values and real values

3.2 实验随机误差的影响

在3.1节中，控制A，B和C浓度的实验值与模型值之间的随机误差标准差（σ）为0.001，但在实际问题中的随机误差可能会更大。保持温度、时间变化范围和水平、参数初值不变，探究了实验随机误差对参数估计精度的影响，结果见表6。由表6可知，实验误差标准差为0.001～0.1时，对参数估计结果不会产生影响；若进一步增大σ至0.25或0.5，出现浓度计算值为负数或大于初始值的异常结果。可见σ≤0.1可以得到满意的结果。

表6 不同实验随机误差标准差下的参数估计值和真值的相对误差Table 6 The relative errors between estimated values and real values under different σ

3.3 因素水平的影响

由于均匀实验设计所需的实验组数等于因素的水平数，可以改变因素在变化范围内的水平数来增大或减少实验次数，以满足不同实验条件要求和参数估计准度和精度的需要[16]。表7汇总了不同水平数对参数估计值的影响。由表7可知，在各个水平数下，4个模型参数估计值和真值的相对误差均可控制在6%以内，E1和E2的参数估计精度明显优于k10和k20，E1和E2的参数估计值与真值的相对误差保持在1%以内。总体来说，不同因数水平下的参数估计结果均令人满意。

表7 不同因素水平下的参数估计值和真值的相对误差Table 7 The relative errors between estimated values and real values under different levels

3.4 拟水平的影响

采用拟水平的方法，仍保持温度的变化为135～160 ℃，将温度的水平数减小到3个，分别为135.0，147.5和160.0 ℃；时间的变化范围和水平数不变，即14～44 min，水平数为6个。将表2均匀表U6*(64)中第1列的水平数进行合并：[1,2]→[1]，[3,4]→[2]，[5,6]→[3]，得到拟水平的均匀实验设计表U6(3×6)，如表8所示。参数估计结果和估计值与真实值的相对误差如表9所示。

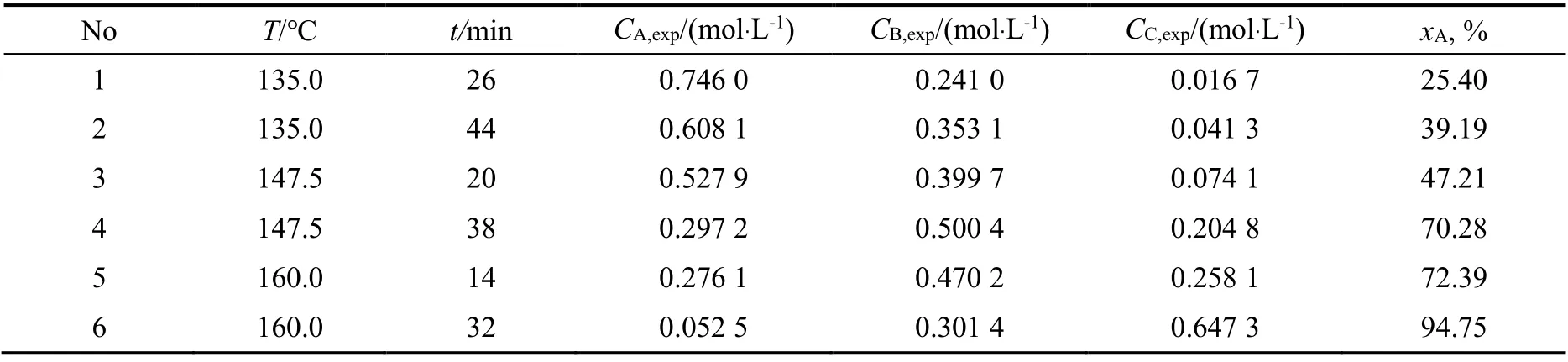
表8 U6(3×6)实验设计及实验数据Table 8 U6(3×6) uniform design and experimental data

表9 拟水平下参数值及其与真实值的相对误差Table 9 Estimated values of parameters and relative errors between estimated values and real values under pseudo level

拟水平实验设计参数估计结果与均匀实验设计参数估计的比较结果见表10。由表10可知，拟水平实验设计参数估计结果与非拟水平的均匀实验设计无显著差异，最大参数估计值与真值的相对误差为k10时的3.47%，拟水平实验设计的应用在保证参数估计精度的同时，将温度水平数从6个减小到了3个，提高了实验效率。

表10 拟水平均匀实验设计与均匀实验设计的参数估计结果比较Table 10 Comparison about parameter estimation results between Pseudo-level and uniform level

4 结 论

根据均匀实验设计原理和方法，首次提出在温度和时间二维空间内均匀布局实验点，获得建立化学反应动力学模型的“浓度-温度-时间”数据，仅用6组实验数据，便可一步完成模型参数的估计，为高效建立动力学模型提供一种新思路和新方法。参数估计值与真值的相对误差可控制在5%以内，统计分析表明模型参数估计结果具有良好的准确性、可靠性和显著性。不同实验误差方差下得到的参数估计结果基本一致，可控的实验误差对参数估计结果的影响可以忽略。不同水平数下，模型参数估值和真值的相对误差均可控制在6%以内，参数估计结果并不会因因素水平数的改变而发生明显变化，可以用最少的实验获得动力学模型参数。拟水平均匀实验设计的运用可以将温度因素的水平数进一步减小到3个，同时保证参数估计值有较高的精度。