薄膜型声学超材料隔声特性研究
2021-12-15王翌伟徐晓美LeeHeowPueh
王翌伟,徐晓美,林 萍,Lee Heow Pueh
(1.南京林业大学 汽车与交通工程学院,南京 210037;2.新加坡国立大学 机械工程系,新加坡 117576)
受质量作用定律限制,传统隔声材料的低频隔声性能较差,若一昧追求低频隔声性能,则要求材料厚度大大增加,这与轻量化设计要求相违背。声学超材料具有负质量密度及负体积模量特性,可以打破质量作用定律,使其能够在满足轻量化设计的同时具有较好的低频隔声性能[1]。目前,声学超材料包含局部共振膜型、周期性共振器/散射或声子晶体类型。这些超材料显示出不同寻常的声学特性,例如负有效质量[2]、负模量[3]、带隙[4]、可调带隙[5]等。其中,薄膜型声学超材料(Membrane-type Acoustic Metamaterial,MAM)在膜厚度较低的情况下,仍具有较好的低频隔声性能,因此,近些年来受到了较多的关注[2,5-8]。
MAM 是香港科技大学杨志宇等[2]基于共振理论提出的,它为轻量化低频隔声提供了新途径。薄膜型声学超材料由附加质量的弹性张紧薄膜固定在支撑框架上而构成,研究发现此结构不仅具有良好的低频隔声性能而且厚度低至mm级。Lu等[9]将有限元仿真与实验相结合,探索了膜上偏心质量的分布对于MAM 声学性能的影响,并通过对分布形式进行优化而获取较好的低频声学性能。刘忠远等[10]建立了通孔类MAM 的理论计算模型,研究了薄膜面密度与张力对隔声带宽的影响,并通过有限元仿真验证了理论模型的可靠性。叶超等[11]通过有限元法分析了MAM 微结构特征参数对一定频段内MAM 的传声损失的影响。Li 等[12]创造性地将聚乙烯醇/石墨烯(PVA/GR)纳米复合膜引入到MAM中,尝试通过施加外部电场来调节膜的有效模量,从而实现MAM声学性能的调节。
本文基于上述研究背景,对一种摆臂质量块式声学超材料展开较为系统的研究,以掌握这种MAM单胞的隔声性能及其影响因素,为此类声学超材料的设计提供理论指导。同时,探讨将MAM 单胞的组合应用在汽车前围板上以提高前围板低频隔声性能的可能性。
1 MAM隔声机理
MAM 可以看成一个“弹簧-质量”系统,薄膜相当于“弹簧”,附加在薄膜上的质量块相当于“质量”,刚性框架主要用于固定施加了预紧力的薄膜。当“弹簧-质量”系统受弹性波作用时,系统将在谐振力作用下做简谐振动。薄膜的振动方程可表示为[13]:

式中:c=,T为单位长度上薄膜受到的张力,σ为薄膜的面密度,η为薄膜上一点离开平衡位置的垂直方向位移。
MAM属于分布参数系统,其振动位移与薄膜上的径向位置有关,不同径向位置处的振动位移是不同的,因此对圆形薄膜通常采用等效集中参数来表征其振动特性。薄膜的振动可以等效为圆心处有一个等效集中质量为Men的质量块在等效弹性系数为Ken的等效弹簧作用下的振动。从能量等效角度分析,可以得到圆形薄膜的等效质量为[13]:

式中:m为薄膜的实际质量,可表示为πα2σ,α为薄膜的周界半径,J1(μn)为1阶柱贝塞尔函数。
若在薄膜圆心处增加一质量块M,可得单个元胞薄膜型超材料的振动固有频率为:

由式(3)可知,改变薄膜和质量块的相关参数可以改变声学超材料的振动固有频率。当入射声波频率与薄膜型声学超材料的固有频率接近或一致时,薄膜系统将发生共振,此时的声透射量最大,隔声效果最差;当质量块附近的薄膜振动位移与其余四周处的薄膜振动位移反相时,整个薄膜的平均振动位移约等于零,此时引起的声透射量几乎为零,声学超材料将获得最大的隔声量,此时的频率即为薄膜质量块系统的反共振频率,也即为薄膜型声学超材料隔声时的工作频率。
2 MAM隔声性能仿真模型构建
图1 为周国建等设计的摆臂式MAM 单胞结构[14],该子单胞内被引入多态反共振模式,可以拓宽MAM的低频隔声频带,并提高其隔声量。图中框架和摆臂均采用乙烯-醋酸乙烯共聚物(EVA)板材,薄膜为聚酰亚胺薄膜,质量块为金属薄片,摆臂长40 mm,宽4 mm,框架宽5 mm,其它相关结构参数和材料参数如表1所示[14]。

表1 MAM相关结构与材料参数[14]
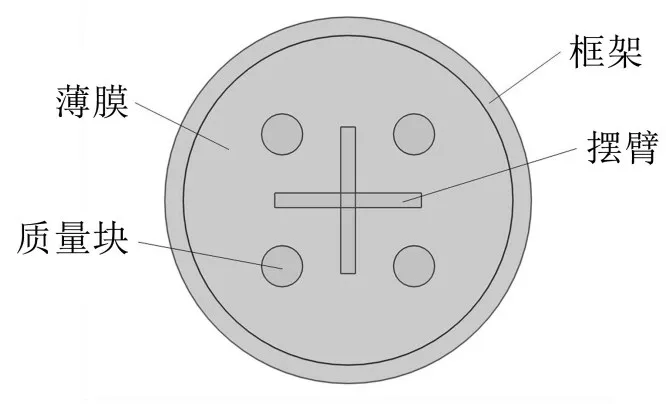
图1 MAM单胞结构示意图[14]
为进一步探讨图1 中MAM 单胞的相关设计参数对其隔声性能的影响,本节首先基于COMSOL软件建立了MAM 单胞隔声性能分析的仿真模型,如图2所示,其主要由空气域和MAM单胞组成。
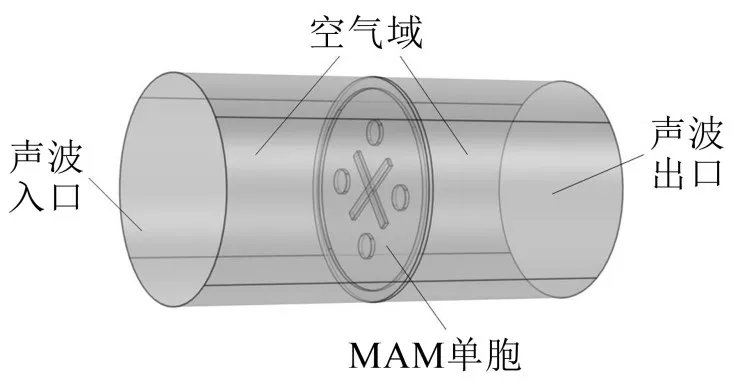
图2 MAM单胞隔声性能仿真模型
MAM单胞被安放在空气腔中央,平面波从声波入口处入射,遇到MAM单胞后,一部分声波被反射回去,一部分声波能量局限在MAM单胞内,还有一部分声波穿过MAM单胞继续传播。由于本文主要考察不同频率下MAM 的隔声性能,不考虑声波强度的影响,因此设置入射声波声压为1 Pa。设定MAM 单胞框架、薄膜四周为固定边界,声波出口处为无反射边界。为保证仿真分析过程中无外界声波透入,将空气域四周边界设为硬声场边界。设定空气密度为1.29 kg/m3,声波在空气中传播速度为340 m/s。
按照表1完成MAM单胞结构的相关参数设置,然后对仿真模型进行网格划分。因为薄膜厚度较小,为了尽可能地保证计算精度,同时又兼顾计算时间,选择用户控制网格划分,对最大和最小网格进行定义。模型网格划分的结果为:128 867 个域单元、22 180 个边界元、1 317 个边单元和329 107 个总自由度。
隔声性能通常用传声损失来表征,传声损失是指声波入射到隔层时,入射声强度级与透射声强度级之差。传声损失越大,隔声性能越好。取隔声性能分析的频率范围为10 Hz~1 000 Hz,求解步长为10 Hz,利用声固耦合模拟方法,在平面波入射边界和无反射边界分别对声波功率进行面积积分,并代入传声损失计算式,即可得到平面波通过MAM 单胞结构的传声损失。
3 隔声性能单一影响因素分析
本节基于所建立的MAM单胞的隔声性能分析仿真模型,研究薄膜厚度、质量块厚度、薄膜预应力以及摆臂厚度对其隔声性能的影响。
3.1 薄膜厚度对隔声性能的影响
在MAM中膜相当于振动系统中的弹簧。由前面的理论分析可知,薄膜厚度增加将引起MAM 振动系统的等效质量和等效弹性系数都发生变化。为考察薄膜厚度变化对MAM 单胞隔声性能的影响,取薄膜厚度分别为0.2 mm、0.3 mm 和0.4 mm,其他参数不变,基于所建立的隔声性能分析仿真模型计算MAM单胞的传声损失,计算结果如图3所示。
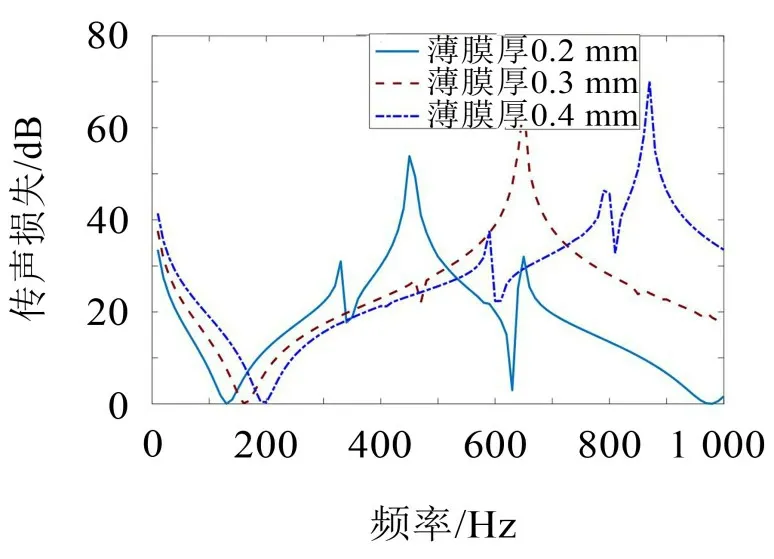
图3 薄膜厚度对传声损失的影响
由图3可以看出,随着薄膜厚度的增加,整个传声损失曲线整体向高频移动,传声损失第一谷值所对应的频率增大,传声损失峰值及其所对应的频率均明显增大,高传声损失的频带变宽。
3.2 质量块厚度对隔声性能的影响
改变质量块厚度实际就是改变质量块的质量,由前面的理论分析可知,质量块质量增加将引起MAM振动系统的等效质量变化,从而引起等效集中参数系统振动固有频率的变化。为考察质量块厚度变化对MAM单胞隔声性能的影响,在表1中其他参数不变的情况下,取质量块厚度分别为1.8 mm、2.4 mm、3.0 mm,基于所建立的隔声性能仿真分析模型,计算MAM单胞的传声损失,计算结果如图4所示。
由图4 可见,质量块厚度的改变并不影响传声损失曲线的总体变化趋势,但随着质量块厚度的增加,传声损失曲线整体向低频区域移动,尤其在300 Hz~500 Hz 范围内。传声损失第二峰值所对应的频率明显随质量块厚度增加而减小,传声损失峰值也有所下降。由此可见,通过调整质量块的厚度可以在某些频率范围内调节传声损失峰值及其所对应的频率。
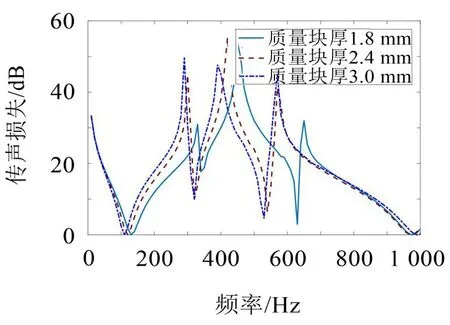
图4 质量块厚度对传声损失的影响
3.3 摆臂厚度对隔声性能的影响
为考察摆臂厚度变化对MAM单胞隔声性能的影响,在表1中其他参数不变的情况下,取摆臂厚度分别为1.6 mm、2.0 mm、2.4 mm,基于所建立的隔声性能仿真分析模型,计算MAM单胞的传声损失,计算结果如图5所示。

图5 摆臂厚度对传声损失的影响
由图5可知,改变摆臂厚度并不影响MAM单胞传声损失曲线的总体变化趋势。传声损失波谷值及其所对应的频率几乎与摆臂厚度的变化无关,最大传声损失及其所对应的频率,即MAM 单胞的工作频率,受摆臂厚度变化的影响均很小。这主要是因为MAM单胞的振动常发生在框架与十字摆臂组成的子单胞内,十字摆臂此时相当于子单胞的框架,仅起到支撑的作用,仅在一些特殊频率下,十字摆臂才会发生振动,从而影响MAM 单胞的传声损失。所以,MAM单胞的传声损失总体来说受摆臂厚度变化的影响很小。
3.4 薄膜预应力对隔声性能的影响
改变薄膜预应力即是改变薄膜平面上张力大小,改变薄膜平面上张力大小即是改变薄膜的等效刚度,从而影响薄膜型声学超材料的整体刚性。为考察薄膜预应力变化对MAM 单胞隔声性能的影响,在表1中其他参数不变的情况下,取薄膜预应力分别为1 MPa、2 MPa、3 MPa,基于所建立的隔声性能仿真分析模型,计算MAM单胞的传声损失,计算结果如图6所示。
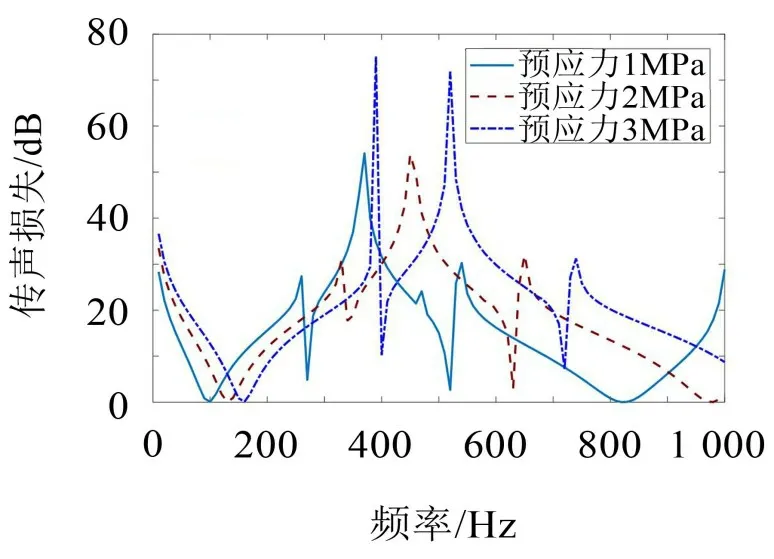
图6 薄膜预应力对传声损失的影响
由图6 可知,随着薄膜预应力的增加,MAM 单胞的传声损失曲线整体向高频区域移动,传声损失峰值明显增大,峰值和谷值所对应的频率均变大,MAM单胞的有效隔声频率范围变宽。
4 隔声性能多因素影响分析
由上述单一因素影响分析可知,对于MAM 单胞,对隔声性能影响较大的参数分别是薄膜厚度、质量块厚度和薄膜预应力。现将这3个参数选为正交试验设计的优化因素,各因素的取值见表2 所示的因素水平表。
正交表是一套规则的设计表格,用Ln(tc)表示,其中L为正交表的代号,n为试验次数,t为因素的水平数,c为列数,即能安排因素的最多个数[15]。对于表2的三因素三水平表,可按表3 所示的L9(34)正交表安排9次基于COMSOL软件的MAM单胞传声损失计算试验。
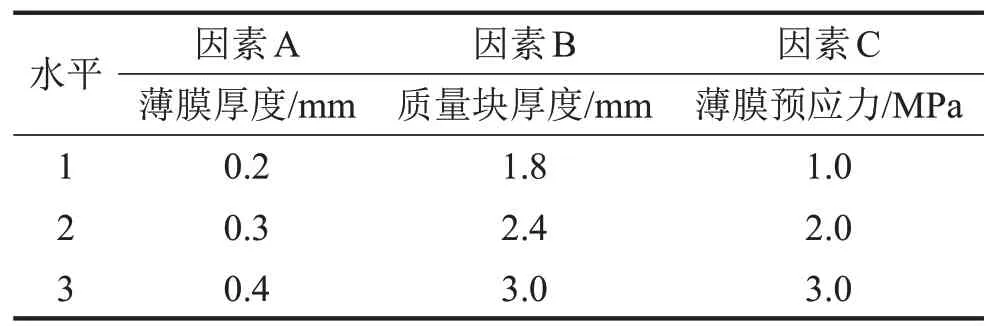
表2 正交试验设计优化因素水平表
以所考察的频率范围10 Hz~1 000 Hz 以内每隔10 Hz采集的传声损失值的平均值为隔声性能评价指标,根据模拟试验结果,算出MAM单胞的各因素所在列中相应因素水平对应的指标之和Kj以及各因素的极差R,并按照极差大小对影响因素进行排序,其结果列于表3中。
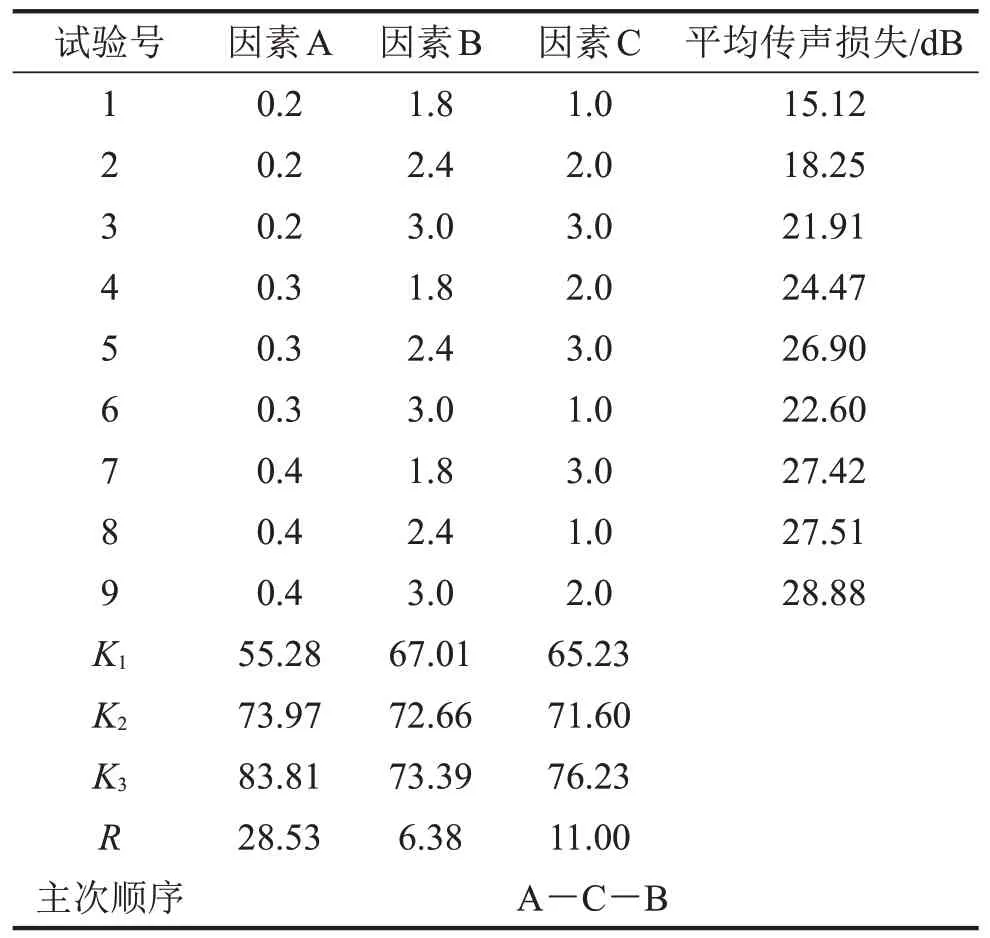
表3 L9(34)正交试验表
本文采用极差分析法分析正交试验结果,即将各因素所在列中相应因素水平对应的指标之和与各列结果的极差值,根据大小排列因素的主次顺序,并从中选出最优的组合。不同因素试验结果的极差反映了试验指标因为因素的改变而受影响的程度,极差值越大,则表明该因素水平值的改变对试验结果影响越大。
由表3 的计算结果可以看出,因素A,即薄膜厚度的极差值最大,说明薄膜厚度的改变对MAM 单胞隔声性能的影响最大,其次为因素C,即薄膜预应力的影响次大,最后是因素B,即质量块厚度的影响最小。
从表3中各因素所在列中相应因素水平对应的指标之和Kj可以看出,3个因素都在取第三水平值时获得最大指标之和,即获得最大平均传声损失。由此可知,使得MAM 单胞具有最佳隔声性能的参数值组合为A3B3C3,即薄膜厚度取为0.4 mm,质量块厚度取为3.0 mm,薄膜预应力取为3 MPa。根据此参数组合,计算MAM单胞参数优化后的传声损失,并与优化前根据表1 参数计算的传声损失对比,绘于图7中。
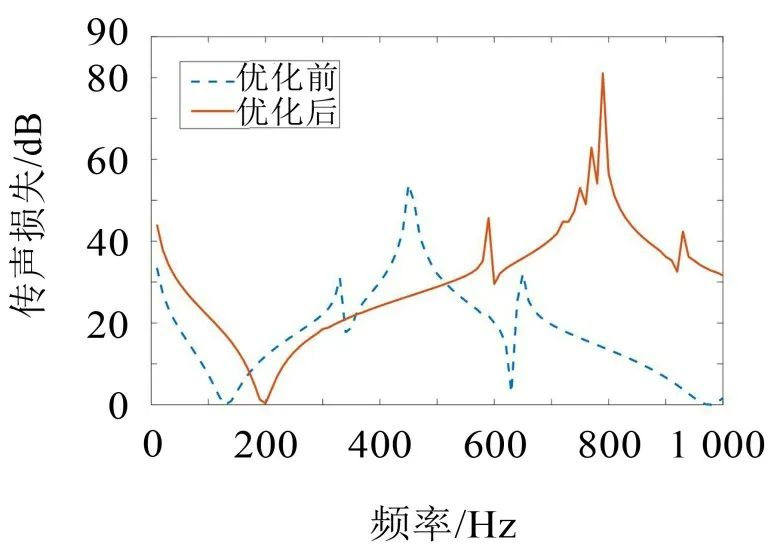
图7 正交优化前后MAM单胞的传声损失比较
由图7 可以看出,除180 Hz~510 Hz 频率范围外,设计参数经正交优化后的MAM 单胞的传声损失均明显大于优化前,整个传声损失曲线在1 000 Hz 以内的平均传声损失可达30.2 dB;优化后的MAM 单胞的传声损失峰值可达81.0 dB,比优化前的峰值53.8 dB高了50.5%。之所以在180 Hz~510 Hz频率范围内出现优化后的MAM单胞的传声损失低于优化前,是因为本研究以1 000 Hz 以内的平均传声损失为隔声性能评价指标,所以根据优化目标得到的设计参数并不能确保每一个频率段内的传声损失均大于优化前。
5 方形MAM单胞的组合应用研究
5.1 方形MAM单胞隔声特性
前面主要讨论了圆形MAM 单胞的隔声特性,为方便组合应用,本节针对方形MAM 单胞开展其隔声特性研究,并与圆形MAM 单胞的隔声特性进行对比分析。
图8 所示为边长100 mm(等于圆形MAM 单胞的直径)的方形MAM 单胞[14],其材料和结构参数与优化后的圆形MAM 单胞相同,仅将其框架和薄膜由圆形改成方形,膜中的预应力仍为3 MPa。
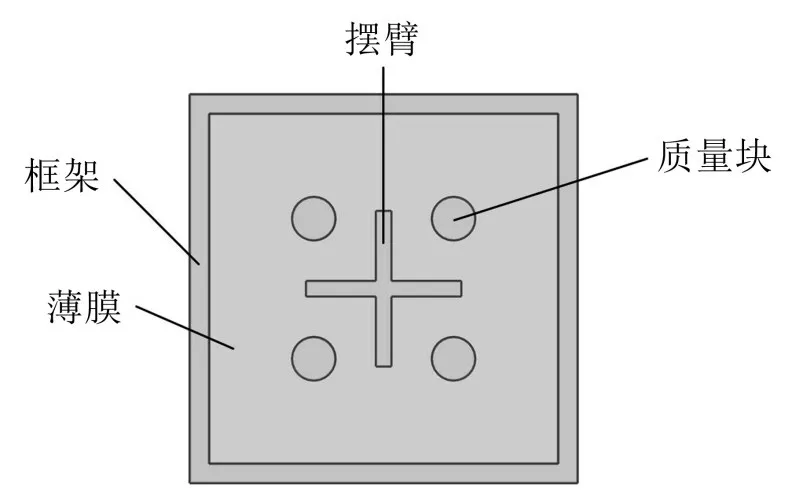
图8 MAM单胞结构示意图[14]
图9 展现了方形MAM 单胞与圆形MAM 单胞的传声损失对比曲线。
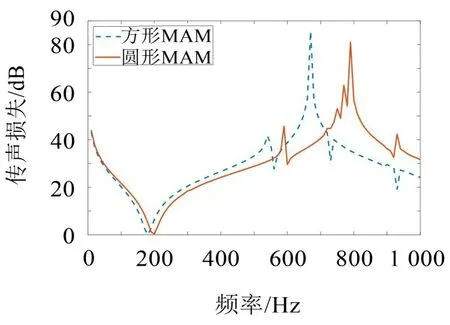
图9 方形、圆形MAM单胞传声损失比较
由图9可知,相对于圆形MAM单胞的传声损失曲线,方形MAM 单胞的传声损失曲线整体向低频移动,传声损失在670 Hz 处取得峰值85.5 dB,较圆形MAM 单胞的传声损失峰值高了4.5 dB,并且在190 Hz~700 Hz 以内,方形MAM 单胞的传声损失几乎都大于圆形MAM单胞,这说明方形MAM单胞具有更好的低频隔声性能。
图10(a)和图10(b)分别为利用COMSOL软件求解得到的方形MAM单胞传声损失曲线上第一个波谷值与最高波峰值所对应频率下的单胞振型。
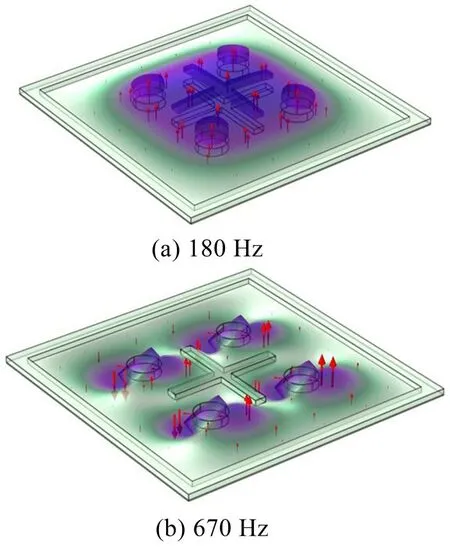
图10 方形MAM单胞的第1、9阶模态振型
由图10(a)可以看出,在频率为180 Hz 时,方形MAM单胞薄膜、4个质量块以及EVA摆臂整体均向上运动,意味着此时入射声波激励MAM 单胞产生了强烈的共振,整个单元的振动方向与声波同向,入射的声能没有被任何反方向声波抵消,声透射量最大,因此在图9 的传声损失曲线上产生了第一个波谷。由图10 (b)可以看出,方形MAM 单胞在频率670 Hz 时,4 个质量块在其横向同时表现出偶极子式的反共振模式,且摆动幅度很小。此时入射声能在薄膜上的4 个平衡区域被充分地抵消与转移,整个MAM单胞在入射声波与反射声波的共同作用下处于准动态平衡状态,振动能量无法向前传播,声透射量最小,因此在图9 的传声损失曲线上产生了最高峰值。
5.2 方形MAM单胞的组合应用
汽车前围板一般采用厚度约为0.8 mm的DC04钢板,为简便起见,不考虑在前围板上加工的孔洞,将前围板看作是一个无孔洞的完整钢板,并将由4个方形MAM单胞拼接而成的组合件安装于钢板一侧,探讨方形MAM单胞组合应用的隔声效果。
图11 所示为钢-方形MAM 前围板的声学仿真模型。将MAM单胞组合后的大框架、薄膜、钢板四周设为固定边界,薄膜预应力设为3 MPa。声场中的声学参数与声场边界设置与方形单胞的仿真设置一致。对仿真模型进行网格划分,取隔声频率计算范围为10 Hz~2 000 Hz,步长为10 Hz,通过仿真计算平面波通过钢-方形MAM 前围板的传声损失,并将其与0.8 mm 厚的单一钢板前围板的传声损失进行对比,其结果如图12所示。

图11 钢-方形MAM前围板仿真模型
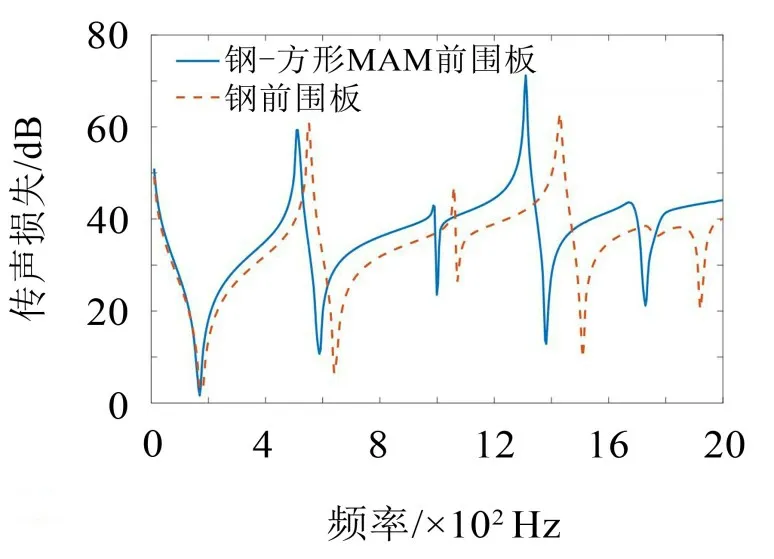
图12 钢-方形MAM前围板与钢前围板的传声损失
由图12 可以看出,与钢前围板相比,钢-方形MAM前围板的传声损失曲线向低频区域移动,且具有更大的传声损失峰值。在2 000 Hz以内,钢-方形MAM 前围板的传声损失峰值为71.2 dB,较钢前围板的62.9 dB高了8.3 dB,且钢-方形MAM前围板传声损失曲线最大峰值所对应的频率为1 310 Hz,较钢前围板低了120 Hz。由此可见,方形MAM 应用于传统的钢前围板上可以明显提高前围板的低频隔声性能。
6 结语
通过本文研究,主要得出以下结论:
(1)单一影响因素分析表明,随着薄膜厚度或薄膜预应力的增加,MAM单胞的传声损失曲线整体向高频区域移动,传声损失波谷处频率、波峰值及其所对应的频率均明显增大,MAM单胞的有效隔声频率范围变宽;改变质量块厚度,可以在某些频率范围内改变传声损失峰值及其所对应的频率;MAM单胞的传声损失受摆臂厚度变化的影响很小。
(2)多因素正交试验设计优化研究表明,薄膜厚度的改变对MAM 单胞隔声性能的影响最大,其次为薄膜预应力,最后是质量块的厚度;优化组合后的参数,可使MAM 单胞的平均传声损失达到30.2 dB,峰值传声损失81.0 dB 比优化前的峰值53.8 dB高了50.5%。
(3)在质量块、摆臂、薄膜状况等因素均相同的情况下,相较于圆形MAM 单胞,方形MAM 单胞具有更好的低频隔声性能。组合后应用于前围板的钢-方形MAM前围板可以明显提高传统钢前围板的低频隔声性能。
