基于FLAC3D的拉林铁路沿线风积沙液化特性研究

2021-12-15薛春晓孔令伟

铁道标准设计 2021年12期

崔雍，薛春晓，李舟，孔令伟

(中铁西北科学研究院有限公司，兰州 730030)

川藏铁路起于四川省成都市，经雅安、康定，昌都、林芝和山南，终于西藏自治区拉萨市，线路总长约1 629 km。拉林铁路是川藏铁路的重要组成部分，线路起于拉萨火车站，沿拉萨河而下，经贡嘎转向东，经山南、朗县、米林，跨越雅鲁藏布江到林芝站[1-2]。拉林铁路2012年3月列入国家《十二五综合交通运输体系规划》的快速铁路专栏，设计速度160 km/h，是国铁Ⅰ级单线电气化快速铁路。全长约433 km，与拉日铁路共线近33 km，新建里程近400 km。

新建拉林铁路位于青藏高原东南部，属于冈底斯山与念青唐古拉山、喜马拉雅山之间的藏南谷地，雅鲁藏布江中游，海拔在2 800～3 700 m。山高谷深，气候极端恶劣。面临的主要工程地质问题有：崩塌、滑坡、错落、泥石流、溜沙坡(又称碎屑流或岩屑坡)、水毁、冰害、风沙、高烈度地震与活动断裂、热害、高地应力(岩爆与大变形)等[3-7]。

拉林铁路沿线穿越多个地震带，地震活动强烈、大地震频发。此外，拉林铁路沿线风沙地段广泛分布，约占线路全长的10%以上，线路所经地区地形复杂、高差大、风向多变、山谷风作用强烈，路基工程所面临的高烈度区风积沙液化问题特殊而复杂。国内外学者虽然进行了一些研究，但由于拉林铁路部分区域地表被风积沙覆盖，且地下水位高、液化层颗粒比较细(如扎囊车站)，沙土性质完全不同于普通沙土，目前的研究成果只能起到一定的参考作用[8-15]。例如，陈文化等[16]对沙土液化产生的原因、影响因素和主要判别方法作了简要的回顾，并对近年来的研究现状进行了评述和对未来发展趋势提出了一些看法；牛琪瑛等[17]利用FLAC软件对水泥土桩加固的液化沙土地基建立模型并进行地震响应分析；吕西林等[18]应用FLAC软件对液化场地自由场体系的地震响应进行三维完全非线性分析，并与振动台试验结果进行了对比；郭英[19]基于有限差分软件，建立了能合理反映不同密实度未加固和水泥土桩加固液化土模型地基，分析比较了同一密实度条件下加固与未加固地基孔隙水压力、孔压比、竖向位移、表面加速度等的变化；王余庆等[20]利用等价非线性有效应力动力分析二维有限元程序，对饱和沙层的液化特点及砾石排水桩与地面压重的抗液化效果进行了分析。综上所述，基于FLAC3D技术开展川藏铁路高烈度区风积沙液化特性的研究具有重要的意义。

1 模型简介

1.1 模型尺寸和计算参数

沙土自由场的动力分析模型计算域尺寸为20 m×20 m×25 m，结合现场实际情况，将土层划分为3层，上层为粉土，中、下层为沙土，上、下层为非液化层，中层为可液化层，地下水位位于液化层表面，土层的计算参数见表1。

表1 模型土层计算参数

1.2 网格划分与边界条件

由于本次计算模型为规则的长方体，因此，数值模拟中采用了六面体网格(图1)。FLAC3D软件中提供了静止(黏性)边界和自由场边界两种边界条件来减少模型边界上波的反射。数值模拟中采用自由场边界，即主体网格的侧边界通过阻尼器与自由场网格进行耦合，自由场网格的不平衡力施加到主体网格的边界上。由于自由场边界提供了与无限场地相同的效果，因此，向上的面波在边界上不会产生扭曲。

图1 施加自由场边界条件的网格

1.3 孔压模型

在FLAC3D软件中主要有Finn模式和Byrne模式两种塑性体积应变增量公式，本次数值模拟采用建立在摩尔-库伦模型基础上的Finn模式，它反映了孔压在地震动作用下的累积效应，此外，该模式假定动孔压的上升与塑性体积应变增量相关。基本原理为：当沙的密度和往返作用次数一定时，体应变与竖向静正应力无关，只取决于往返剪应变幅值；当往返剪应变幅值一定时，体应变随往返作用次数的增加而增加。每一次往返作用引起的体应变增量取决于已经产生的永久应变数值和即将作用在土体上的剪应变幅值。假设即将作用的剪应变为第N次，那么第N次产生的永久体应变增量与之前已经产生的永久体应变关系可用下式表示

(1)

式中，Δεv，d为第N次产生的永久体应变增量；γ为第N次作用的剪应变幅值；εv，d为第N次往返作用以前已经产生的永久体应变；c1=0.8，c2=0.79，c3=0.45，c4=0.73。

1.4 模拟工况

为较为深入地了解研究区饱和沙土的动力特性，以及各种因子对动力特性的影响，沙土自由场模拟总计14种工况，各工况的计算参数见表2。研究区段位于8度烈度区，地震动峰值加速度为0.30g。

表2 自由场模拟各工况参数

2 风积沙液化特性及影响因素

2.1 自由场液化特性分析

孔压比是在循环应力作用下沙土的孔隙水压力增量与侧向有效固结应力的比值，可在一定程度上反映沙土的液化趋势，自由场中孔压比越接近于1.0，说明该区域沙土越容易液化。图2为工况3条件下自由场的超孔压比分布云图，从图2不难看出，可液化层大部分区域的孔压比在0.9以上，表明在地震动环境作用下研究区可液化沙土的大部分区域存在液化的可能，需根据预测的地震烈度进行处理才能保障该地基上建筑物的安全。此外，值得注意的是毗邻非液化层的可液化沙土(简称毗邻层，下文相同)孔压比明显偏小，说明非液化土层对相邻的可液化土层液化具有一定的抑制作用。

图2 自由场的超孔压比云图

为更直观地分析可液化层中饱和沙土的液化趋势，提取工况3土层中的超孔压比时程曲线(图3)，可以看出，可液化沙土中各深度处孔压比变化趋势基本一致，大致可分为两个阶段：急剧上升阶段和振荡平稳阶段，曲线拐点大致在1～2 s。但受邻近非液化土层及埋深的影响，曲线在细节上存在差异。除毗邻层以外，其余各层的孔压比均达到了1.0，但各土层孔压比峰值到达时间明显不同，深度越大孔压比达到峰值所需时间越长，说明饱和沙土的液化并非同时到达，而是上部土层首先液化，之后才是中、下部土层。

图3 可液化沙土超孔压比时程曲线

相关研究表明，松散的沙土在振动作用下，沙颗粒将会重新排列，导致土体密实度增加，从而会产生一定的沉降。因此，探索可液化沙土在振动环境下的沉降规律，可为液化地基上建筑物的沉降控制提供指导。图4为工况3条件下不同埋深监测点土体的沉降时程曲线，不难发现，在动力作用前期，振密后的土体沉降迅速增大，待土体达到一定密实度后，土层沉降速率逐渐减小，沉降曲线随时间趋于平缓。此外，注意到不同土层的沉降存在差异，埋深越浅，沉降量越大。

图4 可液化沙土竖向位移时程曲线

2.2 加速度对自由场液化特性的影响

地震动加速度不仅能反映地震的烈度，也可以在一定程度上预估地震损失。了解不同加速度条件下的地震动，可以为地基抗震方案提供依据。图5为不同加速度条件下自由场的超孔压比云图，从图5可以发现，随着地震动加速度的增大，孔压比在0.9～1.0的区域(简称高孔压比区域，下同)在逐渐扩大。上述现象说明，同等条件下，加速度越大地震动的能量越高，可液化沙土的液化范围越大，对地基上的建筑物影响也越大。此外，值得注意的是毗邻层的范围随着加速度增加呈递减趋势，说明随着加速的增大非液化层抑制沙土液化的作用在逐渐减弱。

图5 不同加速度条件下自由场的超孔压比云图

图6为不同加速度条件下可液化沙土孔压比时程曲线，可以看出，孔压比随时间的变化趋势基本一致，即均存在急剧上升阶段和振荡平稳阶段，但拐点的位置明显不同。随着加速度增加，曲线上拐点的位置逐渐向右移动，即达到孔压比峰值的时间越长。说明加速度越大，同等条件下研究区沙土液化所需的时间越短。此外，还可以看出，加速度amax=0.05g时，仅深度3 m处的孔压比峰值达到了1.0，而加速度amax=0.10g，0.20g，0.30g时，深度3～7 m时均达到了1.0。表明加速度较小时，虽然沙土可能达到液化状态，但液化的区域较小。

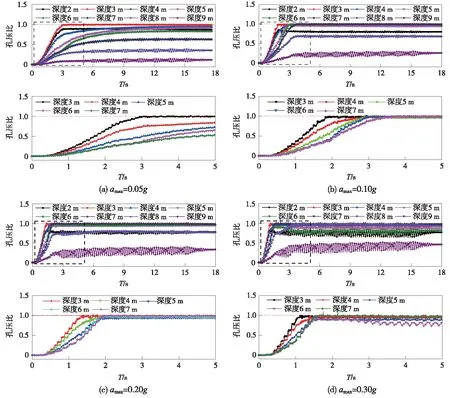
注：图6(a)～图6(d)中的下图为虚线框中局部放大图

地震作用下，越靠近地表，竖向位移越大，故提取地表的竖向位移进行分析。图7为不同加速度条件下地表竖向位移时程曲线，不难发现，随着地震动加速度的增大，地表最终竖向位移呈递增趋势。主要原因在于：外界加速度越大，地震动蕴涵的能量越高，在同等条件下沙土振的越密实，从而使得同一位置的竖向位移越大。

图7 不同加速度条件下地表竖向位移时程曲线

2.3 频率对自由场液化特性的影响

地震动频率是影响沙土液化的关键指标，研究它对液化特性的影响对地基抗液化具有指导作用。图8为不同频率条件下自由场的超孔压比云图，可以看出，高孔压比区域范围随着频率的增大而逐渐扩大，说明频率在3～6 Hz内，地震频率越高，沙土可能液化的范围在逐渐增大。

图8 不同频率条件下自由场的超孔压比云图

图9为不同频率条件下可液化沙土自由场的超孔压比时程曲线，不难看出，各种频率下孔压比的变化趋势基本一致，但曲线的拐点存在差异，频率越小曲线的拐点越靠左，说明频率越小达到孔压比峰值所需的时间越短，即在3～6 Hz内，频率越大地震液化所需时间越长。此外，注意到地震频率越大，各层土体达到液化时的时间差越大，即下层土体液化的滞后性越强。

注：图9(a)～9(d)中的下图为虚线框中局部放大图

图10为不同频率条件下可液化沙土自由场地表竖向位移时程曲线，分析变化趋势不难看出，位移随着时间的推移呈波动递增趋势，但各频率条件下最终的竖向位移量存在差异。在频率3～6 Hz内，随着地震频率的增大，可液化沙土的最终竖向位移呈递增趋势。在频率6 Hz时，最终竖向位移约5 cm，而频率3 Hz时，最终竖向位移约1.8 cm，前者竖向位移约为后者的3倍。

图10 不同频率条件下可液化沙土自由场地表竖向位移时程曲线

2.4 液化层厚度对自由场液化特性的影响

图11为不同液化层厚度条件下自由场的超孔压比云图，厚度H对可液化沙土液化的影响显著。随着液化层厚度增加，高孔压比区域由连续片状分布逐渐分离为两部分，且厚度越大两部分之间的距离越大。此外，注意到中间层的超孔压比在0.8～0.9，略小于上下两层。

图11 不同液化层厚度条件下自由场的超孔压比云图

图12为不同液化层厚度条件下地表竖向位移时程曲线，趋势显示竖向位移随着时间的推移呈波动递增趋势，并最终趋于稳定。此外，随着液化层厚度增大，表层的最终竖向位移呈递增趋势。厚度为13 m时，最终竖向位移约为8 cm，而厚度为7 m时，最终竖向位移约为4 cm，前者竖向位移约为后者的2倍。

图12 不同液化层厚度条件下地表的竖向位移时程曲线

2.5 液化层埋深对自由场液化特性的影响

图13为不同埋深条件下自由场的超孔压比云图，可以看出，埋深对可液化沙土的液化趋势影响非常显著。当埋深由2.5 m增加至3.5 m时，高孔压比区域由连续片状分布逐渐分离为两部分；当埋深由3.5 m增加至4.5 m时，上层高孔压比分布区域呈递减趋势；当埋深增加至5.5 m时，上层高孔压比区域几乎消失。上述现象揭示了上覆土层厚度对可液化沙土的液化具有抑制作用，土层厚度越大抑制作用越显著，这说明，可通过增加上覆土层的压力来减小可液化层的液化趋势。