直接分析法在高耸钢结构塔架设计中的应用

艾 虎

（中冶南方都市环保工程技术股份有限公司，湖北 武汉 430205）

钢结构具有高强、轻质、塑性韧性好等优点，但是其稳定性问题会影响结构整体安全性。目前各国规范主要采用基于有效计算长度系数的方式来考虑结构稳定性。采用基于有效计算长度系数设计的构件，可能存在某些杆件应力比实际情况大，有些构件应力比实际情况小的问题，结构可能存在一些安全隐患。对更加复杂的空间结构，例如高耸的钢结构塔架，确定每根杆件的有效计算长度系数，这个过程不仅烦琐，而且也不一定准确。同时，该方法也存在一定的不合理性，如结构内力分析模式与构件承载力计算模式不一致，不能考虑内力重分布等。面对日益复杂的结构体系，传统有效长度系数计算法已不能满足现代结构设计的需求，必须对结构进行一次全过程的整体分析，综合考虑影响结构承载力的各种非线性因素和缺陷，进而预测结构的破坏模式和极限承载力。该文以某脱硫塔高耸塔架为例，分别采用新钢标给出的三种分析方法，对塔顶位移、塔底角柱反力、塔身不同高度部位杆件的稳定应力比进行了计算分析对比。

1 新钢标给出的三种分析方法

1.1 一阶弹性分析法

根据未变形的结构建立平衡条件，不考虑结构位移对内力产生的影响。此时，变形和荷载的关系是线性的。

在完成结构整体分析后，通过控制长细比、构件稳定应力等来设计构件截面。

1.2 二阶分析法

二阶分析法即对结构内力与变形，考虑二阶效应的影响。结构在荷载作用下，将产生一定的变形，该变形将会在结构中引起附加内力，附加内力将使结构产生进一步的附加变形，这种附加变形又将在结构中引起一定的附加内力，如此重复作用直到产生的附加效应很小为止。此时，变形和荷载呈现非线性的关系。

根据《钢结构设计标准》（GB 50017-2017）的相关规定，二阶p-Δ分析应考虑结构整体初始几何缺陷的影响[1]。

对如何计算结构整体初始几何缺陷，规范给出了具体做法—通过在每层柱顶施加假想等效水平力Hni方式来考虑结构整体初始几何缺陷。假想水平力可按式（1）计算，施加方向应考虑荷载的最不利组合[1]。

式中：Hni—第i层楼的假想水平力（N）；Gi—第i层楼的总重力荷载设计值（N）；ns—结构总层数。

1.3 直接分析法

二阶p-Δ分析法只是考虑了结构水平位移对竖向力的效应，并没有考虑杆件挠度（初始弯曲）对轴力作用的效应。事实上，杆件在生产、加工、运输、焊接过程中，也会存在一定的缺陷。为补齐该效应，《钢结构设计标准》（GB 50017-2017）给出了直接分析法。直接分析法是对二阶p-Δ分析法的进一步完善。

根据《钢结构设计标准》（GB 50017-2017）的相关规定，直接分析同时考虑p-Δ效应、结构整体初始几何缺陷、构件的初始几何缺陷和残余应力的影响。结构整体初始几何缺陷按照式（1）的方式考虑，构件的初始缺陷采用假想均布荷载进行等效简化计算，假想均布荷载按式（2）确定[1]。

式中：l—构件的总长度（mm）；q0—等效分布荷载（N/mm）；e0—构件中点处的初始变形值（mm）；Nk—构件承受的轴力标准值（N）。

2 三种设计方法在高耸钢结构塔架设计中的应用对比

某钢厂烟气治理工程，采用湿法脱硫工艺，下部脱硫塔为自立式结构，上部烟囱承托在塔架上，承托的位置分别位于49m和77m，塔架总高98.2m，0m～31.5m，塔架平面尺寸为16m×16m，31.5m以上采用变截面，塔顶处塔架平面尺寸8.6m×8.6m。塔架除承担烟囱荷载外，还承担脱硫塔和烟囱传来的风荷载。项目位于8度区，地震加速度0.20g，设计地震分组为第二组，基本风压0.45kN/m2。塔体的三维视图见图1。

图1 塔体三维视图

高耸结构与地震作用组合相比，风荷载组合起控制作用。因此，顶部位移计算采用标准组合：1.0×恒载+1.0×风载+0.7×活载；塔底角柱反力以及塔身不同高度部位杆件稳定应力计算采用基本组合：1.3×恒载+1.5×0.7×活载+1.5×风载。

2.1 塔顶位移比较分析

对比表1中数据和规范限值，三种方法计算得到的塔顶位移均满足《高耸结构设计标准》中Δu/H≤1/75的要求[3]。另外，考虑p-Δ效应、结构整体初始几何缺陷、构件的初始几何缺陷和残余应力的影响等对该工程钢塔架的水平位移的影响基本可以忽略。

表1 塔顶位移

2.2 塔底角柱反力比较分析

从表2中数据，可以看到，通过在每层柱顶施加假想水平力Hni等效考虑结构整体初始几何缺陷的做法，对柱底反力的影响基本可以忽略。

表2 塔底某角柱反力

2.3 塔架角柱不同标高段的稳定应力比比较

对该柱第一段，杆件截面Φ500×12mm，柱高范围0.000m～15.500m。按照有效计算长度系数法计算的长细例如下。

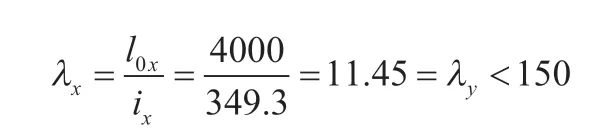
式中：λx、λy—构件x方向和y方向的长细比；l0x—构件对截面主轴x的计算长度（mm）；ix—构件截面对主轴x的回转半径（mm）。

对该柱第二段，杆件截面Φ450×12mm，柱高范围15.500m～32.500m。按照有效计算长度系数法计算的长细例如下：

对该柱第五段，杆件截面Φ402×10mm，柱高范围41.000m～49.000m。按照有效计算长度系数法计算的长细例如下。

对该柱第六段，杆件截面Φ325×9mm，柱高范围70.000m～77.000m。按照有效计算长度系数法计算的长细例如下。

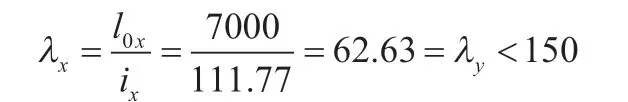
从表3～表6中数据，可以看到采用一阶分析法和二阶分析法，对角柱在0.000m～49.000m，稳定应力比的影响差别不大，采用直接分析法，总应力比比采用一阶分析法分别大4%、0.7%、3.3%，而且轴向应力明显下降，但是由弯矩产生的应力明显增加；对角柱在70.000m～77.000m，稳定应力比的影响差别相对明显，采用直接分析法的总应力比比采用一阶分析法减小15.7%，差值超过10%，主要原因为本段柱计算长度较长为7m，长细比相对偏大，但是该柱承担的轴力较小（相对杆件截面大小而言），二阶效应总体可控。

表3 塔架某角柱稳定应力比一

表4 塔架某角柱稳定应力比二

表5 塔架某角柱稳定应力比三

表6 塔架某角柱稳定应力比四

2.4 塔架不同部位支撑稳定应力比比较

对承托最上部烟囱位置的支撑杆件，杆件截面Φ180×6mm，标高范围77.000m～84.000m。按照有效计算长度系数法计算的长细例如下。

对承托最上部烟囱位置的支撑杆件，杆件截面Φ194×7mm，标高范围70.000m～77.000m。按照有效计算长度系数法计算的长细例如下：

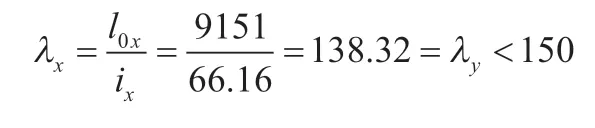
对承托第二节烟囱位置的支撑杆件，杆件截面Φ194×7mm，标高范围49.000m～56.000m。按照有效计算长度系数法计算的长细例如下：

对塔架最下部位置的支撑杆件，杆件截面Φ245×7mm，标高范围0.000m～7.500m。按照有效计算长度系数法计算的长细例如下：

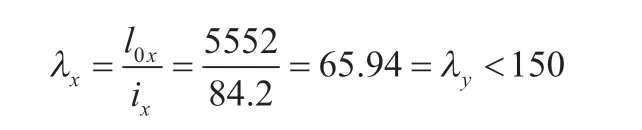
从表7～表10中数据，可以看到采用一阶分析法和二阶分析法，对支撑构件的稳定应力比计算结果影响差别不大，但是采用直接分析法，总应力比比采用一阶分析法分别减小38%、36%、38%、2%，而且轴向应力明显下降，但是由弯矩产生的应力明显增加，杆件自身的挠曲二阶效应比较明显。承托烟囱竖向荷载的77m处上、下部位的支撑以及承托烟囱竖向荷载的49m处上部支撑，由于计算长度较长，分别为8.9m、9.2m、10.0m，采用直接分析法后，稳定应力比下降明显。0.000m～7.500m处支撑，由于计算长度相对较短（5.6m），长细比相对较小，采用直接分析法，稳定应力下降不明显[5]。

表7 塔架某支撑稳定应力比一

表8 塔架某支撑稳定应力比二

表9 塔架某支撑稳定应力比三

表10 塔架某支撑稳定应力比四

3 计算结果对比分析

通过在每层柱顶施加假想水平力Hni等效考虑结构整体初始几何缺陷的做法，对结构顶部水平位移、对基础设计的影响可以忽略。

该塔架虽然属于高耸结构，但是：a、塔架的高宽比6.1375，接近6（《高层民用建筑钢结构技术规程》里结构适用的最大高宽比要求[2]，结构的刚度、整体稳定性等方面是相对比较合理的；b、塔架是完全开敞的结构，无维护结构，整体承受的风荷载（横向荷载之一）比较小；c、塔架仅承托上部烟囱的重量，塔架整体承担的竖向荷载相对也小，结合二阶效应的假想水平力公式看，根据总重力荷载设计值折算来的水平荷载相对也小；三个因素叠加后，对该塔架采用一阶分析法、二阶分析法或者直接分析法进行设计，结果总体差别不大。

相比于塔架4根角柱，二阶效应对支撑的影响更大，尤其是计算长度较大、荷载较大的支撑杆件。

该塔架四角角柱，应力比较小，按照直接分析法的计算结果，可以对杆件截面进行优化。

3 结论

该文采用《钢结构设计标准》提供的三种分析方法，运用SAP2000软件对某实际工程的高耸钢结构塔架进行了计算和对比分析，相比于一阶分析法：1）二阶分析法和直接分析法对所有柱子取有效长度系数1，避免了计算系数在一些高耸塔架等结构中的复杂性和不确定性，减少设计人员的错误。2）直接分析法对结构内力提供了更精确的计算方法。在高耸钢结构塔架杆件的内力计算中，直接分析法包括了结构和构件初始几何缺陷的影响和稳定性的影响，而一阶弹性分析法和二阶分析法则不能。承受竖向或者轴向较大荷载且计算长度较长的支撑构件以及整个结构，尤其应考虑结构和构件初始几何缺陷的影响。通过直接分析法的计算、分析，可以得到更精确的杆件应力和变形，进而可以充分发挥杆件的截面特性等。尽管如此，在该范围内，一阶弹性分析法仍然是可接受的方法。3）对高耸塔架设计，应注意其高宽比。合理的高宽比，有利于结构整体刚度、整体稳定以及经济性[2]。

稳定性是钢结构设计的重点，二阶效应又是稳定性的根源，工程师有必要按照规范的要求，对承受竖向荷载较大，部分杆件长细比较大的框架、支撑框架、高耸结构等，适时考虑二阶分析设计。直接分析法不仅能提高计算的精确度，而且可以弥补高耸塔架类结构一阶分析和二阶分析的不足，得到的结果更为合理、更有说服力[4]。