大功率IGBT器件及其组合多时间尺度动力学表征研究综述*
2021-12-14马伟明罗毅飞刘宾礼贾英杰
肖 飞,马伟明,罗毅飞,刘宾礼,贾英杰,李 鑫
(海军工程大学 舰船综合电力技术国防科技重点实验室, 湖北 武汉 430033)
现代大容量电力电子装置和系统是一种多时间尺度的电力电子混杂系统,其中,全控型电力电子器件——绝缘栅双极晶体管(Insulated Gate Bipolar Transistor,IGBT)是实现高性能电能变换与控制的核心部件,它一方面可以保证电能变换装置具有良好的动、静态性能,另一方面可以降低整个装置的体积、成本、噪音和减少维护等。IGBT综合了金属-氧化物半导体场效应晶体管(Metal-Oxide-Semiconductor Field-Effect Transistor, MOSFET)和双极结型晶体管(Bipolar Junction Transistor,BJT)的结构,具有驱动简单、功率等级高、功耗小、热稳定性好等优点,被广泛应用于各种中、大功率电力电子装置中。
电力电子器件及其组合混杂系统包含各种不同时间尺度运行的器部件,其工作状态、机理描述以及电、磁、热等特性均表现出复杂的动力学行为。既有单个器件的开关瞬态载流子运动的纳秒级过程,又有组合开关的微秒级过程,同时也有贯穿始终的热传递过程;既有器件内部物理关系,又有器件与其他连接部件及其组合之间的耦合关系。目前的电力电子混杂系统装置应用设计中大多还未考虑多时间尺度下核心功率半导体器件瞬态动力学特性及其耦合关系,遵循的是静态或准静态设计准则与方法,难以实现系统的精确设计,无法保证全工作边界内系统的性能与安全,难以克服经济性与可靠性之间的矛盾。因此,迫切需要查明电力电子器件及其组合混杂系统多时间尺度的动力学表征方法,为电力电子装置的精确、可靠设计提供器件层面的支撑。
目前,国内外对大功率电力电子器件及其组合多时间尺度动力学表征的研究还不多,近几年才逐步兴起,主要包括三个方面。①多时间尺度电热耦合建模:传统电力电子系统设计针对不同层面的需求,可将器件模型分为四类——行为模型、物理模型、数值模型以及混合模型[1]。建立了场终止型IGBT的载流子级开关瞬态模型[2-3],同时实现了平面栅与沟槽栅结构的统一建模[4];建立了PIN功率二极管的改进物理模型[5-6],可实现二极管开关瞬态以及极端工况例如夹断现象的模型表征;针对装置输出周期时间尺度,通过对模型的简化,实现了大时间尺度例如毫秒级的器件组合仿真,将复杂模型应用于复杂电路仿真中[7-8];将电气和传热模型进行耦合,建立了不同时间尺度结温预测模型,实现了针对不同对象、不同应用工况的器件组合结温的有效评估[9-10]。②失效量化评估:以可靠性为目标的电力电子系统设计和研究也越来越受到重视[11],这对功率半导体器件模型提出了新的需求。早期研究基于半导体物理对续流二极管开关瞬态浪涌电流能力进行了分析[12];对IGBT瞬态电击穿失效进行了研究,查明了器件的瞬态电热击穿失效机理,但缺乏对边界的准确刻画[13];提出了一种基于热平衡分析的器件极限应用评估方法[14];从材料的角度对IGBT模块焊料层疲劳和键合引线疲劳导致的器件失效机理进行了分析,实现了器件寿命评估从定性和基于数理统计的粗略评估[15-16]到基于材料微观特性和模块端口特征量变化的精细评估[17-18]的提升,并逐步向装置中的器件可靠性精确量化评估推进。③混杂系统多速率仿真方法:主要针对目前电力电子器件仿真分析所采用的路-路耦合、场-场耦合以及场-路耦合三种仿真模式。通过热-电比拟的思想将阻容(Resistion-Capacitor, RC)热网络引入Spice、Saber等电路仿真平台,构建了基于路-路耦合的电热仿真方法[19-20],具有计算效率高的优势;场-场耦合方法基于有限元法(Finite Element Method, FEM)实现,可对IGBT的温度、应力特性进行精确求解,但仿真效率低且较难对电气特性进行准确的表征[21-23]。场-路耦合基于电路与热场的联合仿真,可兼顾电路仿真的高效和FEM仿真的高精度等优势,例如热仿真软件Icepak与电路仿真软件Simplorer的联合,但作用过程是单向的[24];文献[25-26]提出基于Pspice-Comsol的场-路双向耦合多速率仿真方法,实现了电气特性和温度、应力场的高效仿真。
因此,国内外在电力电子器件多时间尺度动力学表征研究方面,取得了一定的进展和成果,研究仍在持续开展中。本文着眼于电力电子器件基础研究及其对电力电子装置的应用支撑,以IGBT为例,从器件的建模方法入手,再到基于模型的失效量化评估以及关键仿真方法,最后实现对装置可靠设计的支撑,系统阐述了大功率IGBT及其组合多时间尺度动力学表征方法,可为电力电子混杂系统的精确设计提供器件层面的理论指导和技术支撑。
1 大功率IGBT及其组合多时间尺度电 热瞬态建模
由于电力电子系统的多时间尺度特性,其核心开关器件的工作表现出复杂的多物理场耦合特性,如图1所示,不同物理场又表现出不同的时间尺度特性。

图1 IGBT器件工作复杂多物理场耦合作用Fig.1 Multiple physics fields coupling of IGBT operation
针对这一特点,作者团队提出了采用多时间尺度建模的思想,以IGBT为例建立了器件及其组合多时间尺度电热瞬态模型,实现了瞬态特性的精确表征。建模包括电气建模和传热建模。多时间尺度电气模型由表征时间尺度的不同,可分为针对开关瞬态的纳秒至微秒级时间尺度,用于精确表征器件瞬态过程;针对电能变换装置输出周期的微秒至十毫秒级时间尺度,用于表征器件在输出周期内的关键特性,例如电压、电流尖峰。多时间尺度传热模型由于表征时间尺度的不同又可分为针对器件开关瞬态的百纳秒至微秒级时间尺度、针对器件开关周期非稳态的毫秒级时间尺度以及针对电能变换装置输出周期稳态秒级时间尺度。
1.1 IGBT多时间尺度电气建模方法
1.1.1 纳秒至微秒级瞬态电气建模
IGBT可以看作是金属-氧化物半导体(Metal-Oxide-Semiconductor, MOS)和BJT的复合结构,典型场终止型IGBT结构如图2所示,其运行特性本质上是由内部载流子的激发和运动决定的[27]。因此,IGBT纳秒至微秒级瞬态电气建模,针对的是器件内部载流子运动的瞬态特性表征,一般采用的是基于半导体物理的建模方法,也称为物理模型。
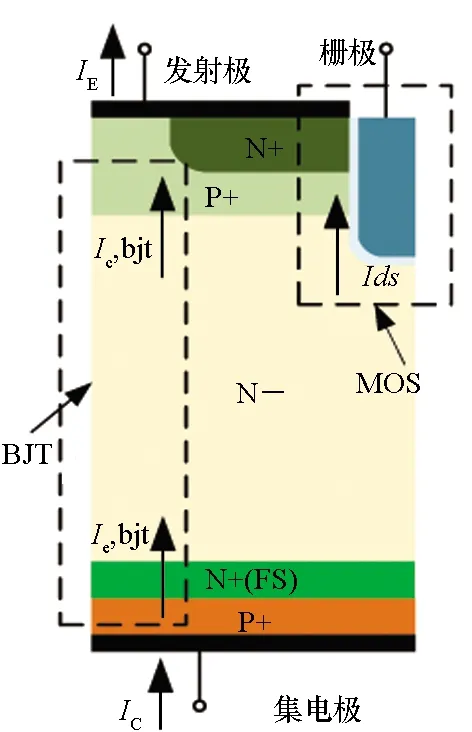
(a) IGBT物理结构(a) Physical structure of IGBT

(b) IGBT等效电路(b) Equivalent circuit of IGBT图2 IGBT物理结构及其等效电路Fig.2 Physical structure and equivalent circuit of IGBT
物理模型的建模原理是基于载流子运动和分布的基本方程:电流密度方程和载流子连续性方程[28]。电流密度方程如式(1)所示,即总电流由漂移电流和扩散电流组成。
(1)
载流子连续性方程如式(2)所示,即载流子电荷变化与产生电流、复合电流和扩散电流有关。
(2)
基于式(1)和式(2),可得到基区载流子双极扩散方程(Ambipolar Diffusion Equation, ADE),在基区大注入条件下,可简化为如下形式[23]:
(3)
通过对ADE的求解,得到载流子分布和运动特性,进而得到电流和电压的瞬态特性。因此,物理建模的核心是求解ADE。根据求解方法的不同,作者团队将现有物理建模归纳为形函数法、空间变换法、时间变换法以及集总电荷法[29]。
1)形函数法
形函数法是基于载流子稳态分布,再叠加动态扰动,建立载流子的近似分布,然后代入ADE进行模型的求解。具有代表性的是Hefner模型和Kraus模型,它们的区别主要表现在暂态过程求解中使用形函数的不同。
Hefner模型使用式(4)所示一阶线性分布来描述开关瞬态载流子在基区内的分布[30]。
(4)
Kraus模型[31]采用式(5)多项式拟合开关瞬态基区过剩载流子分布。暂态过程更为精确,但拟合参数多,模型计算量和使用难度增大。
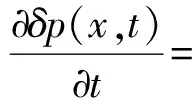
(5)
Hefner建模方法由于忽略瞬态过程基区载流子复合,对高压宽基区器件的表征存在较大误差[28]。为此,国内学者将二维Hefner模型扩展为三维模型[32],作者团队也对Hefner模型进行改进,考虑基区瞬态载流子复合,实现了高压IGBT开关特性的准确表征[2-3],如图3所示。
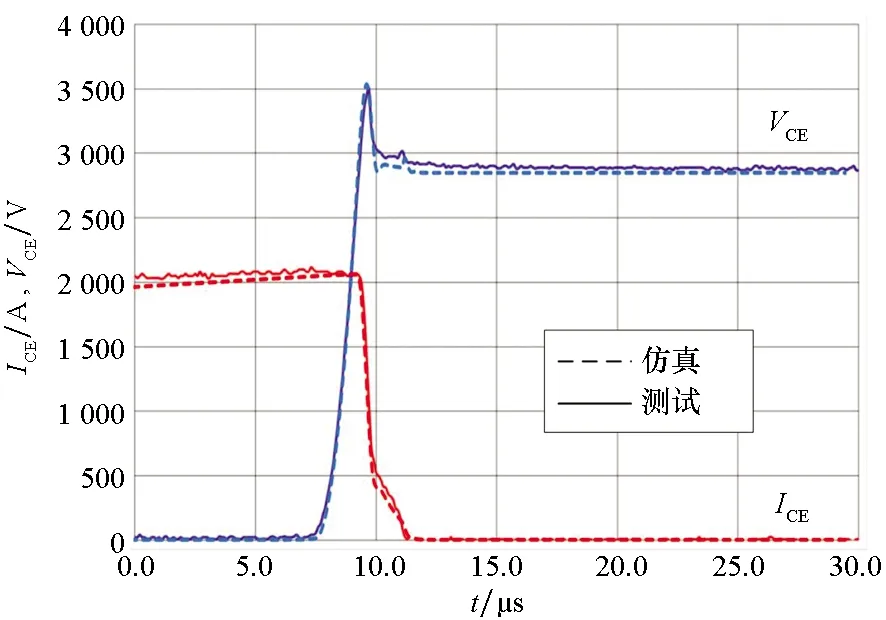
(a) 关断瞬态波形(a) Turn-off transient waveforms

(b) 开通瞬态波形(b) Turn-on transient waveforms图3 高压压接型IGBT改进Hefner模型瞬态仿真[2]Fig.3 Transient simulation of high voltage press pack IGBTs with optimized Hefner model
英飞凌也提出一种改进的Hefner模型[33],将IGBT基区载流子分布采用分区形函数进行表征,提高了模型精度,但也大大增加了模型复杂度和参数提取数量,限制了模型的应用。
形函数法能够表征器件的物理机理,同时也可以在仿真效率与精度中取得较好的折中。
2)空间变换法
空间变换法是对空间变量x进行级数变换来近似求解ADE[34],如傅里叶级数求解方法:
(6)
系数Pk(t)可等效为图4所示串联RC网络中的电压Vk进行求解。国外Palmer等、国内Xue等采用该方法,建立了IGBT模型[35-36]。

图4 求解傅里叶分解系数的等值RC网络Fig.4 Equivalent RC network for solving the coefficient of Fourier transform
空间变换模型可根据仿真精度和计算量要求合理选择k值,但该方法较为复杂,模型参数多且提取困难,无法反映IGBT内部物理特性。
3)时间变换法
时间变换法是对时间变量t进行级数变换以求解ADE。利用IGBT稳态边界条件求解基区载流子分布,再代入电流密度方程,求得基区集电极边缘处电流,如式(7)所示,再利用Pade多项式近似表示成图5的等效电路进行求解[37]。
(7)
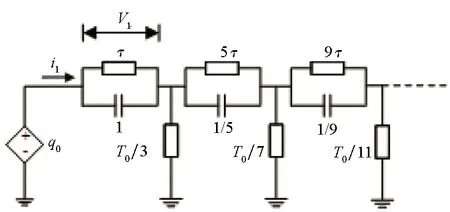
图5 拉普拉斯变换法等效电路Fig.5 Equivalent circuit of Laplace transform
Strollo首先应用该方法建立了IGBT和二极管物理模型[37]。
时间变换模型的精度和复杂度均与等效电路的阶数有关,且变换后也不能反映内部物理特性。因此,也没有得到广泛应用。
4)集总电荷法
集总电荷法是对IGBT基区进行分区,将各区域内电荷浓度等效为该区域内一个点的电荷浓度,各个点的电荷浓度之间近似认为线性分布,再利用KCL和KVL建立这些集总电荷点之间的关系来表征载流子在基区内的分布和运动,如图6所示。由于集总电荷法不用求解ADE,而是直接将基区电流表示成空穴电流和电子电流的形式,因此,收敛性更好,如式(8)所示。
(8)
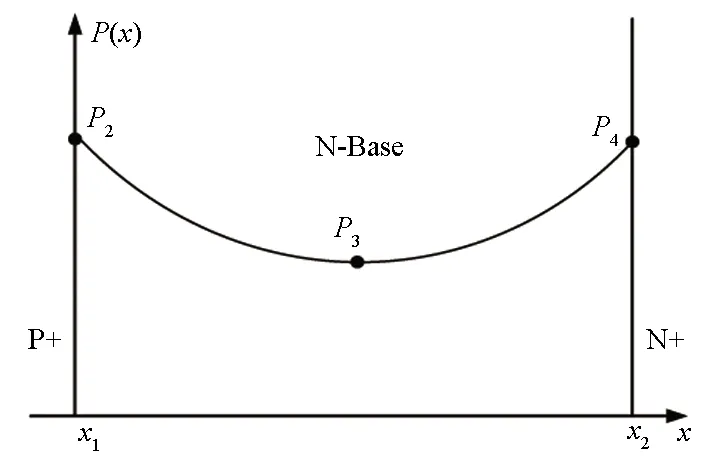
图6 传统集总电荷模型分区Fig.6 Subregion of the traditional lumped charge model
该方法由Lauritzen等提出,由Iannuzzo等应用于IGBT的建模[38]。
传统集总电荷法采用了有限节点数的简化,精度一般。为此,作者团队提出了一种新的集总电荷建模方法,将点电荷转变为体电荷来代替区域内的电荷浓度,重新定义了集总电荷电流,显著提升了模型精度[39],如图7所示,图7中彩色部分面积与虚线和坐标轴围成的面积之差为集总电荷模型误差。
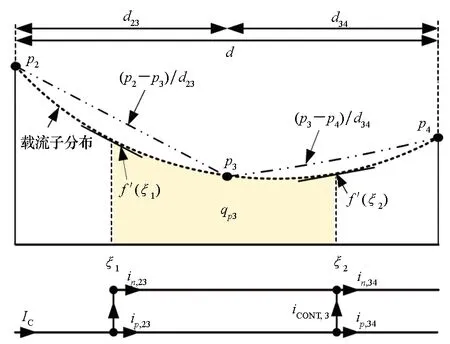
(a) 传统集总电荷模型(a) Traditional lumped charge model
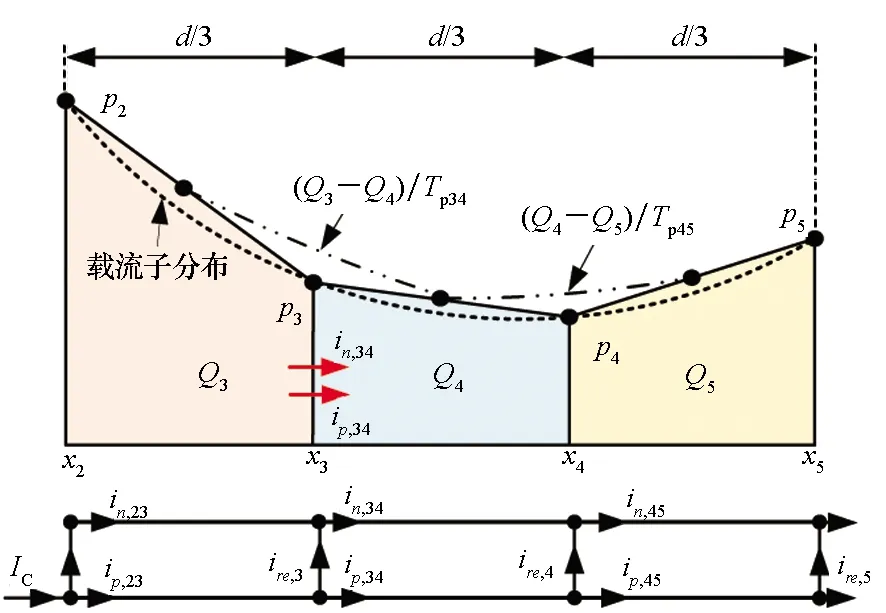
(b) 新集总电荷模型(b) New lumped charge model图7 集总电荷模型误差对比Fig.7 Simulation error comparison
上述四类物理建模方法均能用于单个IGBT纳秒至微秒级电路仿真。各模型之间的对比如表1所示[29]。

表1 IGBT物理模型建模方法对比
近年来随着建模研究的深入,对于器件组合仿真也有报道。例如,作者团队将改进的Hefner模型以及建立的新集总电荷模型用于器件串并联特性的表征研究,实现了IGBT串并联组合电气特性的准确表征[2,40]。
1.1.2 微秒至十毫秒级瞬态电气建模
针对器件在装置中的瞬态特性仿真,时间尺度按照装置的输出周期,一般为十毫秒级。由于纳秒至微秒级模型复杂,装置级电路仿真效率极低且易发生不收敛问题,因此,需要建立微秒至十毫秒级仿真模型,既能对开关瞬态电压电流尖峰等关键量进行表征,又能满足装置仿真的需求。
根据建模方法的不同,微秒至十毫秒级瞬态建模可归纳为三类。
1)等效电路模型:由电流源、电容、电阻等元器件组成等效电路来模拟IGBT 瞬态行为[41]。也有考虑IGBT基区存储电荷效应的改进等效模型[42],如图8所示,但结构较复杂,对工况的依赖性较大,难以表征温度的影响,适用范围有限。
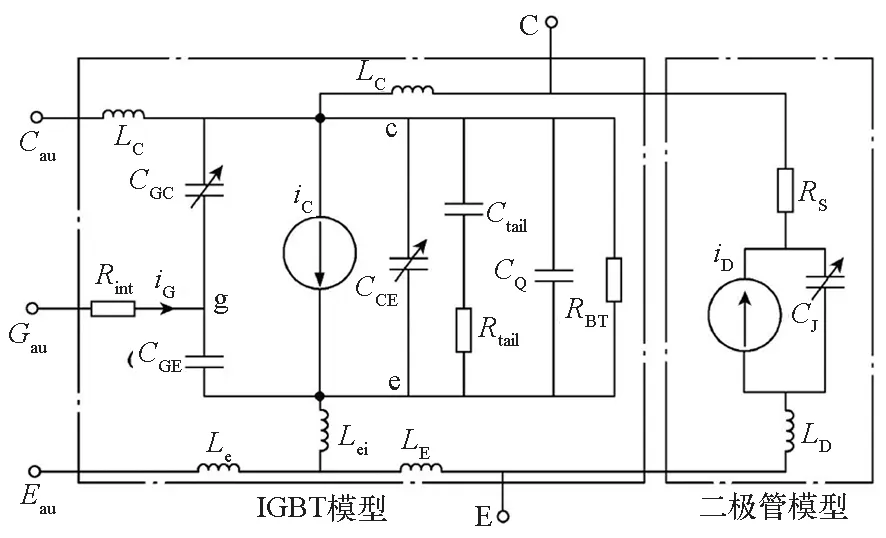
图8 大功率IGBT模块等效电路模型[42]Fig.8 Equivalent circuit model of high power IGBTs[42]
2)拟合模型:将IGBT作为“黑盒”,基于数据拟合来模拟器件开关特性[43]。近年来,有学者采用神经网络算法,对开关特性中的延迟时间、上升时间等参数进行预测[44],开关特性BP神经网络模型如图9所示,但该方法需要大量测试数据,适用工况有限。
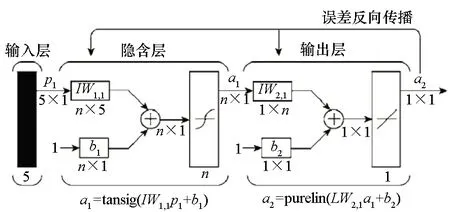
图9 开关特性BP神经网络模型[44]Fig.9 BP neural network of switching transient[44]
3)分段模型:根据物理机理对开关瞬态进行分段,采用线性或低阶拟合相结合,模拟瞬态过程[45-46]。由于拟合系数依赖于工况,该方法适用范围有限。为此,作者团队也提出了一种基于物理模型的分段简化建模方法[7, 47],如图10所示。
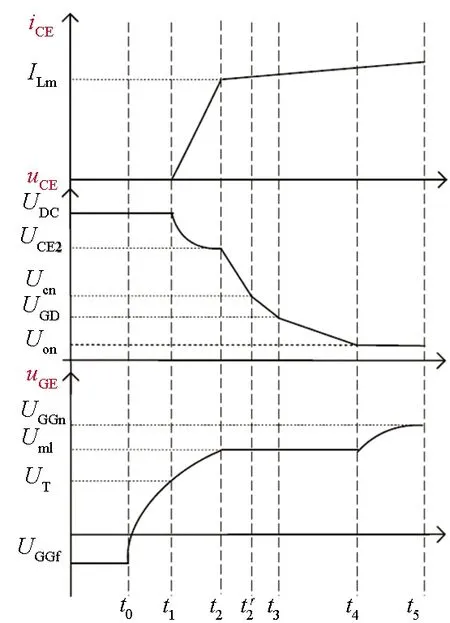
(a) 开通瞬态分段(a) Piece wise of turn-on
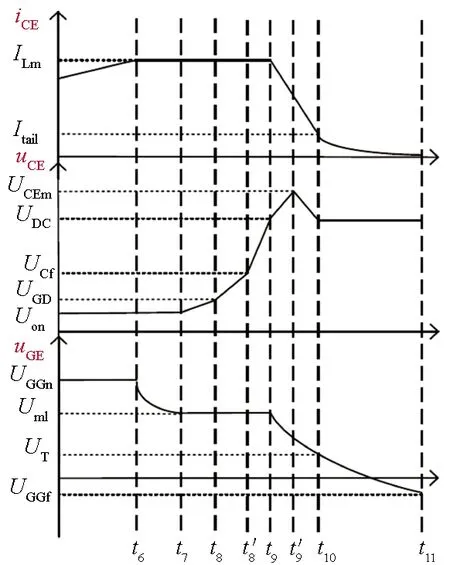
(b) 关断瞬态分段(b) Piece wise of turn-off图10 IGBT开通和关断瞬态分段示意图Fig.10 Piece wise scheme of turn on and turn off transient
由于关键瞬态过程参数例如电流比例系数β采用了物理模型表征,如式(9)~(12)所示,因此该方法可表征不同工况尤其是温度的影响,在仿真精度和仿真效率间取得了较好的折中。简化模型在逆变装置的输出电流、电压仿真波形如图11所示。
(9)
(10)
ICE=In+IP
(11)
β=Imos/ICE
(12)
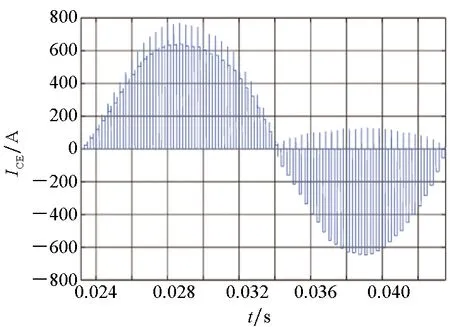
(a) IGBT电流波形(a) ICE waveform of IGBT
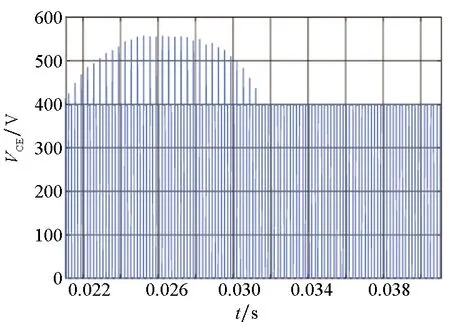
(b) IGBT电压波形(b) VCE waveform of IGBT图11 简化模型在逆变装置的输出电流、电压仿真波形[7]Fig.11 Simulation waveforms of output current and voltage of the simplified model in an inverter[7]
针对十毫秒级以上时间尺度的仿真模型,可以在十毫秒级模型的基础上,进一步作线性简化,提高仿真效率,其原理和十毫秒级模型相同,如图12所示[7]。因此,不再赘述。

图12 分段模型的进一步简化Fig.12 Further simplification of the piece wise model
1.2 IGBT多时间尺度传热建模方法
热特性是影响电力电子器件运行特性的重要因素,也是表征电力电子器件健康状态的重要参量。因此,多时间尺度传热建模是实现器件特性准确表征以及可靠性评估的重要支撑。
文献[48]根据应用对象的不同,将IGBT传热模型分为电路、系统和环境三个尺度。作者团队根据能量传输和热网络结构特点,建立了IGBT多时间尺度结温预测模型,包括短时瞬态微秒级、非稳态毫秒级以及稳态秒级时间尺度[10]。
1.2.1 短时瞬态微秒级结温预测模型
该时间尺度结温预测模型,针对的是短时能量作用,热量几乎全部作用于芯片。其判断标准为热量产生时间小于IGBT芯片与其相邻层热传递的延迟时间,因此一般为微秒级,结温计算如式(13)所示。
(13)
作者团队基于器件物理模型计算的损耗和吸放热模型计算的结温之间的传递,实现瞬态电热耦合仿真,如图13所示,可对IGBT短时脉冲或短路工况下的结温进行准确表征[10]。

图13 微秒级结温预测模型Fig.13 μs-level junction temperature prediction model
1.2.2 非稳态毫秒级结温预测模型
该时间尺度结温预测模型针对的是产热与散热未达到平衡的非稳态,介于短时瞬态和稳态之间,为毫秒级。该时间尺度的传热模型基于IGBT7层封装结构各层间的传热时间常数之间的关系,进行了降阶,如图14所示[48]。
基于开关能量随电压电流的变化规律,建立毫秒级时间尺度下的器件等效损耗与电压电流的关系;基于毫秒级传热模型,建立适用于非稳态毫秒级结温预测模型,如图15所示[10]。该模型主要用于电力电子装置非稳态脉冲序列工作模式下的器件结温表征。

图14 适用于毫秒级热仿真的IGBT传热模型Fig.14 IGBT heat transfer model using in ms-level thermal simulation
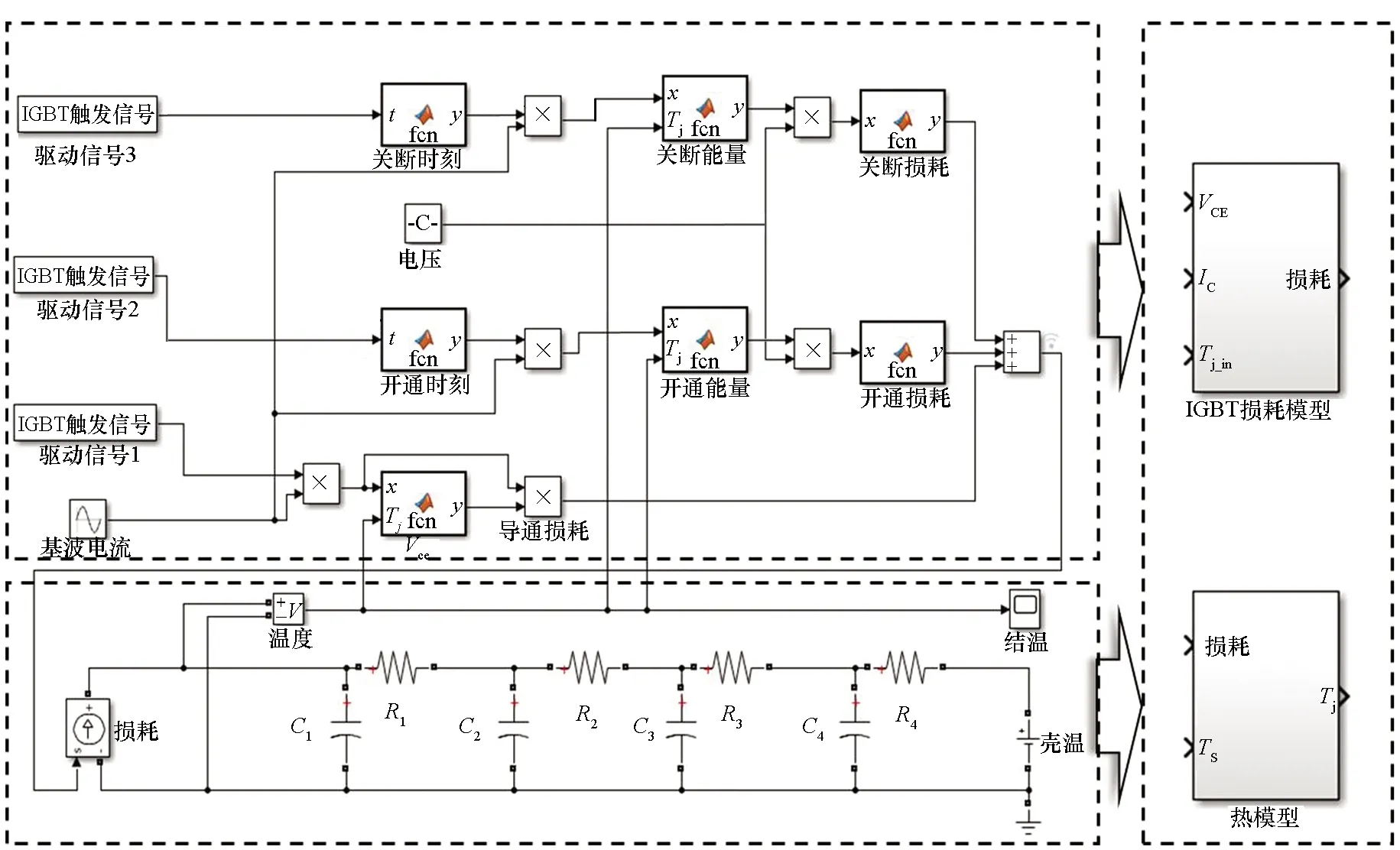
图15 毫秒级结温预测模型Fig.15 ms-level junction temperature prediction model
1.2.3 稳态秒级结温预测模型
适用于秒级热仿真的IGBT结温预测模型,针对的是产热与散热达到平衡的热传递稳态,由传热网络结构各层的时间常数决定为秒级。该时间尺度的传热模型基于毫秒级传热模型进行了进一步降阶,如图16所示[48]。
将IGBT开关周期毫秒级时间尺度内的损耗等效到输出周期内,得到秒级时间尺度下的损耗模型。进而,结合秒级传热模型,建立了秒级结温预测模型,如图17所示。该模型主要用于电力电子装置的稳态工频周期工作模式下的器件结温表征。
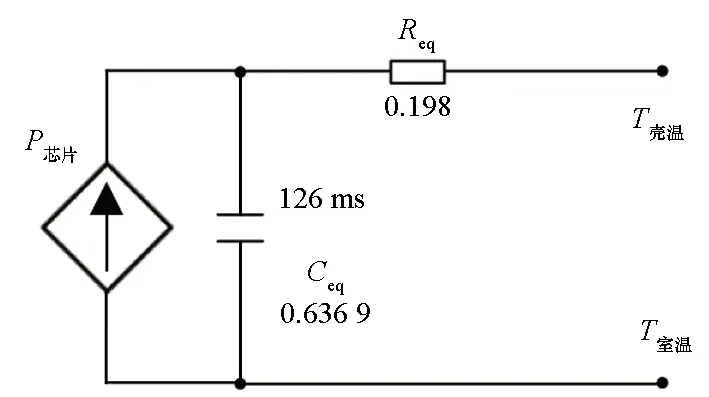
图16 适用于秒级热仿真的IGBT传热模型Fig.16 IGBT heat transfer model using in s-level thermal simulation

图17 秒级结温预测模型Fig.17 s-level junction temperature prediction model
综上,IGBT多时间尺度结温预测模型与传统模型对比如表2所示。在取得较高结温预测精度(5%)的前提下[10],多时间尺度模型实现了仿真效率的大幅提升。
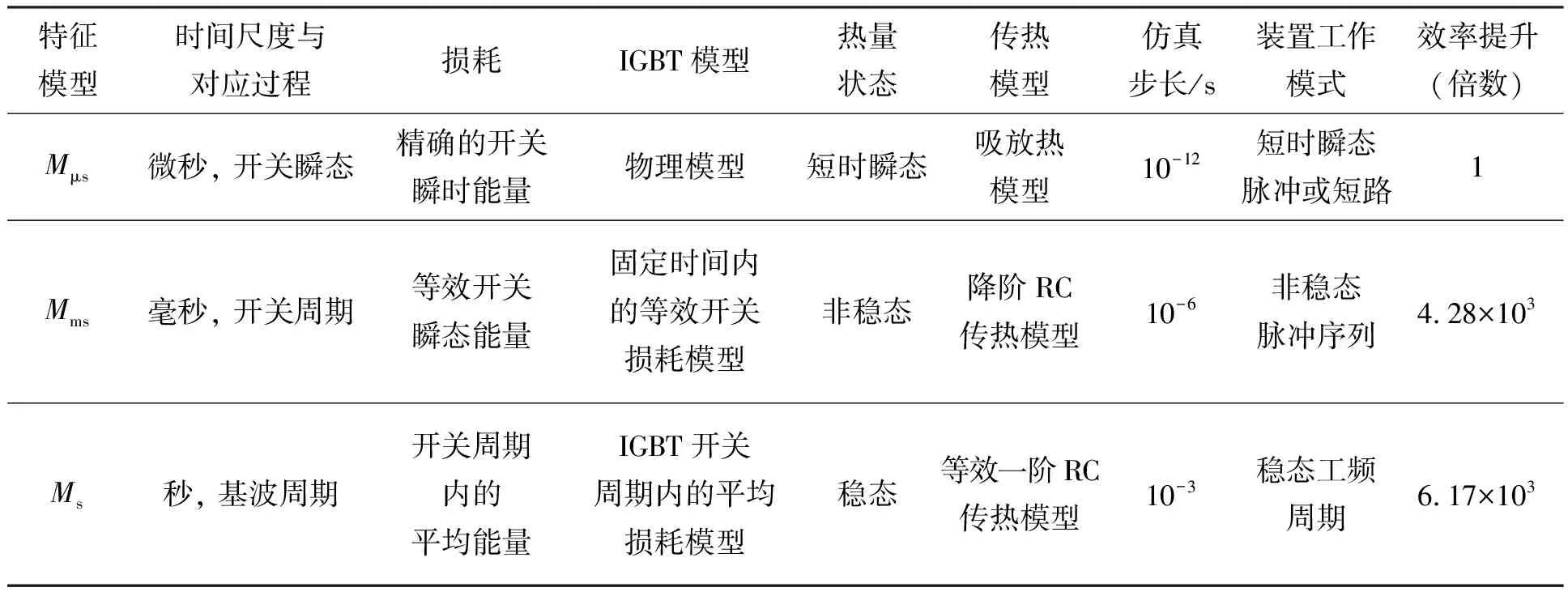
表2 IGBT多时间尺度结温预测模型对比
2 大功率IGBT模块失效量化表征方法
现有器件失效评估方法主要包括定性、半定量和定量的方法[49]。多时间尺度建模的另一个重要目的是为器件的失效量化评估提供支撑。针对器件失效的三个阶段——缺陷、随机、疲劳失效,缺陷失效主要与器件的制备材料和工艺有关,因此基于模型的器件失效量化表征主要针对随机(瞬态)失效和疲劳失效。
2.1 瞬态失效表征方法
器件的瞬态失效主要分为电击穿失效和热击穿失效[49]。前者主要与雪崩击穿相关,包括静态和动态雪崩;后者主要与结温相关,涉及损耗和传热之间的关系。而这些特性的表征均与器件的多时间尺度模型有着重要的联系。
2.1.1 电击穿失效量化表征
IGBT电击穿多发生在器件的关断瞬态,由于电路杂散电感的存在,关断时IGBT集射极会产生电压尖峰,一旦超过器件的击穿电压耐量,将发生雪崩击穿。因此,电击穿量化表征的核心是雪崩击穿电压的表征。

(a) 击穿瞬间(a) Breakdown transient (b) 击穿部位(b) Breakdown location图18 小电流关断电压击穿现象Fig.18 Voltage breakdown at turn off under small current
1)静态雪崩击穿量化表征。IGBT小电流关断时,耐压接近静态雪崩击穿电压。IGBT芯片的平面结横向拓展会在边缘终端处形成柱面结、球面结,使结面曲率减小,电场集中明显,芯片边缘处耐压较中心处大幅降低,在过压关断时率先发生电压击穿[49],如图18所示。对于静态雪崩击穿电压的表征,一种是根据单次雪崩冲击实验求解器件的雪崩耐量来确定击穿电压边界[50];一种是根据元胞结构和掺杂浓度推导击穿电压,如式(14)所示FS型IGBT静态击穿电压[14];还有一种是采用TCAD设计软件对不同终端结构下的击穿电压进行仿真分析[51]。
(14)
2)动态雪崩击穿量化表征。在IGBT硬关断过程,由于电流较大,发射极侧的最大电场受到局部电荷密度的强烈影响,达到碰撞电离的临界值,这种现象即为动态雪崩现象。动态雪崩发生时,集射极电压虽未达到稳态击穿电压,但会使电流下降速率、电压上升速率减小,关断损耗增加。动态雪崩发生后导致局部产生高电流密度的电流丝,引起IGBT失效[52-53],如图19所示。

图19 IGBT大电流关断动态雪崩击穿现象Fig.19 Dynamic avalanche breakdown phenomenon of IGBT turn off under large current
对于动态雪崩击穿的量化评估,目前主要是基于TCAD软件仿真,判断是否达到结温安全边界[54]。由于电流丝是跳动的,该方法难以考虑芯片表面电流密度分布对动态雪崩电学特性的耦合影响,如图20所示;通过工艺仿真确定共集电极放大系数对动态雪崩载流子抽取的影响,但对击穿过程还没有具体的量化表征[55];研究长期处于动态雪崩的IGBT关断电流变化规律,但没有给出器件失效边界的量化表征方法[56]。作者团队也对动态雪崩击穿的建模进行了研究,在器件物理模型基础上,基于雪崩倍增因子对模型边界条件、载流子分布的影响,获得动态雪崩的模型表征,关键电流如式(15)~(16)所示,仿真结果如图21所示。
(15)
(16)

(a) t1=60.20 μs (b) t2=60.27 μs图20 动态雪崩关断电流丝跳动情况[54]Fig.20 Dynamic current filaments at dynamic avalanche[54]

(a) 动态雪崩击穿仿真波形(a) Simulation waveforms of dynamic avalanche
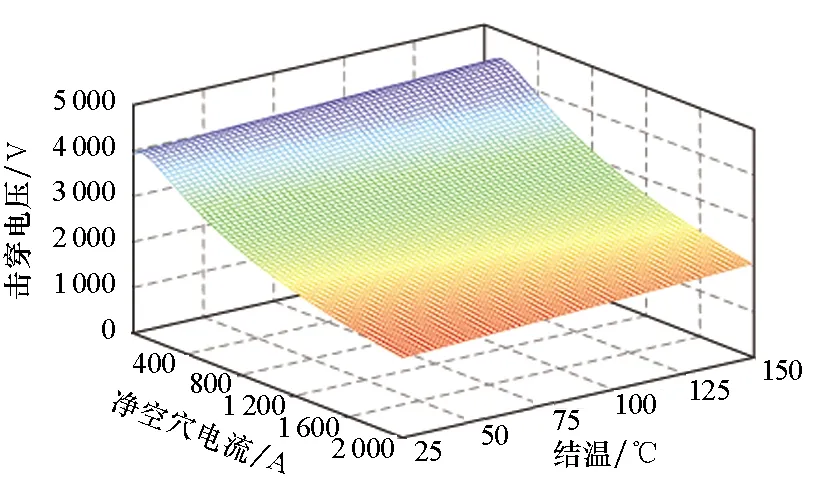
(b) 击穿电压与净空穴电流和结温的关系(b) Relationship among breakdown voltage, net hole current and knot temperature图21 动态雪崩击穿仿真波形及击穿电压变化规律Fig.21 Simulation waveforms of dynamic avalanche model and its variation rule
2.1.2 热击穿失效量化表征
功率器件无论在导通稳态、开关瞬态还是截止状态都存在功率损耗。针对单次瞬态大电流脉冲,有源区产生的热量全部耗散在芯片,产生温升;而对于连续周期脉冲,需要考虑温度累积效应。材料温升达到热极限,器件将发生热击穿,表现为芯片大面积烧蚀,严重情况伴随键合点的脱落或熔断,如图22所示。

图22 IGBT热击穿现象Fig.22 Thermal breakdown of IGBTs
IGBT热击穿量化表征方法主要有两类:第一类是基于损耗和数据手册提供的热阻抗曲线计算结温,该方法未考虑温度累积效应,难以从设计角度预测热击穿发生的边界[57-58]。第二类是基于热平衡的方法[15],即通过判断器件的产热与散热曲线之间的相对关系,确定器件热击穿的安全边界,如图23所示。图24则是基于IGBT多时间尺度模型对极端条件下的电热特性的仿真,实现其热击穿失效的量化评估。
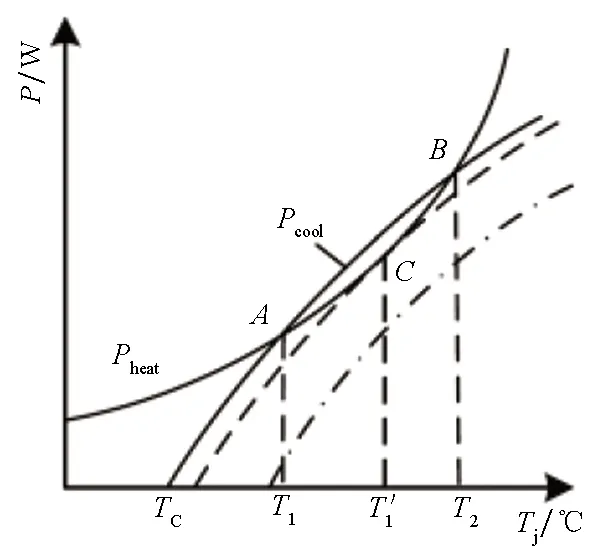
(a) IGBT热平衡分析示意图(a) Diagram of thermal equilibrium analysis

(b) 基于热平衡的IGBT热击穿量化评估流程(b) Thermal breakdown evaluation progress based on thermal equilibrium图23 基于热平衡分析的IGBT热击穿量化评估方法[15]Fig.23 Thermal breakdown evaluation method based on thermal equilibrium analysis[15]

(a) 电路原理图(a) Circuit scheme

(b) 短路电流波形(b) Short-circuit current waveform

(c) 端子1短路温升波形(c) Temperature rise of node 1图24 IGBT模块内部3个并联功率单元 电流等效电路及结果对比Fig.24 Simulation and testing results of equivalent circuit of the three parallel power units in the IGBT module
2.2 疲劳失效表征方法
在疲劳失效表征方面,现有研究主要集中在对引起失效的各种外部因素的分析上,通过端口量的变化来反映疲劳程度[49,59-60]。
作者团队对IGBT芯片与封装疲劳失效机理进行了长期的研究,在查明失效特征量随疲劳老化演变规律的基础之上,建立了IGBT疲劳失效的量化表征方法。
2.2.1 芯片疲劳失效表征
目前研究发现,芯片疲劳的表征量主要有阈值电压、漏电流和关断时间等。
1)基于阈值电压的IGBT疲劳表征[59]。当IGBT发生疲劳后,栅极界面电荷密度δQss发生变化 ,包括可动离子电荷δQm、界面陷阱电荷δQit和氧化层陷阱电荷δQot,如式(17)所示。通过式(18)可知,δQss变化引起IGBT阈值电压发生变化,通过阈值电压偏离正常值的程度,即可判断IGBT疲劳程度。
δQss=δQm+δQit+δQot
(17)
(18)
综合阈值电压疲劳特性推导过程,建立IGBT阈值电压疲劳表征模型,如图25所示,可以计算不同寿命阶段IGBT器件的阈值电压。图26为阈值电压随应力施加时间的变化规律,其仿真结果表明,随着应力施加时间的不断累积,阈值电压逐渐增大,呈现先快后缓的趋势。
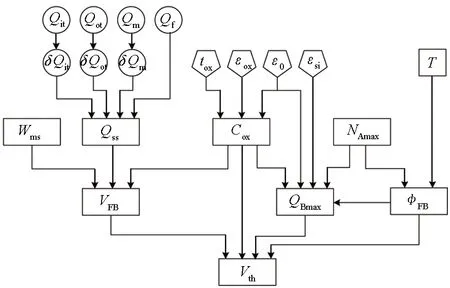
图25 阈值电压疲劳状态表征模型Fig.25 Threshold voltage fatigue model
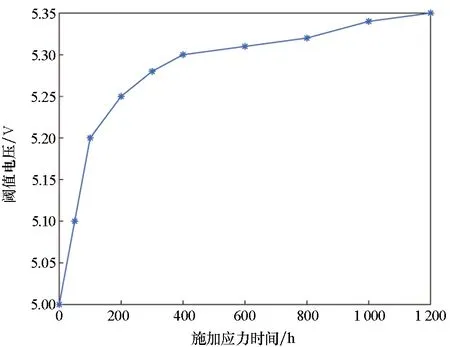
图26 阈值电压随应力施加时间的变化规律Fig.26 Variation of threshold voltage with fatigue time
2)基于集射极漏电流的IGBT疲劳表征[60]。当栅极电压小于平带电压时,IGBT产生疲劳后,发射极界面产生漏电流,随着疲劳程度的加剧,漏电流逐渐增大。当栅极电压大于平带电压而小于阈值电压时,硅材料发生疲劳后,栅极界面状态发生变化,沟道电流随疲劳程度的增大逐渐增大。同时发射极界面漏电流也会增大。因此,可分别建立针对不同阶段的漏电流疲劳状态表征模型,如式(19)所示。不同集射极电压下集射极漏电流随疲劳时间的变化规律如图27所示,近似呈线性增大规律。
(19)
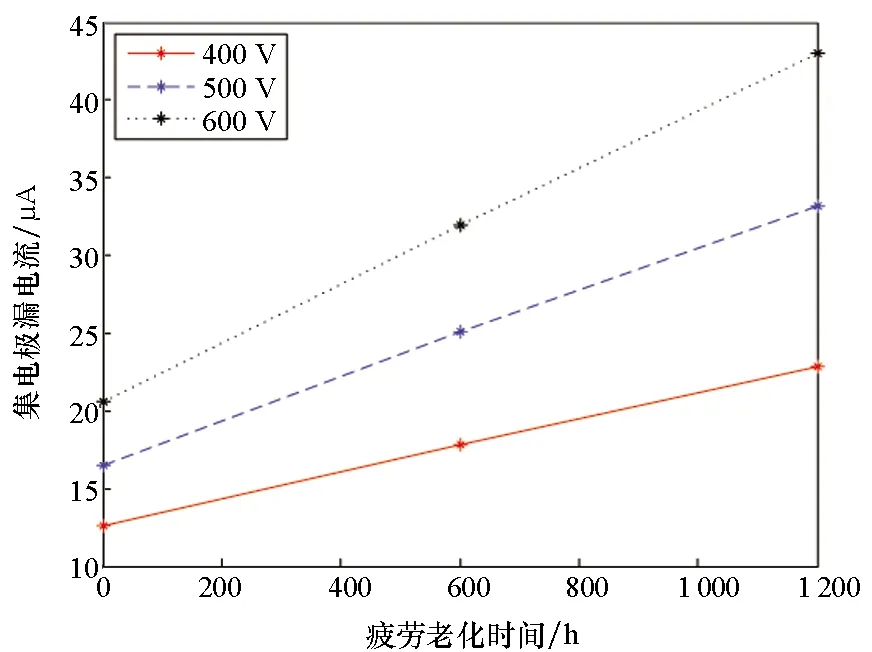
图27 不同集射极电压下,IGBT集射极 漏电流随疲劳时间的变化规律Fig.27 Variation of colleter emitter current with fatigue under different collector emitter voltage
3)基于关断时间的IGBT疲劳状态表征。疲劳后阈值电压增大会影响关断时间。因此通过关断时间也可以表征器件的疲劳状态。IGBT关断时间的定义如下,关断时间随疲劳呈线性关系增大,如图28所示。
toff=td(off)+Δt+tf
(20)
(21)
(22)
2.2.2 封装疲劳失效表征
目前,对IGBT封装疲劳失效研究的报道较多,主要集中在键丝疲劳和焊料层疲劳失效,本质上是电-热-机械应力的作用。基于封装疲劳失效机理的研究结论,表征疲劳程度的特征量主要有热阻和集射极饱和压降等[49]。

(a) ICE=0.6 A
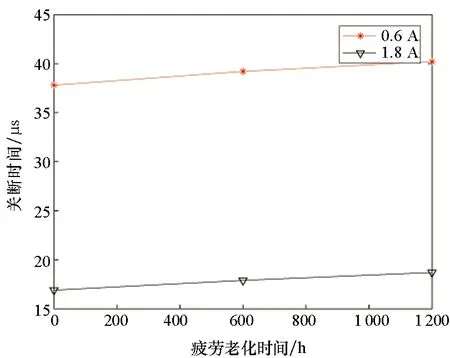
(b) UCE=900 V图28 不同电压、电流下关断时间随 疲劳时间的变化规律Fig.28 Variation of turn off time with fatigue time under different voltage and current
1)基于热阻的IGBT疲劳表征。焊料层疲劳主要表现为空洞的产生和扩展,而空洞率是衡量焊料层空洞水平的重要指标,空洞率增大导致器件传热路径热阻增大。因此,现有研究建立了IGBT焊料层空洞随疲劳的变化规律,进一步得到结壳热阻随焊料层疲劳的变化规律,如图29所示[61]。因此,通过热阻的变化可以表征器件的封装疲劳程度。

图29 不同结温波动下模块结壳热阻 随功率循环次数的变化曲线Fig.29 Variation of junction-to-case thermal resistance with power cycles under different temperature swings
2)基于集射极饱和压降的IGBT疲劳表征。模块的键丝疲劳会产生裂纹、断裂以及焊盘剥离,导致封装等效电阻增大,饱和压降增大。因此,基于饱和压降的变化,可对IGBT模块的键丝疲劳状态进行评估。作者团队通过研究IGBT模块集射极饱和压降5个组成部分随模块疲劳老化进程的变化规律,得出键丝和焊点的压降变化为IGBT疲劳压降变化的主要原因,如图30所示。基于功率循环实验得到饱和压降随疲劳的变化规律,表现为先缓变后陡变,如图31所示。

图30 IGBT模块各部分压降变化量占初始值的百分比Fig.30 Ratio of voltage change to the initial value of each part of IGBTs

图31 IGBT模块饱和压降随功率循环次数的变化规律Fig.31 Variation of saturation voltage with power cycles
3 IGBT组合多速率仿真方法
目前针对功率半导体器件及其组合特性的表征需求,可将其分为路-路耦合[19-20]、场-场耦合[21-23]以及场-路耦合[24]三种仿真方法。从仿真精度、仿真效率以及信息表征全面性三个方面对三种仿真方法进行对比,如表3所示,场路耦合的仿真方法更具应用前景。

表3 IGBT电热耦合仿真方法对比
场-路耦合仿真构架主要包括三部分[25-26]:电路模型(Simulink)、有限元场模型(COMSOL)以及脚本控制(MATLAB),如图32所示,通过温度与损耗的相互传递,实现场-路双向耦合。
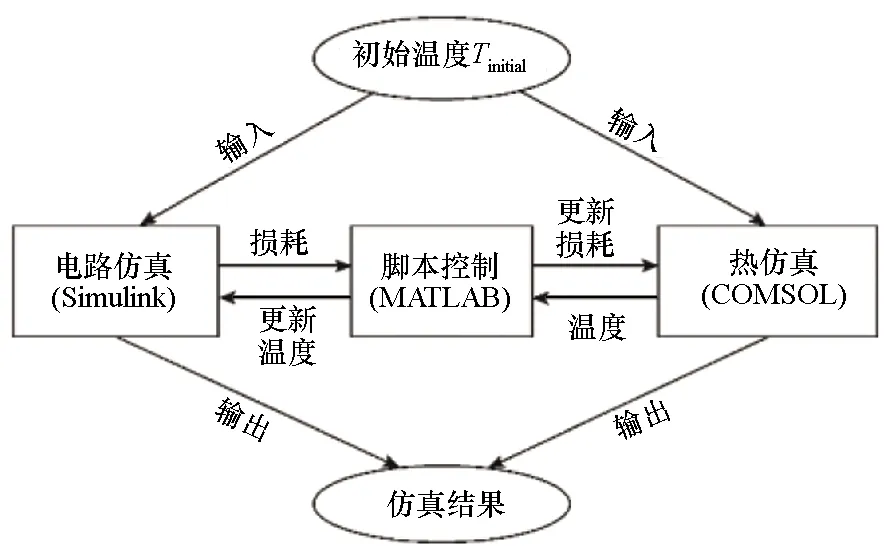
图32 场-路耦合仿真原理Fig.32 Scheme of field-circuit coupling simulation
由于场-路耦合仿真中的电路模型和热场模型存在明显的时间尺度差异,因此采用多速率仿真策略也是场-路耦合仿真的必然要求。由图32可知,通过灵活调节电路仿真步长、场仿真步长以及场-路之间的数据交换步长,可在满足仿真精度的基础上尽可能提高仿真效率。
作者团队采用多速率仿真方法有效解决了IGBT多物理场仿真中的多时间尺度协调问题:电路仿真步长纳秒或皮秒级;热场仿真步长微秒或毫秒级;然后调节场-路数据交换步长控制仿真效率。以短路和浪涌工况为例实现了器件电气、热场以及应力特性准确表征,如图33~35所示[25-26],仿真效率较单一时间尺度提升两位数。

图33 多速率联合仿真的步长控制方法Fig.33 Step control of the multi-rate simulation

(a) 电气特性(a) Electrical characteristic

(b) 热分布特性(b) Thermal distribution characteristic
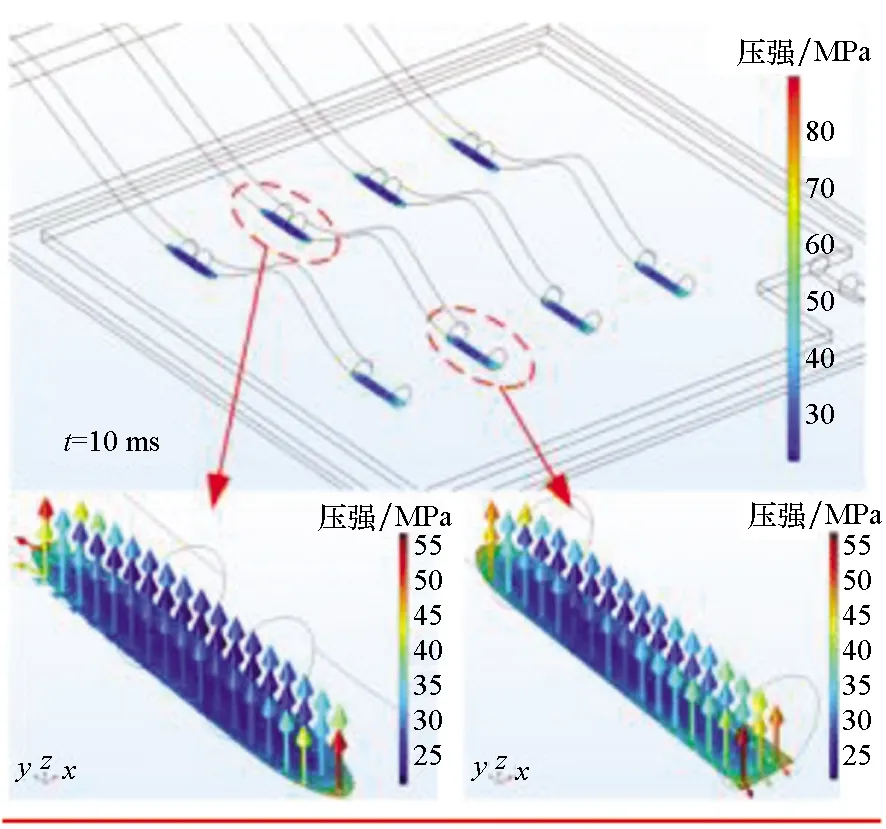
(c) 应力分布(c) Stress distribution图34 多速率仿真在IGBT短路仿真中的应用Fig.34 Multi-rate simulation in IGBT short-circuit simulation
4 器件多时间尺度模型在装置设计中的应用
4.1 电气边界的安全设计
以二极管物理模型在整流装置中的优化设计为例进行说明。
PIN二极管反向恢复瞬态,由于电路杂散电感以及变压器漏感的存在,易产生电压尖峰,影响器件及装置的安全运行,因此需要吸收电路。目前,吸收电路设计一般是试错或将二极管结电容等效为定电容的方法,工作量大且精度不高。作者团队利用建立的二极管物理模型,提出了基于器件组合仿真的二极管反向恢复尖峰电压RC吸收电路最优参数设计方法[5, 62]。

(a) 电气特性(a) Electrical characteristics

(b) 热分布特性(b) Thermal distribution charateristic图35 多速率仿真在SiC二极管组合浪涌仿真下的应用Fig.35 Multi-rate simulation in SiC diode surge

图36 二极管及吸收电路组合等效仿真电路Fig.36 Equivalent circuit of diode and snubber circuit
将整流二极管模型代入图36所示的组合电路中进行仿真,得到二极管反向恢复电压尖峰随吸收电阻RS和吸收电容CS的变化规律,如图37所示[62],同时,还要满足RS的损耗要求,得到吸收电路的最优参数。二极管开关瞬态电压尖峰仿真与实验对比情况如图38所示,优化前,母线电压为1 500 V时,二极管反向恢复尖峰电压已达到2 073 V,若工作在母线电压为3 000 V以下,则尖峰电压将接近器件4 500 V耐压值;优化后,母线电压为3 000 V时,二极管反向恢复尖峰电压降为约2 500 V,满足器件的安全运行电压范围,实现了电气安全边界的准确评估。

图37 二极管电压尖峰随吸收参数变化图Fig.37 Voltage peak variation of diode with snubber parameters
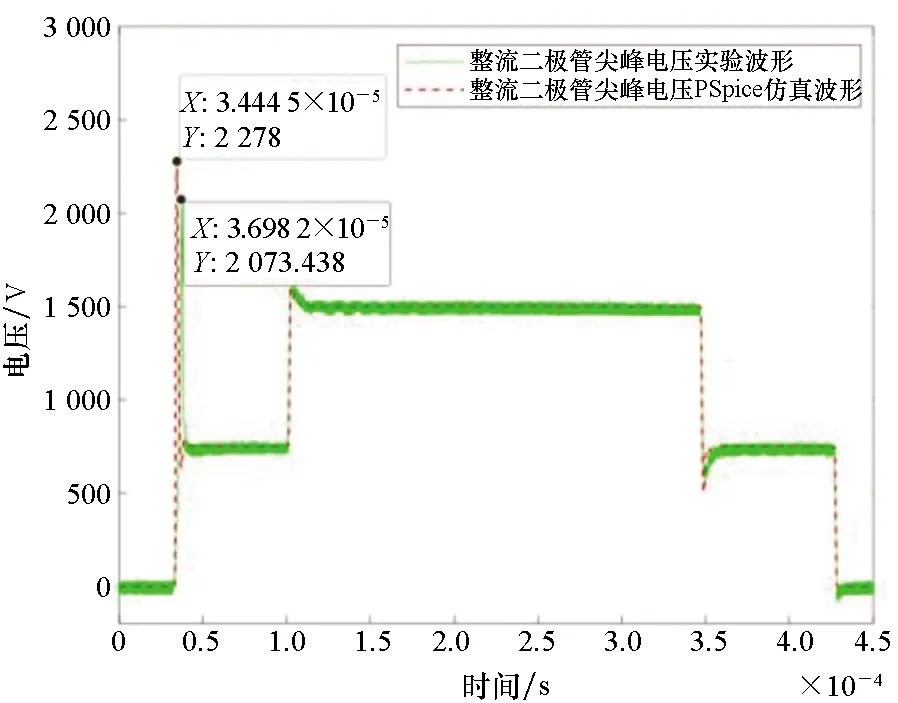
(a) 优化前:RS=100 Ω,CS=30 nF(a) Before optimization: RS=100 Ω,CS=30 nF
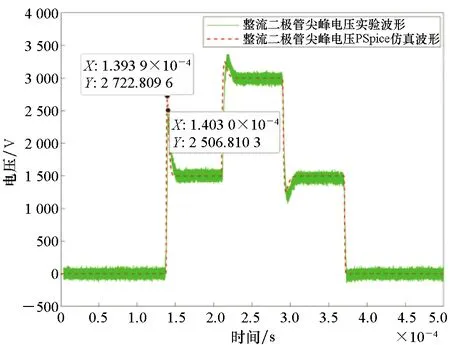
(b) 优化后:RS=39 Ω,CS=110 nF(b) After optimization: RS=39 Ω,CS=110 nF图38 二极管开关瞬态电压尖峰仿真与实验对比Fig.38 Simulation and testing results of transient voltage peak of diode
4.2 基于结温的优化设计
IGBT器件的损耗是导致结温升高的重要因素,它与母线电压、调制比、驱动电阻、开关频率、基波频率、功率因数等均相关。作者团队基于模块结温与系统参数之间的互动关系,结合多时间尺度结温预测模型,提出了一种基于结温的电力电子器件及系统多目标优化设计方法。
以某型推进变频器为例,IGBT开关频率较高(4 kHz),开关周期内的结温波动较小,所以采用秒级结温预测模型对可行方案进行仿真分析,如表4所示。在保证均流特性的前提下,减小驱动电阻,是降低器件结温、提高装置效率的有效途径。优化后方案3较方案1的器件最高结温和结温波动均有大幅降低,如图39所示。

表4 某型推进变频器结温优化参数设计方案

(a) 优化前:Rgon=3 Ω,Rgoff=3.5 Ω(a) Before optimization:Rgon=3 Ω,Rgoff=3.5 Ω
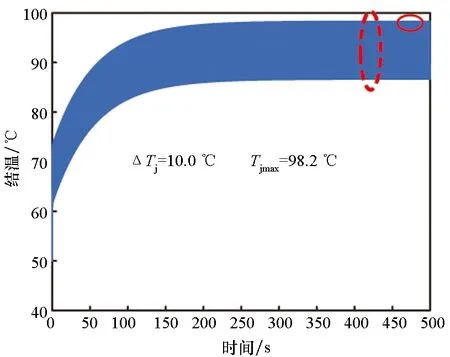
(b) 优化后:Rgon=2 Ω,Rgoff=3 Ω(b) After optimization:Rgon=2 Ω,Rgoff=3 Ω图39 驱动电阻优化前后IGBT结温运行规律Fig.39 IGBT junction temperature at different driver resistors
该方法也在移动变频器上进行了应用,效果如图40所示。优化后的IGBT最高结温和结温波动均得到了较大幅度的减小。
总体来说,优化后的IGBT器件最高结温和结温波动分别减小约30%和41%,对器件的可靠性和寿命提升有重要帮助。
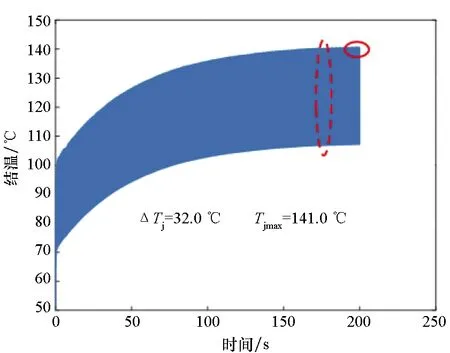
(a) 优化前(a) Before optimization
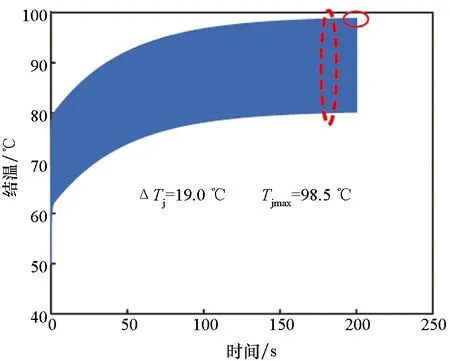
(b) 优化后(b) After optimization图40 某移动变频器上的IGBT结温优化效果Fig.40 IGBT junction temperature of a mobile converter
5 结论
电力电子器件及其组合多时间尺度动力学表征方法,为解决现代大容量电力电子混杂系统多时间尺度的精确设计难题,提供了关键的器件层面的支撑,有助于提升我国大容量电能变换装置的整体设计水平:
1)多时间尺度电热瞬态建模实现了器件从纳秒至秒级的电热特性准确表征,为器件可靠性以及装置精确设计提供模型基础。
2)基于器件多时间尺度模型,可以实现器件失效分析从定性和半定量向定量的提升,提升器件及装置的可靠性分析水平。
3)多速率仿真方法,可有效解决器件组合多时间尺度特性的仿真问题,为器件和装置的精确设计提供重要的仿真手段。
总的来说,电力电子器件多时间尺度动力学表征是当前电力电子领域的重要研究热点之一,取得了一定成果。后续结合新材料功率半导体器件,在复杂多场耦合与驱动控制的关系、多时空尺度建模以及极端工况下器件的可靠性评估等方面,值得继续深入研究。
