裂纹叶片非线性振动响应理论分析与实验验证*

沈国际，官凤娇，边子方，胡海峰，杨拥民

(1. 国防科技大学 智能科学学院， 湖南 长沙 410073； 2. 国防科技大学 装备综合保障技术重点实验室， 湖南 长沙 410073)

疲劳裂纹严重威胁发动机的使用安全，引发了包括2018年美国西南航空发动机爆炸在内的多起飞行事故，因此叶片早期裂纹检测和损伤评估对于航空安全和航空发动机发展具有重要意义。相比于应变片监测和人工表面检测，振动信号分析方法有望实现叶片裂纹的在线监测，因此得到了广泛重视[1-4]。根据所用裂纹模型，叶片振动信号分析方法可以分为三类：基于开裂纹模型的方法，基于双线性裂纹模型的方法，基于呼吸裂纹模型的方法。

开裂纹模型最早得到发展，借助开裂纹模型，可以解析确定裂纹叶片固有频率与裂纹尺寸的定量关系。Gudmundson[5]较早研究了开裂纹叶片的动力学模型，推导了正常叶片和裂纹叶片的固有频率表达式。Shen和Pierre[6]分析了对称开裂纹梁的运动规律，重点研究了裂纹尖端附近的应力集中情况，分析了叶片振动的模态和固有频率。Shen和Pierre[7]还研究了Bernoulli-Euler梁的边界条件，引入了一个裂纹度量函数来描述裂纹应力集中现象。Owolabi等[8]测量了不同裂纹位置和裂纹深度时含裂纹梁的固有频率和相应振幅。Law和Lu[9]利用Dirac函数对包含开裂纹的梁进行了建模，并研究了包含单个裂纹梁的时域响应，这表明振动信号分析可用于识别裂纹和评估损伤。

有研究发现，开裂纹模型得到的固有频率与实测固有频率存在较大误差，从而逐渐发展出双线性裂纹模型。这种模型认为在压力载荷作用下，裂纹并不总是张开的，而是在张开和闭合状态间进行周期性转换，相应地，叶片刚度在两个特征刚度之间进行周期性切换[10]。Chatterjee[11]用多项式方法研究了具有双线性刚度的单自由度系统，得到了含裂纹梁在谐波激励下的响应输出。Andreaus等[12]用无摩擦双线性模型模拟了裂纹动态变化行为，将裂纹引起的响应变化归纳为次谐波和超谐波等现象。

近年来，为了更为精细地表征裂纹动态行为，越来越多的研究集中在呼吸裂纹模型上。在双线性裂纹模型中裂纹在张开和闭合两种状态阶跃性变化的基础上，呼吸裂纹模型认为裂纹张开、闭合是连续变化的过程，裂纹张开程度随着载荷的振荡而变化。基于仿真模拟和实验分析，对含呼吸裂纹的叶片振动响应开展了大量研究。Cheng等[13]等用余弦函数描述裂纹刚度的变化，表明呼吸裂纹模型比开裂纹模型更适合用于早期裂纹检测。Long等[14]通过有限元分析，推导了含呼吸裂纹的非线性动力学模型方程，并利用多尺度法研究了裂纹梁在谐波激励下的稳态响应。Ma等[15]应用平面单元和梁单元相结合的方法，对裂纹梁的振动进行了研究，表明裂纹角度对振动振幅也有显著影响，在某些特定角度裂纹作用下梁的振动幅值更大。Broda等[16]研究了呼吸裂纹梁的纵向振动，特别是裂纹引起的非线性幅值局部变化。Pugno等[17]提出了一种逐步收敛的迭代方法来计算谐波分量的系数。Bovsunovskii和Surace[18]研究了考虑阻尼系数变化的呼吸裂纹效应。这种方法在描述裂纹行为方面更为精细，但是使得含裂纹梁的动力学模型只能用非线性方程来表征，因而难以得到显式解。

综合上述研究成果，尽管裂纹叶片振动信号的特征提取已经取得了一定的进展，但由于呼吸裂纹非线性振动运动方程无法得到响应解的解析表达式，对复杂叶片振动的理论分析仍然是悬而未决的工作。因此，有必要开展叶片裂纹振动的精细化描述，发展新的非线性分析方法，探究裂纹叶片振动的动力学过程演变规律，发展更多振动特征分析方法，通过多特征融合提高裂纹识别的准确性。

本文从呼吸裂纹模型出发，建立裂纹叶片的悬臂梁模型来表征叶片振动，分析裂纹深度和位置对叶片动力学参数的影响规律。通过推导，证明了谐波分量的功率由相邻谐波功率、谐波阶次和裂纹引起的刚度变化等参数决定，并得到了谐波分量相对功率与裂纹参数的定量化描述。在此基础上提出了基于谐波分量相对功率的特征分析方法，并得到了数值仿真和实测叶片数据的验证。

1 叶片振动建模

裂纹叶片可简化为如图1所示的矩形悬臂梁。其中，a为裂纹深度，b为梁厚度，w为叶片宽度，L为梁长度，lc为裂纹距叶尖的距离。

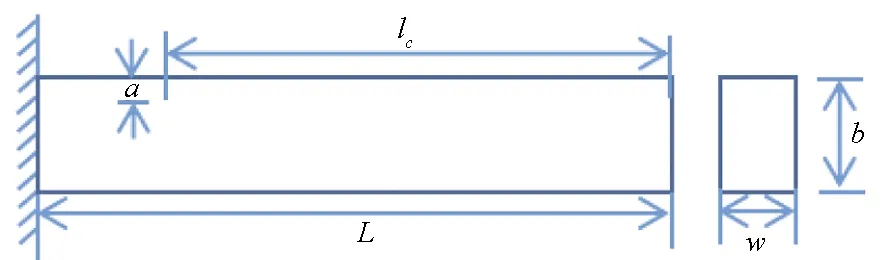
图1 叶片的悬臂梁模型Fig.1 Blade cantilever beam model

矩形悬臂梁的广义柔度f0计算公式如下[17]：

(1)

其中，E为叶片材料对应的杨氏模量，I为矩形梁的转动惯量。

当叶片出现裂纹时，叶片的柔度将相应地变化。对于含开裂纹的梁，其柔度为：

fopen=fΔc+f0

(2)

开裂纹引起的柔度变化已经由Dimarogonas等[19]推导得到：

(3)

其中，ν是叶片材料的泊松比，系数φ定义如下[19]：

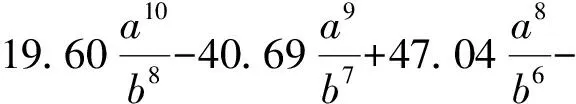
(4)

对于早期裂纹，考虑到裂纹深度远小于叶片厚度，a≪b，因此系数φ可近似估算为：

φ≈0.63a2

(5)

在周期性载荷作用下，裂纹梁的刚度是周期性变化的。当载荷以频率ω1变化时，裂纹也会周期性地张开和闭合，形成所谓的“呼吸裂纹”。此时叶片的时变刚度可近似为[13]：

k(t)=k0+kΔc[1+cos(ω1t)]

=k1+kΔccos(ω1t)

(6)

其中，刚度变化幅值[13]为：

(7)

平均刚度[13]为：

k1=k0+kΔc

(8)

对于早期裂纹，综合式(3)、式(4)、式(7)，可得

(9)

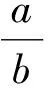
kΔc≪k1

(10)

因此，裂纹梁自由端部振动(即裂纹叶片叶尖振动)u的动力学模型可表示为：

(11)

式中，m为等效质量，c为阻尼系数，F为激振力幅值。

假设u(t) 是方程(11)的解，易证u(t) 是频率ω1的周期函数，因此解u(t)可用傅里叶级数表示如下：

(12)

其中，谐波角频率ωn=nω1,Gn和Kn是傅里叶系数。

u(t)的一阶和二阶导数如下：

(13)

(14)

相应地，式(11)可推导为 ：

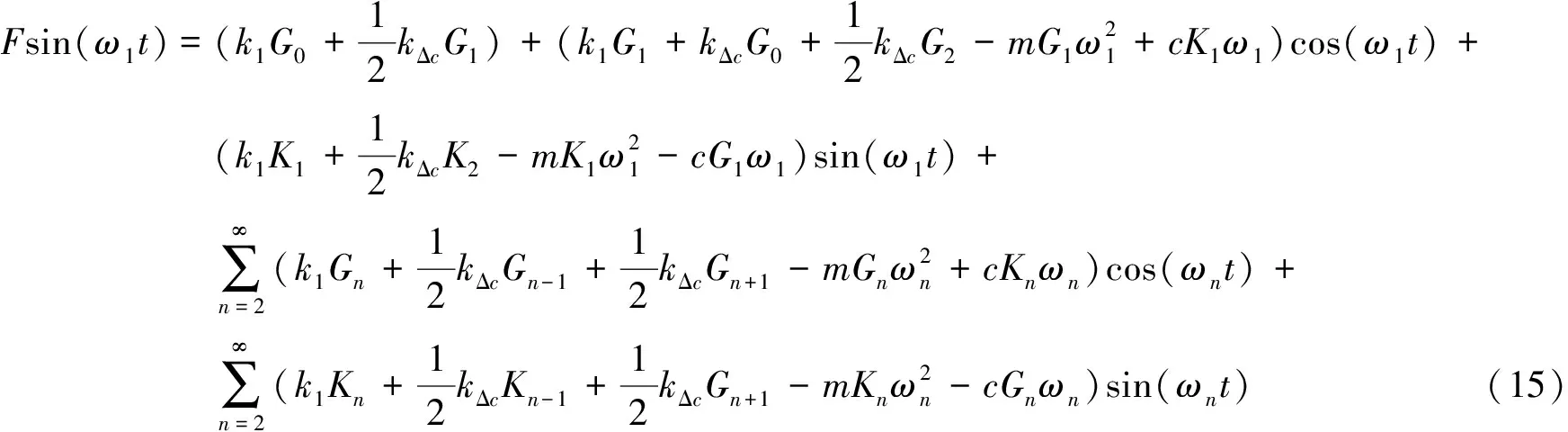
通过平衡n次谐波的系数，可得：

(16)

(17)

其中，n≥2。

进一步由式(16)和式(17)，可得：

(18)

(19)

为了简化推导，将n次谐波分量的功率定义为：

(20)

据此，将式(18)和式(19)分别平方，然后相加，则n次谐波分量的功率为：

(21)

因此，对于任意n≥2，有：

(22)

每个谐波分量的功率相对于相邻低一阶分量的功率可定义为谐波分量相对功率：

(23)

2 数值模拟

为验证上述结论，对含有纵贯裂纹的矩形直板叶片进行数值模拟。

2.1 参数设置

仿真用直板叶片尺寸选择，即长L=0.4 m，宽w=0.1 m，厚度b=0.002 m，裂纹到根部的距离设置为lc=0.9L。阻尼比ξ=0.01，定义为ξ=c/(2mω0)，其中ω0为叶片的一阶固有频率。叶片材料选用不锈钢，杨氏模量为E=2.09×1011N/m2，泊松比v=0.269。采用四阶或五阶RungeKutta方法对动力学方程(11)进行数值求解。考虑到激振力幅值对谐波分量相对功率无显著影响，取激振力幅值F=1 N。

2.2 定性分析

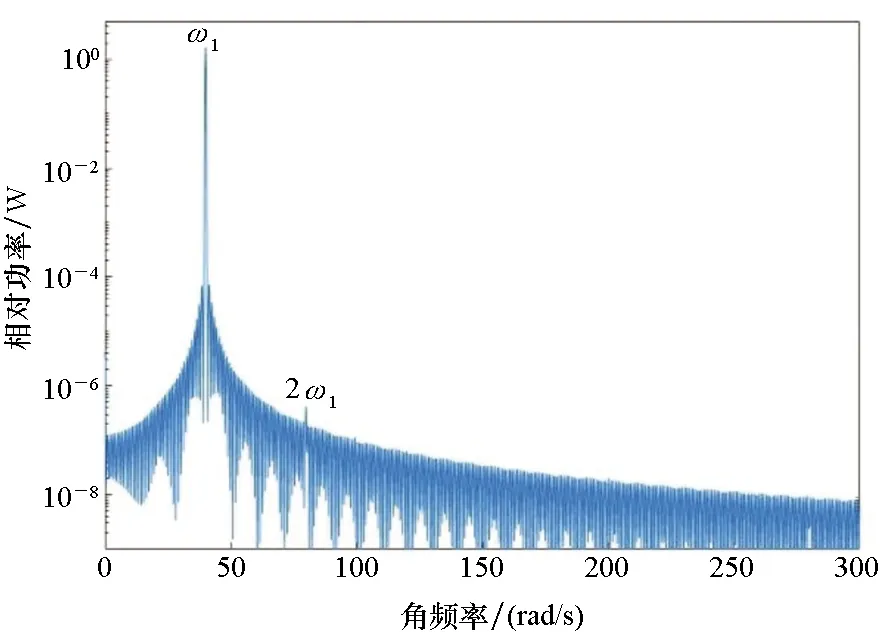
根据上述参数，不锈钢叶片的固有频率为ω0=67.86 rad/s。考虑到叶片工作频率需要远离固有频率，以免引起叶片共振，对10～40 rad/s频段内多个激励频率进行了分析。以激励频率ω1=40 rad/s为例，其动态响应的功率谱如图2所示。

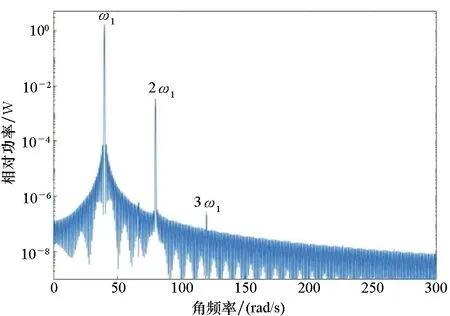
(a) a=0.5b

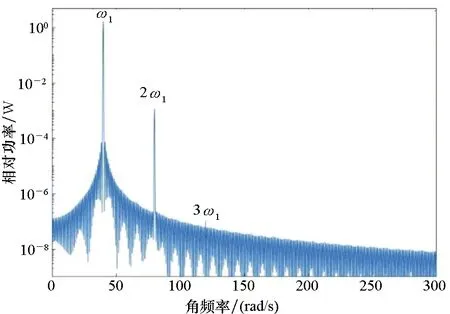
(b) a=0.4b

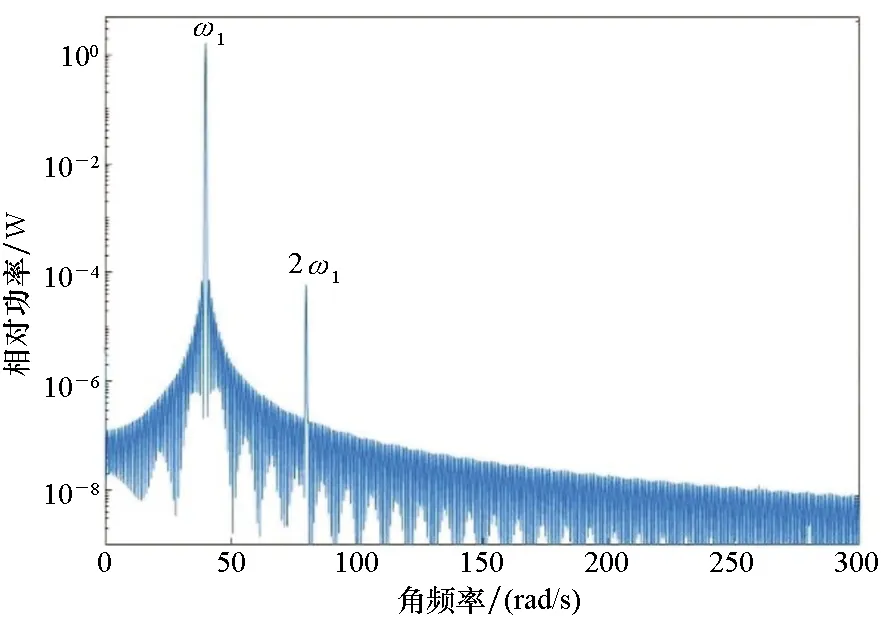
(c) a=0.2b

(d) a=0.05b图2 不同尺度裂纹的叶片功率谱Fig.2 Spectrum of blade vibration for different crack size

从图2中可以看出，振动频谱由少数谐波成分主导，而且这些谐波分量的功率随谐波阶次的增加而衰减，低阶分量的功率远大于相邻高阶分量的功率。在图2(a)中，容易地分辨出前三次谐波分量。图2(b)～(d)中，一次谐波分量几乎没有变化，但是高次谐波分量的峰值随着裂纹相对深度的减小逐渐减少。

2.3 定量分析

对比图2所示的各次谐波功率谱值，可以看出，对于深度较大的裂纹，相同阶次谐波分量的功率幅值更大。虽然一次谐波分量的功率在所分析的情况下几乎相同，但二次谐波分量的功率从图2(a)中裂纹深度为a=0.5b时的3.8×10-3W，减少到图2(d)中裂纹深度为a=0.05b时的 4.2×10-7W。

图2清楚表明，在大多数情况下，随着谐波次数的增加，谐波功率快速衰减，二次谐波相对功率比更高次谐波相对更为明显，容易得到分辨。因此，采用二次谐波相对功率作为特征参数，有利于减少随机噪声影响，提高诊断准确率和鲁棒性。

在其他激励频率(叶片载荷变化频率)作用下，仿真分析可以得到类似结论。

3 裂纹检测应用

3.1 裂纹识别方法

对于正常叶片，叶片运动接近理想设计状态，非线性效应可以忽略不计，即式(11)中的kΔc=0，动力学方程近似线性。因此，响应输出的主要成分是与激励载荷同频率的一次谐波分量。由于高次谐波分量的功率近似为零，高次谐波的相对功率也相应地近似为零。因此，正常叶片的衰减比近似为零。

叶片裂纹出现扩展时，动力学特性将发生变化，非线性更为显著，根据前述理论分析结果，叶片振动分量谐波相对功率将为非零值，且有望随着裂纹相对深度的增加而增加。这意味着二次谐波与一次谐波的功率比，即二次谐波相对功率，可以作为叶片裂纹的判断依据，当相对功率显著大于零时，可以判定叶片存在裂纹，否则视为正常叶片。判断是否显著的阈值设定有两种途径：一方面，根据式(23)和叶片工作频率，以及叶片强度允许的最大裂纹深度，计算得到相对功率的上限，乘以适当的安全裕度，可以得到度量相对功率是否显著的阈值；另一方面，工程上在安装正常叶片后，立即测量正常叶片的振动响应，计算得到相对功率的正常值，将正常值乘以适当的安全裕度作为阈值，也可用于判断相对功率是否显著。

这种诊断方法的优点是不再需要测量固有共振频率，避免使得叶片工作在危险的共振状态，故障判别依据只需要测量叶片二次谐波与一次谐波的幅值，可以适应叶片转速波动的实际情况，实现不同工况下的长时间连续监测。

3.2 实验台设置

为验证这种识别方法的有效性，设计了叶片振动实验，比较裂纹叶片和正常叶片的振动情况。

被测叶片类型为直板叶片，底部设置一个长方形基座方便夹持，如图3所示。

图3 裂纹叶片Fig.3 Crack blade

叶片长度L=0.112 m，宽度w=0.043 m，厚度b=0.002 m。在靠近叶片根部位置用线切割加工一个缺口，产生深度约为a≈0.000 2 m的纵贯裂纹。将参数输入ANSYS计算软件，计算得到固有频率为ω0=1 189 rad/s。扫频振动实验证明计算得到的固有频率与实际相符。叶片安装在50 kg振动实验台(型号DC-3200-36)上。激励频率设定为30～150 Hz，步长为10 Hz。

采用光学扫描法测量叶片的振动响应。与传统加速度计相比，光学扫描传感器对叶片的动态运动没有影响。因此，该方案具有较高的分辨率和精度。如图4所示，使用三个扫描测量系统(Polytec PSV-500)测量叶片不同点的振动。

图4 振动信号测试系统Fig.4 Vibration measurement system

这三个测量点图中被激光照亮为红色，如图5所示。第一个传感器测量叶片端部振动，判断叶片状态的主要数据源。第二个传感器测量叶片中部的振动，用于监控叶片振动总体幅值，防止振动过大，保证试验安全。第三个传感器测量叶片基座的振动，观察激振力的变化情况。

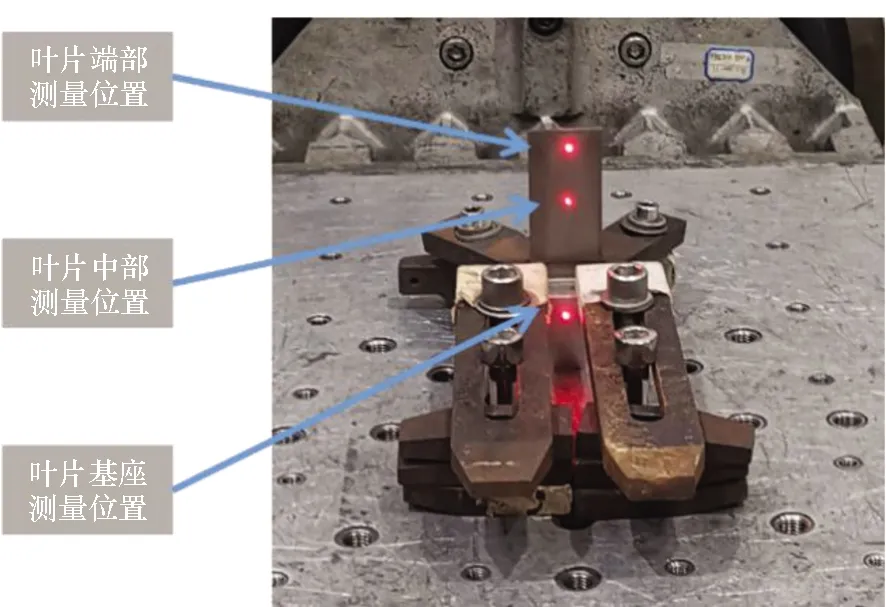
图5 测点示意图Fig.5 Picture of measuring spot

3.3 数据处理

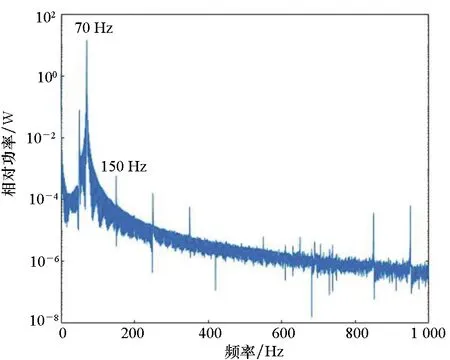
从叶片基座测得的振动频谱来看，正常叶片和裂纹叶片的基座振动频谱没有明显区别。例如，在70 Hz激励频率下，正常叶片和裂纹叶片的基座振动频谱如图6所示。频谱的主要分量均为频率等于70 Hz激励频率的一次谐波。

(a) 正常叶片(a) Normal blade

(b) 裂纹叶片(b) Cracked blade图6 叶片基座的振动频谱Fig.6 Vibrational spectrum of blade root

图7显示了相同激励下叶片中部的振动信号功率谱。从图7中可以看出，叶片中部的频率峰值比较杂乱，特别是裂纹叶片的振动谱中也难以找到明显的二次谐波140 Hz 成分。因此，叶片中部包含的诊断特征不明显。

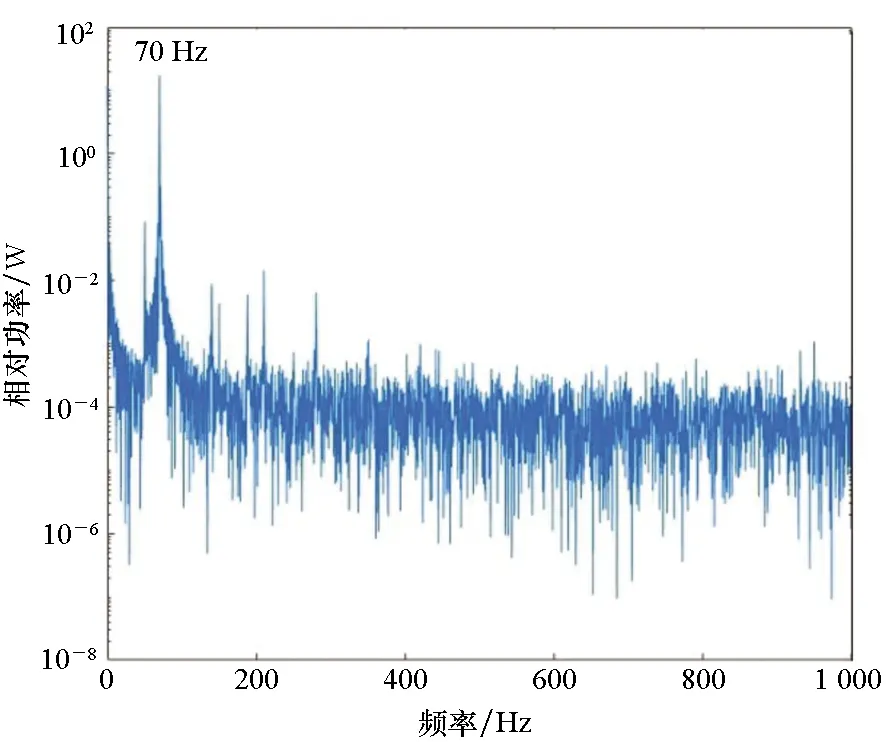
(a) 正常叶片(a) Normal blade

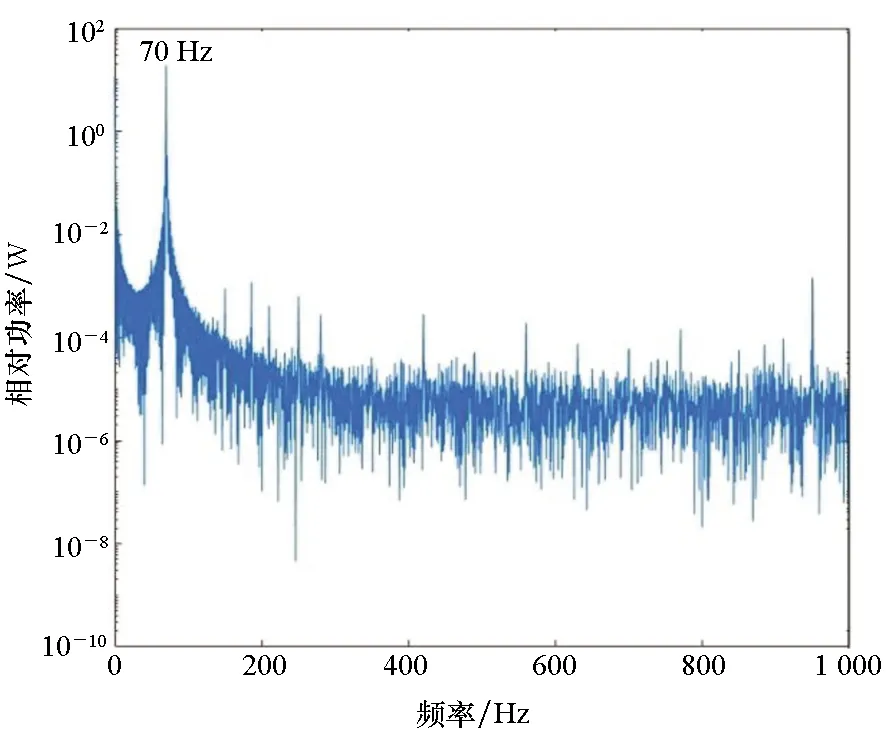
(b) 裂纹叶片(b) Cracked blade图7 叶片中部的振动频谱Fig.7 Vibrational spectrum of blade middle part

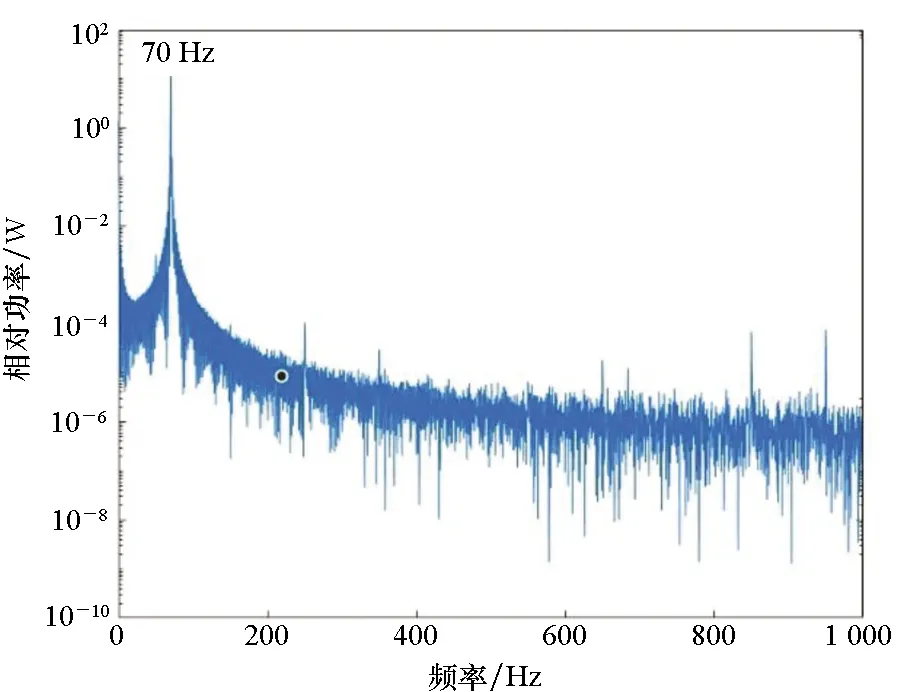
此外，裂纹叶片和正常叶片的叶尖振动响应有明显变化。图8显示了在70 Hz频率激励作用下，正常叶片和裂纹叶片的叶尖振动频谱。

比较图6(a)和图8(a)，正常叶片的叶尖振动和叶片基座振动的频谱结构非常相似，这表明正常叶片对于振动激励的反应更为接近线性。比较图6(b)和图8(b)，裂纹叶片的基座振动和叶尖振动频谱有着明显区别，从基座振动频谱可以看出，激励近似为单频激励，但是叶尖振动响应明显呈现出多频分量的组合，主要分量的频谱间隔等于激励频率70 Hz，而且140 Hz等频率处的谐波分量非常明显。从中可以看出，裂纹叶片叶尖振动对于激励明显表现为非线性响应。

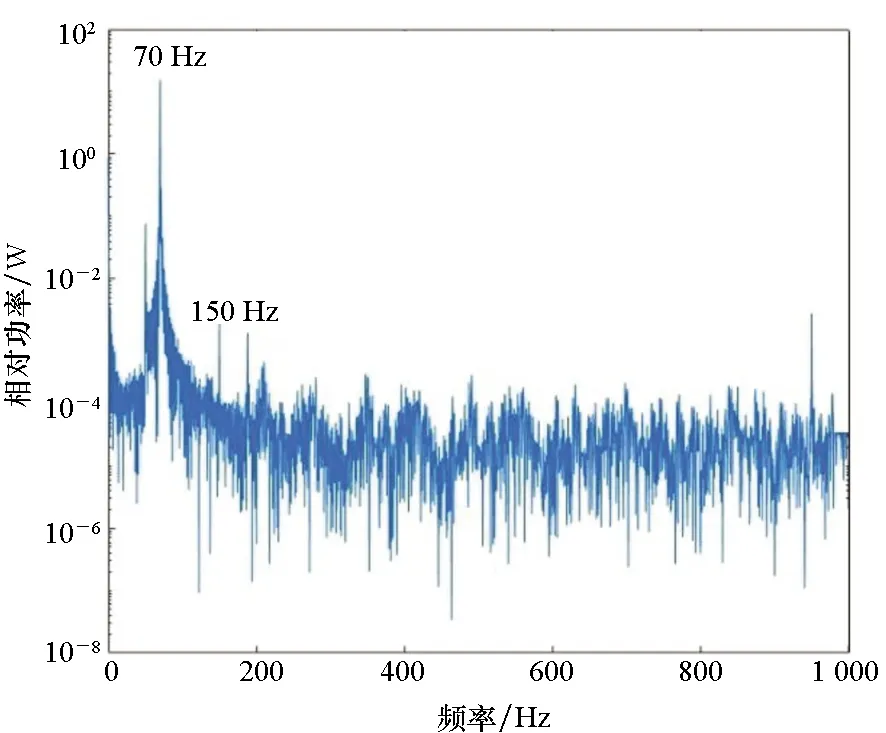
(a) 正常叶片(a) Normal blade

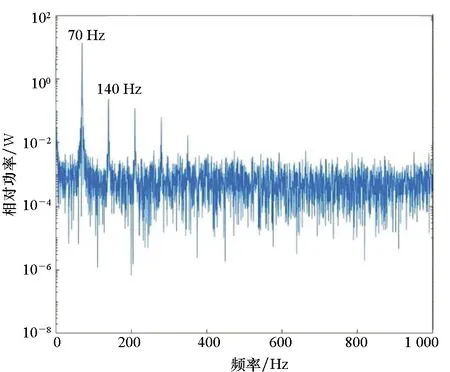
(b) 裂纹叶片(b) Cracked blade图8 叶片叶尖的振动频谱Fig.8 Vibrational spectrum of blade tip

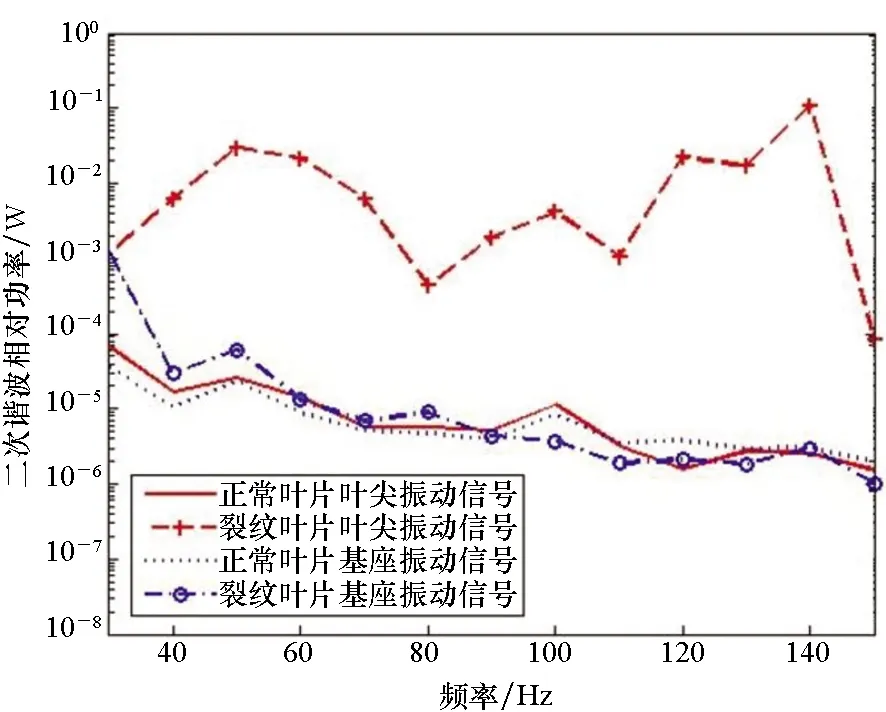
图9 正常叶片和裂纹叶片的二次谐波分量相对功率Fig.9 Relative power of the 2nd harmonics for normal and crack blades

根据所提出的叶片裂纹检测方法，计算了正常叶片和裂纹叶片的二次谐波分量相对功率，如图9所示。从图9中可以看出，基座振动信号谐波分量无论是正常叶片还是裂纹叶片，同一频率激振力作用下的二次谐波相对功率几乎相同。在本次实验参数设置的情况下，对于不同频率的激励作用，正常叶片的二次谐波分量相对功率随着激励频率的增高略有下降，但是变化并不明显。同时，在同等频率激励作用下，裂纹叶片二次谐波相对功率有明显波动，特别是在激励频率为140 Hz时，裂纹叶片的二次谐波分量达到峰值。而且，从图9中可以看出，裂纹叶片的二次谐波分量相对功率均显著高于正常叶片的相应值，这表明所提出的基于二次谐波分量相对功率的裂纹检测方法可以有效分离出正常叶片和裂纹叶片。

4 结论

本文对叶片振动的非线性响应进行了理论和实验的定量分析。根据经典梁理论，建立了叶片叶尖振动的动力学模型，分析了叶片裂纹位置、深度等因素对动力学参数的影响规律。尽管呼吸裂纹导致叶片振动方程的响应为非线性，但仍可以推导出振动响应的谐波分量功率耦合关系，这表明谐波分量功率与邻近谐波分量的功率、谐波分量阶次以及裂纹尺寸位置相关。据此提出了一种基于谐波相对功率的裂纹检测方法，并得到仿真模拟和实验验证。需要说明的是，叶片裂纹检测是个工程难题，实际应用中应该融合包括本文方法在内的多种检测方法，以提高检测的准确率和鲁棒性。