基于多信息融合的高校实验室安全预警研究
2021-12-14杨同标林王兵成艳王卫
杨同标 林王兵* 成艳 王卫
(南京理工大学泰州科技学院,江苏泰州 225300)
高校实验室是学生实践训练的主战场,是教师科研创新的重要基地,也是为社会培养实践能力强、具备创新能力的高素质技能人才的重要平台。伴随着高校对教学、科研实验室的投入力度不断加大,实验室安全事故屡见不鲜,也引起高校和社会的广泛关注。
由于实验室安全的风险的类型和成因复杂,存在的安全隐患多种多样[1-3]。在实验室安全管理研究上,专家和学者主要研究成果有:高惠玲、董鹏等提出构建一种基于危险源辨识分类实验室、基于风险评价划分实验室级别、依据管理措施及成效开展达标验收的“三位一体”的新型管理模式[4]。潘越等,设计出高校实验室危化品安全预警评价体系[5]。张煜炯,提出基于DHGF 算法的高职院校实验室安全管理评价[6]。目前,国内对实验室安全预警主要针对风险评价进行研究,而对安全预警研究较少。本文将在汲取信息融合在其他安全领域预警研究的基础上,将其应用在高校实验室安全预警机制构建上,结合了D-S证据理论与信息熵理论,以求对其高校实验室安全管理做出更为客观和准确的科学评价。
1 基础理论
1.1 扎根理论
Glaser 和Strauss 首创并发展的扎根理论是一种质化研究方法,其基本宗旨是从经验资料的基础上建立理论,从最初作为方法工具应用在社会学研究,逐渐被引入管理学研究领域[7]。
高校实验室安全信息数据来源多样,应用扎根理论,通过问卷调查、深入访谈、案例分析等方法获得第一手资料,进一步归纳提升至高一级的范畴[8]。
1.2 K-means 聚类算法
K-means 聚类算法是由Steinhuas 等人分别在不同的科学研究领域独立提出来的一种聚类算法[9]。它的核心思想是用两个数据元之间的距离来确定是否是一个簇,这个数据元与质心距离越小,相异度就越小,这两个数据元就属于一个簇[10]。
算法的具体过程:
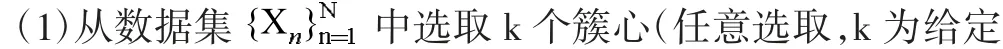

(2)对样本中的点xi,计算其与簇心cj的欧氏距离并获取其类别标号:

(4)重复步骤2 和步骤3,迭代n 次取到最优解。
1.3 信息熵理论
不同指标在评价体系中所占权重显然是不同的,Shannon 引入了信息熵的概念,解决了对信息的量化度量的问题,且在信息预测中得到了广泛的应用[11]。
算法的具体过程:
(1)设原始评价矩阵En,m其中指标个数为m,对象个数为n,先对En,m进行规范化处理,得到规范化矩阵Rn,m,步骤如下:

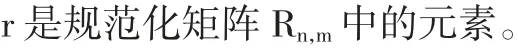
1.4 多信息融合:D-S 证据理论
D-S 证据理论是基于辨识框架的一种决策理论,辨识框架Ω 定义了一个互不相容事件的完备集合。贝叶斯推理是对Ω中的元素进行运算, 而D-S 证据理论则是对2Ω中的元素进行运算[12]。该理论给出上、下概率的概念及合成规则和不满足可加性的概率。G Shafer 在此基础引入信任函数概念,形成了一套基于“证据”和“组合”来处理不确定性推理问题的数学方法[13]。
算法的具体过程:
(1)基本概率分配函数M:

Bel 函数也称为下限函数,表示对A 的全部信任。由概率分配函数的定义容易得到

A 的不确定性由下式表示

2 基于多信息融合的高校实验室安全预警模型的建立
2.1 高校实验室安全预警指标的确立
安全预警模型的确立离不开监测指标的确立,本文从安全监管视角,运用扎根理论的方法,采用访谈、问卷等形式向高校实验室管理人员等20 多人进行了咨询,对高校实验室安全影响因素进行了识别。共设置4 个主范畴作为预警一级指标、并从44 个相关概念中提取16 个范畴作为预警二级指标,预警指标体系如图1 所示,其中A1、A3、A4 为正向指标,数值越大越安全,评分方法参考文献[5],A2 为负向指标,数值越大越危险。

图1 高校实验室安全预警指标体系
2.2 多信息融合预警模型的建立步骤
信息融合技术又被称之为数据融合,其目的是通过多源信息的高效融合避免单指标评判的误差性[14]。影响高校实验室安全的因素种类繁多,如何将多信息进行有效的融合是安全预警是否科学的关键。
本文通过对某高校的调研,选择S1、S2、S3、S4、S5 五个实验室作为分析样本,通过以下步骤完成对多信息融合预警模型的建立,流程图如图2 所示。
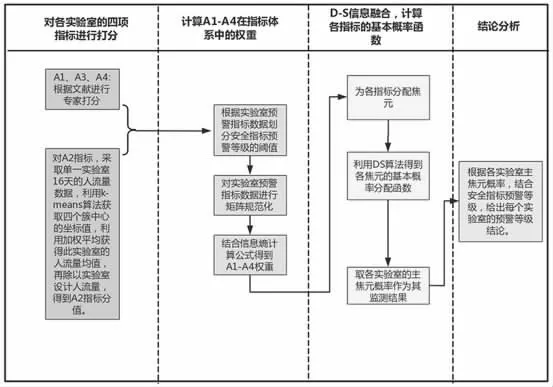
图2 高校实验室多信息融合预警模型建立流程
(1)通过2.1 预警指标体系的建立,可对每个实验室的具体情况进行打分。A2 指标选取K-means 算法,对一段时间内的实验室流量数据进行聚类计算,得到簇中心数据后在对各中心点进行加权平均,以此作为该实验室的人流量数据。A1、A3、A4 指标则可以通过专家打分获得相应分数。
(2)不同指标权重不同,本文利用已有数据将安全等级分为四级分别是无警、轻警、中警和重警,将各个指标的阈值对应安全级别进行划分,再利用信息熵计算各指标权重。
(3)根据D-S 理论设置不同焦元对应不同指标,通过D-S计算规则得到多个实验室数据融合后的基本概率分配函数,选取主焦元作为预测结果。
3 基于多信息融合的高校实验室安全预警模型的应用
3.1 预警指标的确定
本文通过对某高校的调研,选择S1、S2、S3、S4、S5 五个实验室作为分析样本,其中A2 指标的分值获取过程如下:
(1)以实验室S1 为例,选取其16 天的人流量数据进行聚类分析。
(2)结合2.2 中K-means 算法对S1 数据进行聚类处理,其中横坐标为时间(1-8 节课),纵坐标为人数(流量),k 值取4,聚类结果如图3 所示。

图3 K-means 聚类后数据
(3)聚类后得到四个簇中心,坐标如表1 所示,其余实验室同理。

表1 人流量数据簇心坐标表
实验室S1 的设计人流量70,对四个簇心点加权平均,得到实验室1 对于人流量指标的分数0.60,其他实验室同理,A2 指标的打分情况如表2 所示。

表2 各实验室人流量指标得分表
结合3.1 中对A1、A3、A4 指标的打分情况,可以得到实验室S1-S5 的预警指标得分情况,结果如表3 所示。
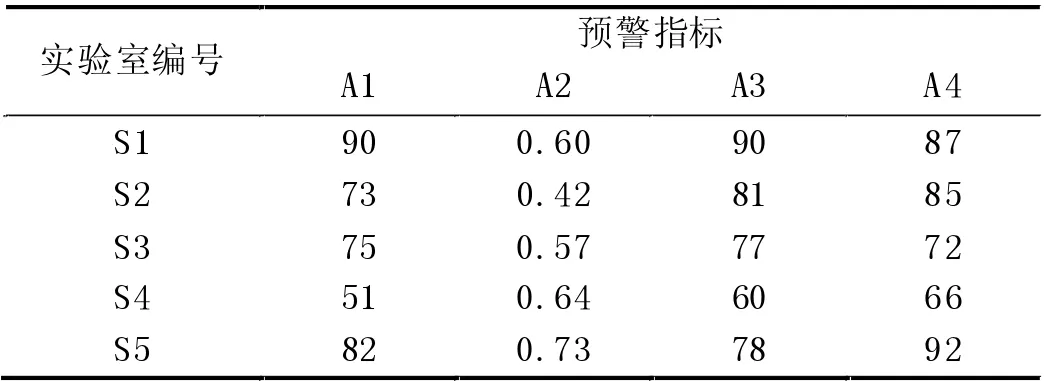
表3 实验室S1-S5 预警指标数据
3.2 分配指标权重
(1)预警指标阈值的确定:
根据已有的实验室安全评级制度,结合表3 中的实际预警指标数据对阈值进行划分,将样本实验室安全等级分为四级,结果如表4 所示。
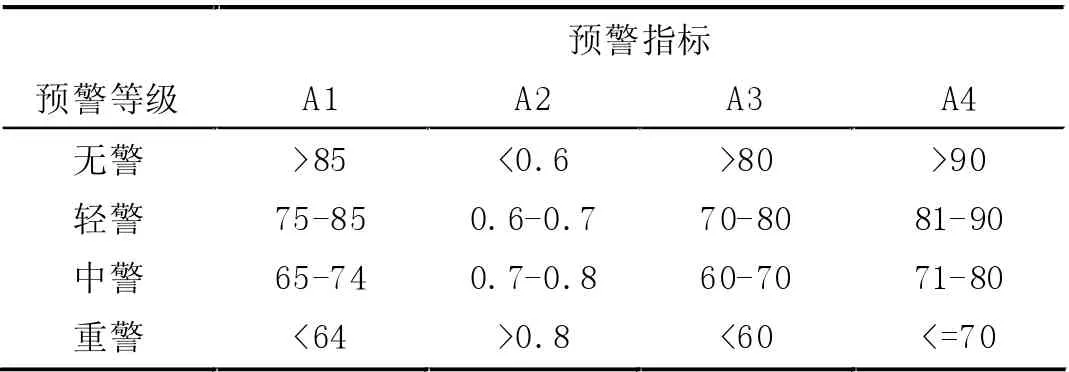
表4 实验室安全指标预警等级表
(2)原始预警数据的规范化:
设原始评价矩阵En,m 其中指标个数为m,对象个数为n,先对En,m 进行规范化处理,规范化后矩阵如表5 所示。
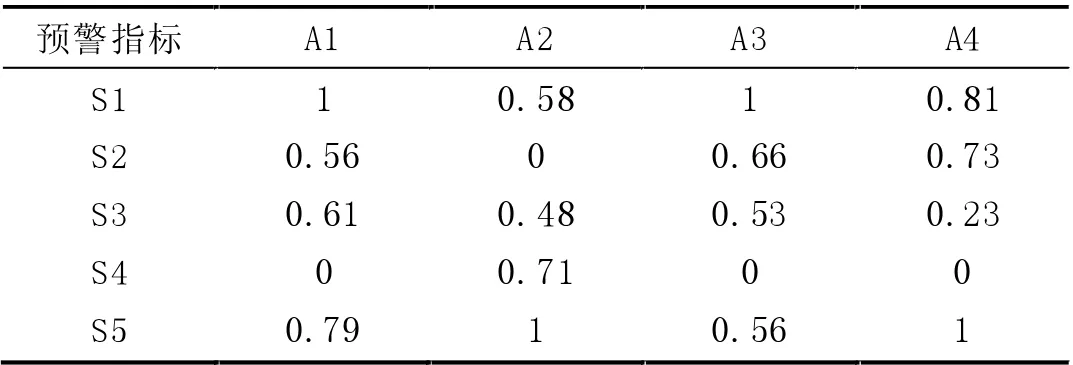
表5 预警数据规范化矩阵
(3)权重计算
对表5 中的数据利用信息熵算法求各指标在综合体系中所占的权重。公式(4)计算指标j 熵值Hj,由式(5)计算熵权(即权重ωj),结果如表6 所示。

表6 高校实验室安全预警指标权重
3.3信息融合后的基本概率函数
在本案例中,针对不同的指标选取三个元素A、B、C,用M(A)、M(B)、M(C)、M(AB)分别对应无、轻、警、警四个等级的基本概率分配函数,由表3 的指标数据和表4 的警限阈值,得出每个实验室不同的预警指标所对应的基本概率分配函数焦元[15],如表7 所示。

表7 样本实验室预警指标对应的焦元
根据表6 给出的权重,加权合成基本概率分配函数,结果如表8 所示。
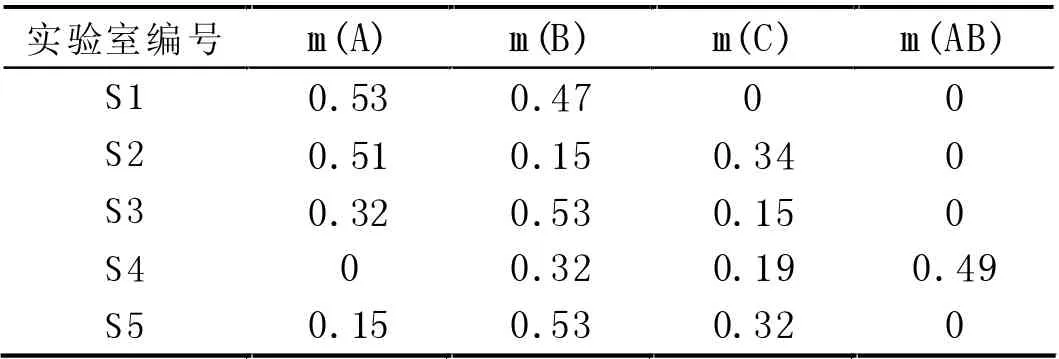
表8 基本概率分配函数
根据公式(8)合成5 个基本概率分配函数,结果如表9 所示。

表9 实验室融合结果
3.4 预警判定
根据表9,我们可以选取四个证据中的主焦元作为分析依据。根据前文叙述的焦元与预警等级的映射关系,对五个样本实验室的预警判定结果如表10 所示。

表10 高校实验室安全预警结果
3.5 融合结果分析
通过表10 可以得出结论:实验室S1-S2 为无警状态,实验室S3、S5 为轻警状态,实验室S4 的预警等级为重警状态。结合表2 的打分数据,可确定出实验室S4 的4 项指标的预警等级分别为重警、轻警、中警、重警,该结果与表10 给出的实验室S4 安全等级为重警的结论完全吻合。说明基于D-S 证据理论的多信息融合模型在高校实验室安全预警方面具有很好的可行性与适用性。
4 结论
4.1 本文依托多信息融合技术,以扎根理论构建高校实验室安全预警指标体系,运用D-S 证据理论与信息熵理论实现了不同信息源、不同量纲信息的有机融合,建立预警融合模型输出预警结果,避免了单一指标预警的片面性[15]。
4.2 通过对样本实验室的四项预警指标数据进行打分,通过k-means 算法对人流量数据进行聚类,克服了实验人数不固定的缺点,又通过信息熵确定了各指标在预警系统中的权重。最后结合D-S 证据理论将各项证据融合,给出预警评价。实证表明,预警判定结果客观的反映了各实验室的风险类别,与真实情况吻合,对高校实验室安全预警管理有一定的指导意义。
4.3 本文也存在不尽完善之处。虽然D-S 证据理论多用于信息融合领域,但其受限于证据的独立性,在很多情况下此条件不易成立;另外D-S 的合成算法,其合理性和有效性还存在一定的争议。
