状态切换对激光惯导系统的影响研究
2021-12-14沈士辉夏卫星雷明良
沈士辉 夏卫星 雷明良
(海军潜艇学院,山东青岛 266000)
双轴旋转激光惯导系统采用捷联式惯导力学编排,将激光陀螺和加速度计为主构成的惯性测量组件与载体相对固联,利用惯性测量组件信息处理模块采集、处理惯性元件测量信息,经导航计算机解算,输出载体姿态、速度、位置等导航信息[1-2]。系统采用双轴调制技术,通过转位机构带动惯性测量组件实现周期性调制运动,并实现载体机动隔离,使得调制周期内惯性测量组件的标定误差和惯性元件误差引起的导航误差积累量为零,提高长航时导航精度[3-4]。
基于双轴旋转调制的捷联惯性导航系统工作在水平阻尼状态时,能够很好地抑制惯性器件的常值误差和系统中的振荡性误差,进而提高系统的导航定位精度。但是,水平阻尼网络虽然可以将双轴旋转调制式捷联惯导系统中的舒勒周期和傅科周期振荡分量衰减下来,但同时也破坏了舒勒回路的加速度无干扰条件。在阻尼状态切换时,由于打破了原来的平衡状态,旋转调制式捷联惯导系统在进行阻尼状态切换时会产生超调现象。本文针对状态转换对双轴旋转激光陀螺惯导系统性能影响开展分析。
1 双轴旋转激光陀螺惯导系统调制机理
与纯粹捷联惯导系统相比,双轴激光陀螺惯导系统的精度要大为提高,这尤其适合于舰船、潜艇等需要长航时自主导航的运载体[5-6]。同时,与传统高精度平台式系统相比,旋转式系统的体积、购买成本和维护费用都大大减少。由于传统的稳定平台是作为导航计算的参考而对其精度和可靠性等要求非常严格,而双轴惯性导航系统采用了与捷联式系统一样的数学平台,转动控制结构仅仅起到平均漂移的作用,即使转位机构停止运转,导航系统也能够工作,只是精度有所降低。从系统算法来看,双轴激光陀螺惯导系统是在捷联惯导系统基础上发展而成,其系统算法与捷联算法类似,仅转动控制、姿态输出等部分有所不同,更容易实现。双轴激光陀螺惯导系统的原理图如图1 所示。
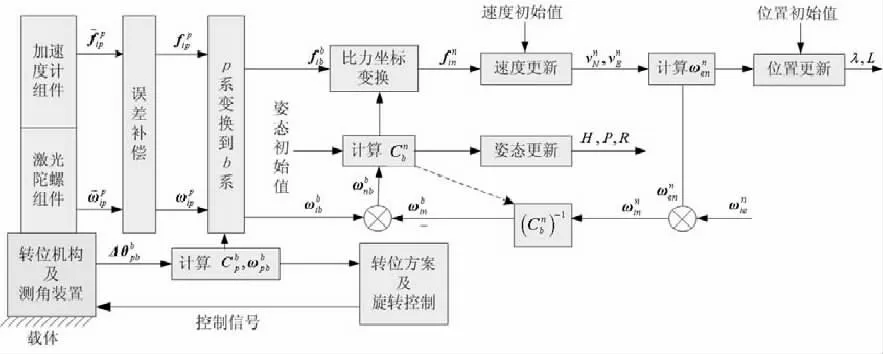
图1 双轴激光陀螺惯导系统原理图
在没有引入旋转调制情况下,陀螺和加速度计在载体坐标系(b)下输出的角速度ω˜bib和加速度信息f˜bib满足(为方便分析,假设载体坐标系与地理坐标系重合,即Cnb=I):


式中,ω 为旋转调制角速度。
由式(7)可知,与旋转轴垂直的平面上的陀螺常值漂移被调制成正余弦形式,而旋转轴上的陀螺常值漂移则不受调制;对式(7)在一个旋转周期内进行积分,与旋转轴垂直平面上的陀螺常值漂移引起的数学平台误差角被平均掉,旋转轴方向的陀螺常值漂移仍按照原规律传播。加速度计零偏的调制机理和分析方法与陀螺常值漂移相同。
2 双轴激光陀螺惯导系统误差方程
由上述分析可知,与传统捷联惯导系统相比,在旋转调制式系统中,惯性元件的常值漂移本身并没有改变。惯性原件常值漂移引起的导航解算误差在一个周期内会相互抵消,所以惯性元件的所有漂移仍然会表现在系统误差方程中。
由式(7)及常规捷联惯性导航系统误差方程,经推导得到双轴激光陀螺惯导系统的误差方程如下式所示。
速度误差方程:
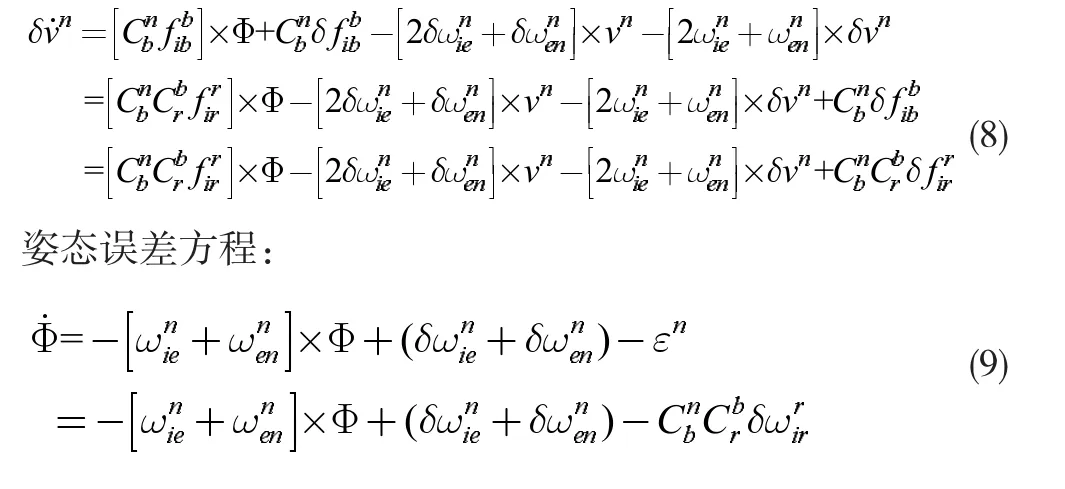
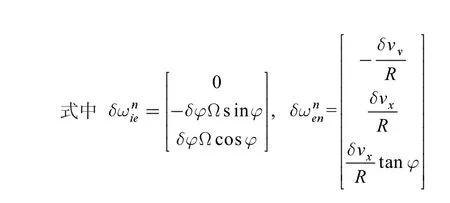
3 阻尼状态切换对双轴激光陀螺惯导系统的影响分析
当双轴旋转调制式捷联惯导系统处于无阻尼状态时,数学平台旋转角速度可以表达为如下形式




由式(14)可知,系统在阻尼状态切换后,数学平台旋转角速率ωcy(t+0)较切换前发生了突变。阻尼状态切换对数学平台旋转角速率产生的影响可以等效为一种外加干扰Δ,而且该外加干扰量不仅与水平阻尼网络Hx有关,而且还与t0状态切换时刻双轴旋转捷联惯导系统速度误差Vrx-Vcx有关,即状态切换时刻速度误差越大,引入的外加干扰量Δ 越大。另一方面,由于数学平台旋转角速度直接参与到捷联矩阵的更新解算中,所以阻尼状态切换导致的数学平台旋转角速度的突变必然导致姿态角解算值发生超调,进而导致系统速度以及位置输出发生超调。
4 仿真实验
为验证阻尼状态切换对于双轴旋转捷联惯导系统的影响,利用MATLAB 进行仿真试验。双轴旋转捷联惯导系统旋转方案采用十六位置转位方案,具体旋转方案如图2 所示。
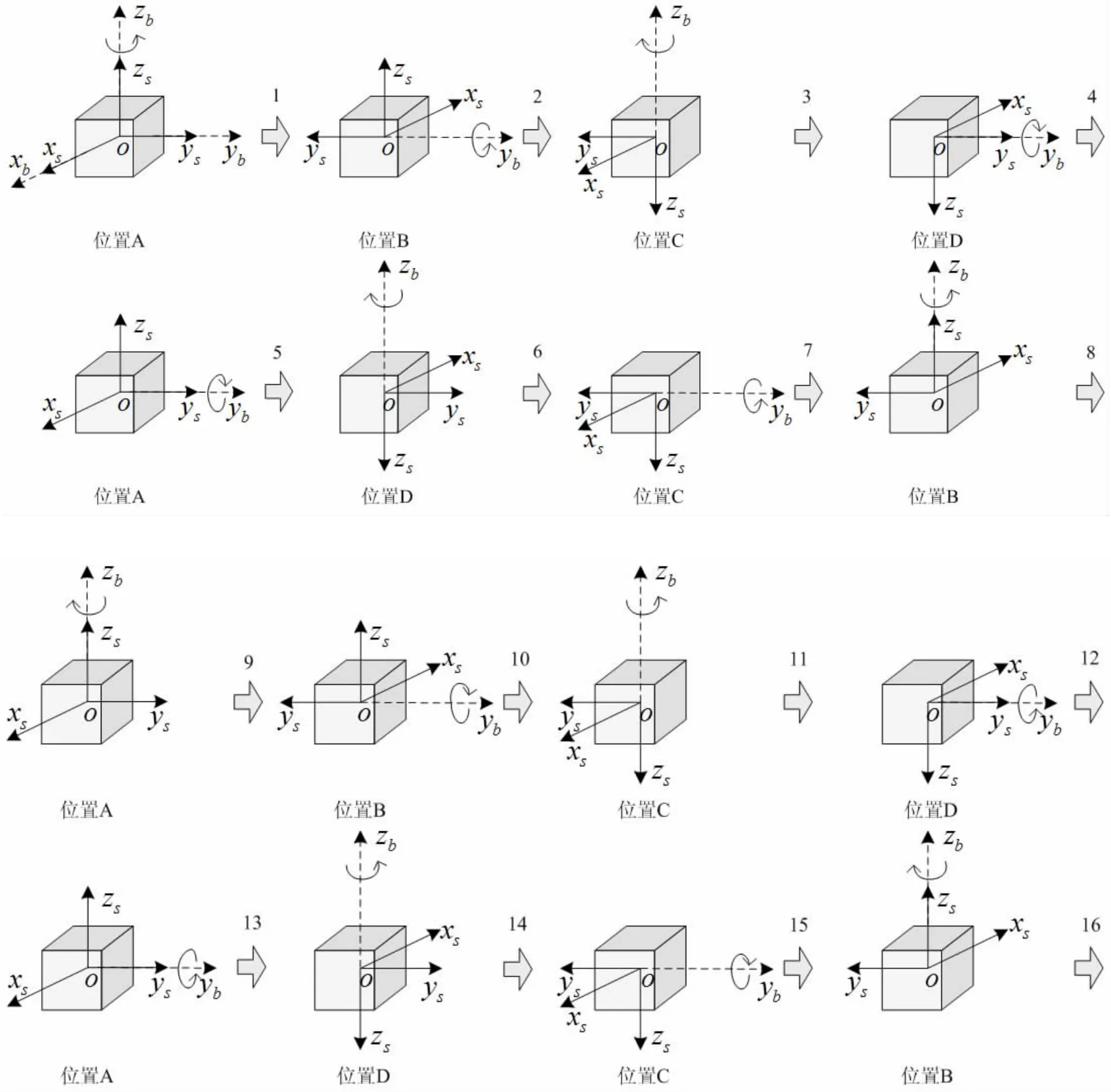
图2 双轴旋转调制式捷联惯导系统转位方案
仿真环境设置如下:
假设载体匀速直航,航速为15 节;陀螺漂移为0.005o/h,加速度计零偏为10-4g;不考虑初始对准误差,载体三轴姿态运动规律为:
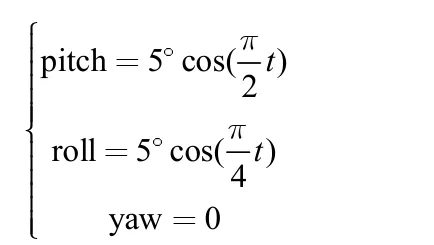
仿真时间设置为12 小时,十六次序转动方案中,设定每个转动过程消耗的时间均为12s;通过分析双轴转停时间对误差补偿的影响,设定每个固定位置停顿时间为60s;在第6 小时进行无阻尼状态与外水平阻尼状态之间的阻尼状态切换,仿真结果如图3 所示(只给出水平姿态角误差)。
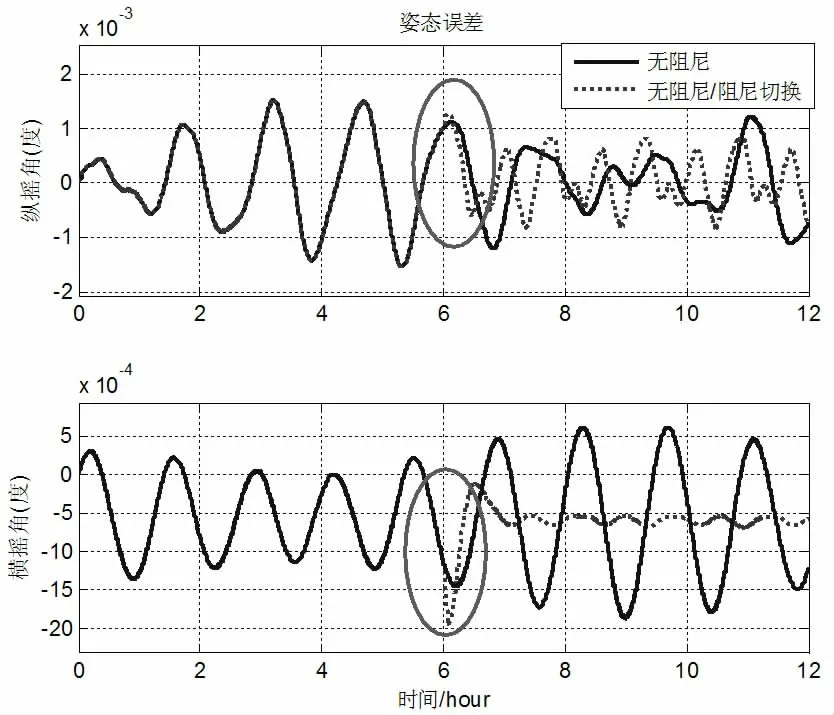
图3 水平姿态角误差
根据仿真结果可以看出,在第6 小时进行阻尼状态切换时,与前面分析一致,两个水平姿态角误差都发生超调现象,但是该超调性动态误差可以被阻尼掉。通过以上分析可知,阻尼状态切换的确会给双轴旋转激光陀螺惯导系统输出带来影响。为了减小阻尼状态切换对于双轴旋转激光陀螺惯导系统的影响(主要是引起动态误差),可以在载体惯导速度误差较小时进行阻尼状态切换。
5 结论
论文从双轴激光陀螺惯导系统惯性器件误差调制机理着手,给出了惯导系统误差方程,在此基础上,分析了阻尼状态切换对双轴激光陀螺惯导系统的影响,给出了状态切换对系统导航精度的影响模型,并进行了仿真实验。理论与实验结果表明,阻尼状态切换导致的数学平台旋转角速度的突变必然导致姿态角解算值发生超调,进而导致系统速度以及位置输出发生超调,若降低切换导致的超调影响,可在载体速度误差较小时进行阻尼状态切换。
