高压透平动叶非轴对称端壁优化设计

朱能杰，张 方，竺晓程，沈 昕，杜朝辉

(1.上海交通大学 机械与动力工程学院，上海 200240；2.上海汽轮机厂有限公司，上海 200240)

透平内二次流以及边界层黏性摩擦作用引起的端部损失占到总损失的30%[1]。对于负载大、展弦比小的高压级透平，端部损失比例可达50%以上[2]。非轴对称端壁设计是一种通过调整端壁结构，从而改变局部流动的设计方法，已被研究者证实可有效控制二次流，降低流动损失[3]，并广泛应用于透平等叶轮机械中[4]。Brennan等[5]系统地总结了非轴对称造型原理，并在TRENT500透平的应用中证实了其可有效提升高压级级效率。Snedden等[6]在设计工况和偏离设计的多个工况下，通过透平实验证实了其改善流动的效果。李军等[7]将该设计思想应用于高负荷透平的结构设计中，分析得出其改进气热性能的作用机理。陆泽帆等[8]研究了考虑动叶轮缘泄漏时，采用非轴对称端壁对于透平冷却与流动的影响。

近年来基于优化算法与数值计算的优化设计方法成为研究者关注的焦点[9]。Praisner等[10]采用基于梯度的优化算法，得到了多种端壁非轴对称方案。高增珣等[11]基于ISIGHT平台设计了一套透平叶栅端壁优化体系。孙皓等[12]基于双控制曲线端壁造型方法建立了一套优化设计方法。唐慧敏等[13]开发了一种以网格变形技术为核心，来对端壁进行模块化自动寻优的优化设计系统。

本课题组自行设计了集成非轴对称端壁造型、数值计算与代理模型的优化系统[14]。刘昊等[15]将其应用于Durham叶栅的设计改进中，结合实验测量与数值模拟计算，分析对比内部流动的结果，证实了优化的有效性。本文对该系统进行了改进，将其应用于某型高压透平的第1级，对其动叶端壁进行优化，得到了最优设计方案。通过数值计算证明了合理的非轴对称造型方法可改善透平内部流动，提高透平级效率，并对其减小二次流的机理进行了分析。该项研究成果具有广泛的工程应用前景。

1 研究对象与数值方法

本文的研究对象为某型高压透平的第1级，该级轮毂半径为395 mm，表1给出了该级叶片的参数。其中S1为静叶，R1为动叶，Cax为轴向弦长。

表1 叶片参数

对该级动叶的轮毂面进行非轴对称设计，其余保持圆柱端壁。网格划分使用NUMECA软件，进出口分别延伸了2倍S1的Cax与2倍R1的Cax。考虑优化效率与计算精度的平衡，最终网格数确定为84万，图1为计算网格示意图。数值计算采用ANSYS CFX软件，工质为水蒸气，采用k-ε湍流模型，进口给定总温总压条件，出口边界给定流量条件。

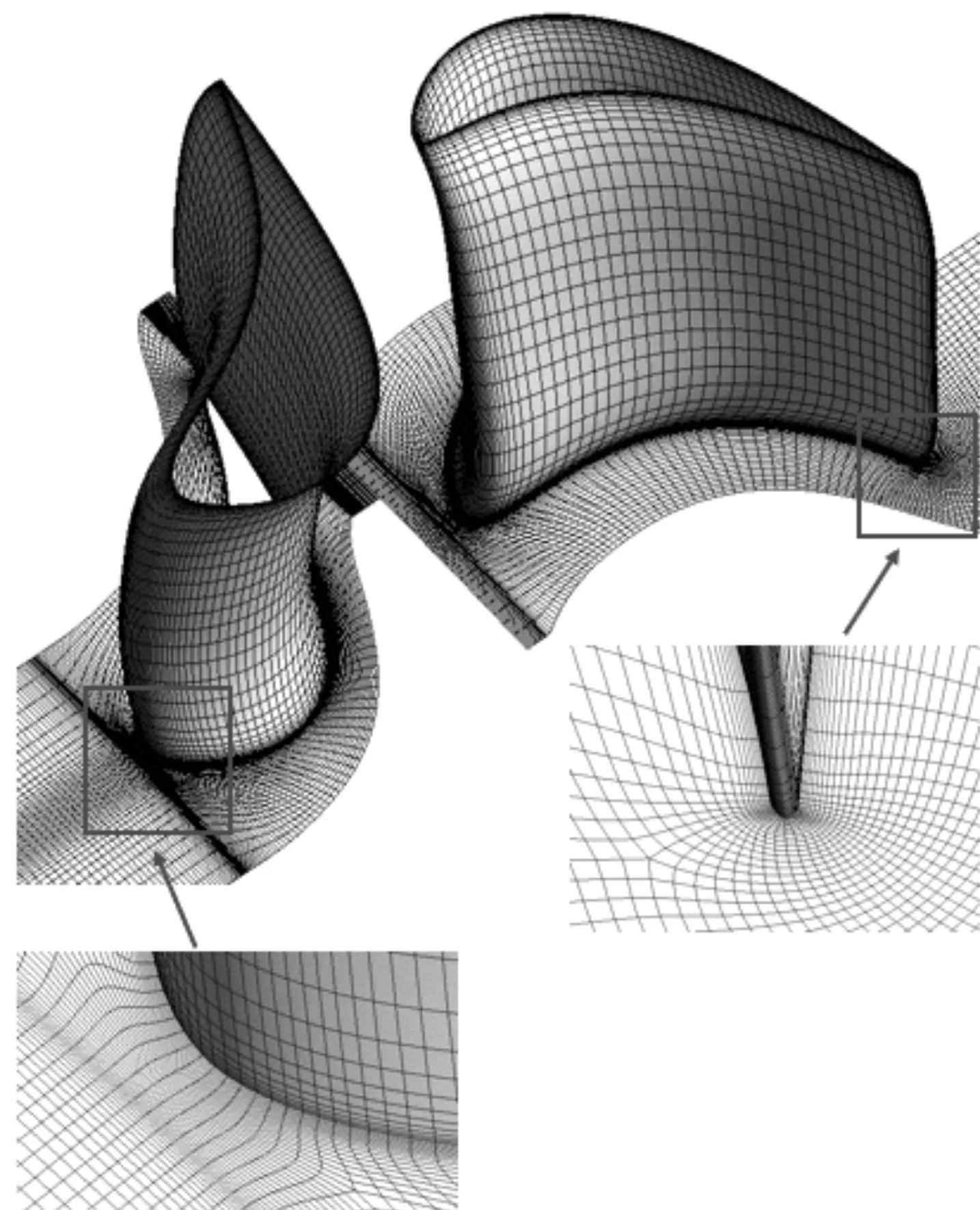
图1 计算网格示意图

2 优化设计方法

图2为本文采用的优化设计系统流程图，通过Matlab实现该系统各模块间的数据传输，调用脚宏命令与DOS脚本，从而在优化的过程中驱动NUMECA、ANSYS CFX软件按预设参数自动进行网格划分、数值计算与后处理。

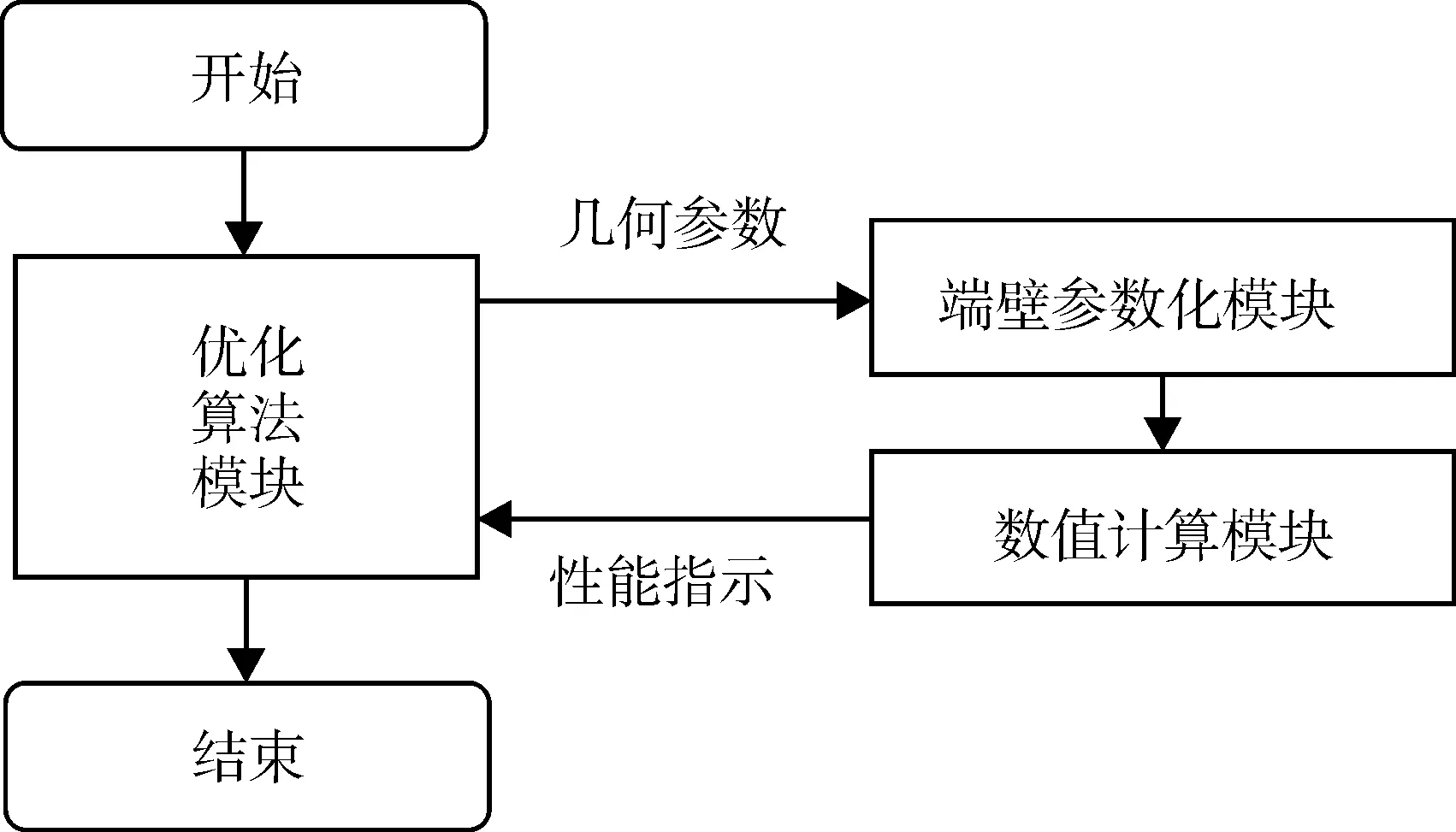
图2 优化系统设计流程

在端壁参数化模块，采用双扰动曲线方法，在轴向和周向设置参数化的控制曲线，相乘得到设计区域的几何扰动分布，将该扰动分布叠加在原端壁结构上，即可得到非轴对称模型。几何扰动表达式如下：

δr=δr(x)·δr(y)

(1)

式中：δr为端壁径向变化值；δr(x)、δr(y)分别为轴向曲线与周向曲线的径向扰动变化值。

在轴向选用3次B样条曲线，综合考虑寻优空间与寻优效率，轴向曲线设有10个控制点。在周向采用带相位变化的正弦函数，其周期性的特点可以使得流道面积在端壁优化后基本保持不变。各自表达式如下：

(2)

δr(y)=sin(2πy+θ)

(3)

式中：Ni,3(x)为3次B样条基函数；Pi为曲线控制点的集合；θ为周向的相位变量。

为保证端壁设计区域与其余部分交接处的平滑过渡，前后各设2个端点且固定不变，故轴向有6个几何参数，周向有1个几何参数，控制曲线如图3所示。

通过改变各几何参数的值可以得到对应的非轴对称端壁几何造型，如图4所示。非轴对称端壁设计区域的周向范围为相邻叶片的端壁压力面之间，轴向范围以叶片前缘轴向位置到叶片尾缘轴向位置为界。

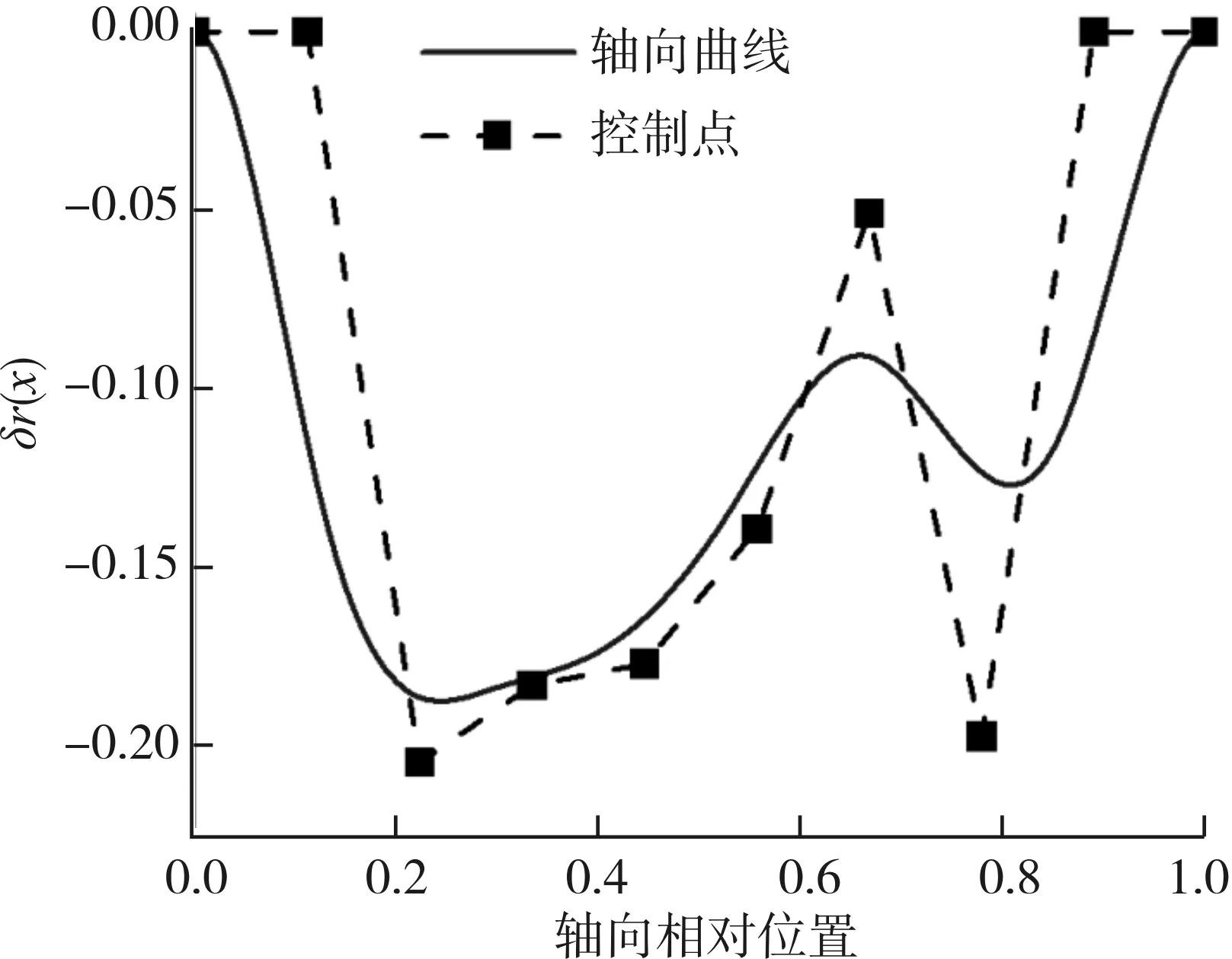
(a) 轴向控制曲线

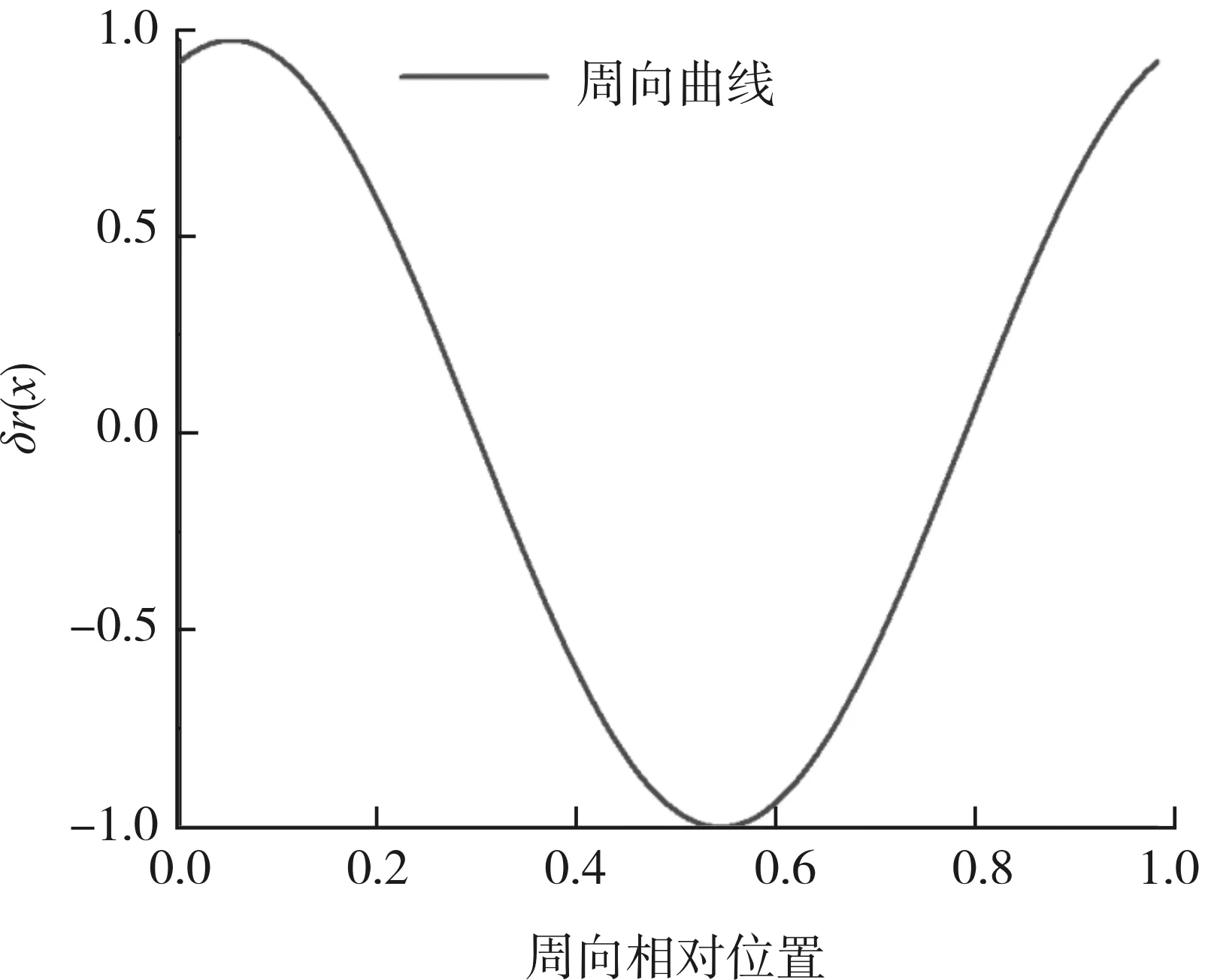
(b) 周向控制曲线

图4 非轴对称端壁造型示意图

对于优化算法模块，本文采用一种自适应的Kriging代理模型[16]，其相比于原方法的改进在于，使用微种群遗传算法替换模式搜索算法，对相关参数向量进行寻优，以解决原方法受初值影响过大的问题。

首先基于均匀设计方法建立初始几何参数集，根据本文几何参数数目，选用U18(187)均匀设计表。调用模块实现自动几何生成与数值计算，返回性能指标值。本文选取的性能指标为该级出口二次流动能系数，定义式为：

(4)

式中：v1为进口速度矢量；vrad为速度矢量的径向分量；vsec为设计流动平面上二次流矢量的分量。vsec定义式为：

vsec=vsin(α-αmid)

(5)

式中：α为实际流动角；αmid为50%叶高周向平均流动角。

基于Kriging代理模型初步建立几何参数与性能指标的对应关系。采用EI(Expected Improvement)函数用以确定模型下一步迭代的校正点，该方法兼顾了预测最优值与预测标准差，平衡了局部和全局寻优能力。将校正点加入样本集中，计算对应的性能指标，不断更新模型，最终得到最优设计方案。

3 结果分析

采用如前所述优化系统，进行了200步优化迭代。表2给出了原型方案Ori与最终得到的优化方案Proj的流动参数对比。

表2 优化前后流动参数对比

其中，αdev为实际流动角α与动叶50%叶高周向平均流动角αmid之间的差值绝对值，定义式为：

αdev=|α-αmid|

(6)

η为透平级的等熵效率，定义式为：

(7)

式中：Tt2和Pt2为该级出口处总温、总压；Tt1和Pt1为该级进口处总温、总压。

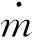
图5为优化后动叶轮毂端壁几何变化示意图，δr正值表示上凸，负值表示下凹。可见端壁出现了两处特征区域：其一是在接近透平吸力面侧的形状较宽的下凹区域，吸力面肩区附近出现最大峰值，为叶高的6.17%；其二是接近尾缘的流道中部的上凸区域，体现出沿叶片转折方向的长窄的分布形式，该区域的峰值为叶高的3.70%。由于确保了轴向曲线前后控制点为0，因此凹陷与凸起区域与保持轴对称端壁的区域平滑过渡，未出现突变等异常几何构造情况。

图5 优化结果几何示意图

图6给出了动叶轮毂端壁优化前后的静压分布对比。可见端壁的凹凸可以改变流线曲率，进而使得凹陷处局部压力上升，凸起处压力降低。图4的非轴对称端壁分布形式使得在透平通道的前半段，凹陷端壁附近出现了高压区域，由于端壁凹陷贴近吸力面一侧，因此相比原型，周向的压力梯度减小。该压力梯度是动叶轮毂附近的边界层低能流体发生迁移的重要驱动力，驱使其从压力面向吸力面流动。该驱动力的减弱可有效抑制压力面马蹄涡的发展与低能流体的迁移，影响通道涡的强度，从而减小流动损失。在通道的后半段，相比原型端壁，凸起区域导致在尾缘吸力面侧的低压区的范围与峰值均明显增大，这使得压力梯度由周向向流向偏转， 从而有效降低了二次流强度，减小了出口流动偏离角，这样可以有效提高叶片出口流动的均匀性。

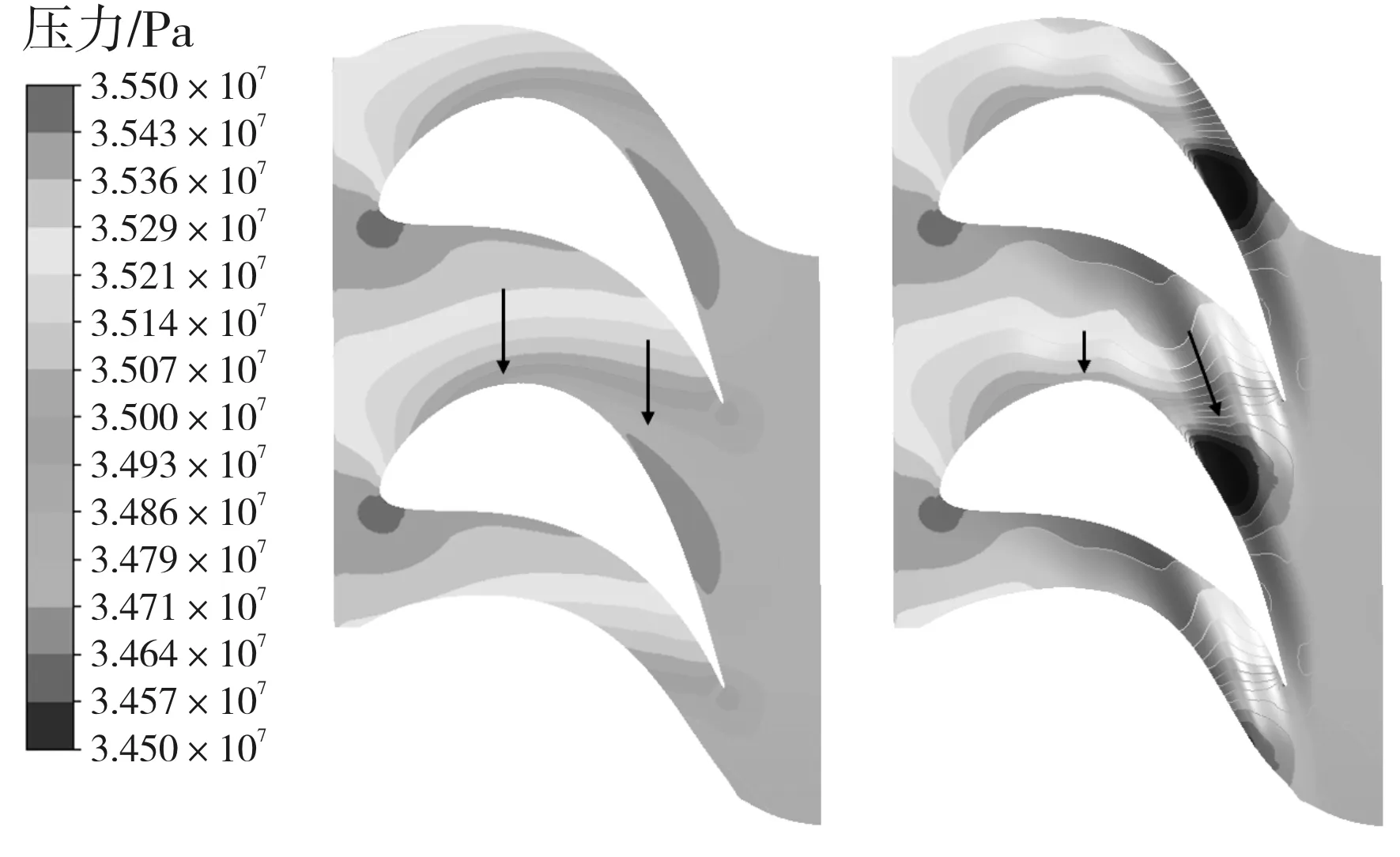
图6 优化前后端壁静压分布对比

图7沿轴向等距给出了5个截面上的流向涡量系数CΩ云图，沿来流方向逆时针旋转涡量为正，图6仅给出流向涡量为正的区域，以捕捉通道涡和压力面马蹄涡两个主要的损失来源涡系的强度变化，CΩ定义式为：

(8)

式中：Ωs为流向涡量。其定义如下：

Ωs=Ωxcosαmid+Ωysinαmid

(9)

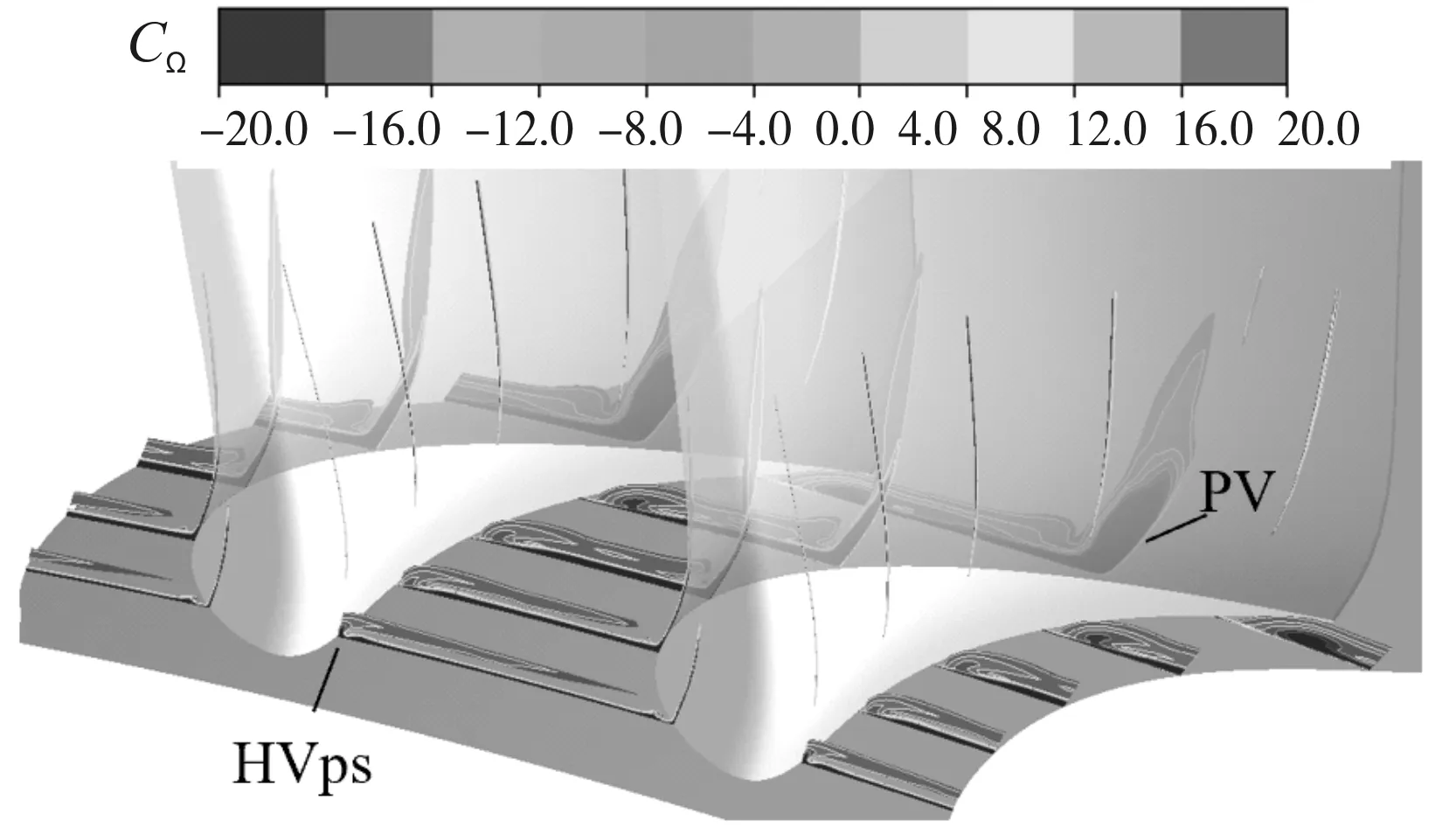
(a) 优化前

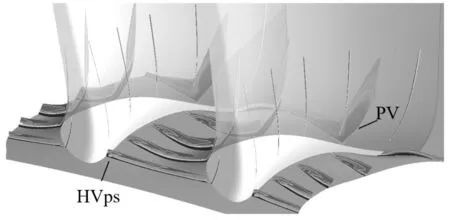
(b) 优化后

可见对于原型端壁，在叶片前缘位置出现了来流边界层的分离，由于存在周向压力梯度，马蹄涡的压力面分支HVps向吸力面侧移动，边界层附近的低能流体随之移动至吸力面附近，最终离开端壁，形成通道涡PV。优化后通道前段的周向压力梯度的降低使得压力面马蹄涡发展受阻，可见其在中间截面的涡强度以及裹挟的边界层低能流体的数量与强度均明显降低，到达吸力面的位置推后，影响了成型的通道涡的强度。但是通道后半段周向压力梯度相比原型有所提升，这虽然有利于出口流动角的均匀性与二次流的降低，但同样促进了流道后半段通道涡的发展，最终形成的通道涡强度相比于原型略有上升。

图8为距动叶尾缘25%Cax处的出口截面上，优化前后的CΩ分布云图。可见出口截面形成通道涡、壁面涡、角涡与低能流体的涡系结构，分别对应于图中的A、B、C、D 4处流向涡量系数峰值区域。比较优化前后4处区域的峰值大小与涡影响范围可以发现，轮毂处的端壁变动主要影响50%叶高以下区域，对近机匣部分的影响很小。优化后更多的低能流体停留在端壁附近，表现为B区域的范围扩大，A区域对应的通道涡强度相比原型略有提升，但D区域的角涡与C区域的壁面涡强度明显降低，从而有效降低了流动损失，透平性能得到提升。

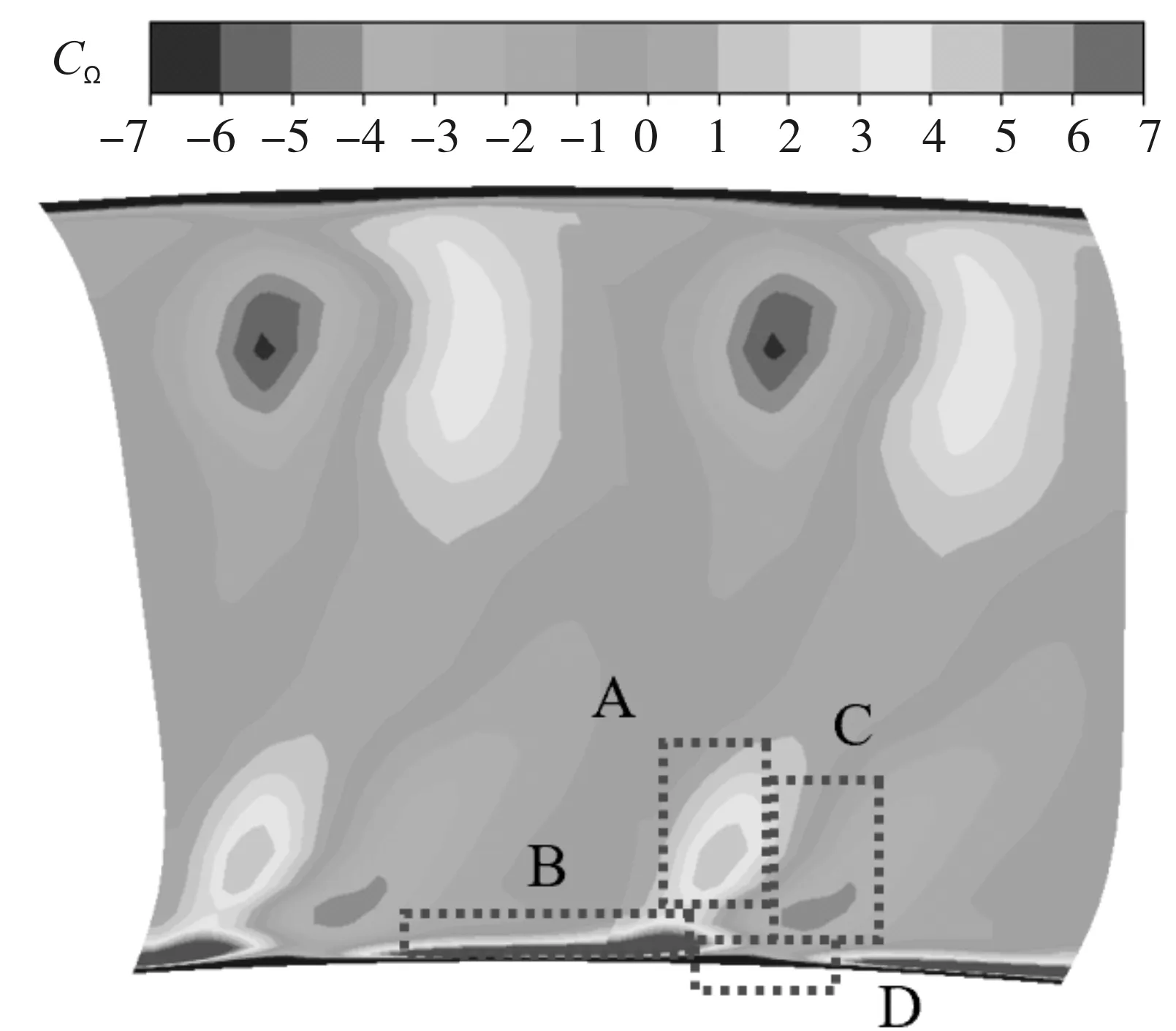
(a) 优化前

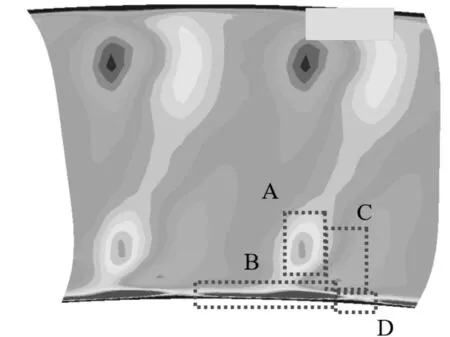
(b) 优化后

图9为距动叶尾缘25%Cax处的出口截面上，优化前后二次流动能系数Cske与流动角α的周向平均值沿径向分布图。可见与流向涡量的变化趋势相对应，优化后二次流动能系数在接近机匣部分的变化并不明显，但50%叶高以下即接近轮毂一侧，二次流动能系数在各叶高位置显著降低，峰值降低了19.9%，仅在20%～30%叶高处由于通道涡强度的增大，该处二次流动能略有提升。与二次流动能系数的变化相一致，相比于原型透平，优化后50%叶高以上流动角未出现明显的变动，优化后的流动角最小值降低了3%，欠偏转角度与欠偏转区域均显著小于原型透平，说明优化后出口流动角的均匀性得到了有效提升，轮毂端壁侧欠偏转现象得到了显著改善，并且能够在一定程度上改善透平下游叶片的进口流程特征，对于提高透平整体性能和流场是有利的。

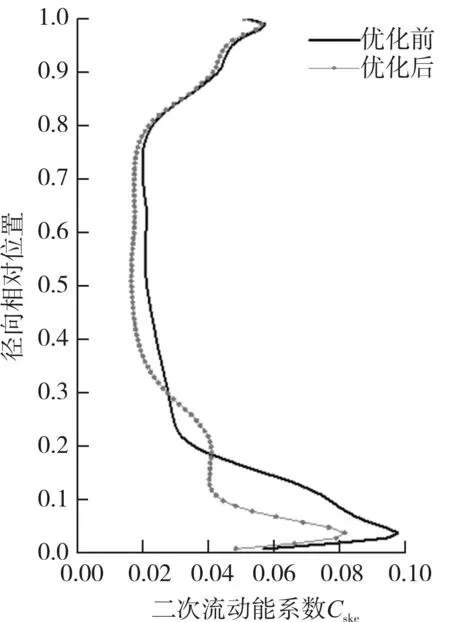
(a) 二次流动能系数

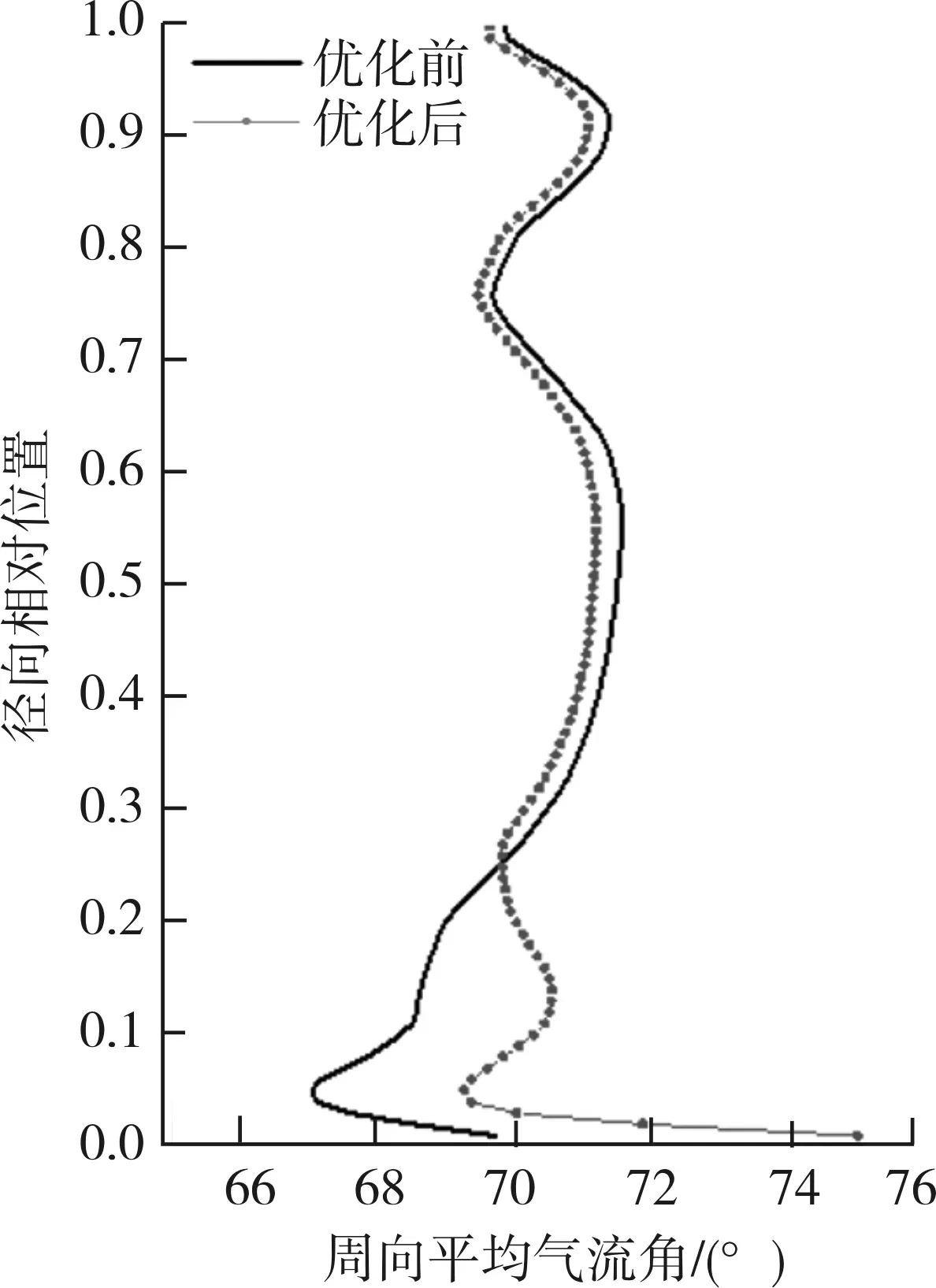
(b) 流动角

4 结 论

本文介绍了一种基于双扰动曲线与改进的Kriging代理模型的非轴对称端壁优化设计系统，将其应用于某型高压透平的第1级，以出口二次流动能系数作为优化目标，对该级动叶轮毂的端壁进行了非轴对称优化设计迭代。最优结果对应的端壁几何特点为：在透平动叶通道前段吸力面侧端壁出现凹陷，降低了横向压力梯度，抑制了低能流体的横向迁移；在接近尾缘处出现端壁凸起，压力梯度向流向偏转，有效降低了出口二次流动能，并提升了流动均匀性，有利于改善下游叶片进口流场与提升透平整体性能。最终该级效率提升了0.11%，证明了本优化系统的有效性。