一种基于中心矩和相关系数阈值的SVD重构算法

何益宏 饶红疆 汪倩文

(五邑大学智能制造学部 广东 江门 529020)

0 引 言

奇异值分解去噪可以有效地分析非线性、非平稳信号，消除信号中的随机噪声[1]。而且重构信号不存在相位偏移和时间延迟[2]，具有良好的稳定性和不变性[3]，在信号处理领域已经得到了广泛应用[4-7]。与其他信号处理技术相比，SVD速度更快且易于实现[8]。

奇异值分解去噪是将一维信号映射到二维Hankel矩阵中，利用有效秩阶次确定信号空间和噪声空间的边界，对信号空间进行降维处理得到去噪后的信号。在矩阵结构确定的前提下，有效秩阶次是决定去噪效果的关键因素。现有的阶次确定方法很多，如奇异值差分谱[9]、奇异值峭度相对变化率[10](SVK)等，但这些方法所确定的阶次存在结果偏大或偏小的问题。例如当原始信号由多个信号分量叠加形成，信号能量弱于噪声能量的部分容易被淹没，对应奇异值谱中幅值较小的奇异值，使用SVK容易将这些奇异值去除，然而这些较小奇异值代表原始信号的某些特征分量，如旋转机械的早期故障微弱特征[11]。这些信号能量较弱的分量丢失会导致去噪后的信号信噪比偏低，而在噪声能量较强的情况下，SVK容易选择过多的奇异值影响SVD去噪的结果。因此，为了提高奇异值分解的去噪性能，研究一种无须选择有效秩阶次的SVD去噪方法具有重要应用价值。

为了解决上述问题，本文提出一种基于中心矩和相关系数阈值的SVD去噪方法，重新优化了Hankel矩阵维数，更小的矩阵维数使奇异值分解速度更快，显著降低计算量，采用相关系数阈值选取有用分量实现信号重构。本文方法无须选择有效秩阶次，避免了阶次选择不当带来的去噪效果不理想的问题。

1 方法设计

1.1 传统SVD去噪方法

传统的SVD去噪方法利用测量信号构建Hankel矩阵，对矩阵进行奇异值分解得到奇异值谱，奇异值以衰减的形式排列，在信号不含噪声的情况下，奇异值谱中只有少数较大的奇异值，而其余的奇异值都为零。因此信号可用少数较大的奇异值重构逼近。对于含噪信号，奇异值谱中所有奇异值都不为零，当信号能量强于噪声时，代表信号的奇异值要大于噪声的奇异值，因此可取前几个较大的奇异值来重构信号，可将其等效为原始信号的有效逼近，而其余的奇异值则代表噪声予以去除。

假设一个含有噪声的数字信号可以表示为：

y(n)=x(n)+e(n)

(1)

式中：y(n)是无噪信号x(n)和噪声e(n)的线性叠加；n表示采样点数。利用测量数据可以构造Hankel矩阵为：

(2)

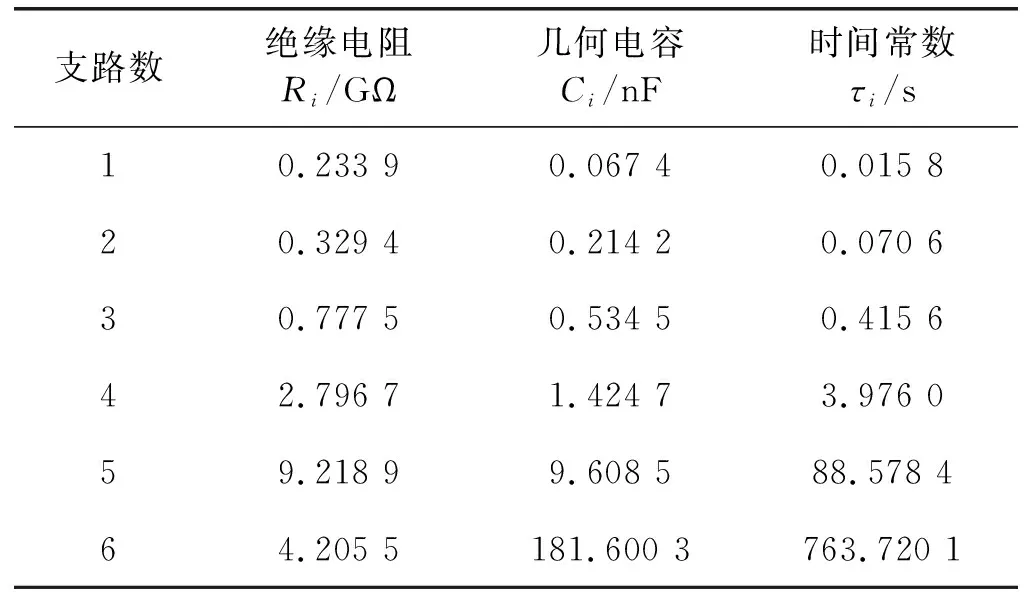
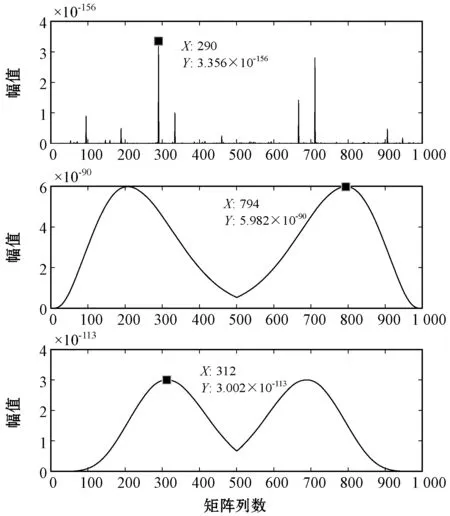
式中：N为信号长度；m为矩阵行数；l为矩阵列数；1

G=USVT

(3)

其中：U∈Rm×m、V∈Rl×l是左右正交奇异矩阵，S=diag(σ1,σ2,…,σr)是只含有不为零的奇异值和零两种元素的对角矩阵，且σ1≥σ2≥…≥σr≥0，r=min(m,l)。若以单个奇异值及相应左右奇异向量表示，G可以表示为r个子矩阵的线性叠加，计算式表示为：

(4)

式中：q是奇异值序列的转折点，前q个奇异值代表有效信号。信号矩阵为：

(5)

对式(5)所得矩阵进行反对角算术平均可得到去噪信号，本文选取SVK作为阶次确定方法。

1.2 改进的SVD去噪方法

传统的SVD去噪方法对信号进行处理时，构建的Hankel矩阵通常采用最大维数法[12-13]，即矩阵列数和行数尽可能最大，且行列数之差最小。文献[14]研究了不同矩阵列数下奇异值的概率分布，发现代表信号的奇异值分布在相对较宽的范围内；而代表噪声的奇异值分布在相对较窄的范围内，而且分布类似于正态。基于此提出用四阶中心矩的四阶根(FRFCM)来确定矩阵列数，去除了探底雷达测量数据噪声。本文在此研究基础上继续计算了一阶、三阶和四阶中心矩的k次幂，可同时得到三个矩阵列数：

(6)

根据式(4)可得：

(7)

(8)

设定一个阈值δ，若相关系数满足：

c(l)={i|CR(i)≥δ}l

(9)

则取对应坐标的分量信号进行线性叠加，得到去噪信号：

(10)

本文认为若某分量属于有效信号，则该分量与第一个分量的相关系数应该大于等于0.1，因此将所有相关系数大于等于0.1的分量叠加起来便可形成去噪后的信号。

1.3 改进方法流程

(1) 利用一阶、三阶和四中心矩的k次幂的峰值坐标确定Hankel矩阵的列数，再根据信号长度等于矩阵行列数之和减1确定矩阵行数，由此得到三个新的Hankel矩阵。

(2) 对每个矩阵进行奇异值分解，根据奇异值分布规律依次取单个奇异值重构信号，得到一系列信号分量，信号分量的个数等于奇异值个数，计算分量之间的相关系数，取相关系数大于等于0.1的分量重构信号。

(3) 根据三个矩阵去噪结果选出最优的去噪信号作为最终结果。

2 实 验

为了验证本文方法的有效性,首先对仿真极化电流信号进行测试与分析,然后再验证对实测极化电流信号的去噪效果。为了定量分析本文方法的去噪性能，以信噪比(SNR)、均方根误差(RMSE)和拟合优度(R2)为评判指标，SNR越大、RMSE越小、R2越接近1则说明去噪效果越好。三种评价指标计算如下：

(11)

2.1 仿真信号叠加实测噪声

为分析本文方法的去噪性能，建立绝缘介质仿真模型，参数取自一台大型电力变压器极化支路辨识结果[16]，具体参数见表1。极化支路总共有6条，极化支路最大时间常数为763.7 s，加压1分钟内第6条支路极化电流变化幅度不大。第5、6条极化支路的极化电阻相对较大，根据欧姆定律可得这两条支路产生的极化电流非常微弱，电流幅值低于1 μA。取测试电压5 kV，仿真时间10 s，采样间隔为0.01 s，信号采样数为1 000，同时利用安捷伦3 4461 A采集现场噪声。

表1 极化支路参数

向仿真极化电流混入1倍实测噪声，实测噪声和含噪极化电流如图1所示。SNR=43.994 9 dB，表明信号的能量强于噪声。从图中可以看出噪声主要分布在曲线变化较为缓慢的阶段，对信号初始阶段几乎没有影响。

图1 实测噪声与含噪极化电流

根据表1参数可知，前3条极化支路的时间常数很小，极化电阻相对也比较小，因此前3条极化支路电流衰减速度较为快速且电流幅值相对较大。第4、5、6条时间常数较大，特别是第6条极化支路时间常数接近1 000 s，极化电阻仅次于第5条极化支路，因此电流衰减非常缓慢，且电流幅值较小容易被噪声干扰，据此可判定图1中含噪极化电流初始阶段主要由前3条极化支路的电流值和噪声叠加形成，中后段主要由第4、5、6条极化支路电流和噪声叠加形成。

图2列出了一阶、三阶和四阶中心矩的8次幂计算结果，由此可确定Hankel矩阵列数分别为290、794和312，矩阵维数分别711×290、794×207和312×689。与传统最大维数法确定的矩阵结构G501×500相比，本文方法确定的矩阵维数更小。从图2可以看出除一阶中心矩以外，其余均是对称结构。

图2 一阶、三阶和四阶中心矩的8次幂确定矩阵列数

表2给出了本文方法和传统SVD的去噪评价指标，结果表明两种方法均能有效去噪，SNR都有一定程度的提高。其中l2=794时SNR最大，相比l=500提升幅度约为52%。从拟合优度和均方根误差看，本文方法去噪信号更加接近理想信号，均方根误差明显比传统SVD去噪信号小，拟合优度更加接近于1，说明去噪信号保留了更多有用成分。综上所述，l2=794的去噪指标最优，将其作为最终的去噪结果。

表2 仿真信号加1倍的外界噪声的去噪指标

为了体现本文方法对不同程度实测噪声的适用性，分别对叠加不同程度噪声的仿真信号进行处理。当仿真信号叠加4倍噪声时，信噪比为16.269 0 dB。由中心矩的8次幂确定Hankel矩阵列数的结果分别为l1=700、l2=232、l3=339，由此确定的Hankel矩阵结构分别为G700×301、G232×769和G339×662。表3给出了去噪信号的评判指标，信噪比反映了去噪信号的能量强度，去噪信号的能量强度越高，信噪比越大。由表3中数据可知本文方法去噪性能优于传统SVD方法，信噪比可提高39%～45%。且本文方法的去噪信号更加接近原始信号，拟合优度非常接近于1。综上所述，l2=232的去噪指标最优，将其作为最终的去噪结果。

表3 仿真信号加4倍的外界噪声的去噪指标

向仿真信号叠加10倍实测噪声时，信噪比为-2.056 8 dB。由中心矩的8次幂确定的Hankel矩阵列数分别为l1=615、l2=709、l3=356，由此确定的Hankel矩阵结构分别为G615×386、G709×292和G356×645。表4给出了去噪信号的评判指标，相比之下，传统SVD方法去噪效果不明显，拟合优度低于0.5，说明去噪信号失真程度严重，而本文方法在Hankel矩阵列数为709时信噪比约为34 dB，为传统方法的2.5倍，拟合优度达到0.9以上，说明去噪信号更加接近原始信号。在噪声比较严重的情况下本文方法仍然有较好的去噪能力和信号保留能力。

表4 仿真信号加10倍的外界噪声的去噪指标

2.2 仿真信号叠加高斯白噪声

为验证在高斯白噪声中本文方法有效，向仿真信号中加入115 dB的高斯白噪声，如图3所示。含噪信号除了初始阶段外全都被噪声覆盖，信噪比为16.633 5 dB。

图3 叠加白噪声的极化电流

图4给出了中心矩的8次幂确定的Hankel矩阵列数分别为l1=241、l2=267、l3=294，由此确定的Hankel矩阵结构分别为G760×241、G267×734和G294×707。所确定Hankel矩阵维数仍然要小于最大维数矩阵。

图4 一阶、三阶和四阶中心矩的8次幂确定矩阵列数

表5给出了两种方法的去噪指标，根据表5中数据可判断l1=241时信噪比最高，比传统SVD方法有明显提高。因此l1=241所构成的矩阵结构是当前几种矩阵结构中去噪效果最好的。

表5 SNR=16.633 5 dB的仿真信号的去噪指标

图5给出了两种方法的去噪信号，从曲线光滑程度对比，两者相差不大，肉眼难以分辨，唯一可见的是去噪信号在初始阶段的幅值有很大差异，这说明截取前k个有效奇异值重构信号保留了信号强度高于噪声的部分，而低于噪声的部分被消除了。

图5 两种方法的去噪信号

当含噪信号的信噪比为-6.463 5 dB时，由中心矩的8次幂确定Hankel矩阵列数分别为l1=241、l2=267、l3=294，由此确定Hankel矩阵结构分别为G760×241、G734×267和G294×707。表6给出了去噪指标，由于噪声能量强于信号能量，重构信号的信噪比最大只有30 dB左右，表明重构信号存在较为严重的有用信息丢失。但相对而言，本文方法的去噪效果更好。

表6 SNR=-6.463 5 dB的仿真信号的去噪指标

综上所述，本文方法在去噪方面的性能优于以有效秩阶次和Hankel矩阵为核心的SVD去噪方法，同时根据中心矩准则优化矩阵结构，降低了计算复杂度。

2.3 实际应用

电力变压器是电网系统中重要的变电设备，而绝缘系统是电力变压器正常运行的基本保障。测量绝缘电阻和吸收比或极化指数能够有效地诊断变压器整体绝缘是否良好。变压器的绝缘电阻可由直流电源电压与极化电流测量值计算得到。极化电流采集原理如图6所示，其中“L”为电源负极，“E”为电源正极，“G”为屏蔽端，主要目的是防止变压器高压侧瓷瓶上的泄露电流进入测量回路。

图6 极化电流测量示意图

测量仪器采用34 461 A，设定PLC积分时间为0.2 s，采样间隔为0.02 s，变压器现场采样极化电流信号如图7所示，信号采样数取613点。现场测量噪声包括环境噪声和仪器的电子噪声。由图可知噪声能量很强，信号趋势无法直接观察出来。一阶中心矩确定的矩阵列数为186,三阶中心矩确定的矩阵列数为214，四阶中心矩确定的矩阵列数为237。由此确定的Hankel矩阵维数分别为186×428、214×400和237×377。

图7 实测极化电流

两种方法的去噪结果如图8所示，由中心矩准则确定的矩阵结构去噪效果最好的是l1=186，其有效信号保留最完整，幅值衰减程度最小。相比之下，传统SVD方法去噪效果不明显，信号带有严重的振荡成分。去噪结果说明在噪声较为严重的情况下，本文方法去噪效果依然优于传统方法。

图8 两种方法去噪结果

3 结 语

传统的SVD方法对测量信号去噪时存在两个问题，一是当噪声能量较小时，有效信号分量中能量小于噪声能量的部分被舍去，重构信号存在能量损失；二是噪声能量强于信号能量时，阶次选择结果偏大使信噪比降低，噪声去除效果不明显。因此传统的SVD方法去噪效果取决于有效秩阶次确定是否准确，这极大地限制了SVD去噪方法的实际应用。为了进一步提升去噪效果，本文提出一种基于中心矩和相关系数阈值的SVD去噪方法。中心矩的峰值可重新确定Hankel矩阵的维数，更小的维数减少了SVD计算量。利用相关系数阈值选取有用信号分量实现去噪，避免了有效秩阶次选择不当带来的问题。