基于ARMA-LSTM组合模型的铁路客流量预测

孙 越 宋晓宇 金莉婷 刘 童

(兰州交通大学电子与信息工程学院 甘肃 兰州 730070)

0 引 言

近年来，由于全球地铁、高铁和磁悬浮列车等方面的高速发展和建设，国内外在客流量预测方面也做了大量的研究与应用。文献[1]提出了一种基于神经网络和起止点矩阵估计的分治方法，实现了对到达各站或离开各站的旅客数量的短期客流预测，并得到了短期内的OD矩阵。文献[2]构建了BP神经网络与灰色预测模型的组合预测模型，弥补了单个模型预测时的不足之处，得到的预测结果均优于传统灰色预测模型。文献[3]研究了ARIMA模型在航空市场需求预测中的应用，对济南至厦门航线的客流进行了分析。文献[4]通过塞尔维亚铁路网实现的月旅客统计的历史数据，得出时间序列具有较强的季节特征自相关。采用了季节性差分自回归滑动平均模型(SARIMA)来拟合并预测，结果表明该方法具有较好的预测性能。文献[5]提出了一种基于深度学习长短期记忆(LSTM)网络结构的地铁站短时客流预测方法。将预测结果与典型时间序列预测算法MLR和BP神经网络进行对比，验证了LSTM网络在地铁站短时客流量预测中具有更高的准确性和很好的适用性。文献[6]用小波变换将处理后的民航客流量信号分解，得到复杂信号的波动特征，再将其输入到BP神经网络中进行预测，效果较好。

如今机器学习发展迅速，研究表明机器学习算法能够很好地处理季节性和非线性的数据[7]。其中有应用于众多领域的人工神经网络ANN(Artificial Neural Networks)模型，它具有很强的自适应和非线性函数逼近能力，不过ANN也存在一定的局限性，比如它在训练过程中易陷入局部极小值，从而出现过拟合和收敛速度过慢的现象[8]。此外，前馈神经网络的预测方法基本是通过前面的部分数据来预测的，它没有记忆和利用历史数据的功能，但对于时间序列而言前后数据之间可能存在密切的依赖关系模式没有被充分利用[9]。循环神经网络RNN(Recurrent Neural Network)中的隐含层具有记忆功能，通过回忆过去来对当前作出判断，但在实际的应用中RNN容易产生梯度消失和梯度爆炸的问题[10]。Hochreiter等[11]在RNN的基础上做了改进后提出了LSTM模型，目前LSTM多用于语音识别、手写识别和自然语言处理等方面。本文提出一种基于LSTM模型和ARMA模型相结合的方法来解决铁路客流量的预测问题，研究结果表明这种组合模型预测方法比单一预测方法的准确性要高。

1 数据集与预处理

1.1 数据预处理

本文所采用的数据是某个区段内客运专线2015年1月至2016年3月的旅客列车梯形密度表。该数据集中包含了每天每个车次在所经过站点的上下车人数，所以需要从中提取出有用的信息，得到一个每天各个站点的客流量数据。对数据表进行数据清洗，主要包括缺失值和异常值的处理。缺失值处理选用了拉格朗日插值法来进行补值，首先从原始数据中确定因变量和自变量，取出缺失值前后3个数据(前后数据中遇到数据不存在或者为空的，直接将数据舍去，将仅有的数据组成一组)，将取出来的6个数据组成一组，然后采用拉格朗日多项式插值公式:

(1)

(2)

式中：x为缺失值对应的下标序号；L(x)为缺失值的插值结果；xi为非缺失值yi的下标序号。对所有的缺失数据逐个做插补操作，直到没有缺失值为止。对于数据集中的异常值主要采取以下两种处理方法：视为缺失值进行插补和取前后数据平均值进行修正。

1.2 特征提取

本文以ZD111-01站点为例，对其数据序列进行特征提取，所用方法为移动平均法，它是根据时间序列逐项推移，依次计算包含一定项数的序列平均数，以此构造出原始序列的特征的向量。类似地，用移动方差算法和移动标准差算法，其具体做法是根据不同的移动窗口M计算出了窗口中M个数据的方差和标准差，然后窗口进行逐一移动，将得到的一系列方差和标准差作为特征序列。

Adaptive-Lasso变量选择方法[12]是1996年被提出的将参数估计与变量选择同时进行的一种正则化方法，这里用该方法从构造的特征序列中筛选识别出关键特征。筛选结果如表1所示，其中移动窗口为7天、10天、14天的移动平均序列(分别用JZ7、JZ10、JZ14表示)和移动标准差序列(分别用BZ7、BZ10、BZ14表示)的影响较高，y代表原始客流量自身，相关度为1。

表1 各特征与原始客流量的相关系数

在对原始序列的分析过程中，采用statsmodels工具包中的seasonal_decompose方法得到了它的周期为7天，如图1所示，这与经验分析也相符，因此将用与原始序列对应的上个7天的所有数据作为一列特征向量。

图1 序列周期图

2 基于ARMA-LSTM的铁路客流量预测模型

2.1 ARMA

ARMA模型的全称是自回归移动平均模型，它和自回归模型(AR模型)、移动平均模型(MA模型)是目前比较常用的拟合平稳时间序列的模型。显然，AR模型和MA模型都是ARMA模型的特例，而且它们也可看作是多元线性回归模型。自回归移动平均模型，简记为ARMA(p,q)模型[13]。模型结构可表示为：

χt=φ0+φ1χt-1+φ2χt-2+…+φpχt-p+
εt-θ1εt-1-θ2εt-2-…-θqεt-q

(3)

式中：φ表示AR的系数；θ表示MA的系数；当在t时刻时，随机变量Xt的取值xt是前p期xt-1,xt-2,…,xt-p和前q期εt-1,εt-2,…,εt-q的多元线性函数;εt是误差项在t时刻的随机干扰，那么可以得出xt主要是受过去p期的序列值和过去q期的误差项的两方面影响。当q=0时，则为AR(p)模型；当p=0时，为MA(q)模型。

所研究的时间序列经过预处理后，如果经过白噪声监测后被判定为平稳非白噪声序列，那么就可以用ARMA模型来对平稳非白噪声序列进行建模：首先计算平稳非白噪声序列的自相关系数(ACF)和偏自相关系数(PACF)；然后进行模型的定阶，由AR(p)、MA(q)和ARMA(p,q)的自相关系数和偏自相关系数的性质来选择合适的模型，识别原则见表2；再估计模型中未知参数的值并检验模型；最后优化模型进行预测。上述模型要求时间序列为平稳序列，而实际上遇到的绝大部分序列是非平稳的，对这种序列可以使用ARIMA模型进行拟合。ARIMA模型的原理是把差分运算与ARMA模型相结合[14]。

表2 ARMA模型识别原则

模型定阶(确定p和q)的方法有很多，常用的一种是通过序列的自相关函数和偏自相关函数来定阶，如果无法得到p和q准确的最优值，可利用赤池信息量准则(Akaike Information Criterion,AIC)或贝叶斯信息准则(Bayesian Information Criterion,BIC)进行定阶[15]。

2.2 LSTM

循环神经网络RNN近些年在时间序列预测分析方面也是一种比较常用的模型，与普通神经网络相比，RNN的隐含层的每次计算结果都与当前输入以及上一次的隐含层结果有关，而普通神经网络的计算结果之间是相互独立的[16-18]。通过这种结构，RNN的计算模型具备了对先前数据的记忆能力。图2为基本的RNN结构，右侧的展开结构更加详细地说明了RNN的原理。其中：x为输入层，o为输出层，s为隐含层，t是指第几次的计算；V、W、U为权重，在计算第t次的隐含层状态时为St=f(UXt+WSt-1)，这样便可以使得当前节点的输入结果与之前结果产生关联。

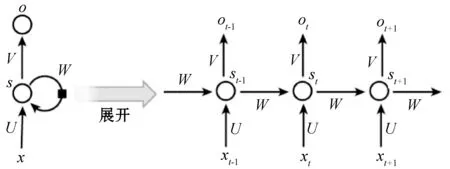
图2 RNN模型结构

如果需要对数据序列进行长期记忆的话，那么RNN模型里面当前隐含层的计算结果要与前n次的计算产生联系。这样会使得计算量呈指数式增长，导致模型在训练时消耗大量时间，而对RNN进行改进后的LSTM模型能够很大程度上避免该问题。LSTM模型的特点就是在RNN的每个神经元内部增加了三类控制记忆单元状态的门结构，分别是输入门(input gate)、遗忘门(forget gate)和输出门(output gate)。输入门决定保存哪些信息到存储单元中。遗忘门决定何时忘记输出结果，从而为输入序列选择最佳的时间间隔。输出门获取所有计算结果并为cell生成输出[19]。典型的LSTM结构如图3所示。

图3 典型的LSTM结构

在本文的客流量预测模型中，输入的时间序列表示为X=(x1,x2,…,xt)，隐藏状态单元表示为H=(h1,h2,…,ht)，输出序列表示Y=(y1,y2,…,yt)。LSTM的计算方法如下：

ht=H(Whyxt+Whhht-1+bh)

(4)

yt=Whyht+by

(5)

上面描述的LSTM结构通过以下计算式实现：

it=σ(Wxixt+Whibt-1+Wcict-1+bi)

(6)

ft=σ(Wxfxt+Whfbt-1+Wcfct-1+bf)

(7)

ct=ft×ct-1+it×tanh(Wxcxt+Whcht-1+bc)

(8)

ot=σ(Wxoxt+Whobt-1+Wcoct-1+bo)

(9)

ht=ottanh(ct)

(10)

式中：σ和tanh表示LSTM模型中特定的激活函数，σ代表式(5)中定义的标准Sigmoid函数,Sigmoid层输出的数值在0到1之间，表示每个部分会有多少量可以通过,“0”表示不会有任何的量通过，“1”则表示允许任意的量通过；i、f、o和c分别表示输入门、遗忘门、输出门和单元激活向量；c需要与隐藏向量h相同；W为权重项；b为各自所对应的偏置项。输入门可以确定什么样的新信息向量x被存放在存储单元状态中，输出门能够使存储单元对输出产生影响。最后，遗忘门决定存储单元记住或忘记其以前的状态[19]。

2.3 ARMA-LSTM模型

本文所研究的客流量问题中需要预测的时间序列显然是一种复杂的非线性的序列，其中包含了不止一种数据特征(线性、非线性和周期性等)，而对于单一预测模型来说就不能很好地捕获数据的各个特征[7]，具有一定的片面性。模型组合的方法能在一定程度上缓解该问题[20-22]，于是本文提出一种基于深度学习方法的ARMA-LSTM模型。该模型主要由三部分组成，第一部分是通过ARMA模型得到预测结果；第二部分是通过LSTM模型得到预测结果；第三部分则是通过优化算法给之前得到的预测结果分配适当的权重系数，再将两种方法的预测结果相加，从而得到最后的预测结果。假设yt(t=1,2,…,n)是实际的时间序列数据，fit(i=1,2)是两种方法的预测结果，wi是第i种预测方法的权重系数，那么组合模型的预测值Yt可以表示为：

(11)

(12)

同时可以得到组合模型预测方法的误差：

(13)

式中：f1t和f2t分别为ARMA和LSTM在t时刻的预测结果；wi(i=1,2)是分配给ARMA和LSTM的权重系数；eit(i=1,2)是ARMA和LSTM在t时刻的误差。这样将ARMA与LSTM的预测结果分别乘以各自对应的权重系数，就可以得到组合模型的预测结果。

3 实验与结果分析

3.1 基于ARMA-LSTM模型的铁路客流量预测

通过之前的数据提取，得到了2015年1月到2016年3月ZD111-01站点的客流量数据，以下实验将用此列数据来完成。经过对数据的分析了解到节假日对客流量的影响很大，因此选取了2015年12月27日至2016年1月20日、2016年2月1日至2016年2月20日、2016年2月24日至2016年3月14日的三段数据分别作为测试集，为了简化表示，在之后内容中简称为1月、2月和3月，这其中主要包含了元旦和春节假期。

用ARMA模型来预测时，首先对数据序列进行平稳性检验(用的方法是单位根检验)和白噪声检验，判定是否为平稳非白噪声序列。然后进行模型识别，再分别通过BIC和AIC信息准则对模型定阶，最后进行预测。在得到的预测结果中选择出误差较小的模型，这里所采用的评价指标是平均绝对百分比误差MAPE(Mean Absolute Percentage Error)。

在进行2015年12月27日至2016年1月20日的客流量预测中，BIC定阶的ARIMA(5,1,5)模型要比其他AIC和BIC分别定阶的ARMA模型和ARIMA模型的误差更低，预测结果如图4所示。

图4 ARIMA(5,1,5)在2016年1月的预测结果

接着搭建LSTM模型，这里主要调用TensorFlow来实现，采用Python 3.5进行程序编写，定义的LSTM网络包含两个隐层，有10个隐层神经元。输入的数据是之前经过特征提取得到的移动窗口为7天、10天、14天的移动平均序列和移动标准差序列，以及与原始序列对应的上一个7天的数据序列。经过反复实验，模型的参数batch_size=1、time_step=7、learning_rate=0.000 6、训练次数为1 000次时预测效果最好。2015年12月27日至2016年1月20日的客流量预测结果如图5所示。

图5 LSTM在2016年1月的预测结果

最后，选择用BP神经网络对权重进行优化，保证组合模型具有最优的拟合效果，进而得出最终的预测结果。经过多次实验，确定BP神经网络参数batch_size=7，nb_epoch=5 000，隐含层神经元为10个，ReLU函数作为激活函数。运算后得到2015年12月27日至2016年1月20日的客流量ARMA-LSTM模型预测结果如图6所示。

图6 ARMA-LSTM在2016年1月的预测结果

通过重复上述步骤，图7-图12给出了各模型分别对2月和3月的预测结果。

图7 ARIMA(5,1,5)在2016年2月的预测结果

图8 LSTM在2016年2月的预测结果

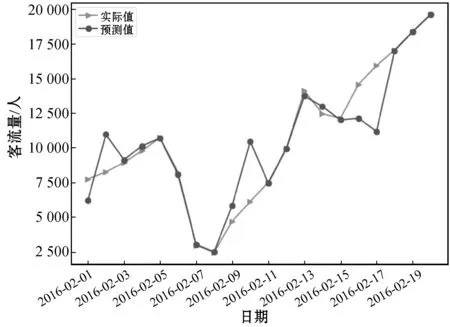
图9 ARMA-LSTM在2016年2月的预测结果

图10 ARMA(4,2)在2016年3月的预测结果

图11 LSTM在2016年3月的预测结果

图12 ARMA-LSTM在2016年3月的预测结果

图7中的2月7日是农历除夕，很明显出现了与实际值较大的误差，这也验证了ARIMA模型在处理这类非线性有剧烈增长和降低的数据时存在的不足。

3.2 评价指标

为了更好地比较不同模型之间的预测效果，本文采用均方根误差(RMSE)和平均绝对百分比误差(MAPE)两种常见的评价指标来量化模型的性能。计算式分别为：

(14)

(15)

式中：N是样本的总数；yi和pi分别是第i个样本数据的真实值和预测值，前者能够很好地反映测量的精度，后者可以衡量一个模型预测结果的好坏。

3.3 模型对比分析

为了更好地分析和对比ARMA-LSTM模型在本次铁路客流量预测中的预测效果，加入了灰色模型GM(1,1)用相同数据进行预测，该模型是使用最广泛的灰色预测模型之一[23]。然后将GM(1,1)与LSTM进行组合，这里同样用BP神经网络对权重进行优化，得到GM-LSTM组合模型的预测结果。下面用RMSE和MAPE两种指标评价五种模型的预测效果，数值越小代表预测效果越好。

表3 五种预测模型的RMSE值

表4 五种预测模型的MAPE值(%)

通过对表3和表4中的数值作比较，可以看出ARMA-LSTM组合模型的预测效果明显优于其他四种模型。三种单一模型中LSTM模型的预测效果较好，但结合图4-图12发现LSTM在一些日期中并没有ARMA拟合得好，在将两模型进行组合后预测效果得到明显提升，因此组合模型ARMA-LSTM不仅在准确性上有了提高，而且在应用场景上吸收了两种模型优势后适用性也高于单一模型。

4 结 语

本文针对铁路客流量问题提出一种基于权重分配的ARMA-LSTM组合模型，利用BP神经网络算法进行优化，将ARMA模型和LSTM模型进行组合来预测铁路的客流量。实验结果分析和比较表明该模型弥补了普通单一模型在实际预测中的不足，提高了客流量预测的准确性以及在该领域中的适用性。而且这种基于神经网络的模型在参数设置和模型训练等方面仍有优化空间，在后续的研究中可继续完善模型以达到更好的预测效果，并且能够使该模型运用到不同的领域中。