基于多层注意力网络的可解释认知追踪方法
2021-12-14孙建文周建鹏刘三女牙何绯娟
孙建文 周建鹏 刘三女牙 何绯娟 唐 云
1(华中师范大学人工智能教育学部 武汉 430079) 2(教育大数据应用技术国家工程实验室(华中师范大学) 武汉 430079) 3(西安交通大学城市学院计算机系 西安 710018) 4(华中师范大学心理学院 武汉 430079)
“利用现代技术加快推动人才培养模式改革,实现规模化教育与个性化培养的有机结合”是《中国教育现代化2035》的战略任务之一.云计算、大数据、人工智能等技术的发展,正推动教育从数字化、网络化向智能化加速跃升,智慧教育成为新一代技术环境下的教育信息化新范式[1],为突破个性化学习技术瓶颈,实现“因材施教”的千年梦想提供了历史机遇.教育情境可计算、学习主体可理解、学习服务可定制是实现个性化学习面临的三大挑战[2],学习主体是教育系统的核心要素,对学习主体的精准洞察是开展“因材施教”的前提.认知追踪(knowledge tracing, KT)作为一种数据驱动的学习主体建模技术,在大规模开放在线课程(massive open online courses, MOOC)、智能导学系统(intelligent tutoring system, ITS)等数字学习平台蓬勃发展、海量学习过程数据爆发式增长等多重效应的加持下,成为近年国内外智能教育领域的研究热点[3-8].
认知追踪的思想源于美国著名心理学家Atkinson[9],1995年被美国卡耐基梅隆大学的Corbett等人[10]引入智能导学系统,并提出贝叶斯认知追踪方法(Bayesian knowledge tracing, BKT),其任务是根据学生过去的答题记录,对学生的知识掌握状态进行建模,目标是预测学生答对下一道题目的概率.2015年,美国斯坦福大学的Piech等人[11]首次将深度神经网络技术用于认知追踪,提出一种基于循环神经网络的深度认知追踪方法(deep knowledge tracing, DKT),在模型预测性能上取得显著提升.DKT的提出顺应了人工智能的技术发展趋势,吸引了多个领域学者的研究兴趣,先后提出DKVMN[12],SKVMN[13],HMN[14],SAKT[15],KQN[16],GKT[17],AKT[18]等一系列新模型.纵观认知追踪的整个发展历程,KT模型从技术上可分为3类[8]:基于概率的模型[10,19]、基于逻辑函数的模型[5,20-21]和基于深度学习的模型(以下称之为深度认知追踪模型)[11-12,15,17,22].深度学习具有强大的拟合非线性函数和特征提取能力,使其适合用于建模复杂的认知过程,相比于概率类和基于逻辑函数的模型往往具有更高的预测性能,尤其是对于海量数据集其优势更加明显[23].但目前大多数深度认知追踪模型均采用具有“黑盒”性质的神经网络技术进行建模,使其预测过程或结果的可解释性较差,难以满足教育领域强调归因分析的需求.
近年来,深度认知追踪模型缺乏可解释性的问题开始受到研究者的重视.其中比较有代表性的工作是将注意力机制应用于认知追踪以提升模型预测结果的可解释性[15,18,22,24].其基本思想在于:学生的历史答题记录反映了当前答题表现,而不同历史答题记录对当前答题的影响是不同的;通过注意力机制使模型学习当前题目与历史答题记录的相关性权重,从而根据相关历史记录的题目信息以及答题情况为模型的预测结果提供一定的解释.但是目前利用注意力机制的认知追踪模型只关注当前题目与历史记录的浅层相关性信息,而忽略了当前题目与历史题目之间的多语义深层关联.由于这些模型仅引入题目-技能关系,只能将模型所学注意力权重归因于题目在技能维度的相似性.然而,能够反映当前题目答题表现的不仅仅是技能相同题目的答题记录,还有其他类型的相似题目,如协同相似[25](即从学生-题目交互数据中挖掘的相似)、模板相似[25]、难度相似[26]等.
题目之间的深层语义关联可从2个层面进行挖掘:1)在哪些语义维度具有关联以及不同语义维度关联强度如何;2)在特定语义维度由哪些元素进行关联以及不同元素的作用如何.“语义”指衡量题目具有关联的方面,如“具有相同技能的题目是有关联的”和“具有相同难度的题目是有关联的”属于不同的语义.“元素”指在特定语义维度关联题目的实体,如题目通过技能进行关联,则技能被称为元素,题目通过学生进行关联,则学生被称为元素.因此,为了建模当前题目与历史答题记录的相关性及其多语义深层关联,提出了一种多层注意力网络,包含记录级注意力、语义级注意力和元素级注意力,如图1所示(相比于其他基于注意力机制的认知追踪模型,增加了语义级和元素级注意力).记录级注意力通过历史题目和当前题目的向量表示计算历史记录的相关性权重,然后按照权重综合历史记录的答题信息对当前答题做预测.语义级注意力能够计算不同语义维度对题目最终向量表示的重要性权重,并根据权重将不同类型的语义信息融合.元素级注意力旨在学习特定语义下不同元素反映题目特征的重要性权重,并按照权重将元素信息聚合到题目上.通过融合多层注意力,不仅可以得到哪些答题记录对当前答题预测具有更高的权重信息,还能获得在计算这些权重时哪些语义信息起到了更大的作用,以及在特定语义下哪些元素更能反映题目的特征.由此,可以结合多层注意力权重分布对模型完整的决策过程进行可视化分析与呈现,详见3.5.1节决策过程分析.
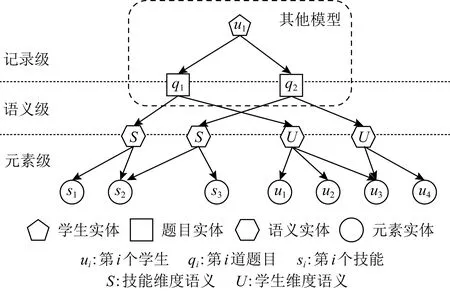
Fig.1 Hierarchical attention structure of HAKT
本文提出一种基于多层注意力网络的认知追踪模型,能够为模型的决策过程和预测结果提供解释.具体地,1)将认知追踪问题域中不同类型实体及其关系表示为异质图,并从中抽取对应不同语义的二部图;2)基于图注意神经网络[27]构建元素级注意力,学习不同二部图中题目节点嵌入;3)利用语义级注意力将多种语义维度的题目嵌入融合成最终题目嵌入;4)基于自注意力机制[28]构建记录级注意力,检索并融合相关历史答题信息,进而预测当前题目的答对概率.
本文贡献主要体现在3个方面:
1)针对当前深度认知追踪模型对预测结果普遍缺乏可解释性或仅通过建模题目之间浅层关系提供解释的问题,提出了一种通过多层注意力网络挖掘题目多语义深层关联信息的方法,能够显著提升模型对预测结果的可解释性.
2)提出了评估认知追踪模型预测结果是否具有可解释性的基本思想,由此设计了提升模型可解释性的损失函数以及预测结果可解释性度量指标.
3)在多个基准数据集上进行了充分实验,并与基于题目嵌入或注意力机制等相关的认知追踪模型进行了比较分析,验证了所提模型在预测性能上的有效性以及预测结果的可解释性.
1 相关工作
1.1 基于深度学习的认知追踪
目前的深度认知追踪模型主要包括DKT[11],DKVMN[12],SAKT[15]及其改进模型.DKT利用循环神经网络来建模学生答题序列,并使用高维连续的隐向量表示认知状态.但是,DKT仅使用题目对应的技能编号作为输入,忽略了其他题目信息.EKT[22],DHKT[29],PEBG[30],GIKT[31],CoKT[25]等模型在DKT的基础上扩展了题目嵌入模块,利用题目文本信息或题目与学生、技能之间的交互信息增强题目表示.DKVMN基于记忆网络建模学生答题序列,利用键、值矩阵分别表示题目的隐藏技能和技能的掌握状态.针对DKVMN无法建模学习过程中长期依赖的问题,SKVMN[13]将LSTM与DKVMN结合,提出HOP-LSTM机制来解决.针对DKVMN仅使用单层记忆网络的不足,HMN[14]引入层次记忆网络分别建模工作记忆和长期记忆,并设计了相应的划分机制和衰减机制.SAKT通过自注意力网络建模学生答题序列,显式地建模当前答题与历史答题记录的相关性.RKT[24]和AKT[18]分别通过引入题目文本信息、题目上下文信息等进一步改进了SAKT,并基于学到的注意力权重对预测结果进行解释性分析.总的来说,当前大多数深度认知追踪模型在预测性能上可取得较好的效果,但可解释性普遍较低.
1.2 可解释深度认知追踪
深度认知追踪模型已然成为认知追踪领域的研究热点,其可解释性研究则方兴未艾.随着可解释性日益成为人工智能领域的研究热点[32-33],认知追踪领域也越来越关注模型的可解释性研究,并形成初步成果.根据解释的对象,可将相关研究分成2类:面向学生认知状态的解释和面向模型预测过程的解释.面向认知状态的解释旨在显式地建模认知状态,即模型内部存在可理解的参数对应每个技能的掌握状态(标量值).由于深度认知追踪模型均使用隐向量表示认知状态,而向量内部的参数难以解释.为使深度认知追踪模型输出可理解的认知状态,目前通常的做法是将其与经典的认知诊断模型结合(如IRT模型)[34-37],其主要方式是将深度模型的输出作为IRT模型的输入,进而利用IRT模型做预测.由于IRT模型的约束,深度模型的输出可以对应IRT模型中可解释的参数(比如可理解的认知状态、学生能力、题目难度等).另外,一些研究者将深度模型已训练好的答题预测模块中的题目嵌入更换为技能嵌入并将对应题目嵌入的部分参数置零,由此将新的输出视为技能的掌握状态值[12,22].面向预测过程的解释旨在解释模型为什么做出这样的预测.目前常用的方法主要是基于注意力机制的解释,包括EKT[22],SAKT[15],RKT[24]和AKT[18]等.其共同点都是通过计算当前答题与历史记录的相关性,进而解释模型在预测时关注哪些记录.然而,这些模型仅建模题目之间的浅层关联信息,忽略了题目之间的多语义深层关联.本文所提模型除了运用自注意力机制建模答题序列,还引入了另外2层注意力机制建模题目之间的多语义深层关联.其优点在于不仅能够挖掘更深层的信息,而且使模型的整个预测过程都具备可解释性.除此之外,也有研究者使用分层相关性传播方法(LRP)对认知追踪模型进行事后可解释分析,计算模型输出与输入的相关性来解释其预测结果[38].
1.3 基于注意力机制的神经网络
由于注意力机制的有效性,其在涉及序列建模的任务中得到广泛应用.其基本思想是:在预测输出时,重点关注输入的相关部分.因此,它在一定程度上为模型提供了可解释性,因为人们可以通过模型所学权重理解模型在进行预测时更关注输入数据的哪些部分.2017年,谷歌团队提出的自注意力机制[28]更是成为目前大规模预训练语言模型的基础.研究者将注意力机制用于图神经网络提出了GAT[27],HAN[39]等图表示学习模型,能够学习不同邻居节点对中心节点的重要性.
2 模 型
本节首先对认知追踪问题进行形式化定义,介绍相关概念的符号表示,然后整体描述模型框架,最后依次介绍模型的各个组成模块以及损失函数.
2.1 问题定义
一方面,认知追踪问题域中的多种实体及其关系组成了异质图G=(E,R),其中E和R分别表示实体和关系集合.实体主要包括学生、题目以及题目的属性标签(即技能、模板等),关系主要为学生-题目和题目-属性等.通过异质图可以挖掘题目之间的多语义深层关联.另一方面,一个学生的答题序列由若干时间步对应的答题记录按照时序关系排列而成,时间步t的答题记录可以表示为xt=(qt,at),qt表示题目编号而at表示答题正确性(0表示答错,1表示答对).在引入题目多语义关联后,认知追踪任务可以被形式化表述为:已知异质图G,当给定学生历史答题序列X={x1,x2,…,xt-1}和当前题目qt,要求预测学生正确回答qt的概率,即P(at=1|G,X,qt).
2.2 整体框架
本文提出基于多层注意力网络的认知追踪模型,包含元素级、语义级和记录级3层注意力.图2展示了模型的整体框架,包括题目嵌入模块、知识检索模块和答题预测模块.
1)题目嵌入模块.首先,从异质图G中抽取不同语义对应的二部图并构建相应的邻接矩阵;然后,通过可学习嵌入层为每个节点生成初始特征向量;接着,基于图注意神经网络分别构建不同语义维度的元素级注意力,学习不同元素的重要性权重,并按照所学权重将邻居元素节点的特征向量聚合到题目节点得到题目嵌入.最后,利用语义级注意力学习不同语义对题目相关性计算的重要性权重,并融合不同语义维度的题目嵌入获得最终题目嵌入.

Fig.2 The overall framework of HAKT
2)知识检索模块.基于自注意力机制构建记录级注意力,显式地建模当前题目与历史记录的相关性,并根据相关性权重融合不同历史答题信息获得学生状态向量.
3)答题预测模块.使用多层感知器(multilayer perception, MLP)建模题目嵌入和学生状态向量的交互过程并预测当前题目的答对概率.
2.3 题目嵌入模块
2.3.1 语义抽取
在异质图中,题目间通过不同元素关联隐含不同的语义信息,例如“题目-技能-题目”表示具有相同技能的题目.从异质图中选取4种关系,每种关系对应一个二部图,每个二部图对应一个邻接矩阵.




2.3.2 元素级注意力

(1)
其中,attnelem表示元素级注意力权重的具体计算过程.首先将中心节点i与其所有邻居j的特征向量各自拼接并通过非线性变换求得权重值;然后通过softmax函数将其归一化.其完整的计算过程为
(2)
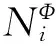

(3)
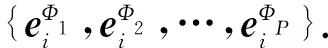
2.3.3 语义级注意力
为了求得最终题目嵌入,需要将不同语义维度的题目嵌入进行融合.对于同一道题目,不同语义的重要性可能是不同的;对于不同的题目,相同语义的重要性也可能是不同的.由此,提出语义级注意力学习不同语义对特定题目的重要性.将元素级注意力所学不同语义维度的题目嵌入作为输入,语义级注意力计算不同语义对题目i的归一化权重:
(4)
其中,attnsem表示语义级注意力权重的具体计算过程.首先将不同语义维度的题目嵌入分别进行非线性变换;然后将变换后的题目嵌入与可学习注意力向量vsem的内积作为权重;最后利用softmax函数将其归一化.语义Φj对题目i的权重的计算过程为
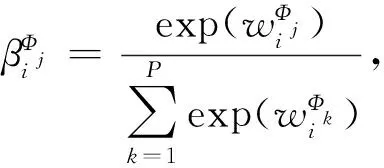

(5)

(6)
2.4 知识检索模块
2.4.1 交互向量生成
通过题目嵌入模块,可以获得任意一道题目i的向量表示ei.对于第t个时间步的题目嵌入,记为et.为了融入答题情况at,将题目嵌入et与相同d维的零向量拼接,获得交互向量xt∈2d:
(7)
相比于循环神经网络,自注意力机制在序列建模中具有更好的灵活性和有效性,且模型内部生成的注意力权重可以为模型预测结果的解释提供基础.因此,与SAKT[15]一样,本文使用自注意力机制建模学生的答题序列.为了将答题交互的相对位置信息编码进模型,定义位置嵌入矩阵P∈l×2d来引入答题序列的位置信息,l为最大序列长度.在加入位置信息后,交互向量表示为表示位置嵌入矩阵中第t行,即第t个时间步的位置嵌入.
2.4.2 记录级注意力

(8)
其中,WQ∈d×d和WK∈2d×d分别是自注意力机制中query和key的映射矩阵.
最后,将历史交互向量按照注意力权重加权求和,得到记录级注意力模块的输出向量ot∈d,即与当前答题相关的学生状态向量:
(9)
其中,WV∈d×d是自注意力机制中value的映射矩阵.
2.4.3 前馈层
为了进一步增强特征的交互能力和模型的拟合能力,将记录级注意力的输出通过point-wise前馈层进行非线性变换.前馈层由2个线性变换组成,中间包含ReLU激活函数,其计算过程为
ht=W(2)ReLU(W(1)ot+b(1))+b(2),
(10)
其中,W(1)∈d×d和W(2)∈d×d为可学习权重矩阵,b(1)∈d和b(2)∈d为可学习偏差向量.
2.5 答题预测模块
预测模块拟合知识检索模块的输出向量ht与题目嵌入et之间的交互函数,预测学生正确回答当前题目的概率.使用多层感知器(MLP)实现:

(11)
(12)
其中,l表示多层感知器的第l∈{1,2,…,L-1}层,W(l)∈d×d和b(l)∈d分别是第l层的权重矩阵和偏差向量,yt是预测概率.
2.6 损失函数及改进策略
尽管在基于注意力机制的认知追踪模型中,相关性权重可以为预测结果的解释提供基础,但是有权重并不意味着一定能够产生易于人们理解的解释过程.例如,如果模型赋予权重较大的几个历史记录的答题情况都是错误(正确)的,但是模型却预测当前题目会答对(答错),那么所学权重就很难对预测结果形成合理的解释.由此本文提出评估预测结果是否具有可解释性的基本思想:模型预测结果与其所关注历史记录的真实答题结果的一致性反映了预测结果的可解释性.

(13)
(14)
(15)

3 实 验
本节首先对实验所用数据集、对比模型和评价指标等进行介绍,然后对各模型预测性能进行对比分析,最后对模型可解释性分别进行定性和定量分析.
3.1 数据集及对比模型介绍
本文在认知追踪领域6个常用的数据集上进行实验,分别是ASSIST09,ASSIST12,ASSIST17,EdNet,Statics2011和Eedi.ASSIST系列数据集是由ASSISTments在线辅导平台收集,其中ASSIST09是目前认知追踪领域最常用的基准数据集;Statics2011收集于某大学静力学课程的辅导系统;EdNet是由在线辅导平台Santa自2017至2019年收集的数据集;Eedi是NeurIPS2020教育数据挖掘挑战赛使用的数据集,由在线教育平台Eedi自2018至2020年收集.
参照现有研究工作,本文对数据集进行预处理:由于ASSIST12,EdNet和Eedi数据集太大,从中随机抽取5 000名学生的数据进行实验[31].对于ASSIST系列数据集,删除脚手架问题关联的记录[40].对于所有数据集,删除技能标签为空的记录[18].对于以技能编号而不是题目编号为输入的模型(即DKT,DKVMN和SAKT),将一道题目的多个技能组合成一个新技能作为输入[40].对于Statics2011,将原题目编号和步骤编号合成新的题目编号作为输入,且对同一题目连续多次作答的情况只保留第一次作答记录.将80%的答题序列作为训练集,其余20%作为测试集[31].最后,从测试集中删除训练集中未出现题目的相关记录.预处理后数据集的统计信息如表1所示.加载数据时,删除长度小于3的答题序列;同时考虑到运行效率问题,将长度超过200的答题序列拆分成多个长度为3~200的序列[18].

Table1 Summary Statistics of Processed Datasets
由于本文所提模型结合题目嵌入和注意力机制,因此为了验证模型在预测性能和可解释性方面的有效性,本文从3方面选取对比模型:经典类模型(DKT[11],DKVMN[12])、题目嵌入类模型(DHKT[29],PEBG[30],GIKT[31])和注意力类模型(SAKT[15],AKT[18]).其中,DKT和DKVMN分别使用循环神经网络和键值记忆网络建模学生序列,是深度认知追踪方向目前最常用的2个基准模型,其均以题目对应的技能编号作为输入.DHKT,PEBG和GIKT是目前预测性能较好的基于题目嵌入的深度认知追踪模型,均以题目-技能关系挖掘题目相似性并学习题目嵌入,再结合DKT或DKVMN做预测.SAKT和AKT均基于自注意力机制,SAKT使用技能编号作为输入,AKT以题目编号作为输入并结合Rasch模型和答题序列的上下文信息学习题目嵌入.SAKT和AKT均只有记录级注意力,本文模型则进一步扩展了语义级注意力和元素级注意力,用于建模多语义深层关联以增强模型可解释性.除了上述对比模型,本文还将输入技能编号的DKT,DKVMN和SAKT分别拓展为输入题目编号的DKT-Q,DKVMN-Q和SAKT-Q.DKT-Q与DKT的不同之处仅在于输入部分由独热编码换成可学习嵌入层,而DKVMN-Q和SAKT-Q在结构上未作改动.
3.2 评价指标
3.2.1 预测性能评价指标
认知追踪任务可以看成是一个二值分类问题,即预测题目回答的正确性(正确或错误).因此,参照绝大多数现有研究工作,本文使用AUC作为衡量模型预测性能的指标.
3.2.2 可解释性评价指标
为了进一步量化模型的可解释性,基于2.6节关于预测结果可解释性评估的基本思想,提出可解释性度量指标:保真度(Fidelity).保真度指可解释模型在输出结果上多大程度上与复杂模型相近,被广泛用于度量机器学习模型的可解释性[33,41].首先定义可解释的预测结果:对于时间步t的预测,若模型预测结果yt与历史答题情况的加权值st的差距小于等于指定阈值θ,则认为该预测结果是可解释的,否则认为不可解释.进一步定义保真度:在所有的预测结果中,可解释的预测结果所占的比例.因此,保真度的计算:
(16)
其中,n表示总预测次数,即测试集中所有序列长度之和.Fidelity越大,表明模型可解释性越好.
3.3 实验设置
对于对比模型:PEBG(1)https://github.com/lyf-1/PEBG和GIKT(2)https://github.com/Rimoku/GIKT的官方代码均从网上获取,其余模型代码根据其论文描述进行复现.其中,PEBG公开代码中在计算题目属性值时使用了测试集数据,存在数据泄露的问题,因此在本文中使用修正后的版本.所有对比模型的超参数或者采用其论文中的最佳设置,或者在验证集(训练集的10%)上进行最优超参数搜索.本文模型HAKT(3)https://github.com/john1226966735/HAKT部分超参数设置为:题目嵌入模块中,题目嵌入维度为128,图注意力网络的注意力头数目为4;知识检索模块中,知识状态向量维度为128,自注意力网络的注意力头数目为8;答题预测模块中,多层感知机层数为2、中间层维度为128;在模型训练阶段,学习率设为0.001,批大小batchsize=32.其余超参数(包括解释性正则化项权衡因子λ)在不同数据集取值不一,均通过超参数搜索确定.另外,2.3.1节中介绍的4种语义(Uc,Uw,S,T)并非全部用于实验.由于数据集特征(如除了ASSIST09和ASSIST12,其他数据集不包含“模板”特征,对应语义T)以及数据分布差异,其对应的最佳语义组合是不同的.通过实验确定每个数据集的最佳语义组合为ASSIST09和ASSIST12:S&T,其余数据集:Uc&Uw&S.
3.4 预测性能分析
表2展示了各个模型在6个数据集上的AUC值(取5次重复实验的均值).分析表2数据可得:
1)对比以技能编号为输入的模型DKT,DKVMN,SAKT及其对应的以题目编号为输入的变体模型DKT-Q,DKVMN-Q,SAKT-Q发现,仅输入题目编号或仅输入技能编号的模型均不能稳定地占有优势.以DKT和DKT-Q为例,在ASSIST17,EdNet和Statics2011这3个数据集上,DKT-Q显著优于DKT,而在其他3个数据集上则相反.其原因是这3个数据集中题目的平均交互次数明显更少(参照表1),表明学生-题目的交互数据很稀疏,从而导致以题目编号为输入的DKT-Q表现更差.
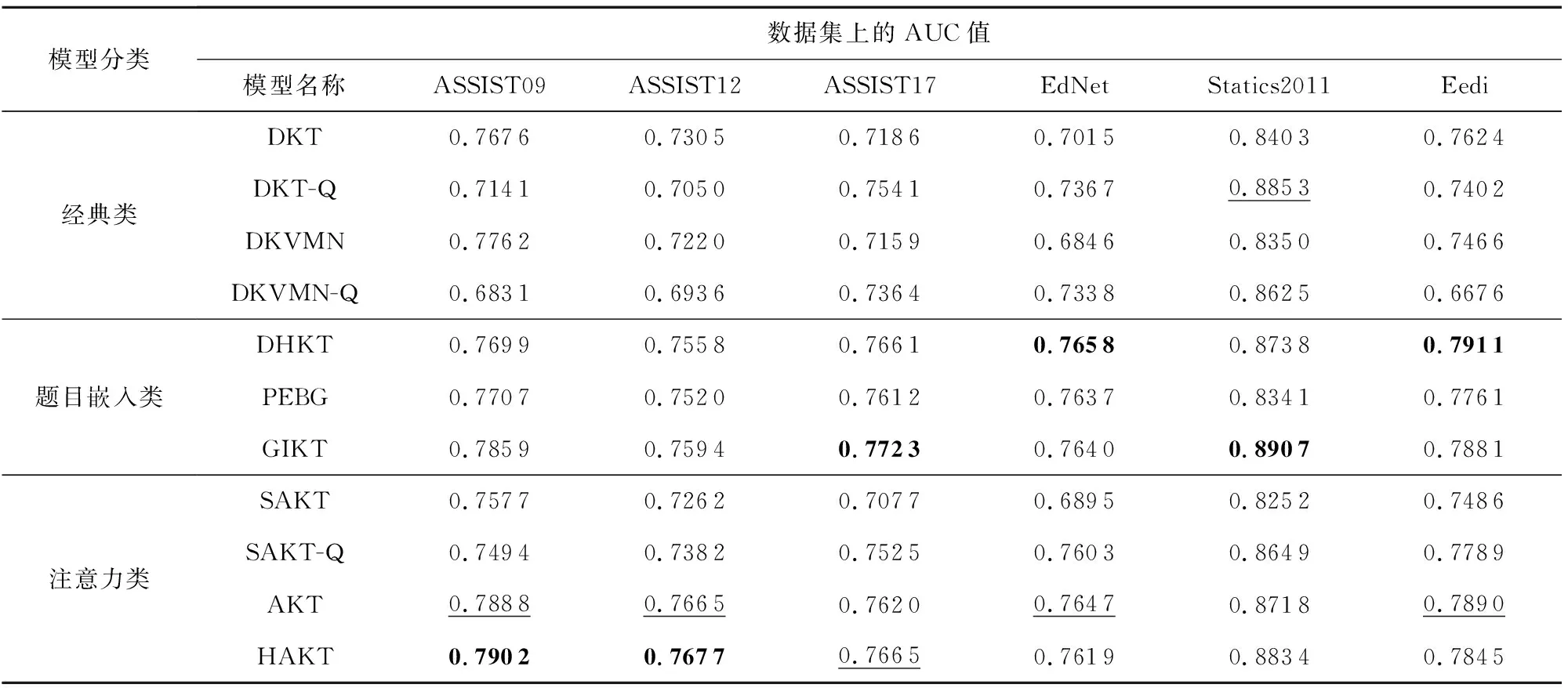
Table 2 Prediction Performance on 6 Datasets
2)通过题目-技能关系同时引入题目和技能信息的模型(即DHKT,PEBG,GIKT,AKT和HAKT)总体上比上述仅使用技能信息或仅使用题目信息的模型预测性能更好.以DKT,DKT-Q和DHKT为例,DHKT在6个数据集上的AUC均值分别比DKT和DKT-Q高3.3个百分点和3.1个百分点.这说明,通过同时引入题目和技能信息,保留题目之间的差异性和相似性,能够使模型的预测更准确.
3)本文模型HAKT在SAKT的基础上扩展题目嵌入模块,相比SAKT取得了显著的提升,并且总体上也略优于其他基于题目嵌入的模型,尤其是DHKT和PEBG.这表明,相比于后者单纯引入技能维度关联,HAKT通过引入题目的多语义关联使得模型可以更准确地挖掘题目之间的语义关系,从而学到更优的题目嵌入.在ASSIST09和ASSIST12数据集上HAKT表现最佳,其他数据集上与最优模型的差距约0.5个百分点,这说明HAKT在提升模型可解释性的同时也具有较高的预测性能.
4)本文实现的SAKT在所有数据集上预测性能均低于DKT,这一结果与AKT[18]一文中的结果一致.其可能的原因是,一方面认知追踪领域的数据量较小,另一方面该领域数据集中相似题目往往依次出现,使得题目之间的依赖距离较短.因此,自注意力机制无法发挥其特有的优势.同样,相比于DHKT和GIKT主要基于循环神经网络,HAKT完全基于自注意力机制,这可能也是HAKT在部分数据集预测性能略低于两者的原因.
3.5 可解释性分析
3.5.1 决策过程分析
HAKT能够通过其内部计算的注意力权重分布对预测过程和结果提供可解释性分析.相比基于单层注意力机制的模型(如EKT,RKT,AKT等),HAKT整合多层注意力的权重分布能够生成更精确、完整的模型决策过程.具体地,HAKT不仅能检索出哪些历史题目与当前题目关联,还能得到它们是如何进行关联的.通过案例来分析HAKT的可解释性.
从测试集中随机选择一名学生(记为u1),图3对模型预测学生回答第20道题目(即q20)时生成的多层注意力权重分布以及题目之间的关联图进行可视化.为了方便展示,仅呈现权重较大的部分历史题目(即q18和q19)及权重较大的部分相关语义(S表示技能维度,Uc表示学生维度)和元素(如s1和u1等).分析图3得:
1)根据记录级注意力权重分布,模型在预测当前答题时q18和q19被赋予最大的权重且其真实答题情况均为“正确”;模型预测当前答题正确的概率为0.75(即答对概率较高).这说明模型当前预测结果与权重较大的历史记录的答题情况一致,即模型能从历史记录中找到与当前答题相关的记录,并综合历史答题情况对当前答题做预测.
2)尽管通过记录级注意力能够检索出哪些历史记录对当前答题影响更大,但是这些历史题目与当前题目是如何进行关联的无法得知.进一步,通过语义级注意力权重分布可知,对于相关历史题目q19,语义Uc的权重较大.这说明它们的关联主要源于其具有相似的答题交互记录.那么与哪些学生的交互体现了它们的关联呢?通过元素级注意力权重分布可知,学生u3和u4的权重较大,这说明由于这些学生均答对了q19和q20,使得模型认为这2道题目具有关联.
3)由此,综合3层注意力可得模型预测当前答题的决策过程,可由图3中实线呈现,同时实线部分也表明了历史记录与当前题目的语义关联:由于当前题目与历史题目q19具有相似的交互记录且与q18具有相同的技能,且q18和q19均回答正确,因此模型预测当前题目答对的概率较高.

Fig.3 Visualization of model’s decision process
此外,为了验证模型在决策可解释性方面的可靠性,本文进一步探究:在所有答题预测中,权重较大的历史记录与当前题目存在语义关联的比例有多大?首先,定义题目的语义关联性:若2道题目至少在一个语义层面具有相同的元素,则它们具有语义关联性,即关联性标签为1,否则关联性标签为0.然后,定义单次预测中较大权重历史记录与当前题目是否具有相关性:若权重最大的前k个历史记录中至少有一个与当前预测题目具有语义关联性,则当次预测命中相关题目,记为1,否则为0;最后,计算命中相关题目的预测数占所有预测数的比例(命中率).以ASSIST09数据集为例,所选语义组合为S&T,即技能维度和模板维度.取k=3,命中率为90.5%(若随机选择3个历史记录则命中率为43.7%),即在90%以上的预测中,模型赋予权重最大的3个历史记录,至少有1个历史记录与当前预测题目有显式的语义关联(即有相同技能或相同模板).因此,HAKT不仅能够捕获题目之间的相关性,并且对模型决策过程的解释具有较高的可靠性.
3.5.2 一致性分析
为了进一步验证案例分析中的观察(即:模型当前的预测结果与相关性权重较大的历史记录的答题情况具有更高的一致性),对模型预测值和历史相关题目答题结果进行一致性分析.参考EKT[22]:
1)对于某个学生在某一时间步的预测,首先计算历史答题记录对应的注意力权重,然后将这些答题记录按照注意力权重大小等分成高、中、低3组,最后将每一组的答题得分(正确为1,错误为0)各自按照注意力权重进行加权求和.
2)对于每一组,计算该学生所有时间步对应的加权求和值与模型预测值之间的根均方差(表示在考虑当前题目的情况下历史答题情况与当前预测值的一致性).
3)将所有学生对应的根均方差以散点图和盒式图的形式展示出来,如图4所示.从图4中可以看出,在所有数据集中,高注意力权重组对应的根均方差均值明显小于其他组(即其答题情况与预测结果的一致性最好),且中注意力权重组对应的根均方差均值同样明显小于低注意力权重组.

Fig.4 Analysis of the consistency between historical answers and predicted probability

Fig.5 Variation of fidelity of each model with interpretability threshold
进一步,采用双样本T检验对3组的差距进行显著性分析.对高、中组和中、低组分别进行检验分析得p值均远远小于显著性基准值0.01,说明3组的差距是显著的.这一发现表明,从统计意义上来说相关权重更大的历史答题与模型当前的预测结果具有更高的一致性.这说明不同历史记录对当前答题预测的影响是不一样的,所以引入注意力机制能有效利用这一规律,从而提升模型的预测性能和可解释性.
3.5.3 可解释性度量
为了进一步评估和对比各模型对于预测结果的可解释性,在所有数据集上实验并绘制模型保真度随可解释性阈值θ的变化曲线,如图5所示.其中,HAKT(λ)表示解释性正则化项中权衡因子为λ的模型,HAKT(0)则表示无解释性正则化项的版本;SAKT和AKT是对比模型.从图5中可看到:
1)在其中4个数据集上,HAKT(0)的保真度均高于SAKT和AKT,说明在不加解释性正则化项的情况下,本文所提模型通过建模题目的多语义关联一定程度上提升了模型的可解释性.
2)当加入解释性正则化项且权衡因子λ增大时,保真度也随之明显上升,这说明引入解释性正则化项显著提升了模型对预测结果的可解释性.注意到AKT的保真度总体上较低,潜在原因是AKT相比SAKT和HAKT具有更深的自注意力层和更复杂的结构,由此降低了可解释性.
为了进一步观察HAKT中权衡因子λ如何影响预测性能和可解释性,将不同λ值(固定θ=0.20)对应的AUC和保真度以散点图的形式呈现(如图6所示).从图6中可以观察到:总体上看,随着λ增大,AUC减小而保真度增大.以ASSIST09数据集为例,当λ从0增大到0.3时,AUC从79.02%降至78.81%(下降0.2个百分点),而保真度从89.71%升至95.52%(上升5.71个百分点).这说明模型可解释性与预测性能难以同时提升,两者需要平衡.HAKT可以通过改变权衡因子调控模型的预测性能和可解释性,在模型预测性能略有下降的情况下,显著提升其可解释性.
在本文所用数据集中,同时考虑模型预测性能和可解释性的情况下,权衡因子λ的较优取值处于0.05~0.2之间,此时预测性能略有下降而保真度有较明显的提升.
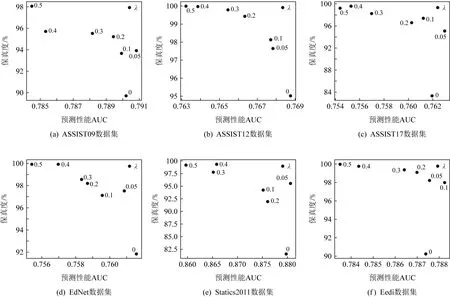
Fig.6 The impact of trade-off factor λ on predictive performance and interpretability
4 总 结
针对现有深度认知追踪模型对预测结果普遍缺乏可解释性或者部分模型仅建模题目之间浅层关系的不足,本文提出一种基于多层注意力网络挖掘题目多语义关联的认知追踪模型,进一步提升了模型的预测性能和可解释性.在损失函数中引入解释性正则化项及权衡因子,在预测性能略有下降的情况下明显提升了其可解释性.设计了评估模型预测结果可解释性的量化指标.在6个领域基准数据集上进行了预测性能对比实验和可解释性分析,验证了本文所提模型同时具有较高的预测性能和可解释性.
深度认知追踪是当前国内外智能教育领域的研究热点之一,可有效支撑学习者建模、学习路径规划、学习资源适配等个性化服务.未来,人工智能技术的持续、快速发展,不断为深度认知追踪方法创新提供新的动能.比如旨在突破人工智能非线性瓶颈的下一代人工智能——精准智能[42],为处理复杂对象可解释性、泛化性与可复现性等难题提供了可能,也为进一步改进深度认知追踪技术带来新的机遇.
作者贡献声明:孙建文提出研究问题,设计研究框架,撰写和修改论文,管理研究过程;周建鹏主要负责数据处理、形式化建模、实验设计分析与论文起草;刘三女牙主要提供研究思路与方法指导;何绯娟主要提供研究经费支持,完善研究思路与框架,指导论文修改等;唐云主要提供文献调研、认知建模理论与实验结果分析等指导性支持.
